Article contents
Improved algebraic fibrings
Published online by Cambridge University Press: 13 September 2024
Abstract
We show that a virtually residually finite rationally solvable (RFRS) group 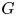 $G$ of type
$G$ of type 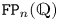 $\mathtt {FP}_n(\mathbb {Q})$ virtually algebraically fibres with kernel of type
$\mathtt {FP}_n(\mathbb {Q})$ virtually algebraically fibres with kernel of type 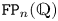 $\mathtt {FP}_n(\mathbb {Q})$ if and only if the first
$\mathtt {FP}_n(\mathbb {Q})$ if and only if the first 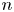 $n$
$n$ 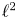 $\ell ^2$-Betti numbers of
$\ell ^2$-Betti numbers of 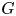 $G$ vanish, that is,
$G$ vanish, that is, 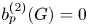 $b_p^{(2)}(G) = 0$ for
$b_p^{(2)}(G) = 0$ for 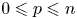 $0 \leqslant p \leqslant n$. This confirms a conjecture of Kielak. We also offer a variant of this result over other fields, in particular in positive characteristic. As an application of the main result, we show that amenable virtually RFRS groups of type
$0 \leqslant p \leqslant n$. This confirms a conjecture of Kielak. We also offer a variant of this result over other fields, in particular in positive characteristic. As an application of the main result, we show that amenable virtually RFRS groups of type 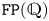 $\mathtt {FP}(\mathbb {Q})$ are virtually Abelian. It then follows that if
$\mathtt {FP}(\mathbb {Q})$ are virtually Abelian. It then follows that if 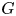 $G$ is a virtually RFRS group of type
$G$ is a virtually RFRS group of type 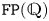 $\mathtt {FP}(\mathbb {Q})$ such that
$\mathtt {FP}(\mathbb {Q})$ such that 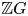 $\mathbb {Z} G$ is Noetherian, then
$\mathbb {Z} G$ is Noetherian, then 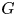 $G$ is virtually Abelian. This confirms a conjecture of Baer for the class of virtually RFRS groups of type
$G$ is virtually Abelian. This confirms a conjecture of Baer for the class of virtually RFRS groups of type 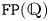 $\mathtt {FP}(\mathbb {Q})$, which includes (for instance) the class of virtually compact special groups.
$\mathtt {FP}(\mathbb {Q})$, which includes (for instance) the class of virtually compact special groups.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2024. The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence
References
- 2
- Cited by


