Let $G$ be a split semisimple group over a global function field $K$. Given a cuspidal automorphic representation $\Pi$ of $G$ satisfying a technical hypothesis, we prove that for almost all primes $\ell$, there is a cyclic base change lifting of $\Pi$ along any $\mathbb {Z}/\ell \mathbb {Z}$-extension of $K$. Our proof does not rely on any trace formulas; instead it is based on using modularity lifting theorems, together with a Smith theory argument, to obtain base change for residual representations. As an application, we also prove that for any split semisimple group $G$ over a local function field $F$, and almost all primes $\ell$, any irreducible admissible representation of $G(F)$ admits a base change along any $\mathbb {Z}/\ell \mathbb {Z}$-extension of $F$. Finally, we characterize local base change more explicitly for a class of toral representations considered in work of Chan and Oi.

We use sheaves of spectra to quantize a Hamiltonian 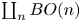$\coprod _n BO(n)$-action on 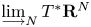$\varinjlim _{N}T^*\mathbf {R}^N$ that naturally arises from Bott periodicity. We employ the category of correspondences developed by Gaitsgory and Rozenblyum [A study in derived algebraic geometry, vol. I. Correspondences and duality, Mathematical Surveys and Monographs, vol. 221 (American Mathematical Society, 2017)] to give an enrichment of stratified Morse theory by the 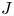$J$-homomorphism. This provides a key step in the work of Jin [Microlocal sheaf categories and the 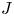$J$-homomorphism, Preprint (2020), arXiv:2004.14270v4] on the proof of a claim of Jin and Treumann [Brane structures in microlocal sheaf theory, J. Topol. 17 (2024), e12325]: the classifying map of the local system of brane structures on an (immersed) exact Lagrangian submanifold 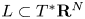$L\subset T^*\mathbf {R}^N$ is given by the composition of the stable Gauss map 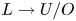$L\rightarrow U/O$ and the delooping of the 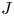$J$-homomorphism 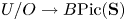$U/O\rightarrow B\mathrm {Pic}(\mathbf {S})$. We put special emphasis on the functoriality and (symmetric) monoidal structures of the categories involved and, as a byproduct, we produce several concrete constructions of (commutative) algebra/module objects and (right-lax) morphisms between them in the (symmetric) monoidal 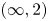$(\infty, 2)$-category of correspondences, generalizing the construction out of Segal objects of Gaitsgory and Rozenblyum, which might be of independent interest.

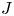We describe the $J$-invariant of a semisimple algebraic group $G$ over a generic splitting field of a Tits algebra of $G$ in terms of the $J$-invariant over the base field. As a consequence we prove a 10-year-old conjecture of Quéguiner-Mathieu, Semenov, and Zainoulline on the $J$-invariant of groups of type $\mathrm {D}_n$. In the case of type $\mathrm {D}_n$ we also provide explicit formulas for the first component and in some cases for the second component of the $J$-invariant.

We investigate the Gross–Prasad conjecture and its refinement for the Bessel periods in the case of $(\mathrm {SO}(5), \mathrm {SO}(2))$. In particular, by combining several theta correspondences, we prove the Ichino–Ikeda-type formula for any tempered irreducible cuspidal automorphic representation. As a corollary of our formula, we prove an explicit formula relating certain weighted averages of Fourier coefficients of holomorphic Siegel cusp forms of degree two, which are Hecke eigenforms, to central special values of $L$-functions. The formula is regarded as a natural generalization of the Böcherer conjecture to the non-trivial toroidal character case.

We show that a virtually residually finite rationally solvable (RFRS) group $G$ of type $\mathtt {FP}_n(\mathbb {Q})$ virtually algebraically fibres with kernel of type $\mathtt {FP}_n(\mathbb {Q})$ if and only if the first $n$ $\ell ^2$-Betti numbers of $G$ vanish, that is, $b_p^{(2)}(G) = 0$ for $0 \leqslant p \leqslant n$. This confirms a conjecture of Kielak. We also offer a variant of this result over other fields, in particular in positive characteristic. As an application of the main result, we show that amenable virtually RFRS groups of type $\mathtt {FP}(\mathbb {Q})$ are virtually Abelian. It then follows that if $G$ is a virtually RFRS group of type $\mathtt {FP}(\mathbb {Q})$ such that $\mathbb {Z} G$ is Noetherian, then $G$ is virtually Abelian. This confirms a conjecture of Baer for the class of virtually RFRS groups of type $\mathtt {FP}(\mathbb {Q})$, which includes (for instance) the class of virtually compact special groups.

We categorify the inclusion–exclusion principle for partially ordered topological spaces and schemes to a filtration on the derived category of sheaves. As a consequence, we obtain functorial spectral sequences that generalize the two spectral sequences of a stratified space and certain Vassiliev-type spectral sequences; we also obtain Euler characteristic analogs in the Grothendieck ring of varieties. As an application, we give an algebro-geometric proof of Vakil and Wood's homological stability conjecture for the space of smooth hypersurface sections of a smooth projective variety. In characteristic zero this conjecture was previously established by Aumonier via topological methods.