Le principe de Hasse pour les espaces homogènes : réduction au cas des stabilisateurs finis

Abstract

Nous montrons, pour une grande famille de propriétés des espaces homogènes, qu’une telle propriété vaut pour tout espace homogène d’un groupe linéaire connexe dès qu’elle vaut pour les espaces homogènes de 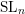$\text{SL}_{n}$ à stabilisateur fini. Nous réduisons notamment à ce cas particulier la vérification d’une importante conjecture de Colliot-Thélène sur l’obstruction de Brauer–Manin au principe de Hasse et à l’approximation faible. Des travaux récents de Harpaz et Wittenberg montrent que le résultat principal s’applique également à la conjecture analogue (dite conjecture (E)) pour les zéro-cycles.

For a large family of properties of homogeneous spaces, we prove that such a property holds for all homogeneous spaces of connected linear algebraic groups as soon as it holds for homogeneous spaces of 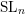$\text{SL}_{n}$ with finite stabilisers. As an example, we reduce to this particular case an important conjecture by Colliot-Thélène about the Brauer–Manin obstruction to the Hasse principle and to weak approximation. A recent work by Harpaz and Wittenberg proves that the main result also applies to the analogous conjecture (known as conjecture (E)) for zero-cycles on homogeneous spaces.

1 Introduction

Soit $k$ un corps de nombres et considérons une famille de $k$ -variétés lisses et géométriquement intègres. On dit qu’une telle famille vérifie le principe de Hasse, ou principe local–global, si pour toute variété $X$ dans cette famille on a l’implication suivante :

(PH) $$\begin{eqnarray}X(k_{v})\neq \emptyset ,\quad \forall \,v\in \unicode[STIX]{x1D6FA}_{k}\,\Rightarrow \,X(k)\neq \emptyset ,\end{eqnarray}$$

où $\unicode[STIX]{x1D6FA}_{k}$ désigne l’ensemble des places de $k$ et $k_{v}$ désigne le complété correspondant à la place $v$ . La question de la vérification du principe local–global est déjà classique en géométrie arithmétique et remonte aux résultats de Hasse lui-même sur les quadriques au début du XX^e siècle.

Une question analogue à celle du principe de Hasse est celle de l’approximation faible, laquelle s’intéresse à la densité des $k$ -points d’une variété $X$ dans le produit des points dans ses complétés, i.e.

(AF) $$\begin{eqnarray}X(k)\neq \emptyset \,\Rightarrow \,\overline{X(k)}=\mathop{\prod }_{v\in \unicode[STIX]{x1D6FA}_{k}}X(k_{v}).\end{eqnarray}$$

Soit maintenant $G$ un $k$ -groupe algébrique linéaire connexe. On rappelle qu’un ( $k$ -) espace homogène de $G$ est une $k$ -variété $X$ munie d’une $k$ -action de $G$ qui est transitive au niveau des $\bar{k}$ -points, où $\bar{k}$ désigne une clôture algébrique de $k$ . Dans ce texte, on s’intéresse aux propriétés arithmétiques décrites ci-dessus pour de telles variétés.

Les questions sur la validité du principe de Hasse et de l’approximation faible pour les espaces homogènes des groupes linéaires ont été étudiées notamment par Sansuc et Borovoi, avec par exemple la vérification des deux propiétés pour les espaces homogènes de groupes semi-simples et simplement connexes à stabilisateur semi-simple ou unipotent (cf. [Bor93]). On sait cependant que ce principe n’est pas vérifié en général et c’est déjà le cas pour les espaces principaux homogènes de tores, ou de groupes semi-simples à partir du moment où l’on ne les suppose plus simplement connexes (cf. [San81]). En revanche, on peut expliquer ces contre-exemples avec l’obstruction de Brauer–Manin. Dans ce sens, et généralisant les travaux de Sansuc, Borovoi a établi que l’obstruction de Brauer–Manin est la seule obstruction au principe de Hasse et à l’approximation faible pour tout espace homogène $X$ de $G$ à stabilisateur connexe, ou encore à stabilisateur abélien si l’on suppose $G$ simplement connexe (cf. [Bor96]). Autrement dit, on a les propriétés

(BMPH) $$\begin{eqnarray}\bigg[\mathop{\prod }_{v\in \unicode[STIX]{x1D6FA}_{k}}X(k_{v})\bigg]^{\text{Br}_{\text{nr}}}\neq \emptyset \Rightarrow X(k)\neq \emptyset\end{eqnarray}$$

et

(BMAF) $$\begin{eqnarray}X(k)\neq \emptyset \,\Rightarrow \,\overline{X(k)}=\bigg[\mathop{\prod }_{v\in \unicode[STIX]{x1D6FA}_{k}}X(k_{v})\bigg]^{\text{Br}_{\text{nr}}}.\end{eqnarray}$$

Pour la définition de l’ensemble de Brauer–Manin $[\prod _{v\in \unicode[STIX]{x1D6FA}_{k}}X(k_{v})]^{\text{Br}_{\text{nr}}}\subset \prod _{v\in \unicode[STIX]{x1D6FA}_{k}}X(k_{v})$ , voir la section 2.1.

La question pour les stabilisateurs non connexes reste cependant ouverte, notamment pour les stabilisateurs finis : à propos du principe de Hasse, le cas abélien a été traité par Borovoi, les auteurs ont obtenus quelques résultats particuliers (cf. [Dem10, LA14]), et récemment Harpaz et Wittenberg ont obtenus une avancée substantielle dans le cas des stabilisateurs hyper-résolubles (voir [HW18], théorème B). Il est important de remarquer cependant que, d’après une conjecture de Colliot-Thélène sur les variétés rationnellement connexes, le même résultat est attendu dans le cas général.

Des énoncés similaires, ouverts eux aussi, peuvent être donnés pour les zéro-cycles de degré 1. On peut notamment se demander si l’existence d’un zéro-cycle de degré 1 sur chaque complété $k_{v}$ implique l’existence d’un zéro-cycle de degré 1 sur $k$ , modulo une obstruction de Brauer–Manin. De façon plus précise, on conjecture l’exactitude de la suite suivante :

(E) $$\begin{eqnarray}\mathop{\varprojlim }\nolimits_{n}\text{CH}\,_{0}(X^{c})/n\rightarrow \mathop{\varprojlim }\nolimits_{n}\mathop{\prod }_{v\in \unicode[STIX]{x1D6FA}_{k}}\text{CH}\,_{0}(X^{c}\times _{k}k_{v})/n\rightarrow \text{Hom}(\text{Br}\,X^{c},\mathbb{Q}/\mathbb{Z}),\end{eqnarray}$$

où $X^{c}$ est une compactification lisse de $X$ et $\text{CH}\,_{0}$ désigne le groupe des zéro-cycles modulo équivalence rationnelle (si $v$ est une place infinie, on remplace en fait $\text{CH}\,_{0}$ par une version modifiée) et la flèche à droite est induite par l’accouplement de Brauer–Manin. Ces énoncés sont connus sous le nom de ‘Conjecture (E)’ ; cf. par exemple [Wit12, § 1.1].

Le but de cet article est de montrer que l’on peut réduire ces questions générales au cas des espaces homogènes de $\text{SL}_{n,k}$ à stabilisateur fini. Il s’agit donc de suivre la démarche entreprise par le deuxième auteur dans [LA17], qui traitait de la propriété (BMAF). Notons que le passage de (BMAF) à (BMPH) ou (E) est délicat car on perd justement l’hypothèse sur l’existence de points rationnels. Il est important de noter que le fait d’enlever l’hypothèse d’existence d’un point rationnel est réellement nécessaire pour obtenir les nouvelles applications. On obtient ainsi par exemple la conséquence suivante du résultat principal de ce texte.

Théorème 1.1 (Conséquence du théorème 5.2). Si l’obstruction de Brauer–Manin est la seule obstruction au principe de Hasse (BMPH) et à l’approximation faible (BMAF) pour tout espace homogène de $\text{SL}_{n,k}$ à stabilisateur fini, alors il en va de même pour tout espace homogène $X$ d’un groupe linéaire connexe.

Notons qu’un travail récent [HW18] de Harpaz et Wittenberg démontre la conjecture (E) pour les espaces homogènes de groupes linéaires connexes en utilisant le théorème 5.2 pour montrer qu’essentiellement l’exactitude de la suite (E) pour les espaces homogènes se réduit au cas des espaces homogènes de $\text{SL}_{n,k}$ à stabilisateurs finis.

On remarquera que, à la différence du résultat principal de [LA17], qui correspond au même énoncé que le théorème 5.2, mais seulement avec la propriété (BMAF), on n’a pas un énoncé analogue avec seulement la propriété (BMPH). En effet, on a besoin d’un minimum de propriétés d’approximation pour que notre preuve, qui utilise la méthode des fibrations, fonctionne. Le mieux que l’on puisse faire pour l’instant est de remplacer (BMAF) par ‘approximation réelle’ dans l’énoncé ci-dessus, ce qui est une hypothèse plus faible, mais non triviale tout de même ; cf. le début de la section 5.

La preuve de ce résultat s’inspire de celle dans [LA17], mais il est nécessaire de généraliser plusieurs outils présents dans celle-ci. Le point crucial est que dans un espace homogène ayant un point rationnel, le stabilisateur de ce point est un $k$ -groupe, alors qu’en général, on dispose seulement d’une $k$ -gerbe. La nouveauté principale de ce texte est donc de donner un sens à des phrases telles que ‘plonger une $k$ -gerbe dans $\text{SL}_{n,k}$ ’ ou ‘faire agir une $k$ -gerbe sur un tore’.

Le plan du texte est le suivant. Dans la section 2, on donne un rappel succinct sur l’obstruction de Brauer–Manin et un rappel plus complet sur la 2-cohomologie non abélienne. On définit notamment, pour $K$ un corps parfait, les notions de $K$ -lien et $K$ -gerbe de plusieurs façons déjà classiques mais qui, à notre connaissance, n’ont jamais été toutes comparées en un seul texte dans la littérature. On conclut cette section en rappelant le lien entre la 2-cohomologie et les espaces homogènes sous ces différents points de vue. La section 3 est consacrée au ‘plongement d’une $K$ -gerbe dans $\text{SL}_{n,K}$ ’. On démontre au passage une généralisation du fameux ‘Lemme sans nom’ (Corollaire 3.5), qui affirme que deux espaces homogènes de $\text{SL}_{n,K}$ ou de $\text{GL}_{n,K}$ ayant la même $K$ -gerbe associée sont $K$ -stablement birationnels. La section 4 s’occupe de l’action d’une $K$ -gerbe sur un tore. On reprend ici ce qui a été fait dans [LA17, § 3] autour du lemme d’Ono pour l’étendre à ce nouveau cadre. Enfin, la section 5 est consacrée à l’énoncé et la preuve du théorème principal.

2 Préliminaires

Dans tout le texte, on désigne par $K$ un corps parfait, $\bar{K}$ une clôture algébrique et $\unicode[STIX]{x1D6E4}_{K}$ le groupe de Galois absolu $\text{Gal}(\bar{K}/K)$ . On réserve la notation $k$ pour un corps de nombres. On note alors $\unicode[STIX]{x1D6FA}_{k}$ l’ensemble des places de $k$ et, pour $v\in \unicode[STIX]{x1D6FA}_{k}$ , on note $k_{v}$ le complété correspondant.

Une $K$ -variété algébrique $X$ sera toujours supposée lisse et géométriquement intègre. Pour $A/K$ une $K$ -algèbre, on note $X_{A}$ la $A$ -variété obtenue par changement de base. Lorsque $A=\bar{K}$ , on utilise plutôt $\bar{X}$ au lieu de $X_{\bar{K}}$ et on garde plus généralement cette notation pour toute variété définie sur $\bar{K}$ , même si elle n’admet pas forcément de $K$ -forme. Il en va de même pour les $K$ -groupes algébriques, les $K$ -liens et les $K$ -gerbes, notés respectivement $G$ , $L$ et ${\mathcal{M}}$ dans la suite.

Si $G$ est un $K$ -groupe algébrique linéaire, on note :

• ∙ $G^{\circ }$ la composante neutre de $G$  ;

• ∙ $G^{\text{f}}=G/G^{\circ }$ le groupe (fini) des composantes connexes de $G$  ;

• ∙ $G^{\text{u}}$ le radical unipotent de $G^{\circ }$  ;

• ∙ $G^{\text{red}}=G^{\circ }/G^{\text{u}}$ , qui est un groupe réductif ;

• ∙ $G^{\text{ss}}=D(G^{\text{red}})=[G^{\text{red}},G^{\text{red}}]$ , qui est un groupe semi-simple ;

• ∙ $G^{\text{tor}}=G^{\text{red}}/G^{\text{ss}}$ , qui est un tore ;

• ∙ $G^{\text{ssu}}=\ker [G^{\circ }{\twoheadrightarrow}G^{\text{tor}}]$ , qui est une extension de $G^{\text{ss}}$ par $G^{\text{u}}$  ;

• ∙ $G^{\text{torf}}=G/G^{\text{ssu}}$ , qui est une extension de $G^{\text{f}}$ par $G^{\text{tor}}$  ;

qui sont tous définis sur $K$ .

2.1 L’obstruction de Brauer–Manin

Pour des détails sur l’obstruction de Brauer–Manin, on renvoie le lecteur vers [Sko01, § 5.1]. Pour une variété $X$ sur un corps de nombres $k$ , on considère le groupe de Brauer non ramifié $\text{Br}_{\text{nr}}X$ . Ce dernier correspond au groupe de Brauer d’une compactification lisse de $X$ (laquelle existe toujours sur un corps de caractéristique nulle d’après les théorèmes de Nagata et Hironaka). Pour $v\in \unicode[STIX]{x1D6FA}_{k}$ , on désigne par $\text{inv}_{v}:\text{Br}\,k_{v}\rightarrow \mathbb{Q}/\mathbb{Z}$ l’invariant de Hasse tel qu’il est défini par la théorie du corps de classes locale. On considère le plongement diagonal de $X(k)$ dans le produit $\prod _{v\in \unicode[STIX]{x1D6FA}_{k}}X(k_{v})$ . Alors on peut définir le sous-ensemble $[\prod _{v\in \unicode[STIX]{x1D6FA}_{k}}X(k_{v})]^{\text{Br}_{\text{nr}}}$ des familles de points locaux telles que

$$\begin{eqnarray}\mathop{\sum }_{v\in \unicode[STIX]{x1D6FA}_{k}}\text{inv}_{v}(\unicode[STIX]{x1D6FC}(P_{v}))=0,\quad \forall \,\unicode[STIX]{x1D6FC}\in \text{Br}_{\text{nr}}X,\end{eqnarray}$$

où $\unicode[STIX]{x1D6FC}(P_{v})\in \text{Br}\,k_{v}$ désigne l’application d’évaluation de $\unicode[STIX]{x1D6FC}$ au point $P_{v}$ . Remarquons que la somme précédente est finie pour les éléments $\unicode[STIX]{x1D6FC}\in \text{Br}_{\text{nr}}X$ . L’ensemble $[\prod _{v\in \unicode[STIX]{x1D6FA}_{k}}X(k_{v})]^{\text{Br}_{\text{nr}}}$ est dit ensemble de Brauer–Manin. La théorie du corps de classes globale nous fournit alors les inclusions suivantes :

$$\begin{eqnarray}\overline{X(k)}\subseteq \bigg[\mathop{\prod }_{v\in \unicode[STIX]{x1D6FA}_{k}}X(k_{v})\bigg]^{\text{Br}_{\text{nr}}}\subseteq \mathop{\prod }_{v\in \unicode[STIX]{x1D6FA}_{k}}X(k_{v}),\end{eqnarray}$$

où $\overline{X(k)}$ désigne l’adhérence de $X(k)$ dans le produit. Puisque l’approximation faible établit l’égalité entre les ensembles de droite et de gauche, l’ensemble de Brauer–Manin fournit une obstruction à l’approximation faible dès que l’inclusion de droite est stricte. De même, si l’ensemble de Brauer–Manin est vide alors que le produit tout entier ne l’est pas, on trouve une obstruction au principe de Hasse.

Une conjecture de Colliot-Thélène implique l’égalité $\overline{X(k)}=[\prod _{v\in \unicode[STIX]{x1D6FA}_{k}}X(k_{v})]^{\text{Br}_{\text{nr}}}$ pour tout espace homogène $X$ d’un groupe linéaire connexe $G$ (cf. [CT03, Intro]). On dit alors que l’obstruction de Brauer–Manin est la seule obstruction au principe de Hasse et à l’approximation faible.

2.2 2-cohomologie non abélienne

Soit $K$ un corps parfait. On fixe une clôture algébrique $\bar{K}$ de $K$ et on note $\unicode[STIX]{x1D6E4}_{K}:=\text{Gal}(\bar{K}/K)$ . Dans toute la suite, on munit $\text{Spec}\,(K)$ du petit site étale.

Les notions de $K$ -lien et de $K$ -gerbe sont importantes pour définir et étudier la cohomologie galoisienne en degré $2$ des groupes algébriques non commutatifs. On présente ici plusieurs points de vue différents, et néanmoins équivalents, sur ces notions, que l’on utilisera dans la suite du texte.

On rappelle que tous les groupes algébriques sont supposés lisses.

2.2.1 Liens

On dispose de deux notions de $K$ -lien : la notion abstraite de Giraud (cf. [Gir71, IV.1]) et la version concrète de Borovoi (cf. [Bor93, § 1]), dont une première version avait été présentée par Springer dans [Spr66] et dont la généralisation aux corps de caractéristique positive se trouve dans [FSS98].

Liens au sens de Giraud

On considère la catégorie fibrée (et même scindée) sur le petit site étale de $\text{Spec}\,K$ , notée $\text{}\underline{\text{LI}}(K)$ , définie de la façon suivante : la catégorie fibre en $\text{Spec}\,A$ pour une $K$ -algèbre étale $A$ a pour objets les faisceaux en groupes sur $\text{Spec}\,A$ , et si $H$ et $G$ sont des $A$ -faisceaux en groupes, un morphisme de $H$ vers $G$ dans $\text{}\underline{\text{LI}}(K)(A)$ est une section sur $\text{Spec}\,A$ du faisceau quotient $\text{}\underline{\text{Int}}(G)\backslash \text{}\underline{\text{Hom}}_{A\text{-gr}}(H,G)$ . On définit alors le champ (scindé) des $K$ -liens, noté $\text{}\underline{\text{LIENS}}(K)$ , comme le champ associé au préchamp $\text{}\underline{\text{LI}}(K)$ . Un lien sur $\text{Spec}\,K$ est alors un objet de la catégorie fibre $\text{}\underline{\text{Liens}}(K)$ de $\text{}\underline{\text{LIENS}}(K)$ en $\text{Spec}\,K$ . On dispose en particulier d’un morphisme de $K$ -champs (scindés)

$$\begin{eqnarray}\text{}\underline{\text{lien}}:\text{}\underline{\text{FAISCGR}}(K)\rightarrow \text{}\underline{\text{LIENS}}(K),\end{eqnarray}$$

qui à un faisceau en groupes $G$ associe le lien, noté $\text{}\underline{\text{lien}}(G)$ , défini par ce faisceau.

Pour la suite, on note $\text{}\underline{\text{Gralg}}(\bar{K})$ la catégorie dont les objets sont les $\bar{K}$ -groupes algébriques linéaires lisses, et les morphismes d’un $\bar{K}$ -groupe $\bar{H}$ vers un $\bar{K}$ -groupe $\bar{G}$ sont les morphismes de $\bar{K}$ -groupes algébriques $\bar{H}\rightarrow \bar{G}$ modulo $\text{Int}(\bar{G})$ . On dispose alors d’un foncteur naturel $\text{}\underline{\text{lien}}:\text{}\underline{\text{Gralg}}(\bar{K})\rightarrow \text{}\underline{\text{Liens}}(\bar{K})$ réalisant la première catégorie comme une sous-catégorie de la seconde.

On peut alors définir la catégorie $\text{}\underline{\text{Lialg}}(K)$ comme le produit 2-fibré suivant (voir par exemple [Sta18, 02X9]) :

$$\begin{eqnarray}\text{}\underline{\text{Lialg}}(K):=\text{}\underline{\text{Liens}}(K)\times _{\text{}\underline{\text{Liens}}(\bar{K})}\text{}\underline{\text{Gralg}}(\bar{K}).\end{eqnarray}$$

Plus concrètement, un objet de $\text{}\underline{\text{Lialg}}(K)$ est un triplet $(L,\bar{G},\unicode[STIX]{x1D711})$ , où $L$ est un lien sur $\text{Spec}\,(K)$ , $\bar{G}$ un $\bar{K}$ -groupe linéaire lisse et $f$ un isomorphisme $\unicode[STIX]{x1D711}:L_{\bar{K}}\xrightarrow[{}]{{\sim}}\text{}\underline{\text{lien}}(\bar{G})$ de liens sur $\text{Spec}\,(\bar{K})$ ; un morphisme $(M,\bar{H},\unicode[STIX]{x1D713})\rightarrow (L,\bar{G},\unicode[STIX]{x1D711})$ est un couple $(f,g)$ , où $f:M\rightarrow L$ est un morphisme de liens sur $\text{Spec}\,(K)$ et $g:\bar{H}\rightarrow \bar{G}$ un morphisme de $\bar{K}$ -groupes algébriques modulo $\text{Int}(\bar{H})$ , tel que $\unicode[STIX]{x1D711}\circ f_{\bar{K}}=\text{}\underline{\text{lien}}(g)\circ \unicode[STIX]{x1D713}$ . Les objets $(L,\bar{G},\unicode[STIX]{x1D711})$ de $\text{}\underline{\text{Lialg}}(K)$ sont appelés liens algébriques sur $\text{Spec}\,K$ , et ils seront parfois notés abusivement $L$ .

Remarquons enfin que, puisque toute $\bar{K}$ -algèbre étale est un produit direct de copies de $\bar{K}$ , le corollaire 9.29 de [Gir64] assure qu’une donnée de descente sur une $K$ -algèbre étale $A=\prod _{i\in I}K_{i}$ avec $K_{i}/K$ des extensions de corps correspond à des données de descente respectives sur chacun des $K_{i}$ . On en déduit que pour étudier les champs sur le petit site étale de $\text{Spec}\,K$ , il suffit de se restreindre aux extensions finies de $K$ (qui sont toutes séparables puisque $K$ est parfait).

Liens au sens de Springer–Borovoi

Présentons maintenant la seconde notion de $K$ -lien. Soit $\bar{G}$ un $\bar{K}$ -groupe algébrique linéaire lisse. Rappelons (cf. [Bor93, § 1] ou encore [FSS98, § 1]) que le groupe $\text{SAut}(\bar{G}/K)$ des automorphismes semi-algébriques de $\bar{G}$ sur $K$ (noté aussi $\text{SAut}(\bar{G})$ lorsque $K$ est sous-entendu) est formé des diagrammes commutatifs de la forme

pour un certain $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}_{K}$ et où $\text{Sp}\,\unicode[STIX]{x1D70E}$ désigne l’automorphisme de $\text{Spec}\,\bar{K}$ induit par $\unicode[STIX]{x1D70E}$ sur le corps $\bar{K}$ . On peut aussi voir ces objets comme des morphismes de $\bar{K}$ -groupes $\unicode[STIX]{x1D70E}_{\ast }\bar{G}\rightarrow \bar{G}$ , où $\unicode[STIX]{x1D70E}_{\ast }\bar{G}$ est le $\bar{K}$ -groupe algébrique $\bar{G}$ muni du morphisme structurel ‘tordu’

$$\begin{eqnarray}\bar{G}\rightarrow \text{Spec}\,\bar{K}\xrightarrow[{}]{\text{Sp}\,\unicode[STIX]{x1D70E}^{-1}}\text{Spec}\,\bar{K}.\end{eqnarray}$$

Ou encore, en considérant le $\bar{K}$ -groupe $(\text{Sp}\,\unicode[STIX]{x1D70E})^{\ast }\bar{G}$ , on peut vérifier aisément qu’il est canoniquement isomorphe à $\unicode[STIX]{x1D70E}_{\ast }\bar{G}$ en tant que $\bar{K}$ -groupe, ce qui fait que l’on peut remplacer $\unicode[STIX]{x1D70E}_{\ast }\bar{G}$ par $(\text{Sp}\,\unicode[STIX]{x1D70E})^{\ast }\bar{G}$ ci-dessus.

Enfin, on rappelle que l’on dispose d’une suite exacte

$$\begin{eqnarray}1\rightarrow \text{Aut}_{\bar{K}}(\bar{G})\rightarrow \text{SAut}(\bar{G})\rightarrow \unicode[STIX]{x1D6E4}_{K},\end{eqnarray}$$

ainsi que du groupe quotient $\text{SOut}(\bar{G}):=\text{SAut}(\bar{G})/\text{Int}\,(\bar{G})$ , où $\text{Int}\,(\bar{G})$ désigne l’image du morphisme $\bar{G}\rightarrow \text{Aut}(\bar{G})$ induit par la conjugaison.

Un $K$ -lien sur $\bar{G}$ est la donnée d’un morphisme de groupes continu $\unicode[STIX]{x1D705}:\unicode[STIX]{x1D6E4}_{K}\rightarrow \text{SOut}(\bar{G})$ qui scinde la suite exacte naturelle

$$\begin{eqnarray}1\rightarrow \text{Out}_{\bar{K}}(\bar{G})\rightarrow \text{SOut}(\bar{G})\rightarrow \unicode[STIX]{x1D6E4}_{K},\end{eqnarray}$$

et qui se relève en une section continue $f:\unicode[STIX]{x1D6E4}_{K}\rightarrow \text{SAut}(\bar{G})$ , On rappelle la définition de continuité dans ce contexte (cf. [FSS98, 1.10]). On sait que $\bar{G}$ admet une $K^{\prime }$ -forme pour une certaine extension finie $K^{\prime }/K$ . Cette $K^{\prime }$ -forme définit naturellement (cf. [FSS98, 1.4]) un scindage $s:\unicode[STIX]{x1D6E4}_{K^{\prime }}\rightarrow \text{SOut}(\bar{G}/K^{\prime })\subset \text{SOut}(\bar{G}/K)$ . L’application $f$ est dite continue si le morphisme

$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{K^{\prime }}\rightarrow \text{Aut}_{\bar{K}}(\bar{G}):s_{\unicode[STIX]{x1D70F}}^{-1}f_{\unicode[STIX]{x1D70E}}^{-1}f_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}},\end{eqnarray}$$

est localement constant pour tout $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}_{K}$ .

On dispose également dans ce contexte de la notion suivante de morphisme de $K$ -liens : si $(\bar{G},\unicode[STIX]{x1D705})$ et $(\bar{H},\unicode[STIX]{x1D706})$ sont deux $K$ -liens, considérons les morphismes de $\bar{K}$ -groupes $\unicode[STIX]{x1D711}:\bar{G}\rightarrow \bar{H}$ tels qu’il existe des relevés continus $g:\unicode[STIX]{x1D6E4}_{K}\rightarrow \text{SAut}(\bar{G})$ et $h:\unicode[STIX]{x1D6E4}_{K}\rightarrow \text{SAut}(\bar{H})$ de $\unicode[STIX]{x1D705}$ et $\unicode[STIX]{x1D706}$ respectivement, de sorte que pour tout $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}_{K}$ , le diagramme suivant de $\bar{K}$ -groupes

commute (et où la signification de $\unicode[STIX]{x1D70E}_{\ast }\unicode[STIX]{x1D711}$ est évidente). On a alors une action naturelle de $\text{Int}\,(\bar{H})$ sur ces morphismes, ce qui permet de définir un morphisme de liens $\unicode[STIX]{x1D711}:(\bar{G},\unicode[STIX]{x1D707})\rightarrow (\bar{H},\unicode[STIX]{x1D705})$ comme une classe de morphismes au sens précédent modulo $\text{Int}\,(\bar{H})$ . On a ainsi défini une catégorie, notée $\text{}\underline{K\text{-Liens}}$ .

Comparaison I

On dispose d’une équivalence de catégories naturelle $\text{}\underline{\text{Lialg}}(K)\rightarrow \text{}\underline{K\text{-Liens}}$ . Elle est définie ainsi : soit $(L,\bar{G},\unicode[STIX]{x1D711})$ un objet de $\text{}\underline{\text{Lialg}}(K)$ . Puisque $L$ est un lien sur $\text{Spec}\,(K)$ et $\unicode[STIX]{x1D711}:L_{\bar{K}}\rightarrow \text{}\underline{\text{lien}}(\bar{G})$ un isomorphisme de liens sur $\bar{K}$ , on dispose d’une donnée de descente naturelle sur $\text{}\underline{\text{lien}}(\bar{G})$ pour l’extension $\bar{K}/K$ , c’est-à dire que pour tout $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}_{K}$ , on a un isomorphisme canonique dans $\text{}\underline{\text{Liens}}(\bar{K})$ de la forme

$$\begin{eqnarray}f_{\unicode[STIX]{x1D70E}}:\text{}\underline{\text{lien}}(\unicode[STIX]{x1D70E}_{\ast }\bar{G})\xrightarrow[{}]{(\text{Sp}\,\unicode[STIX]{x1D70E})^{\ast }\unicode[STIX]{x1D711}^{-1}}(\text{Sp}\,\unicode[STIX]{x1D70E})^{\ast }L_{\bar{K}}\rightarrow L_{\bar{K}}\xrightarrow[{}]{\unicode[STIX]{x1D711}}\text{}\underline{\text{lien}}(\bar{G}),\end{eqnarray}$$

vérifiant $f_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}=f_{\unicode[STIX]{x1D70E}}\circ (\text{Sp}\,\unicode[STIX]{x1D70E})^{\ast }f_{\unicode[STIX]{x1D70F}}$ , où la première flèche se déduit de [Gir71, V.1.2.2.2] et de l’isomorphisme $(\text{Sp}\,\unicode[STIX]{x1D70E})^{\ast }\bar{G}\cong \unicode[STIX]{x1D70E}_{\ast }\bar{G}$ . Or, puisque

$$\begin{eqnarray}\text{Isom}_{\text{}\underline{\text{Liens}}(\bar{K})}(\text{}\underline{\text{lien}}(\unicode[STIX]{x1D70E}_{\ast }\bar{G}),\text{}\underline{\text{lien}}(\bar{G}))=\text{Int}\,(\bar{G})\backslash \text{Isom}_{\bar{K}\text{-gr}}(\unicode[STIX]{x1D70E}_{\ast }\bar{G},\bar{G}),\end{eqnarray}$$

et que $\text{Isom}_{\bar{K}\text{-gr}}(\unicode[STIX]{x1D70E}_{\ast }\bar{G},\bar{G})$ correspond à la préimage de $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}_{K}$ par rapport au morphisme naturel $\text{SAut}(\bar{G})\rightarrow \unicode[STIX]{x1D6E4}_{K}$ , on en déduit que la donnée de descente $(f_{\unicode[STIX]{x1D70E}})$ définit un morphisme de groupes $\unicode[STIX]{x1D705}_{L}:\unicode[STIX]{x1D6E4}_{K}\rightarrow \text{SOut}(\bar{G})$ scindant le morphisme $\text{SOut}(\bar{G})\rightarrow \unicode[STIX]{x1D6E4}_{K}$ , dont on vérifie qu’il est continu et qu’il se relève en une application continue $\unicode[STIX]{x1D6E4}_{K}\rightarrow \text{SAut}(\bar{G})$ (on utilise que l’isomorphisme entre $L_{\bar{K}}$ et $\text{}\underline{\text{lien}}(\bar{G})$ est défini localement pour la topologie étale, donc sur une extension finie de $K$ ). Donc $(\bar{G},\unicode[STIX]{x1D705}_{L})$ est un $K$ -lien.

Vérifions que l’on a bien défini un foncteur $\text{}\underline{\text{Lialg}}(K)\rightarrow \text{}\underline{K\text{-Liens}}$ . Soit un morphisme $\unicode[STIX]{x1D70F}:L=(L,\bar{G},\unicode[STIX]{x1D711})\rightarrow M=(M,\bar{H},\unicode[STIX]{x1D713})$ dans $\text{}\underline{\text{Lialg}}(K)$ . On a construit les $K$ -liens $(\bar{G},\unicode[STIX]{x1D705}_{L})$ et $(\bar{H},\unicode[STIX]{x1D705}_{M})$ associés respectivement à $L$ et $M$ . La construction assure que $\unicode[STIX]{x1D70F}$ induit un morphisme de $\bar{K}$ -groupes algébriques $\bar{\unicode[STIX]{x1D70F}}:\bar{G}\rightarrow \bar{H}$ défini modulo $\text{Int}\,(\bar{H})$ . On a le diagramme commutatif suivant dans $\text{}\underline{\text{Liens}}(\bar{K})$ .

Or $\unicode[STIX]{x1D70F}:L\rightarrow M$ est un morphisme dans $\text{}\underline{\text{Liens}}(K)$ , donc $\bar{\unicode[STIX]{x1D70F}}$ est muni d’une donnée de descente naturelle pour l’extension $\bar{K}/K$ , c’est-à dire que pour tout $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}_{K}$ , on a un diagramme commutatif dans $\text{}\underline{\text{Liens}}(\bar{K})$ de la forme

où $g_{\unicode[STIX]{x1D70E}}$ et $h_{\unicode[STIX]{x1D70E}}$ proviennent (via $\unicode[STIX]{x1D711}$ et $\unicode[STIX]{x1D713}$ ) des données de descente respectives pour $L_{\bar{K}}$ et $M_{\bar{K}}$ . On vérifie alors que ces données de descente définissent un morphisme $(\bar{G}_{L},\unicode[STIX]{x1D705}_{L})\rightarrow (\bar{G}_{M},\unicode[STIX]{x1D705}_{M})$ dans la catégorie $\text{}\underline{K\text{-Liens}}$ . D’où un foncteur $\text{}\underline{\text{Lialg}}(K)\rightarrow \text{}\underline{K\text{-Liens}}$ .

Montrons que le foncteur ainsi défini est une équivalence de catégories. Un quasi-inverse est donné par le foncteur suivant : si $(\bar{G},\unicode[STIX]{x1D705})$ est un $K$ -lien, alors il existe une extension finie galoisienne $K^{\prime }/K$ et une $K^{\prime }$ -forme $G^{\prime }$ de $\bar{G}$ correspondant à un scindage continu

$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{K^{\prime }}\rightarrow \text{SAut}(\bar{G}/K^{\prime })\subset \text{SAut}(\bar{G}/K)\end{eqnarray}$$

du morphisme $\text{SAut}(\bar{G}/K^{\prime })\rightarrow \unicode[STIX]{x1D6E4}_{K^{\prime }}$ ; cf. [FSS98, 1.4]. Par continuité (cf. [FSS98, 1.10]) on sait que, quitte à agrandir $K^{\prime }$ , on peut supposer que ce scindage relève $\unicode[STIX]{x1D705}$ . On dispose alors de l’objet $\text{}\underline{\text{lien}}(G^{\prime })$ dans la catégorie $\text{}\underline{\text{Liens}}(K^{\prime })$ qui est bien défini à isomorphisme unique près. En effet, par continuité, deux scindages différents induisant des $K^{\prime }$ -formes $G_{1}^{\prime }$ et $G_{2}^{\prime }$ sont conjugués sur une extension galoisienne finie $K^{\prime \prime }/K^{\prime }$ . Cette donnée, jointe aux isomorphismes $\text{}\underline{\text{lien}}(\bar{G}_{i}^{\prime })\rightarrow \text{}\underline{\text{lien}}(\bar{G})$ sur $\bar{K}$ fixent un unique isomorphisme de liens sur $K^{\prime \prime }$ . Le fait que les deux scindages relèvent $\unicode[STIX]{x1D705}$ induit une donnée de descente sur ce $K^{\prime \prime }$ -morphisme, induisant un unique $K^{\prime }$ -isomorphisme $\text{}\underline{\text{lien}}(G_{1}^{\prime })\rightarrow \text{}\underline{\text{lien}}(G_{2}^{\prime })$ . Ensuite, on peut définir un relèvement continu de l’application $\unicode[STIX]{x1D705}:\unicode[STIX]{x1D6E4}_{K}\rightarrow \text{SOut}(\bar{G})$ en prenant le scindage sur $\unicode[STIX]{x1D6E4}_{K^{\prime }}$ et des translatés de ce scindage pour les classes latérales de $\unicode[STIX]{x1D6E4}_{K^{\prime }}{\vartriangleleft}\unicode[STIX]{x1D6E4}_{K}$ . On en déduit ainsi pour chaque $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}_{K^{\prime }/K}$ un morphisme

$$\begin{eqnarray}f_{\unicode[STIX]{x1D70E}}:(\text{Sp}\,\unicode[STIX]{x1D70E})^{\ast }\text{}\underline{\text{lien}}(G^{\prime })=\text{}\underline{\text{lien}}(\unicode[STIX]{x1D70E}_{\ast }\bar{G}^{\prime })\rightarrow \text{}\underline{\text{lien}}(G^{\prime })\end{eqnarray}$$

dans la catégorie $\text{Liens}(K^{\prime })$ . Puisque $\unicode[STIX]{x1D705}$ est un morphisme de groupes, ces morphismes vérifient $f_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}=f_{\unicode[STIX]{x1D70E}}\circ ((\text{Sp}\,\unicode[STIX]{x1D70E})^{\ast }f_{\unicode[STIX]{x1D70F}})$ . Par conséquent, les morphismes $(f_{\unicode[STIX]{x1D70E}})$ définissent une donnée de descente sur $\text{}\underline{\text{lien}}(G^{\prime })$ . Comme la catégorie fibrée $\text{}\underline{\text{LIENS}}(K)$ des liens est un $K$ -champ, cette donnée de descente définit un objet $L_{\unicode[STIX]{x1D705}}$ de $\text{}\underline{\text{Liens}}(K)$ et un isomorphisme $\unicode[STIX]{x1D711}:L_{\unicode[STIX]{x1D705},K^{\prime }}\rightarrow \text{}\underline{\text{lien}}(G^{\prime })$ , lequel induit un isomorphisme $\unicode[STIX]{x1D711}:L_{\unicode[STIX]{x1D705},\bar{K}}\rightarrow \text{}\underline{\text{lien}}(\bar{G})$ et donc $(L_{\unicode[STIX]{x1D705}},\bar{G},\unicode[STIX]{x1D711})$ est dans $\text{}\underline{\text{Lialg}}(K)$ . De même, si $\unicode[STIX]{x1D70F}:(\bar{G},\unicode[STIX]{x1D705})\rightarrow (\bar{H},\unicode[STIX]{x1D706})$ est un morphisme dans $\text{}\underline{K\text{-Liens}}$ , on vérifie que celui-ci définit un unique morphisme $\unicode[STIX]{x1D70F}^{\prime }:\text{}\underline{\text{lien}}(G^{\prime })\rightarrow \text{}\underline{\text{lien}}(H^{\prime })$ pour des $K^{\prime }$ -formes $G^{\prime }$ et $H^{\prime }$ de $\bar{G}$ et $\bar{H}$ respectivement. On vérifie ensuite que ce morphisme dans $\text{}\underline{\text{Lialg}}(K^{\prime })$ est muni d’une donnée de descente, ce qui permet d’en déduire un morphisme $\widetilde{\unicode[STIX]{x1D70F}}:L_{\unicode[STIX]{x1D705}}\rightarrow L_{\unicode[STIX]{x1D706}}$ puisque $\text{}\underline{\text{LIENS}}(K)$ est un $K$ -champ. Cela définit bien le foncteur souhaité $\text{}\underline{K\text{-Liens}}\rightarrow \text{}\underline{\text{Lialg}}(K)$ . On peut alors vérifier que celui-ci est bien un quasi-inverse du premier.

2.2.2 2-cohomologie non abélienne

On dispose de trois façons équivalentes de voir la 2-cohomologie galoisienne non abélienne. Les deux premières, correspondant aux points de vue des cocycles et des extensions, sont bien connues dans le cadre de la cohomologie des groupes non abélienne classique et s’adaptent donc au cadre de la cohomologie galoisienne via la notion de $K$ -lien à la Springer–Borovoi. Le troisième point de vue, celui des gerbes, est issu du point de vue plus abstrait des liens à la Giraud.

Cocycles

Soit $L=(\bar{G},\unicode[STIX]{x1D705})$ un $K$ -lien. On munit $\bar{G}(\bar{K})$ de la topologie discrète. Un $2$ -cocycle à valeurs dans $L$ est un couple $(f,u)$ , où $f:\unicode[STIX]{x1D6E4}_{K}\rightarrow \text{SAut}(\bar{G})$ est une application continue qui relève $\unicode[STIX]{x1D705}$ et $u:\unicode[STIX]{x1D6E4}_{K}\times \unicode[STIX]{x1D6E4}_{K}\rightarrow \bar{G}(\bar{K})$ est une application continue vérifiant, pour tout $\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F},\unicode[STIX]{x1D710}\in \unicode[STIX]{x1D6E4}_{K}$ ,

$$\begin{eqnarray}\displaystyle & \displaystyle f_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}}=\text{Int}\,(u_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}})\circ f_{\unicode[STIX]{x1D70E}}\circ f_{\unicode[STIX]{x1D70F}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle u_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\unicode[STIX]{x1D710}}\cdot f_{\unicode[STIX]{x1D70E}}(u_{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D710}})=u_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},\unicode[STIX]{x1D710}}\cdot u_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}}, & \displaystyle \nonumber\end{eqnarray}$$

où $\text{Int}\,(u_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}})$ désigne le morphisme de conjugaison par l’élément $u_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}}$ .

Deux $2$ -cocycles $(f,u)$ et $(f^{\prime },u^{\prime })$ sont dits équivalents s’il existe une application continue $c:\unicode[STIX]{x1D6E4}_{K}\rightarrow \bar{G}(\bar{K})$ telle que pour tout $\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6E4}_{K}$ , on a

$$\begin{eqnarray}\displaystyle & \displaystyle f_{\unicode[STIX]{x1D70E}}^{\prime }=\text{Int}\,(c_{\unicode[STIX]{x1D70E}})\circ f_{\unicode[STIX]{x1D70E}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle u_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}}^{\prime }=c_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\cdot u_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}}\cdot f_{\unicode[STIX]{x1D70E}}(c_{\unicode[STIX]{x1D70F}})^{-1}\cdot c_{\unicode[STIX]{x1D70E}}^{-1}. & \displaystyle \nonumber\end{eqnarray}$$

L’ensemble des $2$ -cocycles modulo cette relation d’équivalence est noté $H^{2}(K,L)$ , ou $H^{2}(K,G)$ si $L=\text{}\underline{\text{lien}}(G)$ . Une classe dans $H^{2}(K,L)$ est dite neutre si elle est représentable par un $2$ -cocycle de la forme $(f,1)$ . Elle correspond alors à une $k$ -forme $G$ de $\bar{G}$ (cf. [Bor93, 1.4]) et on la note alors $n(G)$ .

Extensions

Soit $L=(\bar{G},\unicode[STIX]{x1D705})$ un $K$ -lien. On munit toujours $\bar{G}(\bar{K})$ de la topologie discrète. On définit une extension liée par $L$ comme une suite exacte de groupes topologiques

$$\begin{eqnarray}1\rightarrow \bar{G}(\bar{K})\rightarrow E\rightarrow \unicode[STIX]{x1D6E4}_{K}\rightarrow 1,\end{eqnarray}$$

telle que le morphisme naturel $\unicode[STIX]{x1D6E4}_{K}\rightarrow \text{Out}(G(\bar{K}))$ induit par cette suite exacte soit égal à la composée de $\unicode[STIX]{x1D705}$ avec le morphisme naturel $\text{SOut}(\bar{G})\rightarrow \text{Out}(G(\bar{K}))$ . On rappelle que par suite exacte de groupes topologiques on entend que la flèche de gauche induit un homéomorphisme avec son image, qui est un fermé de $E$ , alors que la flèche de droite est un morphisme ouvert.

On note $\text{Ext}(\unicode[STIX]{x1D6E4}_{K},L)$ l’ensemble des classes d’équivalence de telles extensions. Une extension est dite neutre si elle admet une section qui est un morphisme continu.

Gerbes

Une $K$ -gerbe est un champ en groupoïdes ${\mathcal{M}}$ sur le petit site étale de $\text{Spec}\,(K)$ tel que :

• ∙ il existe une $K$ -algèbre étale $A/K$ telle que ${\mathcal{M}}(A)\neq \emptyset$ ;

• ∙ pour toute $K$ -algèbre étale $A$ , pour tout $m,m^{\prime }\in {\mathcal{M}}(A)$ , il existe une $A$ -algèbre étale $A^{\prime }$ et un isomorphisme $m\xrightarrow[{}]{{\sim}}m^{\prime }$ dans ${\mathcal{M}}(A^{\prime })$ .

Comme on l’a mentionné dans la section précédente, on peut déduire de [Gir64, Corollaire 9.29] que l’on peut remplacer ‘algèbre étale’ par ‘extension finie’ dans les deux points ci-dessus.

Par exemple, pour tout $K$ -groupe algébrique $G$ (ou plus généralement un faisceau étale en groupes), le champ des $G$ -torseurs, noté $\text{}\underline{\text{TORS}}(G)$ , est une $K$ -gerbe.

À une $K$ -gerbe ${\mathcal{M}}$ on associe son lien $L_{{\mathcal{M}}}$ défini de la façon suivante : on choisit $m\in {\mathcal{M}}(K^{\prime })$ pour une extension finie galoisienne $K^{\prime }$ de $K$ . Pour tout $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}_{K}$ , on dispose du foncteur naturel ${\mathcal{M}}(K^{\prime })\rightarrow {\mathcal{M}}(K^{\prime })$ induit par $\text{Sp}\,\unicode[STIX]{x1D70E}$ . On note $\text{}^{\unicode[STIX]{x1D70E}}m$ l’image de $m$ par ce foncteur. Par définition, il existe une extension finie $K^{\prime \prime }/K^{\prime }$ telle que pour tout $\unicode[STIX]{x1D70E}\in \text{Gal}(K^{\prime }/K)$ , il existe un (iso)morphisme $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}:\text{}^{\unicode[STIX]{x1D70E}}m\rightarrow m$ dans la catégorie ${\mathcal{M}}(K^{\prime \prime })$ . On note alors $f_{\unicode[STIX]{x1D70E}}:\text{}\underline{\text{Aut}}(\text{}^{\unicode[STIX]{x1D70E}}m)\rightarrow \text{}\underline{\text{Aut}}(m)$ le morphisme de $K^{\prime \prime }$ -faisceaux en groupes défini par $f_{\unicode[STIX]{x1D70E}}(\unicode[STIX]{x1D6FC}):=\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}\circ \unicode[STIX]{x1D6FC}\circ {\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}}^{-1}$ . Or, d’après [Gir71, V.1.3.3.3], on a un isomorphisme naturel $\text{}\underline{\text{Aut}}(\text{}^{\unicode[STIX]{x1D70E}}m)\cong (\text{Sp}\,\unicode[STIX]{x1D70E})^{\ast }\text{}\underline{\text{Aut}}(m)$ . Donc on a défini un morphisme $f_{\unicode[STIX]{x1D70E}}:(\text{Sp}\,\unicode[STIX]{x1D70E})^{\ast }\text{}\underline{\text{Aut}}(m)\rightarrow \text{}\underline{\text{Aut}}(m)$ de $K^{\prime \prime }$ -faisceau en groupes, donc un morphisme de $K^{\prime \prime }$ -liens $f_{\unicode[STIX]{x1D70E}}:(\text{Sp}\,\unicode[STIX]{x1D70E})^{\ast }\text{}\underline{\text{lien}}(\text{}\underline{\text{Aut}}(m))\rightarrow \text{}\underline{\text{lien}}(\text{}\underline{\text{Aut}}(m))$ . On vérifie que cela munit $\text{}\underline{\text{lien}}(\text{}\underline{\text{Aut}}(m))$ d’une donnée de descente relativement à l’extension $K^{\prime \prime }/K$ , donc cela définit un lien sur $\text{Spec}\,K$ que l’on note $L_{{\mathcal{M}}}$ et, à isomorphisme unique près, ce lien ne dépend pas des choix de $K^{\prime }$ , $m$ , $K^{\prime \prime }$ , ni du choix des isomorphismes $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}$ . Si $\text{}\underline{\text{Aut}}(m)$ est représentable par un $\bar{K}$ -groupe linéaire lisse, alors on dispose d’un lien algébrique $L({\mathcal{M}})=(L_{{\mathcal{M}}},\text{}\underline{\text{Aut}}(m),\text{id}_{\text{}\underline{\text{lien}}(\text{}\underline{\text{Aut}}(m))})$ , bien défini à isomorphisme unique près dans $\text{}\underline{\text{Lialg}}(K)$ . Dans ce cas, on dit que ${\mathcal{M}}$ est une gerbe algébrique.

Un morphisme de $K$ -gerbes est un morphisme de $K$ -champs dont la source et le but sont des gerbes. Tout morphisme $\unicode[STIX]{x1D711}:{\mathcal{M}}\rightarrow {\mathcal{N}}$ de $K$ -gerbes (respectivement de $K$ -gerbes algébriques) induit un morphisme de $K$ -liens (respectivement de $K$ -liens algébriques) $\text{}\underline{\text{lien}}(\unicode[STIX]{x1D711})\,:\,L_{{\mathcal{M}}}\rightarrow L_{{\mathcal{N}}}$ (respectivement $\text{}\underline{\text{lien}}(\unicode[STIX]{x1D711})\,:\,L({\mathcal{M}})\rightarrow L({\mathcal{N}})$ ) ; cf. [Gir71, IV.2.2.3]. Le morphisme $\unicode[STIX]{x1D711}$ est dit lié par $\text{}\underline{\text{lien}}(\unicode[STIX]{x1D711})$ . Une équivalence (respectivement un morphisme injectif, respectivement surjectif) de $K$ -gerbes est un morphisme de gerbes lié par un isomorphisme (respectivement par un morphisme injectif, respectivement surjectif) de liens. Bien entendu, un morphisme de liens est dit injectif (respectivement surjectif) si le morphisme de $\bar{K}$ -groupes algébriques sous-jacent l’est.

Soit $L=(L,\bar{G},\unicode[STIX]{x1D711})$ un lien algébrique sur $\text{Spec}\,K$ au sens de Giraud. Une $K$ -gerbe liée par $L$ est un couple $({\mathcal{M}},\unicode[STIX]{x1D70C})$ , où ${\mathcal{M}}$ est une $K$ -gerbe et $\unicode[STIX]{x1D70C}:L({\mathcal{M}})\rightarrow L$ un isomorphisme de liens algébriques. Deux telles $K$ -gerbes $({\mathcal{M}},\unicode[STIX]{x1D70C})$ et $({\mathcal{M}}^{\prime },\unicode[STIX]{x1D70C}^{\prime })$ sont dites équivalentes s’il existe un (iso)morphisme de $K$ -gerbes $\unicode[STIX]{x1D6FC}:{\mathcal{M}}\rightarrow {\mathcal{M}}^{\prime }$ tel que $\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}^{\prime }\circ \text{}\underline{\text{lien}}(\unicode[STIX]{x1D6FC})$ .

On note $\text{Ger}(K,L)$ l’ensemble des classes d’équivalence de $K$ -gerbes algébriques liées par $L$ . La classe d’une gerbe ${\mathcal{M}}$ est dite neutre si ${\mathcal{M}}(K)\neq \emptyset$ . Le faisceau $\text{}\underline{\text{Aut}}(m)$ pour $m\in {\mathcal{M}}(K)$ est dans ce cas représenté par un $K$ -groupe algébrique $G$ qui est une $K$ -forme du groupe $\bar{G}$ sous-jacent à $L$ . On note alors $n(G)$ la classe de ${\mathcal{M}}$ .

Comparaison II

L’énoncé suivant affirme que les trois définitions précédentes sont équivalentes.

Proposition 2.1. Soit $L$ un $K$ -lien. Alors on a des bijections canoniques et fonctorielles :

$$\begin{eqnarray}H^{2}(K,L)\xrightarrow[{}]{{\sim}}\text{Ext}(\unicode[STIX]{x1D6E4}_{K},L)\xrightarrow[{}]{{\sim}}\text{Ger}(K,L),\end{eqnarray}$$

qui font correspondre les sous-ensembles de classes neutres de chacun des trois ensembles.

Démonstration.

On rappelle seulement la construction des différentes bijections.

Cocycles vers extensions. Étant donné un $2$ -cocycle $(f,u)$ , on construit le groupe $E:=\bar{G}(\bar{K})\times \unicode[STIX]{x1D6E4}_{K}$ avec le produit tordu suivant :

$$\begin{eqnarray}(g,\unicode[STIX]{x1D70E})\cdot (h,\unicode[STIX]{x1D70F}):=(g\cdot f_{\unicode[STIX]{x1D70E}}(h)\cdot u_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}}^{-1},\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}),\end{eqnarray}$$

et on vérifie qu’il s’insère dans une suite exacte courte

$$\begin{eqnarray}1\rightarrow \bar{G}(\bar{K})\rightarrow E\rightarrow \unicode[STIX]{x1D6E4}_{K}\rightarrow 1,\end{eqnarray}$$

dont le lien associé est clairement $L$ , ce qui définit la flèche $H^{2}(K,L)\rightarrow \text{Ext}(\unicode[STIX]{x1D6E4}_{K},L)$ .

Extensions vers gerbes. Soit une extension de groupes topologiques

$$\begin{eqnarray}1\rightarrow \bar{G}(\bar{K})\rightarrow E\xrightarrow[{}]{\unicode[STIX]{x1D70B}}\unicode[STIX]{x1D6E4}_{K}\rightarrow 1.\end{eqnarray}$$

Soit $A$ une $K$ -algèbre étale, dont on note $X_{A}:=\text{Hom}_{K\text{-}\text{alg}}(A,\bar{K})$ le $\unicode[STIX]{x1D6E4}_{K}$ -ensemble fini associé. On définit la catégorie ${\mathcal{M}}_{E}(A)$ dont les objets sont les paires $(Y,p)$ formées d’un ensemble discret $Y$ muni d’une action continue de $E$ et d’un morphisme $p:Y\rightarrow X_{A}$ qui est $E$ -équivariant (via le morphisme $\unicode[STIX]{x1D70B}$ ) et tel que l’action de $E$ sur $Y$ induise sur $Y$ une structure de $X_{A}$ -torseur sous $\bar{G}(\bar{K})$ (i.e. $\bar{G}(\bar{K})$ agit simplement transitivement sur les fibres de $p$ ). Un morphisme $(Y,p)\rightarrow (Y^{\prime },p^{\prime })$ dans la catégorie ${\mathcal{M}}_{E}(A)$ est une application $E$ -équivariante $\unicode[STIX]{x1D711}:Y\rightarrow Y^{\prime }$ au-dessus de $X_{A}$ .

On a ainsi défini une catégorie fibrée en groupoïdes sur le petit site étale de $\text{Spec}\,(K)$ .

Les topologies des groupes concernés (discrète pour $\bar{G}(\bar{K})$ , profinie pour $\unicode[STIX]{x1D6E4}_{K}$ ) et les propriétés des morphismes (ouverts et continus) nous disent que l’extension $E$ est localement scindée : il existe une extension finie $K^{\prime }$ de $K$ (contenue dans $\bar{K}$ ) telle que l’extension $E^{\prime }$ , obtenue en tirant $E$ en arrière par le morphisme $\unicode[STIX]{x1D6E4}_{K^{\prime }}\rightarrow \unicode[STIX]{x1D6E4}_{K}$ , est scindée. Une section $s:\unicode[STIX]{x1D6E4}_{K^{\prime }}\rightarrow E^{\prime }$ permet de définir un $\bar{G}(\bar{K})$ -torseur $p_{s}:Y_{s}:=E/s(\unicode[STIX]{x1D6E4}_{K^{\prime }})\rightarrow \unicode[STIX]{x1D6E4}_{K}/\unicode[STIX]{x1D6E4}_{K^{\prime }}\xrightarrow[{}]{{\sim}}X_{K^{\prime }}$ , de sorte que $(Y_{s},p_{s})$ est un objet de ${\mathcal{M}}_{E}(K^{\prime })$ . En particulier, ${\mathcal{M}}_{E}(K^{\prime })\neq \emptyset$ . Par un argument de continuité, on montre également que deux objets de ${\mathcal{M}}_{E}(K^{\prime })$ sont localement isomorphes, pour toute extension finie $K^{\prime }$ de $K$ (cela résulte du fait que deux sections de $E$ sont localement conjuguées par un élément de $\bar{G}(\bar{K})$ ).

Vérifions que ${\mathcal{M}}_{E}$ est un champ. Soit $K^{\prime }/K$ une extension finie de corps et $K^{\prime \prime }/K^{\prime }$ une extension finie galoisienne. On fixe un plongement $K^{\prime \prime }\subset \bar{K}$ . Notons $\unicode[STIX]{x1D6E4}:=\text{Gal}(K^{\prime \prime }/K^{\prime })$ . Le groupe $\unicode[STIX]{x1D6E4}$ agit naturellement (à droite) sur $X_{K^{\prime \prime }}$ via la formule $\unicode[STIX]{x1D719}\cdot \unicode[STIX]{x1D70E}:=\unicode[STIX]{x1D719}\circ \unicode[STIX]{x1D70E}$ pour $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}$ et $\unicode[STIX]{x1D719}\in X_{K^{\prime \prime }}$ . Ainsi, pour tout $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}$ , on peut expliciter le foncteur image inverse ${\mathcal{M}}_{E}(K^{\prime \prime })\rightarrow {\mathcal{M}}_{E}(K^{\prime \prime })$ induit par $\unicode[STIX]{x1D70E}$ , de la façon suivante : l’image d’un objet $(Y,p)$ de ${\mathcal{M}}_{E}(K^{\prime \prime })$ est l’objet $(Y^{\unicode[STIX]{x1D70E}},p_{\unicode[STIX]{x1D70E}})\in {\mathcal{M}}_{E}(K^{\prime \prime })$ défini par le diagramme cartésien suivant :

et on dispose de la description analogue pour les morphismes. On en déduit qu’une donnée de descente sur $(Y,p)$ relativement à l’extension $K^{\prime \prime }/K^{\prime }$ équivaut à la donnée, pour tout $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}$ , d’un (iso)morphisme $f_{\unicode[STIX]{x1D70E}}:(Y^{\unicode[STIX]{x1D70E}},p_{\unicode[STIX]{x1D70E}})\rightarrow (Y,p)$ , tel que pour tous $\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6E4}$ , $f_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}=f_{\unicode[STIX]{x1D70F}}\circ \unicode[STIX]{x1D70F}^{\ast }(f_{\unicode[STIX]{x1D70E}})$ . Par conséquent, cela équivaut à la donnée, pour tout $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}$ , d’une application $E$ -équivariante $h_{\unicode[STIX]{x1D70E}}:Y\rightarrow Y$ s’insérant dans le diagramme commutatif suivant :

de sorte que $h_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}=h_{\unicode[STIX]{x1D70E}}\circ h_{\unicode[STIX]{x1D70F}}$ . Cela définit donc une action (à gauche) de $\unicode[STIX]{x1D6E4}$ sur $Y$ compatible avec l’action (à gauche) de $\unicode[STIX]{x1D6E4}$ sur $X_{K^{\prime \prime }}$ (via $\unicode[STIX]{x1D70E}\cdot \unicode[STIX]{x1D719}:=\unicode[STIX]{x1D719}\circ \unicode[STIX]{x1D70E}^{-1}$ ). En outre, on voit que ces actions de $\unicode[STIX]{x1D6E4}$ commutent aux actions de $E$ sur $Y$ et $X_{K^{\prime \prime }}$ . Par conséquent, une telle donnée de descente permet de définir une application $p_{0}:Y_{0}:=Y/\unicode[STIX]{x1D6E4}\rightarrow X_{K^{\prime \prime }}/\unicode[STIX]{x1D6E4}=X_{K^{\prime }}$ $E$ -équivariante, et un élément $(Y_{0},p_{0})\in {\mathcal{M}}_{E}(K^{\prime })$ muni d’un isomorphisme entre son image dans ${\mathcal{M}}_{E}(K^{\prime \prime })$ et $(Y,p)$ , compatible à la donnée de descente. Par conséquent, les données de descente dans ${\mathcal{M}}_{E}$ sont effectives. Un raisonnement analogue assure que les données de descente pour les morphismes sont également effectives. Donc ${\mathcal{M}}_{E}$ est un $K$ -champ, localement non vide et localement connexe, donc c’est une $K$ -gerbe.

Enfin, si $K^{\prime }\subset \bar{K}$ , étant donné un objet $(Y,p)\in {\mathcal{M}}_{E}(K^{\prime })$ , on observe que le choix d’un point $y\in Y$ au-dessus du point naturel de $X_{K^{\prime }}$ fixe un isomorphisme entre le $L$ -faisceau en groupes $\text{}\underline{\text{Aut}}_{L}(Y,p)$ et $\bar{G}(\bar{K})\,\cap \,N_{E}(\text{}\underline{\text{Stab}}_{E}(y_{L}))$ . On en déduit alors un isomorphisme canonique de $K$ -liens (indépendant de $(Y,p)$ et de $y$ ) entre $L_{E}$ et $L$ .

Gerbes vers cocycles. Soit ${\mathcal{M}}$ une $K$ -gerbe algébrique et $\unicode[STIX]{x1D70F}:L({\mathcal{M}})\rightarrow L$ un isomorphisme. Posons alors $L=(\bar{G},\unicode[STIX]{x1D705})$ . Choisissons une section $m\in {\mathcal{M}}(K^{\prime })$ pour une extension finie galoisienne $K^{\prime }/K$ . Le morphisme $\unicode[STIX]{x1D70F}$ induit un isomorphisme de $\bar{K}$ -groupes $\bar{\unicode[STIX]{x1D70F}}:\text{}\underline{\text{Aut}}(m)\xrightarrow[{}]{{\sim}}\bar{G}$ , bien défini modulo $\text{Int}(\bar{G})$ . Suivant la construction du lien $L({\mathcal{M}})$ , on obtient pour $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}_{K}$ un isomorphisme $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}:\text{}^{\unicode[STIX]{x1D70E}}m\rightarrow m$ dans la catégorie ${\mathcal{M}}(K^{\prime \prime })$ , où $K^{\prime \prime }$ est une extension finie de $K^{\prime }$ , et l’isomorphisme naturel  nous permet par ailleurs de définir un morphisme de $\bar{K}$ -groupes $f_{\unicode[STIX]{x1D70E}}:\unicode[STIX]{x1D70E}_{\ast }\bar{G}\rightarrow \bar{G}$ par $f_{\unicode[STIX]{x1D70E}}(\unicode[STIX]{x1D6FC}):=\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}\circ \unicode[STIX]{x1D6FC}\circ {\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}}^{-1}$ . Le morphisme $f_{\unicode[STIX]{x1D70E}}$ est alors dans $\text{SAut}(\bar{G})$ et, puisque c’est avec ces morphismes que l’on construit le lien associé à ${\mathcal{M}}$ , son image dans $\text{SOut}(\bar{G})$ est exactement $\unicode[STIX]{x1D705}_{\unicode[STIX]{x1D70E}}$ . En outre, le fait que les morphismes $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}$ soient définis sur $K^{\prime \prime }$ assure que l’application $\unicode[STIX]{x1D70E}\mapsto f_{\unicode[STIX]{x1D70E}}$ est continue. Si l’on note alors  l’image du morphisme $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F}}$ par le foncteur induit par $\unicode[STIX]{x1D70E}$ et que l’on pose $u_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}}:=\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\circ {\text{}^{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70F}}}^{-1}\circ \unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}^{-1}\in \text{}\underline{\text{Aut}}(m)(\bar{K})=\bar{G}(\bar{K})$ (identification via  $\bar{\unicode[STIX]{x1D70F}}$ ), un calcul simple assure que l’on a les relations suivantes :

$$\begin{eqnarray}\displaystyle f_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}=\text{Int}\,(u_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}})\circ f_{\unicode[STIX]{x1D70E}}\circ f_{\unicode[STIX]{x1D70F}}\quad & & \displaystyle \text{dans }\text{SAut}(\bar{G}),\nonumber\\ \displaystyle u_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\unicode[STIX]{x1D710}}\cdot f_{\unicode[STIX]{x1D70E}}(u_{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D710}})=u_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},\unicode[STIX]{x1D710}}\cdot u_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}}\quad & & \displaystyle \text{dans }\bar{G}(\bar{K}).\nonumber\end{eqnarray}$$

Par conséquent $(f,u)\in Z^{2}(K,L)$ . En outre, on vérifie que des choix différents de $\bar{\unicode[STIX]{x1D70F}}$ et $m\in {\mathcal{M}}(\bar{K})$ définissent des cocycles équivalents à $(f,u)$ .◻

Remarque.

La correspondance entre gerbes et cocycles est détaillée dans [Bre94]. Pour le sens ‘gerbes vers cocycles’, cf. les sections 2.2 à 2.4 ; pour le sens ‘cocycles vers gerbes’, cf. les sections 2.6 à 2.8.

2.2.3 Fonctorialité

Soient $L=(\bar{G},\unicode[STIX]{x1D705})$ et $L^{\prime }=(\bar{G}^{\prime },\unicode[STIX]{x1D705}^{\prime })$ des $K$ -liens et soit $\unicode[STIX]{x1D711}:L\rightarrow L^{\prime }$ un morphisme de $K$ -liens. À la différence du cas classique, un tel morphisme n’induit pas forcément un morphisme entre les ensembles de 2-cohomologie non abélienne. Cependant, on a toujours une relation, notée

$$\begin{eqnarray}\unicode[STIX]{x1D711}^{(2)}:H^{2}(K,L)\multimap H^{2}(K,L^{\prime }),\end{eqnarray}$$

et qui est définie comme suit. On dit que deux classes $\unicode[STIX]{x1D702}\in H^{2}(K,L)$ et $\unicode[STIX]{x1D702}^{\prime }\in H^{2}(K,L^{\prime })$ sont reliées si :

Dans le langage des cocycles, s’il existe des cocycles $(f,u)$ et $(f^{\prime },u^{\prime })$ représentant respectivement $\unicode[STIX]{x1D702}$ et $\unicode[STIX]{x1D702}^{\prime }$ tels que, pour tout $g\in \bar{G}(\bar{K})$ et pour tout $\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6E4}_{K}$ ,

$$\begin{eqnarray}f_{\unicode[STIX]{x1D70E}}^{\prime }(\unicode[STIX]{x1D711}(g))=\unicode[STIX]{x1D711}(f_{\unicode[STIX]{x1D70E}}(g))\quad \text{et}\quad u_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}}^{\prime }=\unicode[STIX]{x1D711}(u_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}}).\end{eqnarray}$$

Dans le langage des extensions, s’il existe des extensions $E$ et $E^{\prime }$ représentant respectivement $\unicode[STIX]{x1D702}$ et $\unicode[STIX]{x1D702}^{\prime }$ et un morphisme d’extensions comme le suivant.

Dans le langage des gerbes, s’il existe des gerbes ${\mathcal{M}}$ et ${\mathcal{M}}^{\prime }$ représentant respectivement $\unicode[STIX]{x1D702}$ et $\unicode[STIX]{x1D702}^{\prime }$ et un morphisme de gerbes ${\mathcal{M}}\rightarrow {\mathcal{M}}^{\prime }$ lié par $\unicode[STIX]{x1D711}$ .

On rappelle qu’une telle relation peut être vide en général et que, dans le cas particulier où $\unicode[STIX]{x1D711}$ est surjective ou $\bar{G}^{\prime }$ est abélien, elle correspond à une application $H^{2}(K,L)\rightarrow H^{2}(K,L^{\prime })$ . Ceci est un exercice facile à vérifier par exemple dans le langage des cocycles.

Enfin, mentionnons qu’il est facile de déduire de ce qui précède comment définir une relation de restriction $H^{2}(K,L)\rightarrow H^{2}(K^{\prime },L)$ pour $L$ un $K$ -lien et $K^{\prime }/K$ une extension.

2.3 Espaces homogènes

Soit $K$ un corps parfait, $G$ un $K$ -groupe algébrique linéaire lisse et $X$ un espace homogène (à droite) de $G$ , à stabilisateurs lisses. On note $x\in X(\bar{K})$ un point géométrique de $X$ , dont on note $\bar{H}$ le stabilisateur.

Une construction due à Springer permet d’associer au couple $(X,x)$ un $K$ -lien $L_{X}=(\bar{H},\unicode[STIX]{x1D705}_{X})$ , ainsi qu’une classe $\unicode[STIX]{x1D702}_{X}\in H^{2}(K,L_{X})$ (on omet abusivement le choix de $x$ dans la suite), tels qu’il existe un morphisme naturel $\unicode[STIX]{x1D70C}:L_{X}\rightarrow \text{}\underline{\text{lien}}(G)$ reliant $\unicode[STIX]{x1D702}_{X}$ à $n(G)$ (cf. [Spr66, Proposition 1.27] ou [Gir71, IV.5.1.3.1]). Rappelons sa construction avec les différents points de vue mentionnés plus haut.

Avec le point de vue de Springer–Borovoi (cf. [Bor93, § 7] ou [FSS98, 5.1]), pour tout $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}$ , il existe $g_{\unicode[STIX]{x1D70E}}\in G(\bar{K})$ tel que $\text{}^{\unicode[STIX]{x1D70E}}x=x\cdot g_{\unicode[STIX]{x1D70E}}$ , et on peut supposer l’application $\unicode[STIX]{x1D70E}\mapsto g_{\unicode[STIX]{x1D70E}}$ continue. Alors, si l’on note $\unicode[STIX]{x1D70E}_{\ast }$ l’automorphisme $\unicode[STIX]{x1D70E}$ -semi-algébrique de $\bar{G}$ induit naturellement par $\unicode[STIX]{x1D70E}$ (cf. [Bor93, 1.4]), on voit que l’automorphisme $\text{Int}\,(g_{\unicode[STIX]{x1D70E}})\circ \unicode[STIX]{x1D70E}_{\ast }$ est aussi $\unicode[STIX]{x1D70E}$ -semi-linéaire mais de plus laisse $\bar{H}$ invariant. On note $f_{\unicode[STIX]{x1D70E}}$ sa restriction à $\bar{H}$ . On a donc une application continue $f:\unicode[STIX]{x1D6E4}_{K}\rightarrow \text{SAut}(\bar{H})$ qui induit un morphisme continu (donc un $K$ -lien) $\unicode[STIX]{x1D705}_{X}:\unicode[STIX]{x1D6E4}_{K}\rightarrow \text{SOut}(\bar{H})$ . On note alors $L_{X}:=(\bar{H},\unicode[STIX]{x1D705}_{X})$ le lien correspondant. On pose enfin  et on vérifie que $\unicode[STIX]{x1D702}_{X}:=[(f,u)]$ est un élément de $H^{2}(K,L_{X})$ ne dépendant pas du choix des $g_{\unicode[STIX]{x1D70E}}$ .

Par construction, on voit que $\unicode[STIX]{x1D702}_{X}$ est neutre si et seulement s’il existe un $K$ -torseur $P$ sous $G$ et un $K$ -morphisme $G$ -équivariant $P\rightarrow X$ .

Avec le point de vue des extensions de groupes (cf. [FSS98, 5.1]), on définit $E_{X}$ comme le sous-groupe de $G(\bar{K})\rtimes \unicode[STIX]{x1D6E4}_{K}$ formé des éléments $(g,\unicode[STIX]{x1D70E})$ tels que $\text{}^{\unicode[STIX]{x1D70E}}x=x\cdot g$ . Alors on dispose d’une suite exacte naturelle de groupes topologiques

$$\begin{eqnarray}1\rightarrow \bar{H}(\bar{K})\rightarrow E_{X}\rightarrow \unicode[STIX]{x1D6E4}_{K}\rightarrow 1,\end{eqnarray}$$

telle que le lien associé est exactement $L_{X}$ et dont la classe dans $H^{2}(K,L_{X})$ est exactement $\unicode[STIX]{x1D702}_{X}$ .

Avec le point de vue de Giraud (cf. [Gir71, IV.5.1]), on peut associer à $X$ la catégorie fibrée ${\mathcal{M}}_{X}$ sur le petit site étale de $\text{Spec}\,K$ des relèvements de $X$ en un torseur sous $G$ , i.e. pour toute $K$ -algèbre étale $A$ , la catégorie fibre ${\mathcal{M}}_{X}(A)$ a pour objets les couples $(P,\unicode[STIX]{x1D6FC})$ où $P\rightarrow \text{Spec}\,A$ est un torseur sous $G$ et $\unicode[STIX]{x1D6FC}:P\rightarrow X_{A}$ est un $A$ -morphisme $G$ -équivariant, et pour morphismes les morphismes de $G$ -torseurs commutant aux morphismes vers $X_{A}$ . Alors ${\mathcal{M}}_{X}$ est une gerbe liée par $L_{X}$ , et sa classe dans $H^{2}(K,L_{X})$ est exactement $\unicode[STIX]{x1D702}_{X}$ . En outre, on dispose d’un morphisme de gerbes naturel $\unicode[STIX]{x1D711}_{X}:{\mathcal{M}}_{X}\rightarrow \text{}\underline{\text{TORS}}(G)$ défini par $(P,\unicode[STIX]{x1D6FC})\mapsto P$ . Pour préciser la fonctorialité ¹ de cette construction, définissons $\text{}\underline{\text{EspHom}}(K)$ comme la catégorie des paires $(G,X)$ où $G$ est un $K$ -groupe algébrique linéaire lisse et $X$ un $K$ -espace homogène de $G$ à stabilisateurs lisses, et $\text{}\underline{\text{GerbesHom}}(K)$ comme la (2-) catégorie des triplets $(G,{\mathcal{M}},\unicode[STIX]{x1D711})$ où $G$ est un $K$ -groupe algébrique linéaire lisse, ${\mathcal{M}}$ une $K$ -gerbe algébrique et $\unicode[STIX]{x1D711}:{\mathcal{M}}\rightarrow \text{}\underline{\text{TORS}}(G)$ un morphisme injectif de $K$ -gerbes. On dispose alors d’un foncteur ‘gerbe de Springer’ :

$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D702}:\text{}\underline{\text{EspHom}}(K) & \rightarrow & \displaystyle \text{}\underline{\text{GerbesHom}}(K)\nonumber\\ \displaystyle (G,X) & \mapsto & \displaystyle (G,{\mathcal{M}}_{X},\unicode[STIX]{x1D711}_{X}).\nonumber\end{eqnarray}$$

3 Gerbes et espaces homogènes de $\text{SL}_{n,K}$

Les résultats suivants sont cruciaux pour la construction géométrique utilisée dans la démonstration du théorème principal. Ils généralisent des outils tout à fait courants dans le cadre où l’on possède un point rationnel, comme le plongement d’un $K$ -groupe affine donné dans $\text{SL}_{n,K}$ , ou le célèbre lemme sans nom, qui établit en particulier la stable birationalité des quotients correspondants à deux tels plongements.

3.1 ‘Plonger une $K$ -gerbe affine dans $\text{SL}_{n,K}$ ’

Soit $K$ un corps parfait et $\bar{K}$ une clôture algébrique de $K$ . Étant donné un $K$ -groupe $G$ , un plongement de $G$ dans $\text{SL}_{n,K}$ permet de construire un espace homogène $X=G\backslash \text{SL}_{n,K}$ muni d’un $K$ -point à stabilisateur $G$ . Inversement, étant donné un espace homogène de $\text{SL}_{n,K}$ muni d’un $K$ -point, on obtient un $K$ -groupe $G$ plongé dans $\text{SL}_{n,K}$ en prenant le stabilisateur du point. Dans cette section on établit une variante de cette équivalence dans le cadre des espaces homogènes sans point rationnel. Un tel espace nous donne toujours une gerbe qui correspond à sa classe de Springer (cf. la section 2.3). Par ‘plonger une $K$ -gerbe dans $\text{SL}_{n,K}$ ’, on veut justement évoquer la construction d’un espace homogène de $\text{SL}_{n,K}$ dont la classe de Springer soit la (classe d’équivalence de la) gerbe que l’on s’est donnée.

On utilise ci-dessous les notations données en section 2.2.

Proposition 3.1. Soit ${\mathcal{M}}$ une $K$ -gerbe algébrique. Alors il existe un entier $n\in \mathbb{N}$ et un morphisme injectif de $K$ -gerbes $\unicode[STIX]{x1D70C}:{\mathcal{M}}\rightarrow \text{}\underline{\text{TORS}}(\text{SL}_{n,K})$ .

Démonstration.

Soit $K^{\prime }/K$ une extension finie galoisienne telle que ${\mathcal{M}}(K^{\prime })\neq \emptyset$ . Choisissons $m\in {\mathcal{M}}(K^{\prime })$ et notons $G^{\prime }:=\text{}\underline{\text{Aut}}(m)$ le $K^{\prime }$ -groupe linéaire associé. On a alors une équivalence de $K^{\prime }$ -gerbes $\unicode[STIX]{x1D711}:{\mathcal{M}}_{K^{\prime }}\xrightarrow[{}]{{\sim}}\text{}\underline{\text{TORS}}(G^{\prime })$ (cf. [Gir71, III.2.5.1]).

Posons $H:=R_{K^{\prime }/K}(G^{\prime })$ . La restriction à la Weil permet alors de définir un morphisme injectif de $K$ -gerbes $\unicode[STIX]{x1D716}:{\mathcal{M}}\rightarrow \text{}\underline{\text{TORS}}(H)$ de la façon suivante : soit $S$ un $K$ -schéma étale. Pour tout $m\in {\mathcal{M}}(S)$ , on note $\unicode[STIX]{x1D716}(m)\in \text{}\underline{\text{TORS}}(H)(S)$ le $S$ -torseur sous $H$ défini par $R_{S_{K^{\prime }}/S}(\unicode[STIX]{x1D711}(m_{K^{\prime }}))$ (par définition, $\unicode[STIX]{x1D711}(m_{K^{\prime }})$ est un $S_{K^{\prime }}$ -torseur sous $G^{\prime }$ ). De même, si $\unicode[STIX]{x1D719}:m\rightarrow m^{\prime }$ est un morphisme dans ${\mathcal{M}}(S)$ , on définit le morphisme $\unicode[STIX]{x1D716}(\unicode[STIX]{x1D719}):\unicode[STIX]{x1D716}(m)\rightarrow \unicode[STIX]{x1D716}(m^{\prime })$ dans $\text{}\underline{\text{TORS}}(H)(S)$ comme le morphisme $R_{S_{K^{\prime }}/S}(\unicode[STIX]{x1D719}_{K^{\prime }}:m_{K^{\prime }}\rightarrow m_{K^{\prime }}^{\prime })$ .

Pour finir, il existe un morphisme injectif de $K$ -groupes affines $j:H\rightarrow \text{SL}_{n,K}$ et on note

$$\begin{eqnarray}\unicode[STIX]{x1D70C}:{\mathcal{M}}\xrightarrow[{}]{\unicode[STIX]{x1D716}}\text{}\underline{\text{TORS}}(H)\xrightarrow[{}]{j}\text{}\underline{\text{TORS}}(\text{SL}_{n,K}),\end{eqnarray}$$

le morphisme composé de $K$ -gerbes.◻

Proposition 3.2. Le foncteur ‘classe de Springer’ $\unicode[STIX]{x1D702}:\text{}\underline{\text{EspHom}}(K)\rightarrow \text{}\underline{\text{GerbesHom}}(K)$ défini dans la section 2.3 est une équivalence de (2-) catégories.

Démonstration.

Construisons un quasi-inverse explicite $\unicode[STIX]{x1D707}:\text{}\underline{\text{GerbesHom}}(K)\rightarrow \text{}\underline{\text{EspHom}}(K)$ . Soit $E:=(G,{\mathcal{M}},\unicode[STIX]{x1D70C})\in \text{}\underline{\text{GerbesHom}}(K)$ . On considère le foncteur $Y_{E}$ qui à tout morphisme étale $S\rightarrow \text{Spec}\,(K)$ associe l’ensemble $Y_{E}(S)$ des couples $(m,\unicode[STIX]{x1D711})$ , avec $m\in {\mathcal{M}}(S)$ et $\unicode[STIX]{x1D711}:\unicode[STIX]{x1D70C}(m)\xrightarrow[{}]{{\sim}}G_{S}$ un morphisme dans $\text{}\underline{\text{TORS}}(G)(S)$ . On dit que deux éléments $(m,\unicode[STIX]{x1D711})$ et $(m^{\prime },\unicode[STIX]{x1D711}^{\prime })$ sont équivalents s’il existe un (iso)morphisme $\unicode[STIX]{x1D713}:m\rightarrow m^{\prime }$ dans ${\mathcal{M}}(S)$ tel que $\unicode[STIX]{x1D711}^{\prime }\circ \unicode[STIX]{x1D70C}(\unicode[STIX]{x1D713})=\unicode[STIX]{x1D711}$ . On définit $X_{E}(S)$ comme le quotient de $Y_{E}(S)$ par cette relation d’équivalence et on note $\overline{(m,\unicode[STIX]{x1D711})}$ la classe d’équivalence de $\unicode[STIX]{x1D711}$ . On définit ainsi un foncteur $X_{E}$ de la catégorie des $K$ -schémas étale vers la catégorie des ensembles. On vérifie facilement que $X_{E}$ est un faisceau étale, admettant des sections localement pour la topologie étale.

On définit une action de $G$ sur $X_{E}$ de la façon suivante : pour tout $S$ étale sur $K$ , pour tout $g\in G(S)$ et $\overline{(m,\unicode[STIX]{x1D711})}\in X_{E}(S)$ , on note $\overline{(m,\unicode[STIX]{x1D711})}\cdot g:=\overline{(m,g\circ \unicode[STIX]{x1D711})}$ , où $g:G_{S}\rightarrow G_{S}$ désigne la translation à gauche par $g$ .

On vérifie que $X_{E}$ est un espace homogène de $G$ (comme faisceau étale). Il est clair que la construction de $X_{E}$ est fonctorielle en $E$ .

Enfin, montrons que $X_{E}$ est représentable par une variété algébrique, i.e. que $(G,X_{E})\in \text{}\underline{\text{EspHom}}(K)$ . Choisissant $x=\overline{(m,\unicode[STIX]{x1D711})}\in X_{E}(K^{\prime })$ , pour une extension finie galoisienne $K^{\prime }$ de $K$ , on note $H^{\prime }:=\text{}\underline{\text{Aut}}(m)$ , qui n’est autre que le stabilisateur de $x$ dans $G_{K^{\prime }}$ . Alors $H^{\prime }$ est un $K^{\prime }$ -groupe linéaire lisse, et $\unicode[STIX]{x1D70C}$ et $\unicode[STIX]{x1D711}$ réalisent $H^{\prime }$ comme un sous-groupe algébrique (fermé) de $G_{K^{\prime }}$ . Alors le morphisme naturel $G_{K^{\prime }}\rightarrow X_{E,K^{\prime }}$ donné par l’action de $G$ sur $x$ induit un isomorphisme $H^{\prime }\backslash G_{K^{\prime }}\xrightarrow[{}]{{\sim}}X_{E,K^{\prime }}$ , ce qui assure que $X_{E,K^{\prime }}$ est représentable par une $K^{\prime }$ -variété quasi-projective. En outre, le choix, pour tout $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}_{K}$ , d’un isomorphisme $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}:\text{}^{\unicode[STIX]{x1D70E}}m\rightarrow m$ dans ${\mathcal{M}}(K^{\prime \prime })$ (avec $K^{\prime \prime }$ extension finie de $K^{\prime }$ ) permet de construire un $2$ -cocycle $(f,u)\in Z^{2}(K,L)$ , où $L$ est le $K$ -lien de ${\mathcal{M}}$ , et une application continue $c:\unicode[STIX]{x1D6E4}_{K}\rightarrow G(\bar{K})$ telle que si $f^{\prime }:\unicode[STIX]{x1D6E4}_{K}\rightarrow \text{SAut}(\bar{G})$ est le morphisme induit par l’action naturelle, on a $f_{\unicode[STIX]{x1D70E}}=\text{Int}\,(c_{\unicode[STIX]{x1D70E}})\circ f_{\unicode[STIX]{x1D70E}}^{\prime }$ et $u_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}}=c_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}f_{\unicode[STIX]{x1D70E}}^{\prime }(c_{\unicode[STIX]{x1D70F}})^{-1}c_{\unicode[STIX]{x1D70E}}^{-1}$ .

On munit alors la $\bar{K}$ -variété quasi-projective $\bar{X}:=\bar{H^{\prime }}\backslash \bar{G}$ , pointée par la classe $x_{0}$ de $\bar{H^{\prime }}$ , de l’action de Galois suivante : pour tout $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}_{K}$ , on pose $\text{}^{\unicode[STIX]{x1D70E}}(x_{0}\cdot g):=x_{0}\cdot (c_{\unicode[STIX]{x1D70E}}f_{\unicode[STIX]{x1D70E}}^{\prime }(g))$ . On vérifie que cela définit bien une action du groupe de Galois de $K$ , et la descente galoisienne (cf. par exemple [BLR90, §6.2, Ex. B]) assure qu’il existe une $K$ -forme $X$ de $\bar{X}$ munie d’une action naturelle de $G$ définie sur $K$ . Enfin, on vérifie que le morphisme précédent $\bar{X}\xrightarrow[{}]{{\sim}}\bar{X}_{E}$ est compatible avec les actions de $\unicode[STIX]{x1D6E4}_{K}$ des deux côtés. Cela assure que $X_{E}$ est représentable (par $X$ ).

On a ainsi défini un foncteur

$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}:\text{}\underline{\text{GerbesHom}}(K) & \rightarrow & \displaystyle \text{}\underline{\text{EspHom}}(K)\nonumber\\ \displaystyle E:=(G,{\mathcal{M}},\unicode[STIX]{x1D70C}) & \mapsto & \displaystyle (G,X_{E}).\nonumber\end{eqnarray}$$

Montrons maintenant que $\unicode[STIX]{x1D702}$ et $\unicode[STIX]{x1D707}$ sont quasi-inverses.

Soit $(G,X)\in \text{}\underline{\text{EspHom}}(K)$ et notons $E_{X}:=(G,{\mathcal{M}}_{X},\unicode[STIX]{x1D70C}_{X})=\unicode[STIX]{x1D702}(X)$ . Pour tout $K$ -schéma étale $S$ , on dispose d’une application canonique $X_{E_{X}}(S)\rightarrow X(S)$ définie par $\overline{(m,\unicode[STIX]{x1D711})}\mapsto \unicode[STIX]{x1D70B}_{m}(\unicode[STIX]{x1D711}^{-1}(1_{G}))$ , où $\unicode[STIX]{x1D70B}_{m}:m\rightarrow X_{S}$ est l’application naturelle. Par construction, cette application est une bijection $G(S)$ -équivariante, fonctorielle en $S$ et $X$ . D’où une transformation naturelle $\unicode[STIX]{x1D707}\circ \unicode[STIX]{x1D702}\rightarrow \text{id}$ .

Soit $E=(G,{\mathcal{M}},\unicode[STIX]{x1D70C})\in \text{}\underline{\text{GerbesHom}}(K)$ et notons $(G,X_{E}):=\unicode[STIX]{x1D707}(E)$ . Pour tout $K$ -schéma étale $S$ , on dispose d’un foncteur naturel ${\mathcal{M}}(S)\rightarrow {\mathcal{M}}_{X_{E}}(S)$ défini sur les objets par $m\mapsto (\unicode[STIX]{x1D71B}_{m}:\text{}\underline{\text{Isom}}_{S}(\unicode[STIX]{x1D70C}(m),G_{S})\rightarrow (X_{E})_{S})$ , avec $\unicode[STIX]{x1D71B}_{m}(\unicode[STIX]{x1D711}):=\overline{(m,\unicode[STIX]{x1D711})}$ . On vérifie que ce foncteur induit une équivalence de $K$ -gerbes ${\mathcal{M}}\rightarrow {\mathcal{M}}_{X_{E}}$ compatible aux morphismes de gerbes $\unicode[STIX]{x1D70C}$ et $\unicode[STIX]{x1D70C}_{X_{E}}$ , fonctorielle en $E$ . D’où une transformation naturelle $\unicode[STIX]{x1D702}\circ \unicode[STIX]{x1D707}\rightarrow \text{id}$ .◻

Corollaire 3.3. Soit ${\mathcal{M}}$ une $K$ -gerbe algébrique. Alors il existe un entier $n$ et un $K$ -espace homogène $X$ de $\text{SL}_{n,K}$ dont la gerbe de Springer ${\mathcal{M}}_{X}$ est isomorphe à ${\mathcal{M}}$ .

Démonstration.

Il suffit d’appliquer la proposition 3.1 et la proposition 3.2.◻

3.2 Le lemme sans nom ni point rationnel

Le lemme sans nom (cf. [CTS07, § 3.2]) permet de montrer que, étant donné un $K$ -groupe algébrique $G$ , tous les espaces homogènes $G\backslash \text{SL}_{n}$ ou $G\backslash \text{GL}_{n}$ (qui possèdent tous des points rationnels) sont $K$ -stablement birationnels entre eux, indépendamment du plongement de $G$ dans ces groupes. Ayant donné un sens au plongement d’une gerbe dans $\text{SL}_{n}$ ou $\text{GL}_{n}$ , on peut maintenant se poser la même question pour des espaces homogènes sans point rationnel, mais ayant la même gerbe associée. Le théorème suivant fournit les outils nécessaires pour répondre affirmativement à cette question, mais aussi pour les constructions géométriques de la preuve du théorème principal.

Théorème 3.4. Soient $G$ un $K$ -groupe linéaire lisse et $X$ un espace homogène de $G$ . Soient $N\subset G$ un sous-groupe distingué et $(G^{\prime },{\mathcal{M}}^{\prime },\unicode[STIX]{x1D70C}^{\prime })\in \text{}\underline{\text{GerbesHom}}(K)$ . On suppose qu’il existe un diagramme commutatif de $K$ -gerbes

avec $\unicode[STIX]{x1D71B}$ surjectif et l’on note $\unicode[STIX]{x1D70C}_{X}^{\prime }:=\unicode[STIX]{x1D70C}^{\prime }\circ \unicode[STIX]{x1D71B}$ .

Alors il existe un $K$ -espace homogène $X^{\prime }$ de $(G/N\times G^{\prime })$ tel que $\unicode[STIX]{x1D702}(X^{\prime })=(G/N\,\times \,G^{\prime },{\mathcal{M}}^{\prime },\unicode[STIX]{x1D70F}\,\times \,\unicode[STIX]{x1D70C}^{\prime })$ , un $K$ -espace homogène $Y$ de $(G\times G^{\prime })$ tel que $\unicode[STIX]{x1D702}(Y)=(G\times G^{\prime },{\mathcal{M}}_{X},\unicode[STIX]{x1D70C}_{X}\times \unicode[STIX]{x1D70C}_{X}^{\prime })$ , et des morphismes naturels de $K$ -espaces homogènes

de sorte que $Y$ est un $X$ -torseur sous $G^{\prime }$ et $Y$ est un $X^{\prime }$ -espace homogène de $N_{X^{\prime }}$ , dont les fibres géométriques ont un stabilisateur isomorphe à $\ker \bar{\unicode[STIX]{x1D71B}}\subset \bar{N}$ , où $\bar{\unicode[STIX]{x1D71B}}$ est un morphisme de $\bar{K}$ -groupes algébriques représentant le morphisme de liens $L({\mathcal{M}}_{X})\rightarrow L({\mathcal{M}}^{\prime })$ liant $\unicode[STIX]{x1D71B}$ .

Remarque.

On appliquera souvent le théorème au cas $G^{\prime }=\text{SL}_{n,K}$ , en utilisant le morphisme $\unicode[STIX]{x1D70C}^{\prime }$ fourni par la proposition 3.1.

Démonstration.

Les hypothèses assurent l’existence du diagramme commutatif de $K$ -gerbes suivant.

On applique alors la proposition 3.2, qui fournit un diagramme de $K$ -espaces homogènes

compatible avec les morphismes naturels de $K$ -groupes algébriques $p_{1}:G\times G^{\prime }\rightarrow G$ et $q_{1}:G\times G^{\prime }\rightarrow G/N\times G$ . Les propriétés de $p$ et $q$ se déduisent par changement de base de $K$ à $\bar{K}$ , oú les gerbes sont trivialisées.◻

On obtient une première application intéressante en posant $G^{\prime }=\text{SL}_{n,K}$ .

Corollaire 3.5 (Le lemme sans nom ni point rationnel).

Soit $G$ un $K$ -groupe algébrique spécial $K$ -rationnel et soit $X$ un espace homogène de $G$ de gerbe de Springer $\unicode[STIX]{x1D70C}_{X}:{\mathcal{M}}_{X}\rightarrow \text{}\underline{\text{TORS}}(G)$ . Alors tout espace homogène $X^{\prime }$ de $\text{SL}_{n,K}$ dont la gerbe de Springer ${\mathcal{M}}_{X^{\prime }}$ est isomorphe à ${\mathcal{M}}_{X}$ (donné par exemple par le corollaire 3.3), est $K$ -stablement birationnel à $X$ .

En particulier, deux espaces homogènes de $\text{SL}_{n,K}$ , dont les gerbes associées sont isomorphes, sont $K$ -stablement birationnels.

Démonstration.

Il suffit d’appliquer le théorème 3.4 à ${\mathcal{M}}^{\prime }:={\mathcal{M}}_{X^{\prime }}$ , $\unicode[STIX]{x1D71B}:{\mathcal{M}}_{X}\rightarrow {\mathcal{M}}_{X^{\prime }}$ un isomorphisme, $\unicode[STIX]{x1D70C}^{\prime }:=\unicode[STIX]{x1D70C}_{X^{\prime }}:{\mathcal{M}}_{X^{\prime }}\rightarrow \text{}\underline{\text{TORS}}(\text{SL}_{n,K})$ , $N=G$ . On obtient alors le diagramme suivant d’espaces homogènes ( $Y$ est un espace homogène de $G\times \text{SL}_{n,K}$ ) :

où $p$ et $q$ sont des torseurs sous $\text{SL}_{n,K}$ et $G$ respectivement. Puisque tous les deux sont des $K$ -groupes spéciaux $K$ -rationnels, on trouve que tant $X$ que $X^{\prime }$ sont $K$ -stablement birationnels à $Y$ , ce qui conclut.◻

Remarques.

(1) Les énoncés des corollaires 3.3 et 3.5 sont valables aussi en remplaçant $\text{SL}_{n,K}$ par $\text{GL}_{n,K}$ .

(2) La proposition 3.1 et le corollaire 3.3 permettent d’associer à toute $K$ -gerbe algébrique une classe d’équivalence birationnelle stable de $K$ -espaces homogènes de groupes spéciaux $K$ -rationnels. De cette façon, toute propriété de ces espaces homogènes invariante par équivalence birationnelle stable peut être vue comme une propriété des gerbes algébriques.

4 ‘L’action d’une gerbe sur un tore’

Dans [LA17], on a donné une petite généralisation du lemme d’Ono au cadre des tores avec une $K$ -action d’un $K$ -groupe fini et lisse. Cela était suffisant pour traiter l’approximation faible pour les espaces homogènes, mais pour traiter le principe de Hasse, il faut généraliser encore un peu cette notion.

Soit donc $K$ un corps parfait et ${\mathcal{M}}$ une $K$ -gerbe algébrique, de lien $L$ . On note $\bar{G}$ le $\bar{K}$ -groupe algébrique sous-jacent à $L$ , et $E$ une extension de $\unicode[STIX]{x1D6E4}_{K}$ par $\bar{G}(\bar{K})$ associée à ${\mathcal{M}}$ . Considérons le morphisme surjectif $\bar{G}\rightarrow \bar{G}^{\text{f}}$ (cf. les notations en début de section 2). Puisque $\bar{G}^{\circ }$ est un sous-groupe caractéristique, ce morphisme induit un $K$ -lien naturel $L^{\text{f}}$ sur $\bar{G}^{\text{f}}$ et un morphisme de liens surjectif $\unicode[STIX]{x1D70B}^{\text{f}}:L\rightarrow L^{\text{f}}$ . On dispose alors de la gerbe ${\mathcal{M}}^{\text{f}}$ comme le poussé en avant (cf. [Gir71, IV.2.3.18]) de ${\mathcal{M}}$ par $\unicode[STIX]{x1D70B}^{\text{f}}:L\rightarrow L^{\text{f}}$ . Elle correspond à l’extension $E^{\text{f}}$ de $\unicode[STIX]{x1D6E4}_{K}$ par $\bar{G}^{\text{f}}(\bar{K})$ (qui est de plus un groupe profini) obtenue à partir de $E$ . On fixe ces données dans toute cette section.

La notion d’‘action d’une gerbe sur un tore’ sera réalisée par l’action de l’extension correspondante selon la définition suivante.

Définition 4.1. On définit un $E$ -tore comme la donnée d’un $\bar{K}$ -tore $\bar{T}$ et d’un homomorphisme continu $\unicode[STIX]{x1D719}:E^{\text{f}}\rightarrow \text{Aut}_{\bar{K}\text{-gr}}(\bar{T})$ .

Un morphisme de $E$ -tores, ou $E$ -morphisme, est un morphisme de $\bar{K}$ -tores compatible avec les actions respectives de $E^{\text{f}}$ . En particulier, on appelera $E$ -isogénie un $E$ -morphisme surjectif et à noyau fini.

L’extension $E^{\text{f}}$ correspond au quotient de $E$ par le sous-groupe distingué $\bar{G}^{\circ }(\bar{K})$ . De la définition ci-dessus on obtient une action naturelle de $E$ sur $\bar{T}$ . D’autre part, on obtient aussi tout naturellement une action de $E$ (via $E^{\text{f}}$ ) sur le module de caractères $\hat{\bar{T}}=\text{Hom}_{\bar{K}}(\bar{T},\mathbb{G}_{\text{m}})$ et il est facile de voir qu’une telle action définit en retour une structure de $E$ -tore sur $\bar{T}$ . On obtient ainsi un foncteur contravariant qui à un $E$ -tore associe son module des caractères.

On dira qu’un $E$ -tore est trivial si l’action de $E^{\text{f}}$ sur $\hat{\bar{T}}$ l’est et quasi-trivial si cette action fait de $\hat{\bar{T}}$ un $E^{\text{f}}$ -module de permutation (notons que tant l’action sur $\hat{\bar{T}}$ que celle sur $\bar{T}$ se factorisent par un quotient fini de $E^{\text{f}}$ par continuité).

On voit facilement aussi que les faits classiques sur les isogénies de tores restent valables dans ce contexte. Notamment, on peut dire que deux $E$ -tores $\bar{T}$ et $\bar{T}^{\prime }$ sont $E$ -isogènes s’il existe une $E$ -isogénie de l’un sur l’autre. L’existence d’une telle isogénie implique en effet immédiatement celle d’une $E$ -isogénie dans l’autre sens.

Notons qu’il y a une façon naturelle d’étendre le morphisme $\unicode[STIX]{x1D719}:E^{\text{f}}\rightarrow \text{Aut}_{\bar{K}}(\bar{T})$ en un morphisme continu $\unicode[STIX]{x1D719}^{\prime }:E^{\text{f}}\rightarrow \text{SAut}(\bar{T})$ . En effet, le groupe $\text{SAut}_{\bar{K}}(\bar{T})$ est canoniquement isomorphe au produit direct $\text{Aut}_{\bar{K}}(\bar{T})\times \unicode[STIX]{x1D6E4}_{K}$ via la $K$ -forme déployée de $\bar{T}$ . Il suffit alors de coupler $\unicode[STIX]{x1D719}$ avec la projection naturelle $E^{\text{f}}\rightarrow \unicode[STIX]{x1D6E4}_{K}$ pour obtenir le morphisme $\unicode[STIX]{x1D719}^{\prime }$ voulu. Ceci nous dit qu’on aurait pu définir un $E$ -tore de façon équivalente comme la donnée d’un $\bar{K}$ -tore $\bar{T}$ et d’un morphisme continu $\unicode[STIX]{x1D719}^{\prime }:E^{\text{f}}\rightarrow \text{SAut}(\bar{T})$ s’insérant dans le carré commutatif suivant.

Au vu de la discussion précédente, cette nouvelle définition est essentiellement équivalente à la précédente, et se prête plus facilement à des généralisations non commutatives.

Remarque.

Ceci est une généralisation de la notion de $K$ -action d’un $K$ -groupe algébrique $G$ sur un $K$ -tore $T$ . En effet, une telle action se factorise toujours par le quotient $G^{\text{f}}$ de $G$ et celle-ci donne de façon naturelle un $E_{G}$ -tore, où $E_{G}$ désigne l’extension naturelle $G(\bar{K})\rtimes \unicode[STIX]{x1D6E4}_{K}$ . L’action de $G^{\text{f}}$ correspond à un morphisme $G^{\text{f}}(\bar{K})\rightarrow \text{Aut}_{\bar{K}}(\bar{T})$ , tandis que la structure de $K$ -groupe de $T$ donne un morphisme continu $\unicode[STIX]{x1D6E4}_{K}\rightarrow \text{Aut}_{\bar{K}}(\bar{T})$ . Le fait que l’action de $G^{\text{f}}$ soit définie sur $K$ permet alors d’étendre naturellement ces deux flèches en un morphisme $G^{\text{f}}(\bar{K})\rtimes \unicode[STIX]{x1D6E4}_{K}\rightarrow \text{Aut}_{\bar{K}}(\bar{T})$ , donnant ainsi un $E_{G^{\text{f}}}$ -tore et donc un $E_{G}$ -tore. On généralise ainsi ce qui a été fait dans [LA17] autour du lemme d’Ono pour traiter les questions d’approximation faible.

Le lemme suivant est une conséquence immédiate de [LA17, Lemma 9] (résultat sur les modules de type fini sans torsion, dû à Ono) et des paragraphes qui précèdent.

Lemme 4.2. Soient $K$ un corps parfait, ${\mathcal{M}}$ une $K$ -gerbe algébrique correspondant à une extension $E$ . Soit $(\bar{T},\unicode[STIX]{x1D719})$ un $E$ -tore et soit $E^{\prime }$ le sous-groupe ouvert de $E^{\text{f}}$ correspondant au noyau de $\unicode[STIX]{x1D719}$ . Alors il existe des $E$ -tores quasi-triviaux $(\bar{P},\unicode[STIX]{x1D719}_{P})$ et $(\bar{Q},\unicode[STIX]{x1D719}_{Q})$ et un entier $r\geqslant 1$ tels que :

• ∙ les morphismes $\unicode[STIX]{x1D719}_{P},\unicode[STIX]{x1D719}_{Q}$ sont triviaux sur $E^{\prime }$ ;

• ∙ le tore $\bar{T}^{r}\times \bar{P}$ est $E$ -isogène à $\bar{Q}$ .

Ce résultat sera utilisé dans la démonstration du théorème principal. En effet, étant donnée une $K$ -gerbe algébrique ${\mathcal{M}}$ associée à une extension $E$ de $\unicode[STIX]{x1D6E4}_{K}$ par $\bar{G}(\bar{K})$ , on construit un $E$ -tore naturel de la façon suivante.

Considérons le morphisme surjectif $\bar{G}\rightarrow \bar{G}^{\text{torf}}$ . Puisque $\bar{G}^{\text{ssu}}$ est aussi un sous-groupe caractéristique, on obtient un $K$ -lien naturel $L^{\text{torf}}$ sur $\bar{G}^{\text{torf}}$ et un morphisme de liens surjectif $\unicode[STIX]{x1D70B}^{\text{torf}}:L\rightarrow L^{\text{torf}}$ qui factorise clairement $\unicode[STIX]{x1D70B}^{\text{f}}$ , ce qui nous permet de définir la gerbe ${\mathcal{M}}^{\text{torf}}$ et l’extension $E^{\text{torf}}$ .

Le tore $\bar{G}^{\text{tor}}$ admet alors naturellement une structure de $E$ -tore. En effet, on dispose de l’extension $E^{\text{torf}}$ :

$$\begin{eqnarray}1\rightarrow \bar{G}^{\text{torf}}(\bar{K})\rightarrow E^{\text{torf}}\rightarrow \unicode[STIX]{x1D6E4}_{K}\rightarrow 1.\end{eqnarray}$$

Puisque $\bar{G}^{\text{tor}}$ est caractéristique dans $\bar{G}^{\text{torf}}$ , on sait que le sous-groupe $\bar{G}^{\text{tor}}(\bar{K})$ est distingué dans $E^{\text{torf}}$ . On en déduit la suite exacte

$$\begin{eqnarray}1\rightarrow \bar{G}^{\text{tor}}(\bar{K})\rightarrow E^{\text{torf}}\rightarrow E^{\text{f}}\rightarrow 1.\end{eqnarray}$$

Le groupe $E^{\text{f}}$ agit alors de façon naturelle sur $\bar{G}^{\text{tor}}(\bar{K})$ et il est facile de voir que cette action se relève en un morphisme continu vers $\text{SAut}(\bar{G}^{\text{tor}})$ , ce qui munit $\bar{G}^{\text{tor}}$ d’une structure de $E$ -tore.

Notons pour finir que cette construction est fonctorielle en $E$ et en $K$ .

5 Énoncé et démonstration du théorème principal

Soit $k$ un corps de nombres. Rappelons que l’on s’intéresse dans cet article à des propriétés arithmétiques comme (BMPH) (cf. la section 1) pour les espaces homogènes des groupes linéaires. Comme il a été dit dans l’introduction, il nous faut cependant un minimum de propriétés d’approximation pour appliquer notre résultat principal. On définit alors l’approximation réelle comme la propriété

(AR) $$\begin{eqnarray}X(k)\neq \emptyset \,\Rightarrow \,\overline{X(k)}=\mathop{\prod }_{v\in \infty _{k}}X(k_{v}),\end{eqnarray}$$

où $\infty _{k}$ représente l’ensemble de places réelles de $k$ . C’est le couple (BMPH) $+$ (AR) qu’il nous faut considérer, afin que la propriété suivante soit vérifiée (nous remercions Olivier Wittenberg pour sa suggestion de présenter ainsi le résultat).

Définition 5.1. Soit $K$ un corps de caractéristique 0 et soit $P$ une propriété des $K$ -variétés. On dit que $P$ est une bonne propriété si elle vérifie, pour $X,Y$ des $K$ -espaces homogènes:

1. (i) si $X$ et $Y$ sont stablement birationnelles, alors $P(X)\Leftrightarrow P(Y)$  ;

2. (ii) si $X\rightarrow Y$ est un morphisme admettant une section, alors $P(X)\Rightarrow P(Y)$  ;

3. (iii) si $X\rightarrow Y$ est un morphisme surjectif dont toute fibre est un espace homogène d’un groupe $G=G^{\text{ssu}}$ avec $G^{\text{ss}}$ simplement connexe, à stabilisateur géométrique $\bar{H}=\bar{H}^{\text{ssu}}$ , alors $P(Y)\Rightarrow P(X)$ .

La justification de cette définition vient du fait que la preuve du résultat principal de [LA17] concernant (BMAF), utilise les trois propriétés ci-dessus (qui sont vérifiées pour (BMAF) ; cf. la proposition 5.3 ci-dessous). Or, la troisième n’est pas vérifiée pour (BMPH), ce qui nous a amenés à rajouter (AR) dans nos hypothèses. Le résultat principal de ce texte est le suivant, et sa preuve est purement géométrique.

Théorème 5.2. Soit $K$ un corps de caractéristique 0, soit $P$ une bonne propriété.

Soit $G$ un $K$ -groupe linéaire connexe, $X$ un espace homogène de $G$ et $x\in X(\bar{K})$ un point à stabilisateur géométrique $\bar{H}$ . Alors, il existe un $\bar{K}$ -groupe fini $\bar{F}$ , extension de $\bar{H}^{\text{f}}$ par un $\bar{K}$ -groupe abélien, un $K$ -espace homogène $X^{\prime }$ de $\text{SL}_{n,K}$ et $x^{\prime }\in X^{\prime }(\bar{K})$ à stabilisateur géométrique $\bar{F}$ tels que $P(X^{\prime })\Rightarrow P(X)$ .

En particulier, si tout espace homogène de $\text{SL}_{n,K}$ à stabilisateurs finis vérifie $P$ , il en va de même pour tout espace homogène d’un groupe linéaire connexe.

La relation entre $X^{\prime }$ et $X$ est même un peu plus forte que celle de l’énoncé. Voir à ce sujet la remarque à la fin du texte.

Remarque.

On peut aussi obtenir un résultat pour des corps parfaits en caractéristique positive si l’on se restreint aux espaces homogènes à stabilisateurs lisses.

Avant de passer à la démonstration du théorème, voyons quelques propriétés arithmétiques qui sont de bonnes propriétés des $k$ -variétés pour $k$ un corps de nombres. La dernière correspond à notre théorème 1.1.

Proposition 5.3. Soit $k$ un corps de nombres. Les propriétés suivantes sont des bonnes propriétés des $k$ -espaces homogènes :

• ∙ le principe de Hasse avec approximation réelle ;

• ∙ l’approximation faible ;

• ∙ l’approximation faible hors de $S$ avec $S$ un ensemble de places non archimédiennes (en particulier l’approximation réelle) ;

• ∙ la propriété (BMPH) $+$ (AR) ;

• ∙ la propriété (BMAF) ;

• ∙ la propriété (BMPH) $+$ (BMAF).

Remarque.

Dans un travail récent [HW18], Harpaz et Wittenberg montrent qu’une variante de la conjecture (E) (i.e. de l’exactitude de la suite (E)) est une bonne propriété des $k$ -espaces homogènes, et que cette variante est vérifiée par les espaces homogènes de $\text{SL}_{n,k}$ à stabilisateurs finis. Les auteurs utilisent alors le théorème 5.2 pour obtenir la conjecture (E) pour tout espace homogène d’un groupe linéaire connexe.

Démonstration.

Pour les espaces homogènes, le fait de posséder un point ou un zéro-cycle de degré 1 (local ou global) est invariant par stable birationalité (utiliser par exemple [Flo06, Théorème 5.7] et le théorème de Lang–Nishimura) et il en va de même pour la densité des points rationnels dans les points locaux. De même, le groupe de Brauer non ramifié $\text{Br}_{\text{nr}}X$ est un invariant birationnel stable et le quotient $\text{Br}_{\text{nr}}X/\text{Br}\,k$ est toujours fini pour ces variétés. Enfin, on sait bien que l’espace affine vérifie l’approximation faible. Ceci donne (i) pour toutes les propriétés de l’énoncé.

Vérifier (ii) est facile pour les propriétés où Brauer–Manin n’intervient pas. La fonctorialité du groupe de Brauer donne les autres par un calcul direct.

Pour (iii), on sait d’après [Bor96, Proposition 3.4] que toute fibre du morphisme $X\rightarrow Y$ sur un point rationnel de $Y$ vérifie le principe de Hasse, l’approximation faible, et possède des points sur toute place finie. On obtient alors chacune des propriétés par la méthode des fibrations.◻

Remarque.

Sur un corps de nombres $k$ admettant une place réelle, la propriété ‘avoir un point rationnel’ n’est pas une bonne propriété des $k$ -variétés.

En revanche, sur un bon corps $K$ de dimension cohomologique ${\leqslant}2$ et de caractéristique nulle (au sens de [BCTS08, § 3.4]), cette propriété est bonne. Le théorème 5.2 pour la propriété ‘avoir un point rationnel’ s’applique par exemple aux corps de nombres totalement imaginaires, aux corps $p$ -adiques, aux corps des fractions d’anneaux intègres strictement henséliens de dimension $2$ et de caractéristique résiduelle nulle.

Preuve du théorème 5.2.

On note $\unicode[STIX]{x1D70C}:{\mathcal{M}}\rightarrow \text{}\underline{\text{TORS}}(G)$ la gerbe de Springer associée à $X$ , $L$ le $K$ -lien de ${\mathcal{M}}$ , $\bar{H}$ le $\bar{K}$ -groupe sous-jacent. On rappelle que l’on dispose des liens naturellement induits $L^{\text{torf}}$ et $L^{\text{f}}$ de groupes respectifs $\bar{H}^{\text{torf}}$ et $\bar{H}^{\text{f}}$ , ainsi que les gerbes correspondantes ${\mathcal{M}}^{\text{torf}}$ et ${\mathcal{M}}^{\text{f}}$ . Enfin, on note $E$ une extension de $\unicode[STIX]{x1D6E4}_{K}$ par $\bar{H}(\bar{K})$ associée à ${\mathcal{M}}$ et $E^{\text{torf}}$ , $E^{\text{f}}$ les extensions induites par les quotients $\bar{H}^{\text{torf}}$ , $\bar{H}^{\text{f}}$ de $\bar{H}$ .

On procède par réductions successives.

Étape 0 : On peut supposer $G^{\text{ss}}$ simplement connexe. En effet, d’après [Bor96, Lemma 5.1], il existe $K$ -un groupe linéaire connexe $G^{\prime }$ avec $(G^{\prime })^{\text{ss}}$ simplement connexe et un morphisme surjectif $G^{\prime }\rightarrow G$ à noyau torique. On peut alors regarder $X$ comme un espace homogène de $G^{\prime }$ , ce qui nous permet de supposer que $G^{\text{ss}}$ est simplement connexe dorénavant. Notons aussi que $\bar{H}^{\text{f}}$ n’a pas été modifié dans le processus.

Étape 1 : Réduction à un espace homogène $X_{1}$ de $G_{1}=G^{\text{tor}}\,\times \,\text{SL}_{n,K}$ avec stabilisateur géométrique $\bar{H}_{1}=\bar{H}^{\text{torf}}$ . Posons $L_{1}:=L^{\text{torf}}$ , $\bar{H}_{1}:=\bar{H}^{\text{torf}}$ et ${\mathcal{M}}_{1}:={\mathcal{M}}^{\text{torf}}$ . Puisque le noyau $L^{\text{ssu}}$ du morphisme $L\rightarrow L_{1}$ est représenté par le $\bar{K}$ -groupe $\bar{H}^{\text{ssu}}$ , qui est caractéristique dans $\bar{H}$ ; et puisque $\bar{H}^{\text{ssu}}$ est contenu dans $\bar{G}^{\text{ssu}}$ , on dispose du diagramme commutatif naturel de $K$ -liens suivant.

On en déduit (cf. [Gir71, IV.2.3.18]) le diagramme commutatif de morphismes de $K$ -gerbes suivant.

En outre, la proposition 3.1 assure qu’il existe un morphisme injectif de $K$ -gerbes $\unicode[STIX]{x1D70C}^{\prime }:{\mathcal{M}}_{1}\rightarrow \text{}\underline{\text{TORS}}(\text{SL}_{n,K})$ . On peut alors appliquer le théorème 3.4 au diagramme précédent et au morphisme $\unicode[STIX]{x1D70C}^{\prime }$ : il existe un $K$ -espace homogène $X_{1}$ de $G_{1}:=G^{\text{tor}}\times \text{SL}_{n,K}$ de gerbe de Springer isomorphe à ${\mathcal{M}}_{1}$ ; un $K$ -espace homogène $Y_{1}$ de $G\times \text{SL}_{n,K}$ de gerbe de Springer ${\mathcal{M}}$ ; et des morphismes naturels de $K$ -espaces homogènes

de sorte que $p$ est un torseur sous $\text{SL}_{n,K}$ et les fibres de $q$ sont des espaces homogènes de $G^{\text{ssu}}$ à stabilisateurs géométriques $\bar{H}^{\text{ssu}}$ .

On voit alors que $Y_{1}$ est $K$ -stablement birationnel à $X$ , ce qui nous dit que $P(Y_{1})\Rightarrow P(X)$ . La description des fibres de $q$ nous permet ensuite de déduire que $P(X_{1})\Rightarrow P(Y_{1})$ , donc on peut se ramener à $X_{1}$ .

Étape 2 : Réduction à un espace homogène $X_{2}$ de $\text{SL}_{n,K}$ à stabilisateur $\bar{H}_{2}$ , extension de $\bar{H}^{\text{f}}$ par un $\bar{K}$ -groupe de type multiplicatif et de gerbe de Springer ${\mathcal{M}}_{2}$ se surjectant naturellement sur ${\mathcal{M}}^{\text{torf}}$ . On rappelle que l’on dispose d’un espace homogène $X_{1}$ de $G_{1}=G^{\text{tor}}\times \text{SL}_{n,K}$ à stabilisateur géométrique $\bar{H}_{1}=\bar{H}^{\text{torf}}$ et de gerbe de Springer ${\mathcal{M}}_{1}={\mathcal{M}}^{\text{torf}}$ .

D’après le lemme d’Ono, il existe un $K$ -tore $R$ et une $K$ -isogénie $Q\rightarrow G^{\text{tor}}\times R$ avec $Q$ un $K$ -tore quasi-trivial. Soit $A$ le noyau fini abélien correspondant et considérons alors le produit $G_{2}^{\prime }:=G_{1}\times R$ et l’isogénie $G_{2}:=\text{SL}_{n,K}\times Q\rightarrow G_{2}^{\prime }$ , de noyau $A$ . La variété $X_{2}^{\prime }:=X_{1}\times R$ est clairement un espace homogène de $G_{2}^{\prime }$ à stabilisateur géométrique $\bar{H}_{1}$ , donc c’est aussi un espace homogène de $G_{2}$ à stabilisateur $\bar{H}_{2}$ , extension de $\bar{H}_{1}$ par $\bar{A}$ . On note ${\mathcal{M}}_{2}^{\prime }$ la gerbe de Springer de  $X_{2}^{\prime }$ .

Or, notons que $\bar{H}_{2}$ est une extension de $\bar{H}^{\text{f}}$ par un $\bar{K}$ -groupe de type multiplicatif. En effet, le noyau de la projection naturelle $\bar{H}_{2}\rightarrow \bar{H}^{\text{f}}$ est une extension de $\bar{H}^{\text{tor}}$ par $\bar{A}$ , qui sont tous les deux de type multiplicatif, le premier étant connexe (cf. [DG70, IV.§ 1, Proposition 4.5]).

Comme la projection $X_{2}^{\prime }\rightarrow X_{1}$ admet une section, on obtient que $P(X_{2}^{\prime })\Rightarrow P(X_{1})$ , donc on peut se réduire au cas de $X_{2}^{\prime }$ . De plus, puisque la projection est équivariante pour le morphisme $G_{2}\rightarrow G_{2}^{\prime }\rightarrow G_{1}$ , on dispose d’un morphisme surjectif naturel de $K$ -gerbes ${\mathcal{M}}_{2}^{\prime }\rightarrow {\mathcal{M}}_{1}={\mathcal{M}}^{\text{torf}}$ .

Enfin, puisque $G_{2}$ est un $K$ -groupe spécial $K$ -rationnel, il suffit d’appliquer le corollaire 3.5 pour se ramener par $K$ -stable birationalité au cas d’un espace homogène $X_{2}$ de $\text{SL}_{n,K}$ à stabilisateur géométrique $\bar{H}_{2}$ . La gerbe de Springer ${\mathcal{M}}_{2}$ de $X_{2}$ est isomorphe à ${\mathcal{M}}_{2}^{\prime }$ .

Étape 3 : Réduction à un espace homogène $X_{3}$ de $\text{SL}_{n,K}$ à stabilisateur géométrique $\bar{H}_{3}$ , extension de $\bar{H}^{\text{f}}$ par un $\bar{K}$ -groupe de type multiplicatif dont la composante neutre est $E^{\text{f}}$ -isogène à un $E^{\text{f}}$ -tore quasi-trivial. On dispose maintenant d’un espace homogène $X_{2}$ de $G_{2}$ , de gerbe ${\mathcal{M}}_{2}$ se surjectant sur ${\mathcal{M}}^{\text{torf}}$ , et à stabilisateur géométrique $\bar{H}_{2}$ , extension de $\bar{H}^{\text{f}}$ par un $\bar{K}$ -groupe de type multiplicatif. En particulier, $\bar{H}_{2}^{\text{f}}$ est une extension de $\bar{H}^{\text{f}}$ par un $\bar{K}$ -groupe fini abélien qui agit trivialement sur $\bar{H}_{2}^{\text{tor}}$ par conjugaison. Donc d’après la construction de la section 4, le tore $\bar{H}_{2}^{\text{tor}}$ possède une structure naturelle de $E^{\text{f}}$ -tore.

Appliquons le lemme 4.2 à $\bar{H}_{2}^{\text{tor}}$ . On obtient un $E^{\text{f}}$ -tore $\bar{R}$ et une $E^{\text{f}}$ -isogénie entre $\bar{R}\times \bar{H}_{2}^{\text{tor}}$ et un $E^{\text{f}}$ -tore quasi-trivial $\bar{Q}$ . Si l’on note $E_{2}$ l’extension de $\unicode[STIX]{x1D6E4}_{K}$ par $\bar{H}_{2}(\bar{K})$ correspondant à ${\mathcal{M}}_{2}$ , on peut alors considérer le produit semi-direct $\bar{R}(\bar{K})\rtimes E_{2}$ . Ce groupe s’insère naturellement dans une suite exacte

$$\begin{eqnarray}1\rightarrow \bar{R}(\bar{K})\rtimes \bar{H}_{2}(\bar{K})\rightarrow \bar{R}(\bar{K})\rtimes E_{2}\rightarrow \unicode[STIX]{x1D6E4}_{K}\rightarrow 1,\end{eqnarray}$$

et on note ${\mathcal{M}}_{3}$ la gerbe associée. Le $\bar{K}$ -groupe $\bar{H}_{3}:=R\rtimes \bar{H}_{2}$ est naturellement extension de $\bar{H}^{\text{f}}$ par un $\bar{K}$ -groupe de type multiplicatif et admet pour composante neutre le $E^{\text{f}}$ -tore $\bar{R}\times \bar{H}_{2}^{\text{tor}}$ , qui est $E^{\text{f}}$ -isogène à $\bar{Q}$ . C’est donc le stabilisateur géométrique souhaité.

Le diagramme commutatif à lignes exactes suivant (avec des flèches $\unicode[STIX]{x1D70E}$ et $\unicode[STIX]{x1D70B}$ définies de façon évidente)

correspond à des morphismes de $K$ -gerbes $\unicode[STIX]{x1D70E}:{\mathcal{M}}_{2}\rightarrow {\mathcal{M}}_{3}$ et $\unicode[STIX]{x1D70B}:{\mathcal{M}}_{3}\rightarrow {\mathcal{M}}_{2}$ tels que $\unicode[STIX]{x1D70B}\circ \unicode[STIX]{x1D70E}=\text{id}$ . En particulier, ${\mathcal{M}}_{3}$ se surjecte sur ${\mathcal{M}}^{\text{f}}$ .

On choisit un morphisme injectif $\unicode[STIX]{x1D704}:{\mathcal{M}}_{3}\rightarrow \text{}\underline{\text{TORS}}(\text{SL}_{n,K})$ comme à la proposition 3.1. Alors la proposition 3.2, appliquée à

assure l’existence d’un espace homogène $X_{2}^{\prime }$ (respectivement $X_{3}$ ) de $\text{SL}_{n,K}$ à stabilisateur géométrique $\bar{H}_{2}$ (respectivement $\bar{H}_{3}$ ) et de gerbe de Springer ${\mathcal{M}}_{2}$ (respectivement ${\mathcal{M}}_{3}$ ), et d’un $K$ -morphisme d’espaces homogènes $X_{2}^{\prime }\rightarrow X_{3}$ . En outre le corollaire 3.5 assure que $X_{2}^{\prime }$ et $X_{2}$ sont stablement birationnels, donc $P(X_{2}^{\prime })\Leftrightarrow P(X_{2})$ .

Notons que l’on dispose désormais du diagramme commutatif de $\bar{K}$ -groupes algébriques suivant.

Considérons maintenant une copie $\text{SL}_{n,K}^{\prime }$ du même groupe $\text{SL}_{n,K}$ avec des copies $s^{\prime }$ et $i^{\prime }$ des plongements de $\bar{H}_{2}$ et de $\bar{R}$ dans $\text{SL}_{n,\bar{K}}^{\prime }$ . On fait agir $\text{SL}_{n,K}$ sur $\text{SL}_{n,K}^{\prime }$ par conjugaison. Le produit semi-direct $\bar{H}_{3}=\bar{R}\rtimes \bar{H}_{2}$ se plonge alors dans le produit semi-direct $G_{3}:=\text{SL}_{n,\bar{K}}^{\prime }\rtimes \text{SL}_{n,K}$ via $i^{\prime }$ et $s$ . En d’autres mots, on a le diagramme commutatif à lignes exactes scindées suivant.

Puisque l’extension $E_{3}$ correspond au produit semi-direct $R\rtimes E_{2}$ et que c’est ainsi qu’on obtient $\unicode[STIX]{x1D70E}:{\mathcal{M}}_{2}\rightarrow {\mathcal{M}}_{3}$ et $\unicode[STIX]{x1D70B}:{\mathcal{M}}_{3}\rightarrow {\mathcal{M}}_{2}$ , on déduit de ce diagramme le diagramme commutatif de $K$ -gerbes suivant.

Par la proposition 3.2, ce diagramme induit un morphisme surjectif d’espaces homogènes $\unicode[STIX]{x1D70B}:X_{3}^{\prime }\rightarrow X_{2}^{\prime }$ , où $X_{3}^{\prime }$ est un $K$ -espace homogène de $G_{3}$ et de gerbe ${\mathcal{M}}_{3}$ . On en déduit aussi que ce morphisme est scindé par un morphisme $\unicode[STIX]{x1D70E}:X_{2}^{\prime }\rightarrow X_{3}^{\prime }$ . Par conséquent, on sait que $P(X_{3}^{\prime })\Rightarrow P(X_{2}^{\prime })$ . En outre, le groupe $G_{3}$ est spécial et $K$ -rationnel, donc le corollaire 3.5 assure que $X_{3}^{\prime }$ est stablement birationnel à l’espace homogène $X_{3}$ de $\text{SL}_{n,K}$ dont la gerbe est ${\mathcal{M}}_{3}$ , donc $P(X_{3}^{\prime })\Leftrightarrow P(X_{3})$ .

Finalement, on a bien $P(X_{3})\Rightarrow P(X_{2})$ , donc on s’est ramené à un espace homogène $X_{3}$ de $\text{SL}_{n,K}$ à stabilisateur $\bar{H}_{3}$ et gerbe de Springer ${\mathcal{M}}_{3}$ se surjectant sur ${\mathcal{M}}^{\text{f}}$ .

Étape 4 : Réduction à un espace homogène $X_{4}$ de $\text{SL}_{n,K}$ à stabilisateur géométrique $\bar{H}_{4}$ , extension de $\bar{H}^{\text{f}}$ par un $\bar{K}$ -groupe fini abélien. On rappelle que l’on dispose d’un espace homogène $X_{3}$ de gerbe ${\mathcal{M}}_{3}$ se surjectant sur ${\mathcal{M}}^{\text{f}}$ , et dont le stabilisateur géométrique $\bar{H}_{3}$ est extension de $\bar{H}^{\text{f}}$ par un groupe de type multiplicatif dont la composante neutre $\bar{H}_{3}^{\text{tor}}$ est un $E^{\text{f}}$ -tore $E^{\text{f}}$ -isogène à un $E^{\text{f}}$ -tore quasi-trivial $\bar{Q}$ . Rappelons que $E_{3}$ (respectivement  $E_{3}^{\text{f}}$ ) est une extension de $\unicode[STIX]{x1D6E4}_{K}$ par $\bar{H}_{3}(\bar{K})$ (respectivement  $\bar{H}_{3}^{\text{f}}$ ) définissant ${\mathcal{M}}_{3}$ (respectivement  ${\mathcal{M}}_{3}^{\text{f}}$ ). La construction du $E_{3}$ -tore $\bar{H}_{3}^{\text{tor}}$ (cf. la section 4) nous fournit la suite exacte

$$\begin{eqnarray}1\rightarrow \bar{H}_{3}^{\text{tor}}(\bar{K})\rightarrow E_{3}\rightarrow E_{3}^{\text{f}}\rightarrow 1.\end{eqnarray}$$

Puisque $E_{3}^{\text{f}}$ est un groupe profini, cette extension correspond à une classe $\unicode[STIX]{x1D701}\in H^{2}(E_{3}^{\text{f}},\bar{H}_{3}^{\text{tor}}(\bar{K}))$ . Or ce groupe est de torsion (car $E_{3}^{\text{f}}$ est profini), donc il existe un entier $m\geqslant 1$ tel que $m\unicode[STIX]{x1D701}=0$ . Cela veut dire que, si l’on note par $\bar{A}^{\prime }$ le $\bar{K}$ -sous-groupe de $m$ -torsion de $\bar{H}_{3}^{\text{tor}}$ , la suite exacte longue de cohomologie nous permet de déduire que l’extension ci-dessus provient d’une extension de $E_{3}^{\text{f}}$ par $\bar{A}^{\prime }(\bar{K})$ . Autrement dit, on a le diagramme commutatif à lignes exactes suivant.

On définit alors $\bar{A}$ comme le noyau du morphisme composé de $E^{\text{f}}$ -tores

$$\begin{eqnarray}\unicode[STIX]{x1D70C}:\bar{H}_{3}^{\text{tor}}\xrightarrow[{}]{\times m}\bar{H}_{3}^{\text{tor}}\rightarrow \bar{Q}.\end{eqnarray}$$

Puisque $\bar{A}^{\prime }\subset \bar{A}\subset \bar{H}_{3}^{\text{tor}}$ , l’extension $E_{4}^{\prime }$ induit une extension $E_{4}$ de $E_{3}^{\text{f}}$ par $\bar{A}(\bar{K})$ qui factorise le diagramme précédent. Or, on dispose d’un morphisme naturel $E_{4}\rightarrow \unicode[STIX]{x1D6E4}_{K}$ via son quotient $E_{3}^{\text{f}}$ et l’on définit alors $\bar{H}_{4}$ comme le $\bar{K}$ -groupe fini correspondant au noyau (abstrait) de ce morphisme. On obtient alors la suite exacte supérieure dans le diagramme commutatif suivant.

On interprète ce dernier diagramme comme un morphisme injectif de $K$ -gerbes ${\mathcal{M}}_{4}\rightarrow {\mathcal{M}}_{3}$ . En utilisant le morphisme injectif ${\mathcal{M}}_{3}\rightarrow \text{}\underline{\text{TORS}}(\text{SL}_{n,K})$ donné par l’espace homogène $X_{3}$ , la proposition 3.2 assure donc l’existence d’un espace homogène $X_{4}$ de $\text{SL}_{n,K}$ de gerbe ${\mathcal{M}}_{4}$ , donc de stabilisateur géométrique $\bar{H}_{4}$ , muni d’un morphisme surjectif $X_{4}\rightarrow X_{3}$ équivariant pour les actions de $\text{SL}_{n,K}$ .

Notons enfin que le groupe $\bar{H}_{4}$ est une extension $\bar{H}^{\text{f}}$ par un $\bar{K}$ -groupe abélien. En effet, le noyau du morphisme composé $\bar{H}_{4}\rightarrow \bar{H}_{3}\rightarrow \bar{H}^{\text{f}}$ est contenu dans un $\bar{K}$ -groupe de type multiplicatif par construction de $\bar{H}_{3}$ . Et le morphisme est clairement surjectif car $\bar{H}_{4}$ se surjecte sur $\bar{H}_{3}^{\text{f}}$ par construction.

On affirme que l’espace $X_{4}$ est $K$ -stablement birationnel à $X_{3}$ , ce qui suffit pour conclure la démonstration du théorème puisqu’alors $P(X_{4})\Leftrightarrow P(X_{3})$ . Pour démontrer cela, il suffira de démontrer que, si l’on note $\unicode[STIX]{x1D709}$ le point générique de $X_{3}$ et $K(\unicode[STIX]{x1D709})$ le corps de fonctions correspondant, alors la fibre générique $X_{4,\unicode[STIX]{x1D709}}$ est $K(\unicode[STIX]{x1D709})$ -rationnelle.

Le point générique $\unicode[STIX]{x1D709}$ de $X_{3}$ nous donne une $K(\unicode[STIX]{x1D709})$ -forme naturelle $H_{3,\unicode[STIX]{x1D709}}$ de $\bar{H}_{3}$ et donc une $K(\unicode[STIX]{x1D709})$ -forme $H_{3,\unicode[STIX]{x1D709}}^{\text{f}}$ de $\bar{H}_{3}^{\text{f}}$ . On en déduit une section $\unicode[STIX]{x1D6E4}_{K(\unicode[STIX]{x1D709})}\rightarrow E_{3,\unicode[STIX]{x1D709}}^{\text{f}}$ de l’extension associée à ${\mathcal{M}}_{3,\unicode[STIX]{x1D709}}^{\text{f}}$ qui définit l’action de $\unicode[STIX]{x1D6E4}_{K(\unicode[STIX]{x1D709})}$ sur $\bar{H}_{3}^{\text{f}}$ . Or $E^{\text{f}}$ est un quotient de $E_{3}^{\text{f}}$ dont le noyau correspond au noyau de la projection $\bar{H}_{3}^{\text{f}}\rightarrow \bar{H}^{\text{f}}$ . Donc ce noyau est stable par l’action de $E_{3}^{\text{f}}$ par conjugaison, et donc stable par l’action de $E_{3,\unicode[STIX]{x1D709}}^{\text{f}}$ et par celle de $\unicode[STIX]{x1D6E4}_{K(\unicode[STIX]{x1D709})}$ . En d’autres mots, ce noyau est un $K(\unicode[STIX]{x1D709})$ -sous-groupe distingué de $H_{3,\unicode[STIX]{x1D709}}^{\text{f}}$ et l’on obtient ainsi une $K(\unicode[STIX]{x1D709})$ -forme $H_{\unicode[STIX]{x1D709}}^{\text{f}}$ de $\bar{H}^{\text{f}}$ . La $K(\unicode[STIX]{x1D709})$ -gerbe ${\mathcal{M}}_{\unicode[STIX]{x1D709}}^{\text{f}}$ est donc isomorphe à $\text{}\underline{\text{TORS}}(H_{\unicode[STIX]{x1D709}}^{\text{f}})$ et on obtient une section $s_{\unicode[STIX]{x1D709}}:\unicode[STIX]{x1D6E4}_{K(\unicode[STIX]{x1D709})}\rightarrow E_{\unicode[STIX]{x1D709}}^{\text{f}}$ de l’extension correspondant à ${\mathcal{M}}_{\unicode[STIX]{x1D709}}^{\text{f}}$ .

Notons en outre que la fonctorialité de la construction des $E^{\text{f}}$ -tores fait de tout $E^{\text{f}}$ -tore un $E_{\unicode[STIX]{x1D709}}^{\text{f}}$ -tore (via la projection $E_{\unicode[STIX]{x1D709}}^{\text{f}}\rightarrow E^{\text{f}}$ ). En particulier, puisque l’on dispose de la section $s_{\unicode[STIX]{x1D709}}$ de $E_{\unicode[STIX]{x1D709}}^{\text{f}}$ , tout $E^{\text{f}}$ -tore admet une $K(\unicode[STIX]{x1D709})$ -forme naturelle (pour $\bar{H}_{3}^{\text{tor}}$ , c’est justement $H_{3,\unicode[STIX]{x1D709}}^{\text{tor}}$ ). On en déduit que $\bar{Q}$ admet une $K(\unicode[STIX]{x1D709})$ -forme $Q_{\unicode[STIX]{x1D709}}$ qui est quasi-triviale en tant que $K(\unicode[STIX]{x1D709})$ -tore et le morphisme $\unicode[STIX]{x1D70C}:H_{3,\unicode[STIX]{x1D709}}^{\text{tor}}\rightarrow Q_{\unicode[STIX]{x1D709}}$ est alors un $K(\unicode[STIX]{x1D709})$ -morphisme. D’où une $K(\unicode[STIX]{x1D709})$ -forme naturelle $A_{\unicode[STIX]{x1D709}}$ de $\bar{A}$ et une suite exacte de $K(\unicode[STIX]{x1D709})$ -groupes abéliens

$$\begin{eqnarray}1\rightarrow A_{\unicode[STIX]{x1D709}}\rightarrow H_{3,\unicode[STIX]{x1D709}}^{\text{tor}}\xrightarrow[{}]{\unicode[STIX]{x1D70C}}Q_{\unicode[STIX]{x1D709}}\rightarrow 1.\end{eqnarray}$$

Or la variété $X_{4,\unicode[STIX]{x1D709}}$ correspond à la fibre du morphisme $X_{4,K(\unicode[STIX]{x1D709})}\rightarrow X_{3,K(\unicode[STIX]{x1D709})}$ au $K(\unicode[STIX]{x1D709})$ -point $\unicode[STIX]{x1D709}$ . Le groupe $\text{SL}_{n,K(\unicode[STIX]{x1D709})}$ agit sur les deux variétés de façon compatible, donc le groupe $H_{3,\unicode[STIX]{x1D709}}$ le fait aussi en tant que sous- $K(\unicode[STIX]{x1D709})$ -groupe de $\text{SL}_{n,K(\unicode[STIX]{x1D709})}$ . Mais puisque ce sous-groupe fixe le point $\unicode[STIX]{x1D709}$ , il agit naturellement par restriction sur la fibre $X_{4,\unicode[STIX]{x1D709}}$ . Cette action est transitive sur $\overline{K(\unicode[STIX]{x1D709})}$ et a pour stabilisateur $\bar{H}_{4,\overline{K(\unicode[STIX]{x1D709})}}$ . Le tore $H_{3,\unicode[STIX]{x1D709}}^{\text{tor}}$ agit alors sur $X_{4,\unicode[STIX]{x1D709}}$ par restriction et l’on vérifie aisément que cette action est aussi transitive sur $\overline{K(\unicode[STIX]{x1D709})}$ puisque $\bar{H}_{4,\overline{K(\unicode[STIX]{x1D709})}}$ rencontre toutes les composantes connexes de $H_{3,\overline{K(\unicode[STIX]{x1D709})}}$ . Le stabilisateur géométrique de cette action est clairement $H_{3,\overline{K(\unicode[STIX]{x1D709})}}^{\text{tor}}\cap \bar{H}_{4,\overline{K(\unicode[STIX]{x1D709})}}=\bar{A}_{\overline{K(\unicode[STIX]{x1D709})}}$ , qui est défini sur $K(\unicode[STIX]{x1D709})$ comme on l’a déjà démontré. La variété $X_{4,\unicode[STIX]{x1D709}}$ est alors un torseur sous le $K(\unicode[STIX]{x1D709})$ -groupe quotient $H_{3,\unicode[STIX]{x1D709}}^{\text{tor}}/A_{\unicode[STIX]{x1D709}}=Q_{\unicode[STIX]{x1D709}}$ . Or ce tore est quasi-trivial, donc $K(\unicode[STIX]{x1D709})$ -rationnel, et $H^{1}(K(\unicode[STIX]{x1D709}),Q_{\unicode[STIX]{x1D709}})=0$ . Par conséquent, $X_{4,\unicode[STIX]{x1D709}}$ est isomorphe à $Q_{\unicode[STIX]{x1D709}}$ , et donc est $K(\unicode[STIX]{x1D709})$ -rationnelle.

En posant $\bar{F}=\bar{H}_{4}$ et $X^{\prime }=X_{4}$ , ceci conclut la preuve du théorème.◻

Remarque.

En suivant la preuve, on peut constater que non seulement $\bar{F}$ est une extension de $\bar{H}^{\text{f}}$ par un $\bar{K}$ -groupe abélien, mais en fait on a un morphisme naturel et surjectif de $K$ -liens $L_{X^{\prime }}\rightarrow L^{\text{f}}$ qui envoie ${\mathcal{M}}_{X^{\prime }}$ en ${\mathcal{M}}^{\text{f}}$ . De plus, lorsque $X$ possède un $K$ -point, il est facile de voir que cette construction fournit un espace homogène $X^{\prime }$ qui possède aussi un $K$ -point et le morphisme $\bar{F}\rightarrow \bar{H}^{\text{f}}$ est alors défini sur $K$ (une autre façon de se convaincre de ce fait est de suivre la preuve dans [LA17]). Ce fait devrait être utile pour obtenir des résultats inconditionnels sur (BMPH) pour des stabilisateurs non connexes à partir de résultats positifs pour des stabilisateurs finis, suivant l’exemple de [LA17, § 5].