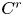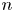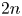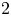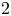1. Introduction
Haefliger defined the notion of ![]() $C^r$-Haefliger structures on manifolds which are more flexible than
$C^r$-Haefliger structures on manifolds which are more flexible than ![]() $C^r$-foliations to be able to construct a classifying space
$C^r$-foliations to be able to construct a classifying space ![]() $\mathrm {B}\Gamma ^{r}_n$ for them [Reference HaefligerHae71, Reference BottBot72]. This space is the classifying space of the étale groupoid
$\mathrm {B}\Gamma ^{r}_n$ for them [Reference HaefligerHae71, Reference BottBot72]. This space is the classifying space of the étale groupoid ![]() $\Gamma _n$ of germs of local
$\Gamma _n$ of germs of local ![]() $C^r$-diffeomorphisms of
$C^r$-diffeomorphisms of ![]() $\mathbb {R}^n$. For
$\mathbb {R}^n$. For ![]() $r>0$, there is a map
$r>0$, there is a map
which classifies the normal bundle to the ![]() $C^r$-Haefliger structures and the homotopy fiber of
$C^r$-Haefliger structures and the homotopy fiber of ![]() $\nu$ is denoted by
$\nu$ is denoted by ![]() $\overline {\mathrm {B}\Gamma }^{r}_n$.
$\overline {\mathrm {B}\Gamma }^{r}_n$.
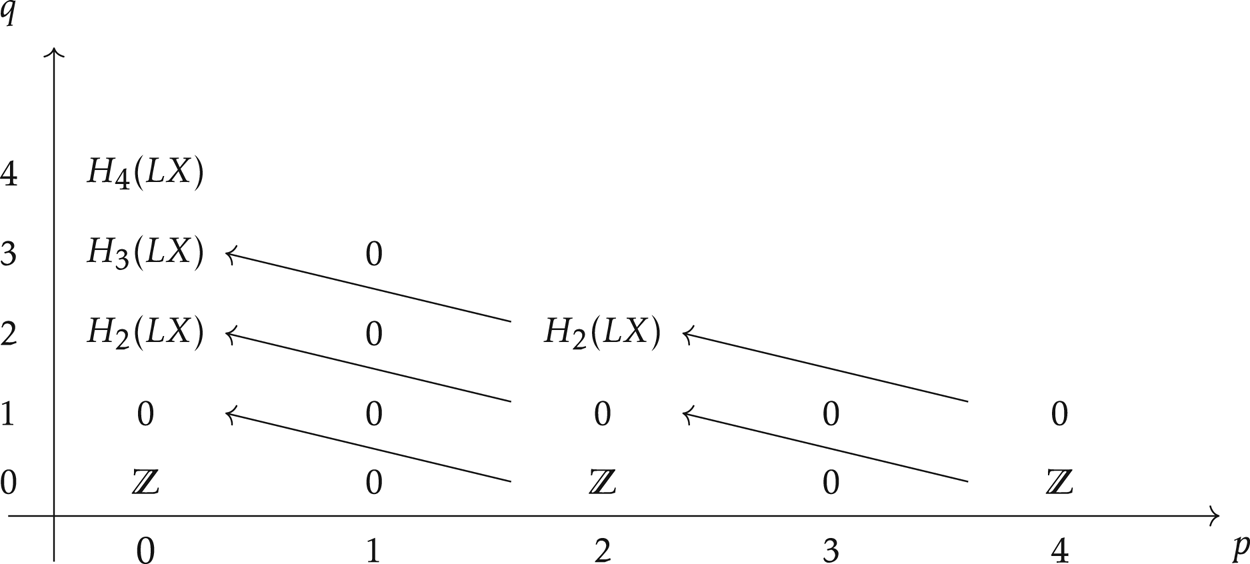
Figure 1. The second page of the Serre spectral sequence for the fibration ![]() $LX\to LX/\!\!/ S^1\to \mathrm {B}S^1$.
$LX\to LX/\!\!/ S^1\to \mathrm {B}S^1$.
The work of Haefliger [Reference HaefligerHae71] and Thurston's h-principle theorems [Reference ThurstonThu74b, Reference ThurstonThu76] say that if the normal bundle of a ![]() $C^r$-Haefliger structure
$C^r$-Haefliger structure ![]() $\gamma$ on a manifold
$\gamma$ on a manifold ![]() $M$ can be embedded into the tangent bundle
$M$ can be embedded into the tangent bundle ![]() $TM$, then there is a genuine foliation in the homotopy class of
$TM$, then there is a genuine foliation in the homotopy class of ![]() $\gamma$. Hence, in principle, the classification of foliations on
$\gamma$. Hence, in principle, the classification of foliations on ![]() $M$ is translated into the homotopy type of the mysterious space
$M$ is translated into the homotopy type of the mysterious space ![]() $\overline {\mathrm {B}\Gamma }^{r}_n$. Haefliger proved that
$\overline {\mathrm {B}\Gamma }^{r}_n$. Haefliger proved that ![]() $\overline {\mathrm {B}\Gamma }^{r}_n$ is
$\overline {\mathrm {B}\Gamma }^{r}_n$ is ![]() $n$-connected and Thurston proved [Reference ThurstonThu74a] that the identity component of the smooth diffeomorphism group of any compact manifold is a simple group and used it to show that
$n$-connected and Thurston proved [Reference ThurstonThu74a] that the identity component of the smooth diffeomorphism group of any compact manifold is a simple group and used it to show that ![]() $\overline {\mathrm {B}\Gamma }^{\infty }_n$ is
$\overline {\mathrm {B}\Gamma }^{\infty }_n$ is ![]() $(n+1)$-connected; shortly after, Mather [Reference MatherMat74, § 7] proved the same statement for
$(n+1)$-connected; shortly after, Mather [Reference MatherMat74, § 7] proved the same statement for ![]() $\overline {\mathrm {B}\Gamma }^{r}_n$ for all regularities
$\overline {\mathrm {B}\Gamma }^{r}_n$ for all regularities ![]() $r$ except
$r$ except ![]() $r=n+1$.
$r=n+1$.
The theory of differentiable cohomology for groupoids developed by Haefliger made him speculate that ![]() $\overline {\mathrm {B}\Gamma }^{r}_n$ might be
$\overline {\mathrm {B}\Gamma }^{r}_n$ might be ![]() $2n$-connected, and Thurston also stated [Reference ThurstonThu74a] this range of connectivity for
$2n$-connected, and Thurston also stated [Reference ThurstonThu74a] this range of connectivity for ![]() $\overline {\mathrm {B}\Gamma }^r_n$ as a conjecture.
$\overline {\mathrm {B}\Gamma }^r_n$ as a conjecture.
Conjecture 1.1 (Haefliger–Thurston)
The space ![]() $\overline {\mathrm {B}\Gamma }^r_n$ is
$\overline {\mathrm {B}\Gamma }^r_n$ is ![]() $2n$-connected.
$2n$-connected.
A geometric consequence of this conjecture [Reference ThurstonThu74b, Reference ThurstonThu76] is that any subbundle of the tangent bundle of a smooth ![]() $M$ whose dimension is at most
$M$ whose dimension is at most ![]() $(\mathrm {dim}(M)+1)/2$ is
$(\mathrm {dim}(M)+1)/2$ is ![]() $C^r$-integrable up to homotopy, that is, one can change it up to homotopy to become the tangent field of a
$C^r$-integrable up to homotopy, that is, one can change it up to homotopy to become the tangent field of a ![]() $C^r$-foliation on
$C^r$-foliation on ![]() $M$. As a consequence of Mather's acyclicity result [Reference MatherMat71] and McDuff's theorem [Reference McDuffMcD80], we know that
$M$. As a consequence of Mather's acyclicity result [Reference MatherMat71] and McDuff's theorem [Reference McDuffMcD80], we know that ![]() $\overline {\mathrm {B}\Gamma }^0_n$ is contractible, and it is a consequence of the remarkable theorem of Tsuboi [Reference TsuboiTsu89] that
$\overline {\mathrm {B}\Gamma }^0_n$ is contractible, and it is a consequence of the remarkable theorem of Tsuboi [Reference TsuboiTsu89] that ![]() $\overline {\mathrm {B}\Gamma }^1_n$ is also contractible. But for regularity
$\overline {\mathrm {B}\Gamma }^1_n$ is also contractible. But for regularity ![]() $r>1$, because of the existence and nontriviality of Godbillon–Vey invariants, it is known that
$r>1$, because of the existence and nontriviality of Godbillon–Vey invariants, it is known that ![]() $\overline {\mathrm {B}\Gamma }^r_n$ is not
$\overline {\mathrm {B}\Gamma }^r_n$ is not ![]() $(2n+1)$-connected.
$(2n+1)$-connected.
In this paper, we consider the piecewise linear (PL) category instead and we prove the analog of this conjecture for PL foliations of codimension ![]() $2$. To formulate the conjecture in this category, we shall first define
$2$. To formulate the conjecture in this category, we shall first define ![]() $\overline {\mathrm {B}\Gamma }_n^{\mathrm {PL}}$. Let
$\overline {\mathrm {B}\Gamma }_n^{\mathrm {PL}}$. Let ![]() $\Gamma _n^{\mathrm {PL}}$ be the étale groupoid of germs of local orientation-preserving PL homeomorphisms of
$\Gamma _n^{\mathrm {PL}}$ be the étale groupoid of germs of local orientation-preserving PL homeomorphisms of ![]() $\mathbb {R}^n$. The classifying space
$\mathbb {R}^n$. The classifying space ![]() $\mathrm {B}\Gamma _n^{\mathrm {PL}}$ classifies codimension
$\mathrm {B}\Gamma _n^{\mathrm {PL}}$ classifies codimension ![]() $n$ PL Haefliger structures that are co-oriented up to concordance [Reference HaefligerHae71, § 2]. Another perspective is that it classifies foliated PL microbundles of dimension
$n$ PL Haefliger structures that are co-oriented up to concordance [Reference HaefligerHae71, § 2]. Another perspective is that it classifies foliated PL microbundles of dimension ![]() $n$ [Reference HaefligerHae70, p. 188, Proposition] or [Reference TsuboiTsu09, § 4]. On the other hand, the Kuiper–Lashof theorem implies that oriented PL microbundles of dimension
$n$ [Reference HaefligerHae70, p. 188, Proposition] or [Reference TsuboiTsu09, § 4]. On the other hand, the Kuiper–Lashof theorem implies that oriented PL microbundles of dimension ![]() $n$ are classified by
$n$ are classified by ![]() $\mathrm {B}\mathrm {PL}^+(\mathbb {R}^n)$, where
$\mathrm {B}\mathrm {PL}^+(\mathbb {R}^n)$, where ![]() $\mathrm {PL}^+(\mathbb {R}^n)$ is the realization of the simplicial group of orientation-preserving PL homeomorphisms of
$\mathrm {PL}^+(\mathbb {R}^n)$ is the realization of the simplicial group of orientation-preserving PL homeomorphisms of ![]() $\mathbb {R}^n$ [Reference Kuiper and LashofKL66]. So forgetting the germ of the foliation near the zero section of microbundles induces a map
$\mathbb {R}^n$ [Reference Kuiper and LashofKL66]. So forgetting the germ of the foliation near the zero section of microbundles induces a map
This map classifies the normal microbundle of the PL Haefliger structures. Let ![]() $\overline {\mathrm {B}\Gamma }_n^{\mathrm {PL}}$ be the homotopy fiber of the above map
$\overline {\mathrm {B}\Gamma }_n^{\mathrm {PL}}$ be the homotopy fiber of the above map ![]() $\nu$. Haefliger's argument [Reference HaefligerHae71, § 6] implies that
$\nu$. Haefliger's argument [Reference HaefligerHae71, § 6] implies that ![]() $\overline {\mathrm {B}\Gamma }_n^{\mathrm {PL}}$ is
$\overline {\mathrm {B}\Gamma }_n^{\mathrm {PL}}$ is ![]() $(n-1)$-connected. He proved in [Reference HaefligerHae70, Theorem 3] that Phillips’ submersion theorem in the smooth category implies that
$(n-1)$-connected. He proved in [Reference HaefligerHae70, Theorem 3] that Phillips’ submersion theorem in the smooth category implies that ![]() $\overline{\mathrm {B}\Gamma}_n^r$ is
$\overline{\mathrm {B}\Gamma}_n^r$ is ![]() $n$-connected for
$n$-connected for ![]() $r>0$. Given that Phillips’ submersion theorem also holds in the PL category [Reference Haefliger and PoenaruHP64], one could argue similarly to the smooth case to show that
$r>0$. Given that Phillips’ submersion theorem also holds in the PL category [Reference Haefliger and PoenaruHP64], one could argue similarly to the smooth case to show that ![]() $\overline {\mathrm {B}\Gamma }_n^{\mathrm {PL}}$ is in fact
$\overline {\mathrm {B}\Gamma }_n^{\mathrm {PL}}$ is in fact ![]() $n$-connected. The analog of the Haefliger–Thurston conjecture in the PL category is that the classifying space
$n$-connected. The analog of the Haefliger–Thurston conjecture in the PL category is that the classifying space ![]() $\overline {\mathrm {B}\Gamma }_n^{\mathrm {PL}}$ is
$\overline {\mathrm {B}\Gamma }_n^{\mathrm {PL}}$ is ![]() $2n$-connected. Unlike the smooth case, it is not even known whether
$2n$-connected. Unlike the smooth case, it is not even known whether ![]() $\overline {\mathrm {B}\Gamma }_n^{\mathrm {PL}}$ is
$\overline {\mathrm {B}\Gamma }_n^{\mathrm {PL}}$ is ![]() $(n+1)$-connected for all
$(n+1)$-connected for all ![]() $n$. Our main theorem is about the connectivity of this space for
$n$. Our main theorem is about the connectivity of this space for ![]() $n=2$.
$n=2$.
Theorem 1.2 The space ![]() $\overline {\mathrm {B}\Gamma }_2^{\mathrm {PL}}$ is
$\overline {\mathrm {B}\Gamma }_2^{\mathrm {PL}}$ is ![]() $4$-connected.
$4$-connected.
As a consequence of this theorem, we prove new homological properties of PL surface homeomorphisms.
1.1 Applications
Let ![]() $M$ be a compact connected PL
$M$ be a compact connected PL ![]() $n$-manifold possibly with nonempty boundary. Let
$n$-manifold possibly with nonempty boundary. Let ![]() $\mathrm {PL}(M, \mathrm {rel}\,\partial )$ be the group of PL homeomorphisms of
$\mathrm {PL}(M, \mathrm {rel}\,\partial )$ be the group of PL homeomorphisms of ![]() $M$ which agree with the identity on an open neighborhood of the boundary and let
$M$ which agree with the identity on an open neighborhood of the boundary and let ![]() $\mathrm {PL}_{0}(M, \mathrm {rel}\,\partial )$ be the identity component of
$\mathrm {PL}_{0}(M, \mathrm {rel}\,\partial )$ be the identity component of ![]() $\mathrm {PL}(M, \mathrm {rel}\,\partial )$. Epstein [Reference EpsteinEps70, Theorem 3.1] considered the abstract group
$\mathrm {PL}(M, \mathrm {rel}\,\partial )$. Epstein [Reference EpsteinEps70, Theorem 3.1] considered the abstract group ![]() $G={{\mathrm {PL}}}^{\delta }_{0}(M, \mathrm {rel}\,\partial )$ and showed that the commutator subgroup
$G={{\mathrm {PL}}}^{\delta }_{0}(M, \mathrm {rel}\,\partial )$ and showed that the commutator subgroup ![]() $[G,G]$ is a simple group. Hence, to prove that
$[G,G]$ is a simple group. Hence, to prove that ![]() $G$ is simple, it is enough to show that it is perfect. He then proved that
$G$ is simple, it is enough to show that it is perfect. He then proved that ![]() $\mathrm {PL}([0,1], \mathrm {rel}\,\partial )$ and
$\mathrm {PL}([0,1], \mathrm {rel}\,\partial )$ and ![]() $\mathrm {PL}_0(S^1)$ are perfect by observing that in dimension
$\mathrm {PL}_0(S^1)$ are perfect by observing that in dimension ![]() $1$, PL homeomorphisms are generated by certain ‘typical elements’ and those typical elements can be easily written as commutators. To generalize his argument to higher dimensions, he suggested the following approach [Reference EpsteinEps70, p. 173].
$1$, PL homeomorphisms are generated by certain ‘typical elements’ and those typical elements can be easily written as commutators. To generalize his argument to higher dimensions, he suggested the following approach [Reference EpsteinEps70, p. 173].
Definition 1.3 Let ![]() $B$ be a ball in
$B$ be a ball in ![]() $\mathbb {R}^n$. It is PL homeomorphic to
$\mathbb {R}^n$. It is PL homeomorphic to ![]() $S^{n-2}\star [0,1]$, the join of
$S^{n-2}\star [0,1]$, the join of ![]() $S^{n-2}$ with
$S^{n-2}$ with ![]() $[0,1]$. Note that for PL manifolds
$[0,1]$. Note that for PL manifolds ![]() $M$ and
$M$ and ![]() $N$, a PL homeomorphism of
$N$, a PL homeomorphism of ![]() $N$ extends naturally to a PL homeomorphism of the join
$N$ extends naturally to a PL homeomorphism of the join ![]() $M\star N$. A glide homeomorphism of the ball
$M\star N$. A glide homeomorphism of the ball ![]() $B$ is a PL homeomorphism that is induced by the extension of a compactly supported PL homeomorphism of
$B$ is a PL homeomorphism that is induced by the extension of a compactly supported PL homeomorphism of ![]() $(0,1)$ to a PL homeomorphism of
$(0,1)$ to a PL homeomorphism of ![]() $S^{n-2}\star [0,1]$. For a PL
$S^{n-2}\star [0,1]$. For a PL ![]() $n$-manifold
$n$-manifold ![]() $M$, a glide homeomorphism
$M$, a glide homeomorphism ![]() $h\colon M\to M$ is the extension by the identity of a glide homeomorphism supported in a PL embedded ball
$h\colon M\to M$ is the extension by the identity of a glide homeomorphism supported in a PL embedded ball ![]() $B\hookrightarrow M$.
$B\hookrightarrow M$.
Question (Epstein)
Is ![]() ${{\mathrm {PL}}}^{\delta }_{0}(M, \mathrm {rel}\,\partial )$ generated by glide homeomorphisms?
${{\mathrm {PL}}}^{\delta }_{0}(M, \mathrm {rel}\,\partial )$ generated by glide homeomorphisms?
The affirmative answer to this question implies that ![]() ${\mathrm {PL}}^{\delta }_{0}(M, \mathrm {rel}\,\partial )$ is simple, and conversely, since the group generated by glide homeomorphisms is a normal subgroup of
${\mathrm {PL}}^{\delta }_{0}(M, \mathrm {rel}\,\partial )$ is simple, and conversely, since the group generated by glide homeomorphisms is a normal subgroup of ![]() ${\mathrm {PL}}^{\delta }_{0}(M, \mathrm {rel}\,\partial )$, if the group
${\mathrm {PL}}^{\delta }_{0}(M, \mathrm {rel}\,\partial )$, if the group ![]() ${\mathrm {PL}}^{\delta }_{0}(M, \mathrm {rel}\,\partial )$ is simple, it is generated by glide homeomorphisms.
${\mathrm {PL}}^{\delta }_{0}(M, \mathrm {rel}\,\partial )$ is simple, it is generated by glide homeomorphisms.
Theorem 1.4 Let ![]() $\Sigma$ be an oriented compact surface possibly with a boundary. Then the group
$\Sigma$ be an oriented compact surface possibly with a boundary. Then the group ![]() ${\mathrm {PL}}^{\delta }_0(\Sigma,\mathrm {rel}\,\partial )$ is simple.
${\mathrm {PL}}^{\delta }_0(\Sigma,\mathrm {rel}\,\partial )$ is simple.
The simplicity of ![]() ${\mathrm {PL}}^{\delta }_{0}(M, \mathrm {rel}\,\partial )$ in all dimensions is still open. We use Theorem 1.2 and the version of the Mather–Thurston theorem that the author proved in [Reference NarimanNar23, § 5] for PL homeomorphisms to prove the perfectness of this group in dimension
${\mathrm {PL}}^{\delta }_{0}(M, \mathrm {rel}\,\partial )$ in all dimensions is still open. We use Theorem 1.2 and the version of the Mather–Thurston theorem that the author proved in [Reference NarimanNar23, § 5] for PL homeomorphisms to prove the perfectness of this group in dimension ![]() $2$, and as a consequence, we answer affirmatively Epstein's question in dimension
$2$, and as a consequence, we answer affirmatively Epstein's question in dimension ![]() $2$.
$2$.
Note that this line of argument is the opposite of Thurston's point of view in the smooth category where he first proved the perfectness of the identity component of smooth diffeomorphism groups to improve the connectivity of the space ![]() $\overline {\mathrm {B}\Gamma }^{\infty }_n$. Our argument gives a homotopy-theoretic proof of the perfectness of
$\overline {\mathrm {B}\Gamma }^{\infty }_n$. Our argument gives a homotopy-theoretic proof of the perfectness of ![]() ${\mathrm {PL}}^{\delta }_{0}(M, \mathrm {rel}\,\partial )$ for a compact surface
${\mathrm {PL}}^{\delta }_{0}(M, \mathrm {rel}\,\partial )$ for a compact surface ![]() $M$. It would be still interesting to find a direct algebraic proof and study the commutator length of PL surface homeomorphisms.
$M$. It would be still interesting to find a direct algebraic proof and study the commutator length of PL surface homeomorphisms.
Recall that the perfectness of a group is equivalent to the vanishing of its first group homology. We in fact determine the group homology of PL surface homeomorphisms up to degree ![]() $2$. By Hauptvermutung in dimension
$2$. By Hauptvermutung in dimension ![]() $2$, any two PL structures on a surface
$2$, any two PL structures on a surface ![]() $\Sigma$ are PL homeomorphic [Reference MoiseMoi77, Chapter 8]. Hence, the homotopy type of
$\Sigma$ are PL homeomorphic [Reference MoiseMoi77, Chapter 8]. Hence, the homotopy type of ![]() $\mathrm {PL}(\Sigma,\mathrm {rel}\,\partial )$ does not depend on the choice of the PL structure on the surface
$\mathrm {PL}(\Sigma,\mathrm {rel}\,\partial )$ does not depend on the choice of the PL structure on the surface ![]() $\Sigma$. Moreover, we have the weak equivalence
$\Sigma$. Moreover, we have the weak equivalence ![]() $\mathrm {PL}(\Sigma,\mathrm {rel}\,\partial )\simeq \mathrm {Homeo}(\Sigma,\mathrm {rel}\,\partial )$ [Reference Balcerak and HajdukBH81, p. 8].
$\mathrm {PL}(\Sigma,\mathrm {rel}\,\partial )\simeq \mathrm {Homeo}(\Sigma,\mathrm {rel}\,\partial )$ [Reference Balcerak and HajdukBH81, p. 8].
Theorem 1.5 Let ![]() $\Sigma$ be a compact orientable surface. Then the natural map
$\Sigma$ be a compact orientable surface. Then the natural map
induces an isomorphism on ![]() $H_*(-;\mathbb {Z})$ for
$H_*(-;\mathbb {Z})$ for ![]() $*\leq 2$ and surjection on
$*\leq 2$ and surjection on ![]() $*=3$.
$*=3$.
Since ![]() $\mathrm {B}{\mathrm {PL}}_0(\Sigma,\mathrm {rel}\,\partial )$ is simply connected, this theorem implies that
$\mathrm {B}{\mathrm {PL}}_0(\Sigma,\mathrm {rel}\,\partial )$ is simply connected, this theorem implies that ![]() ${\mathrm {PL}}^{\delta }_0(\Sigma,\mathrm {rel}\,\partial )$ is a perfect group. Therefore, Theorem 1.5 proves the perfectness of PL homeomorphisms of surfaces without following Epstein's strategy through glide homeomorphisms. On the other hand, by Epstein [Reference EpsteinEps70, Theorem 3.1], the perfectness for the group
${\mathrm {PL}}^{\delta }_0(\Sigma,\mathrm {rel}\,\partial )$ is a perfect group. Therefore, Theorem 1.5 proves the perfectness of PL homeomorphisms of surfaces without following Epstein's strategy through glide homeomorphisms. On the other hand, by Epstein [Reference EpsteinEps70, Theorem 3.1], the perfectness for the group ![]() ${\mathrm {PL}}^{\delta }_0(\Sigma,\mathrm {rel}\,\partial )$ implies that it is also simple. Given that the group generated by glides is a normal subgroup, we can also answer Epstein's question about glide homeomorphisms.
${\mathrm {PL}}^{\delta }_0(\Sigma,\mathrm {rel}\,\partial )$ implies that it is also simple. Given that the group generated by glides is a normal subgroup, we can also answer Epstein's question about glide homeomorphisms.
In fact, the homotopy type of the topological group ![]() ${\mathrm {PL}}_0(\Sigma,\mathrm {rel}\,\partial )$ is completely determined, so the second group homology of
${\mathrm {PL}}_0(\Sigma,\mathrm {rel}\,\partial )$ is completely determined, so the second group homology of ![]() ${\mathrm {PL}}^{\delta }_0(\Sigma,\mathrm {rel}\,\partial )$ can also be determined.
${\mathrm {PL}}^{\delta }_0(\Sigma,\mathrm {rel}\,\partial )$ can also be determined.
Our second application is about the invariants of flat surface bundles with transverse PL structures. We first show that the powers of the universal Euler class are all nontrivial in ![]() $H^{*}(\mathrm {B}\Gamma _2^{\mathrm {PL}};\mathbb {Z})$ and we use it to prove the following result.
$H^{*}(\mathrm {B}\Gamma _2^{\mathrm {PL}};\mathbb {Z})$ and we use it to prove the following result.
Theorem 1.6 Let ![]() $\Sigma$ be a compact orientable surface. Then the map
$\Sigma$ be a compact orientable surface. Then the map
induces an injection when ![]() $*\leq (2g(\Sigma )-2)/3$ where
$*\leq (2g(\Sigma )-2)/3$ where ![]() $g(\Sigma )$ is the genus of the surface
$g(\Sigma )$ is the genus of the surface ![]() $\Sigma$.
$\Sigma$.
As a consequence of the Madsen–Weiss theorem [Reference Madsen and WeissMW07], ![]() $H^*(\mathrm {B}{\mathrm {PL}}(\Sigma,\mathrm {rel}\,\partial );\mathbb {Q})$ is isomorphic to the polynomial ring
$H^*(\mathrm {B}{\mathrm {PL}}(\Sigma,\mathrm {rel}\,\partial );\mathbb {Q})$ is isomorphic to the polynomial ring ![]() $\mathbb {Q}[\kappa _1,\kappa _2,\dots ]$ in the stable range,
$\mathbb {Q}[\kappa _1,\kappa _2,\dots ]$ in the stable range, ![]() $*\leq (2g(\Sigma )-2)/3$. Here
$*\leq (2g(\Sigma )-2)/3$. Here ![]() $\kappa _i$ are certain characteristic classes of surface bundles known as
$\kappa _i$ are certain characteristic classes of surface bundles known as ![]() $i$th Miller–Morita–Mumford (MMM) classes whose degree is
$i$th Miller–Morita–Mumford (MMM) classes whose degree is ![]() $2i$.
$2i$.
Corollary 1.7 The ![]() $\kappa _i$ are all nontrivial in
$\kappa _i$ are all nontrivial in ![]() $H^*(\mathrm {B}{\mathrm {PL}}^{\delta }(\Sigma,\mathrm {rel}\,\partial );\mathbb {Q})$ as long as
$H^*(\mathrm {B}{\mathrm {PL}}^{\delta }(\Sigma,\mathrm {rel}\,\partial );\mathbb {Q})$ as long as ![]() $i\leq (2g(\Sigma )-2)/6$.
$i\leq (2g(\Sigma )-2)/6$.
This is in contrast to the case of smooth diffeomorphisms. It is known by the Bott vanishing theorem [Reference MoritaMor87, Theorem 8.1] that ![]() $\kappa _i$ vanishes in
$\kappa _i$ vanishes in ![]() $H^*(\mathrm {BDiff}^{\delta }(\Sigma,\mathrm {rel}\,\partial );\mathbb {Q})$ for all
$H^*(\mathrm {BDiff}^{\delta }(\Sigma,\mathrm {rel}\,\partial );\mathbb {Q})$ for all ![]() $i>2$, and Kotschick and Morita [Reference Kotschick and MoritaKM05] proved that
$i>2$, and Kotschick and Morita [Reference Kotschick and MoritaKM05] proved that ![]() $\kappa _1$ is nontrivial in
$\kappa _1$ is nontrivial in ![]() $H^2(\mathrm {BDiff}^{\delta }(\Sigma,\mathrm {rel}\,\partial );\mathbb {Q})$ as long as
$H^2(\mathrm {BDiff}^{\delta }(\Sigma,\mathrm {rel}\,\partial );\mathbb {Q})$ as long as ![]() $g(\Sigma )\geq 3$. However, it is still open [Reference Kotschick and MoritaKM05] whether
$g(\Sigma )\geq 3$. However, it is still open [Reference Kotschick and MoritaKM05] whether ![]() $\kappa _2$ is nontrivial in
$\kappa _2$ is nontrivial in ![]() $H^4(\mathrm {BDiff}^{\delta }(\Sigma, \mathrm {rel}\,\partial );\mathbb {Q})$.
$H^4(\mathrm {BDiff}^{\delta }(\Sigma, \mathrm {rel}\,\partial );\mathbb {Q})$.
2. The curious case of PL foliations
In this section, we are mainly concerned with codimension ![]() $2$ PL foliations that are co-oriented (i.e., their normal bundles are oriented). The Haefliger classifying space for these structures
$2$ PL foliations that are co-oriented (i.e., their normal bundles are oriented). The Haefliger classifying space for these structures ![]() $\mathrm {B}\Gamma _2^{\mathrm {PL}}$ is the (fat) geometric realization of the nerve of the étale groupoid
$\mathrm {B}\Gamma _2^{\mathrm {PL}}$ is the (fat) geometric realization of the nerve of the étale groupoid ![]() $\Gamma _2^{\mathrm {PL}}$ whose space of objects is
$\Gamma _2^{\mathrm {PL}}$ whose space of objects is ![]() $\mathbb {R}^2$ with the usual topology and the space of morphisms are germs of orientation-preserving PL homeomorphisms of
$\mathbb {R}^2$ with the usual topology and the space of morphisms are germs of orientation-preserving PL homeomorphisms of ![]() $\mathbb {R}^2$ with the sheaf topology [Reference MatherMat11, § 1]. The main inputs to prove Theorem 1.2 are Greenberg's inductive model for the classifying space PL foliations [Reference GreenbergGre92] and Suslin's work [Reference SuslinSus91] on low-degree K-groups of real numbers. And then we use our variant of the Mather–Thurston theorem [Reference NarimanNar23] for PL homeomorphisms to relate the connectivity of
$\mathbb {R}^2$ with the sheaf topology [Reference MatherMat11, § 1]. The main inputs to prove Theorem 1.2 are Greenberg's inductive model for the classifying space PL foliations [Reference GreenbergGre92] and Suslin's work [Reference SuslinSus91] on low-degree K-groups of real numbers. And then we use our variant of the Mather–Thurston theorem [Reference NarimanNar23] for PL homeomorphisms to relate the connectivity of ![]() $\overline {\mathrm {B}\Gamma }_2^{\mathrm {PL}}$ to the homology of PL surface homeomorphisms.
$\overline {\mathrm {B}\Gamma }_2^{\mathrm {PL}}$ to the homology of PL surface homeomorphisms.
We first recall Greenberg's recursive construction for such classifying spaces [Reference GreenbergGre92, Theorem 3.2(c)] in the case that we are interested in.
2.1 Greenberg's construction and the connectivity of  $\overline {\mathrm {B}\Gamma }_2^{\mathrm {PL}}$
$\overline {\mathrm {B}\Gamma }_2^{\mathrm {PL}}$
Let ![]() $A$ be the subgroup of
$A$ be the subgroup of ![]() $\mathrm {GL}_2^+(\mathbb {R})$ consisting of matrices of the form
$\mathrm {GL}_2^+(\mathbb {R})$ consisting of matrices of the form
where ![]() $a$ and
$a$ and ![]() $d$ are positive reals. Let
$d$ are positive reals. Let ![]() $\epsilon \colon A\to \mathbb {R}^+$ be the homomorphism
$\epsilon \colon A\to \mathbb {R}^+$ be the homomorphism ![]() $\epsilon (M)=a$. Let
$\epsilon (M)=a$. Let ![]() $R_A$ be the following homotopy pushout:
$R_A$ be the following homotopy pushout:
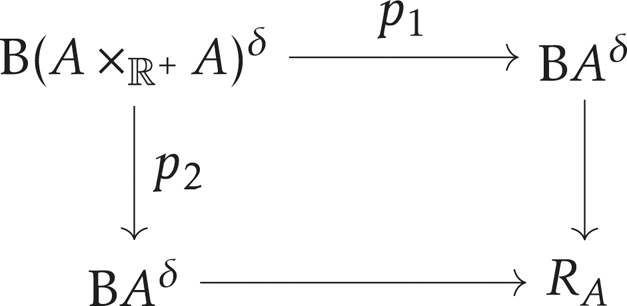
where the ![]() $p_i$ are induced by the projection to the
$p_i$ are induced by the projection to the ![]() $i$th factor and
$i$th factor and ![]() $A\times _{\mathbb {R}^+} A$ is the fiber products of
$A\times _{\mathbb {R}^+} A$ is the fiber products of ![]() $A$ over
$A$ over ![]() $\mathbb {R}^+$ using the map
$\mathbb {R}^+$ using the map ![]() $\epsilon$. Let
$\epsilon$. Let ![]() $\widetilde {\mathrm {GL}_2^+}(\mathbb {R})$ be the universal cover of
$\widetilde {\mathrm {GL}_2^+}(\mathbb {R})$ be the universal cover of ![]() $\mathrm {GL}_2^+(\mathbb {R})$. Note that the inclusion of
$\mathrm {GL}_2^+(\mathbb {R})$. Note that the inclusion of ![]() $A$ into
$A$ into ![]() $\mathrm {GL}_2^+(\mathbb {R})$ lifts to the universal cover
$\mathrm {GL}_2^+(\mathbb {R})$ lifts to the universal cover ![]() $\widetilde {\mathrm {GL}_2^+}(\mathbb {R})$. Let the map
$\widetilde {\mathrm {GL}_2^+}(\mathbb {R})$. Let the map ![]() $\alpha \colon \mathrm {B}A^{\delta }\to R_A$ be induced by the diagonal embedding
$\alpha \colon \mathrm {B}A^{\delta }\to R_A$ be induced by the diagonal embedding ![]() $A\to A\times _{\mathbb {R}^+} A$ and then composing with
$A\to A\times _{\mathbb {R}^+} A$ and then composing with ![]() $\mathrm {B}(A\times _{\mathbb {R}^+} A)^{\delta }\to R_A$. We let
$\mathrm {B}(A\times _{\mathbb {R}^+} A)^{\delta }\to R_A$. We let ![]() $X$ be the homotopy pushout of the following diagram:
$X$ be the homotopy pushout of the following diagram:
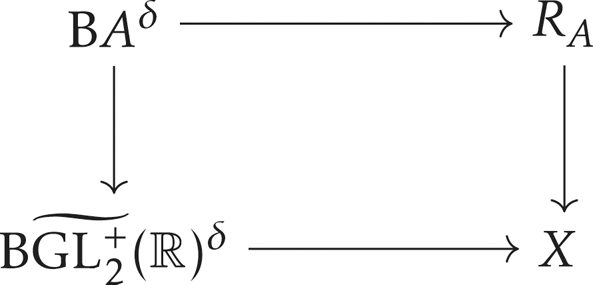
Finally, let ![]() $LX$ be the space of continuous free loops in
$LX$ be the space of continuous free loops in ![]() $X$ and let
$X$ and let ![]() $LX/\!\!/ S^1$ be the homotopy quotient of the circle action on
$LX/\!\!/ S^1$ be the homotopy quotient of the circle action on ![]() $LX$. We define
$LX$. We define ![]() $rX$ to be the homotopy pushout
$rX$ to be the homotopy pushout
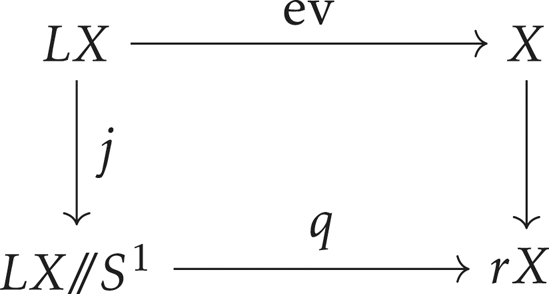
where ![]() $\mathrm {ev}\colon LX\to X$ is the evaluation of the loops at their base point and
$\mathrm {ev}\colon LX\to X$ is the evaluation of the loops at their base point and ![]() $j$ is the inclusion of the fiber in the Borel fibration
$j$ is the inclusion of the fiber in the Borel fibration ![]() $LX\to LX/\!\!/ S^1\to \mathrm {B}S^1$. Greenberg's theorem [Reference GreenbergGre92, Theorem 3.2(c)] says that
$LX\to LX/\!\!/ S^1\to \mathrm {B}S^1$. Greenberg's theorem [Reference GreenbergGre92, Theorem 3.2(c)] says that ![]() $rX\simeq \mathrm {B}\Gamma _2^{\mathrm {PL}}$.Footnote 1 Recall that
$rX\simeq \mathrm {B}\Gamma _2^{\mathrm {PL}}$.Footnote 1 Recall that ![]() $\overline {\mathrm {B}\Gamma }_2^{\mathrm {PL}}$ is the homotopy fiber of the map
$\overline {\mathrm {B}\Gamma }_2^{\mathrm {PL}}$ is the homotopy fiber of the map
and it was already known as we mentioned in the introduction that ![]() $\overline {\mathrm {B}\Gamma }_2^{\mathrm {PL}}$ is at least
$\overline {\mathrm {B}\Gamma }_2^{\mathrm {PL}}$ is at least ![]() $2$-connected. So to prove Theorem 1.2, it is enough to show that the map
$2$-connected. So to prove Theorem 1.2, it is enough to show that the map ![]() $\nu$ induces a homology isomorphism up to and including degree
$\nu$ induces a homology isomorphism up to and including degree ![]() $4$. To do this, we shall calculate the homology of
$4$. To do this, we shall calculate the homology of ![]() $rX$ using the Mayer–Vietoris sequence for the homotopy pushout square (
$rX$ using the Mayer–Vietoris sequence for the homotopy pushout square (
). But we first need to prove the following key lemma about the homotopy type of ![]() $X$.
$X$.
Theorem 2.4 The space ![]() $X$ is
$X$ is ![]() $2$-connected.
$2$-connected.
The fact that ![]() $X$ is simply connected was already observed by Greenberg [Reference GreenbergGre92, Proof of Corollary 2.6]. This can also be seen using Van Kampen's theorem to compute the fundamental group. The map
$X$ is simply connected was already observed by Greenberg [Reference GreenbergGre92, Proof of Corollary 2.6]. This can also be seen using Van Kampen's theorem to compute the fundamental group. The map ![]() $\mathrm {B}\epsilon \colon \mathrm {B}A^{\delta }\to \mathrm {B}\mathbb {R}^{+,\delta }$ induces a map
$\mathrm {B}\epsilon \colon \mathrm {B}A^{\delta }\to \mathrm {B}\mathbb {R}^{+,\delta }$ induces a map ![]() $h\colon R_A\to \mathrm {B}\mathbb {R}^{+,\delta }$. Using Van Kampen's theorem, one can easily see that
$h\colon R_A\to \mathrm {B}\mathbb {R}^{+,\delta }$. Using Van Kampen's theorem, one can easily see that ![]() $h$ induces an isomorphism
$h$ induces an isomorphism ![]() $\pi _1(R_A)\xrightarrow {\cong } \mathbb {R}^+$. So
$\pi _1(R_A)\xrightarrow {\cong } \mathbb {R}^+$. So ![]() $\pi _1(X)$ is isomorphic to the quotient of
$\pi _1(X)$ is isomorphic to the quotient of ![]() $\widetilde {\mathrm {GL}_2^+}(\mathbb {R})^{\delta }$ by the smallest normal subgroup generated by the image of
$\widetilde {\mathrm {GL}_2^+}(\mathbb {R})^{\delta }$ by the smallest normal subgroup generated by the image of ![]() $\mathrm {ker}(\epsilon )$. A priori,
$\mathrm {ker}(\epsilon )$. A priori, ![]() $\mathrm {ker}(\epsilon )$ lies in
$\mathrm {ker}(\epsilon )$ lies in ![]() $\mathrm {GL}_2^+(\mathbb {R})^{\delta }$ and it is easy to see that it normally generates the entire group
$\mathrm {GL}_2^+(\mathbb {R})^{\delta }$ and it is easy to see that it normally generates the entire group ![]() $\mathrm {GL}_2^+(\mathbb {R})^{\delta }$. Therefore, its lift also normally generates
$\mathrm {GL}_2^+(\mathbb {R})^{\delta }$. Therefore, its lift also normally generates ![]() $\widetilde {\mathrm {GL}_2^+}(\mathbb {R})^{\delta }$. Hence,
$\widetilde {\mathrm {GL}_2^+}(\mathbb {R})^{\delta }$. Hence, ![]() $\pi _1(X)$ is trivial.
$\pi _1(X)$ is trivial.
One can use the Milnor–Friedlander conjecture for solvable Lie groups which was already proved in Milnor's original paper [Reference MilnorMil83] on this topic and Suslin's stability theorem [Reference SuslinSus84] to show that ![]() $\pi _2(X)\otimes \mathbb {F}_p=0$ for all prime
$\pi _2(X)\otimes \mathbb {F}_p=0$ for all prime ![]() $p$. But to prove the integral result that
$p$. But to prove the integral result that ![]() $\pi _2(X)=0$ we need to work a bit harder.
$\pi _2(X)=0$ we need to work a bit harder.
Remark 2.2 To see that ![]() $\pi _2(X)\otimes \mathbb {F}_p=0$, by the Hurewicz theorem, it is enough to show that the group
$\pi _2(X)\otimes \mathbb {F}_p=0$, by the Hurewicz theorem, it is enough to show that the group ![]() $H_2(X;\mathbb {F}_p)$ vanishes for all prime
$H_2(X;\mathbb {F}_p)$ vanishes for all prime ![]() $p$. We shall first observe that
$p$. We shall first observe that ![]() $R_A$ is an
$R_A$ is an ![]() $\mathbb {F}_p$-acyclic space, that is,
$\mathbb {F}_p$-acyclic space, that is, ![]() $H_*(R_A;\mathbb {F}_p)=0$ for all
$H_*(R_A;\mathbb {F}_p)=0$ for all ![]() $*>0$. We have the short exact sequence of groups
$*>0$. We have the short exact sequence of groups
Therefore, the group ![]() $A^{\delta }$ is solvable. Similarly,
$A^{\delta }$ is solvable. Similarly, ![]() $(A\times _{\mathbb {R}^+} A)^{\delta }$ is solvable. On the other hand, as topological groups, both
$(A\times _{\mathbb {R}^+} A)^{\delta }$ is solvable. On the other hand, as topological groups, both ![]() $A$ and
$A$ and ![]() $A\times _{\mathbb {R}^+} A$ are contractible. Hence, by Milnor's theorem [Reference MilnorMil83, Lemma 3], the groups
$A\times _{\mathbb {R}^+} A$ are contractible. Hence, by Milnor's theorem [Reference MilnorMil83, Lemma 3], the groups ![]() $A$ and
$A$ and ![]() $A\times _{\mathbb {R}^+} A$ are
$A\times _{\mathbb {R}^+} A$ are ![]() $\mathbb {F}_p$-acyclic for all prime
$\mathbb {F}_p$-acyclic for all prime ![]() $p$, and by applying the Mayer–Vietoris sequence to the pushout (2.1) we deduce that
$p$, and by applying the Mayer–Vietoris sequence to the pushout (2.1) we deduce that ![]() $R_A$ is also
$R_A$ is also ![]() $\mathbb {F}_p$-acyclic for all prime
$\mathbb {F}_p$-acyclic for all prime ![]() $p$. Now using the Mayer–Vietoris sequence with
$p$. Now using the Mayer–Vietoris sequence with ![]() $\mathbb {F}_p$ coefficients for the pushout (2.2), it is enough to show that
$\mathbb {F}_p$ coefficients for the pushout (2.2), it is enough to show that ![]() $H_2(\mathrm {B}\widetilde {\mathrm {GL}_2^+}(\mathbb {R})^{\delta };\mathbb {F}_p)=0$. Recall that we know by Suslin's theorem [Reference SuslinSus84] that in general the map
$H_2(\mathrm {B}\widetilde {\mathrm {GL}_2^+}(\mathbb {R})^{\delta };\mathbb {F}_p)=0$. Recall that we know by Suslin's theorem [Reference SuslinSus84] that in general the map
induces an isomorphism on ![]() $H_*(-;\mathbb {F}_p)$ for
$H_*(-;\mathbb {F}_p)$ for ![]() $*\leq n$. On the other hand, we have a short exact sequence
$*\leq n$. On the other hand, we have a short exact sequence
Therefore, by a spectral sequence argument, we deduce that the map
induces an isomorphism on ![]() $H_*(-;\mathbb {F}_p)$ for
$H_*(-;\mathbb {F}_p)$ for ![]() $*\leq 2$. But
$*\leq 2$. But ![]() $\widetilde {\mathrm {GL}_2^+}(\mathbb {R})$ is contractible which implies that
$\widetilde {\mathrm {GL}_2^+}(\mathbb {R})$ is contractible which implies that ![]() $H_2(\mathrm {B}\widetilde {\mathrm {GL}_2^+}(\mathbb {R})^{\delta };\mathbb {F}_p)=0$.
$H_2(\mathrm {B}\widetilde {\mathrm {GL}_2^+}(\mathbb {R})^{\delta };\mathbb {F}_p)=0$.
To prove Theorem 2.4, we need some preliminary lemmas to do the calculations integrally.
Lemma 2.6 Let ![]() $D$ be the subgroup of diagonal matrices in
$D$ be the subgroup of diagonal matrices in ![]() $A$. Let
$A$. Let ![]() $\iota \colon D\hookrightarrow A$ be the inclusion map of the subgroup of diagonal matrices. The map
$\iota \colon D\hookrightarrow A$ be the inclusion map of the subgroup of diagonal matrices. The map ![]() $\iota$ has a left inverse
$\iota$ has a left inverse ![]() $r\colon A\to D$,
$r\colon A\to D$,
The maps ![]() $\tilde {\iota }$ and
$\tilde {\iota }$ and ![]() $\tilde {r}$,
$\tilde {r}$,
induce homology isomorphisms.
Proof. There is a trick that apparently goes back to Quillen over rational coefficients [Reference de La Harpe and McDuffdLHM83, Lemma 4] and to Nesterenko and Suslin [Reference Nesterenko and SuslinNS90, Theorem 1.11] over integer coefficients that the map ![]() $\mathrm {B}\mathrm {GL}_n^+(\mathbb {R})^\delta \to \mathrm {B}\mathrm {Aff}^+(\mathbb {R}^n)^{\delta }$, which also has a left inverse, induces a homology isomorphism. Taking
$\mathrm {B}\mathrm {GL}_n^+(\mathbb {R})^\delta \to \mathrm {B}\mathrm {Aff}^+(\mathbb {R}^n)^{\delta }$, which also has a left inverse, induces a homology isomorphism. Taking ![]() $n=1$, we have a map between fibrations
$n=1$, we have a map between fibrations
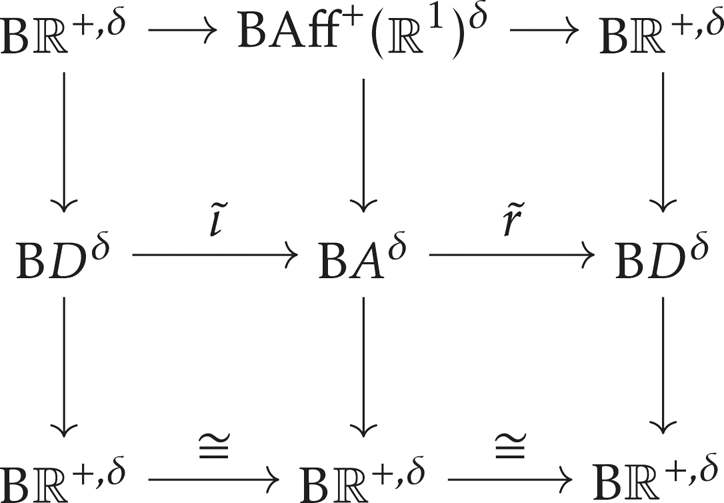
where the top horizontal maps induce homology isomorphisms and the bottom maps are the identity. Therefore, by the comparison of Serre spectral sequences, ![]() $\tilde {\iota }$ and
$\tilde {\iota }$ and ![]() $\tilde {r}$ also induce homology isomorphisms.
$\tilde {r}$ also induce homology isomorphisms.
Let ![]() $Y$ be the homotopy pushout of the diagram
$Y$ be the homotopy pushout of the diagram
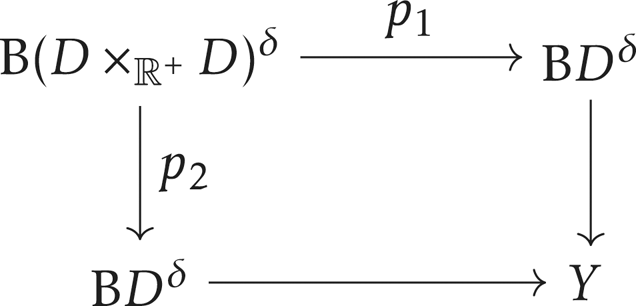
Given that we have the inclusion ![]() $D\xrightarrow {\iota } A$ and its left inverse
$D\xrightarrow {\iota } A$ and its left inverse ![]() $r$, we have a natural map
$r$, we have a natural map ![]() $\theta \colon Y\to R_A$.
$\theta \colon Y\to R_A$.
Lemma 2.9 The map ![]() $\theta \colon Y\to R_A$ admits a left inverse and it induces a homology isomorphism. The space
$\theta \colon Y\to R_A$ admits a left inverse and it induces a homology isomorphism. The space ![]() $Y$ is homotopy equivalent to
$Y$ is homotopy equivalent to ![]() $\mathrm {B} \mathbb {R}^{+,\delta } \times (\mathrm {B} \mathbb {R}^{+,\delta }\star \mathrm {B} \mathbb {R}^{+,\delta })\to R_A$ where
$\mathrm {B} \mathbb {R}^{+,\delta } \times (\mathrm {B} \mathbb {R}^{+,\delta }\star \mathrm {B} \mathbb {R}^{+,\delta })\to R_A$ where ![]() $\star$ means the join of topological spaces.
$\star$ means the join of topological spaces.
Proof. The inclusion ![]() $D\xrightarrow {\iota } A$ induces a map of homotopy pushout diagrams from (2.8) to (2.1) and the left inverse
$D\xrightarrow {\iota } A$ induces a map of homotopy pushout diagrams from (2.8) to (2.1) and the left inverse ![]() $r$ induces a map of diagrams from (2.1) to (2.8) which gives the left inverse to
$r$ induces a map of diagrams from (2.1) to (2.8) which gives the left inverse to ![]() $\theta$. Since the maps between corresponding terms induce homology isomorphisms by Lemma 2.6, the Mayer–Vietoris sequence implies that
$\theta$. Since the maps between corresponding terms induce homology isomorphisms by Lemma 2.6, the Mayer–Vietoris sequence implies that ![]() $\theta$ induces a homology isomorphism.
$\theta$ induces a homology isomorphism.
To see that ![]() $Y$ is homotopy equivalent to
$Y$ is homotopy equivalent to ![]() $\mathrm {B} \mathbb {R}^{+,\delta } \times (\mathrm {B} \mathbb {R}^{+,\delta }\star \mathrm {B} \mathbb {R}^{+,\delta })$, note that
$\mathrm {B} \mathbb {R}^{+,\delta } \times (\mathrm {B} \mathbb {R}^{+,\delta }\star \mathrm {B} \mathbb {R}^{+,\delta })$, note that ![]() $D$ is isomorphic to
$D$ is isomorphic to ![]() $\mathbb {R}^{+}\times \mathbb {R}^{+}$. So
$\mathbb {R}^{+}\times \mathbb {R}^{+}$. So ![]() $Y$ is homotopy equivalent to the homotopy pushout of
$Y$ is homotopy equivalent to the homotopy pushout of
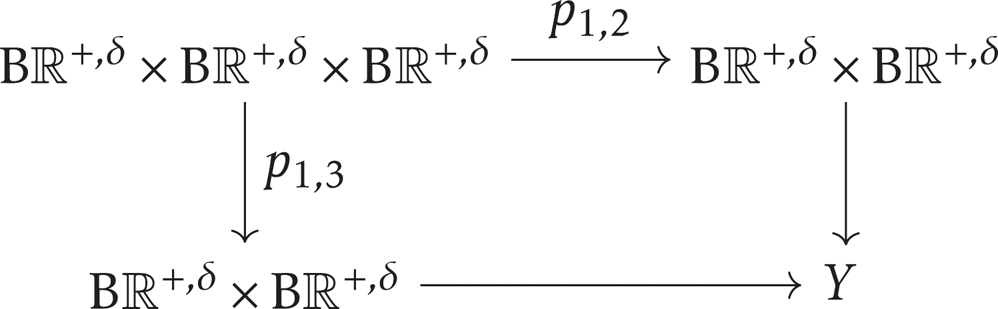
where ![]() $p_{1,i}$ is the projection to the first and the
$p_{1,i}$ is the projection to the first and the ![]() $i$th factor. Therefore,
$i$th factor. Therefore, ![]() $Y$ is homotopy equivalent to
$Y$ is homotopy equivalent to ![]() $\mathrm {B} \mathbb {R}^{+,\delta } \times (\mathrm {B} \mathbb {R}^{+,\delta }\star \mathrm {B} \mathbb {R}^{+,\delta })$.
$\mathrm {B} \mathbb {R}^{+,\delta } \times (\mathrm {B} \mathbb {R}^{+,\delta }\star \mathrm {B} \mathbb {R}^{+,\delta })$.
Recall that the map ![]() $\alpha \colon \mathrm {B}A^{\delta }\to R_A$ is defined to be the composition of the diagonal embedding
$\alpha \colon \mathrm {B}A^{\delta }\to R_A$ is defined to be the composition of the diagonal embedding ![]() $\mathrm {B}A^{\delta }\to \mathrm {B}(A\times _{\mathbb {R}^+} A)^{\delta }$ and
$\mathrm {B}A^{\delta }\to \mathrm {B}(A\times _{\mathbb {R}^+} A)^{\delta }$ and ![]() $\mathrm {B}(A\times _{\mathbb {R}^+} A)^{\delta }\to R_A$. Similarly, we obtain a map
$\mathrm {B}(A\times _{\mathbb {R}^+} A)^{\delta }\to R_A$. Similarly, we obtain a map ![]() $\beta \colon \mathrm {B}D^{\delta }\to Y$. So we have a commutative diagram
$\beta \colon \mathrm {B}D^{\delta }\to Y$. So we have a commutative diagram
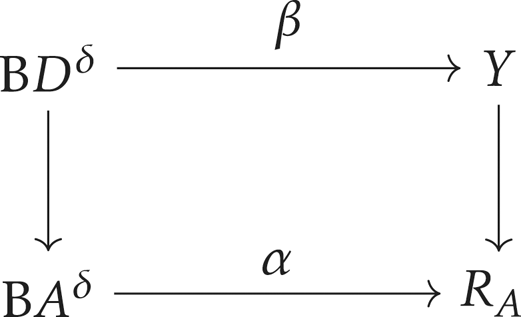
where the vertical maps induce homology isomorphisms. Note that the join ![]() $\mathrm {B} \mathbb {R}^{+,\delta }\star \mathrm {B} \mathbb {R}^{+,\delta }$ is
$\mathrm {B} \mathbb {R}^{+,\delta }\star \mathrm {B} \mathbb {R}^{+,\delta }$ is ![]() $2$-connected and there is an isomorphism from
$2$-connected and there is an isomorphism from ![]() $H_*(\mathrm {B} \mathbb {R}^{+,\delta }; \mathbb {Z})$ to
$H_*(\mathrm {B} \mathbb {R}^{+,\delta }; \mathbb {Z})$ to ![]() $\bigwedge ^*\mathbb {R}^+$ which is an exterior product of
$\bigwedge ^*\mathbb {R}^+$ which is an exterior product of ![]() $\mathbb {R}^+$ over
$\mathbb {R}^+$ over ![]() $\mathbb {Z}$. By considering the commutative diagram
$\mathbb {Z}$. By considering the commutative diagram
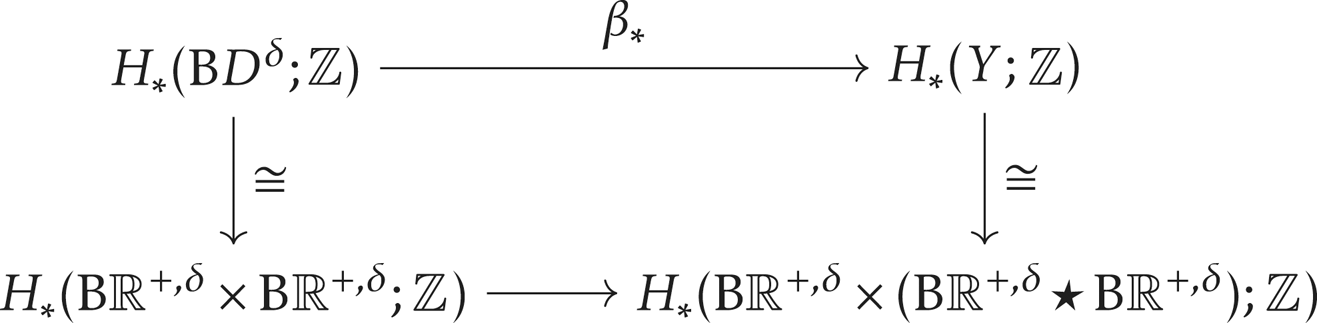
and using Künneth's formula, it is easy to determine the kernel of the map ![]() $\beta _*$ in low homological degrees. So we record the following corollary about
$\beta _*$ in low homological degrees. So we record the following corollary about ![]() $\ker \alpha _{*}$ in low homological degrees where
$\ker \alpha _{*}$ in low homological degrees where
Corollary 2.13 Let ![]() $t\colon \mathbb {R}^+\to A$ be the map
$t\colon \mathbb {R}^+\to A$ be the map ![]() $t(a)=\big [\begin{smallmatrix} 1 & 0 \\ 0 & a \end{smallmatrix}\big ]$ and let
$t(a)=\big [\begin{smallmatrix} 1 & 0 \\ 0 & a \end{smallmatrix}\big ]$ and let ![]() $s\colon \mathbb {R}^+\to A$ be the map
$s\colon \mathbb {R}^+\to A$ be the map ![]() $s(a)=\big [\begin{smallmatrix} a & 0 \\ 0 & 1 \end{smallmatrix}\big ]$.
$s(a)=\big [\begin{smallmatrix} a & 0 \\ 0 & 1 \end{smallmatrix}\big ]$.
(1) The map
 $\iota \colon \mathbb {R}^+\times \mathbb {R}^+\cong D\to A$ induces a split surjection
which maps the first summand
$\iota \colon \mathbb {R}^+\times \mathbb {R}^+\cong D\to A$ induces a split surjection
which maps the first summand \[ \bigwedge^2\mathbb{R}^+\oplus (\mathbb{R}^+\otimes \mathbb{R}^+)\oplus \bigwedge^2\mathbb{R}^+\cong H_2(\textrm{B}D^{\delta}; \mathbb{Z})\xrightarrow{\cong} H_2(\textrm{B}A^{\delta}; \mathbb{Z})\to H_2(R_A; \mathbb{Z})\cong \bigwedge^2\mathbb{R}^+, \]
\[ \bigwedge^2\mathbb{R}^+\oplus (\mathbb{R}^+\otimes \mathbb{R}^+)\oplus \bigwedge^2\mathbb{R}^+\cong H_2(\textrm{B}D^{\delta}; \mathbb{Z})\xrightarrow{\cong} H_2(\textrm{B}A^{\delta}; \mathbb{Z})\to H_2(R_A; \mathbb{Z})\cong \bigwedge^2\mathbb{R}^+, \]
 $\bigwedge ^2\mathbb {R}^+$ isomorphically to
$\bigwedge ^2\mathbb {R}^+$ isomorphically to  $H_2(R_A; \mathbb {Z})$. So
$H_2(R_A; \mathbb {Z})$. So  $\ker \alpha _2$ is isomorphic to
$\ker \alpha _2$ is isomorphic to  $(\mathbb {R}^+\otimes \mathbb {R}^+)\oplus \bigwedge ^2\mathbb {R}^+$.
$(\mathbb {R}^+\otimes \mathbb {R}^+)\oplus \bigwedge ^2\mathbb {R}^+$.(2) The map
 $t$ induces an isomorphism
$t$ induces an isomorphism  $\mathbb {R}^+\cong H_1(\mathrm {B} \mathbb {R}^{+,\delta }; \mathbb {Z})\to \ker \alpha _{1}$ and an injective map
$\mathbb {R}^+\cong H_1(\mathrm {B} \mathbb {R}^{+,\delta }; \mathbb {Z})\to \ker \alpha _{1}$ and an injective map  $\bigwedge ^2\mathbb {R}^+\cong H_2(\mathrm {B} \mathbb {R}^{+,\delta }; \mathbb {Z})\to \ker \alpha _{2}$ which is an isomorphism to the
$\bigwedge ^2\mathbb {R}^+\cong H_2(\mathrm {B} \mathbb {R}^{+,\delta }; \mathbb {Z})\to \ker \alpha _{2}$ which is an isomorphism to the  $\bigwedge ^2\mathbb {R}^+$ summand of
$\bigwedge ^2\mathbb {R}^+$ summand of  $\ker \alpha _{2}$ in the identification in item (1) above.
$\ker \alpha _{2}$ in the identification in item (1) above.(3) The composition
where the first map is induced by \[ \bigwedge^2\mathbb{R}^+\cong H_2(\textrm{B}\mathbb{R}^{+,\delta}; \mathbb{Z})\xrightarrow{s_2}H_2(\textrm{B}A^{\delta}; \mathbb{Z})\to H_2(R_A; \mathbb{Z})\cong \bigwedge^2\mathbb{R}^+, \]
\[ \bigwedge^2\mathbb{R}^+\cong H_2(\textrm{B}\mathbb{R}^{+,\delta}; \mathbb{Z})\xrightarrow{s_2}H_2(\textrm{B}A^{\delta}; \mathbb{Z})\to H_2(R_A; \mathbb{Z})\cong \bigwedge^2\mathbb{R}^+, \]
 $s$, is an isomorphism.
$s$, is an isomorphism.
We also need part of Suslin's calculation [Reference SuslinSus91, Theorem 2.1] and [Reference WeibelWei13, Chapter 6, § 5, Proof of Theorem 5.7] of ![]() $H_2(\mathrm {B}\mathrm {GL}_2(\mathbb {R})^{\delta }; \mathbb {Z})$ to determine the image of
$H_2(\mathrm {B}\mathrm {GL}_2(\mathbb {R})^{\delta }; \mathbb {Z})$ to determine the image of
To find ![]() $H_2(\mathrm {B}\widetilde {\mathrm {GL}_2^+}(\mathbb {R})^{\delta }; \mathbb {Z})$, first note that there is an isomorphism
$H_2(\mathrm {B}\widetilde {\mathrm {GL}_2^+}(\mathbb {R})^{\delta }; \mathbb {Z})$, first note that there is an isomorphism ![]() $f\colon \mathrm {SL}_2(\mathbb {R})\times \mathbb {R}^{+}\xrightarrow {\cong } \mathrm {GL}_2^+(\mathbb {R})$ where
$f\colon \mathrm {SL}_2(\mathbb {R})\times \mathbb {R}^{+}\xrightarrow {\cong } \mathrm {GL}_2^+(\mathbb {R})$ where
This isomorphism can be lifted to give an isomorphism ![]() $\tilde {f}\colon \widetilde {\mathrm {SL}_2}(\mathbb {R})\times \mathbb {R}^{+}\xrightarrow {\cong } \widetilde {\mathrm {GL}_2^+}(\mathbb {R})$. On the other hand, the groups
$\tilde {f}\colon \widetilde {\mathrm {SL}_2}(\mathbb {R})\times \mathbb {R}^{+}\xrightarrow {\cong } \widetilde {\mathrm {GL}_2^+}(\mathbb {R})$. On the other hand, the groups ![]() $\mathrm {SL}_2(\mathbb {R})^{\delta }$ and
$\mathrm {SL}_2(\mathbb {R})^{\delta }$ and ![]() $\widetilde {\mathrm {SL}_2}(\mathbb {R})^{\delta }$ are perfect and it is known [Reference Parry and SahPS83, pp. 190–191] that
$\widetilde {\mathrm {SL}_2}(\mathbb {R})^{\delta }$ are perfect and it is known [Reference Parry and SahPS83, pp. 190–191] that ![]() $H_2(\mathrm {B}\widetilde {\mathrm {SL}_2}(\mathbb {R})^{\delta }; \mathbb {Z})\cong K_2(\mathbb {R}),$ and we have a short exact sequence
$H_2(\mathrm {B}\widetilde {\mathrm {SL}_2}(\mathbb {R})^{\delta }; \mathbb {Z})\cong K_2(\mathbb {R}),$ and we have a short exact sequence
Therefore, the Künneth formula implies that we have the isomorphism ![]() $H_2(\mathrm {B}\widetilde {\mathrm {GL}_2^+}(\mathbb {R})^{\delta }; \mathbb {Z})\cong K_2(\mathbb {R})\oplus \bigwedge ^2 \mathbb {R}^{+}$ where
$H_2(\mathrm {B}\widetilde {\mathrm {GL}_2^+}(\mathbb {R})^{\delta }; \mathbb {Z})\cong K_2(\mathbb {R})\oplus \bigwedge ^2 \mathbb {R}^{+}$ where ![]() $K_2(\mathbb {R})$ summand comes from the image of
$K_2(\mathbb {R})$ summand comes from the image of ![]() $H_2(\mathrm {B}\widetilde {\mathrm {SL}_2}(\mathbb {R})^{\delta }; \mathbb {Z})\to H_2(\mathrm {B}\widetilde {\mathrm {GL}_2^+}(\mathbb {R})^{\delta }; \mathbb {Z})$. Also the map
$H_2(\mathrm {B}\widetilde {\mathrm {SL}_2}(\mathbb {R})^{\delta }; \mathbb {Z})\to H_2(\mathrm {B}\widetilde {\mathrm {GL}_2^+}(\mathbb {R})^{\delta }; \mathbb {Z})$. Also the map
is split injective with a co-kernel which is isomorphic to ![]() $\mathbb {Z}$.
$\mathbb {Z}$.
The map ![]() $\mathbb {R}^+\times \mathbb {R}^+\cong D\to A\to \mathrm {GL}_2^+(\mathbb {R})$ induces the map
$\mathbb {R}^+\times \mathbb {R}^+\cong D\to A\to \mathrm {GL}_2^+(\mathbb {R})$ induces the map
Let ![]() $\sigma$ be the involution of diagonal entries of
$\sigma$ be the involution of diagonal entries of ![]() $D\cong \mathbb {R}^+\times \mathbb {R}^+$. The spectral sequence in the proof of [Reference WeibelWei13, Chapter 6, Theorem 5.7] implies that this map factors through the co-invariants
$D\cong \mathbb {R}^+\times \mathbb {R}^+$. The spectral sequence in the proof of [Reference WeibelWei13, Chapter 6, Theorem 5.7] implies that this map factors through the co-invariants
The group ![]() $H_2(\mathrm {B} \mathbb {R}^{+,\delta }\times \mathrm {B} \mathbb {R}^{+,\delta }; \mathbb {Z})_{\sigma }$ is isomorphic to
$H_2(\mathrm {B} \mathbb {R}^{+,\delta }\times \mathrm {B} \mathbb {R}^{+,\delta }; \mathbb {Z})_{\sigma }$ is isomorphic to ![]() $\bigwedge ^2\mathbb {R}^+\oplus \tilde {\bigwedge }^2\mathbb {R}^+$, where
$\bigwedge ^2\mathbb {R}^+\oplus \tilde {\bigwedge }^2\mathbb {R}^+$, where ![]() $\tilde {\bigwedge }^2\mathbb {R}^+$ denotes the quotient of the group
$\tilde {\bigwedge }^2\mathbb {R}^+$ denotes the quotient of the group ![]() $\mathbb {R}^+\otimes \mathbb {R}^+$ by the subgroup generated by all
$\mathbb {R}^+\otimes \mathbb {R}^+$ by the subgroup generated by all ![]() $a\otimes b+b\otimes a$. The proof of [Reference WeibelWei13, Chapter 6, Theorem 5.7] also implies that the restriction of the map
$a\otimes b+b\otimes a$. The proof of [Reference WeibelWei13, Chapter 6, Theorem 5.7] also implies that the restriction of the map
on the summand ![]() $\bigwedge ^2\mathbb {R}^+$ is injective and maps
$\bigwedge ^2\mathbb {R}^+$ is injective and maps ![]() $\tilde {\bigwedge }^2\mathbb {R}^+$ surjectively to the summand
$\tilde {\bigwedge }^2\mathbb {R}^+$ surjectively to the summand ![]() $K_2(\mathbb {R})$ in
$K_2(\mathbb {R})$ in ![]() $H_2(\mathrm {B} \mathrm {GL}_2^+(\mathbb {R})^{\delta }; \mathbb {Z})$. So we summarize what we need from Suslin's calculation in the following lemma.
$H_2(\mathrm {B} \mathrm {GL}_2^+(\mathbb {R})^{\delta }; \mathbb {Z})$. So we summarize what we need from Suslin's calculation in the following lemma.
Lemma 2.14 The map
surjects to the image of ![]() $K_2(\mathbb {R})\cong H_2(\mathrm {B}\widetilde {\mathrm {SL}_2}(\mathbb {R})^{\delta }; \mathbb {Z})\to H_2(\mathrm {B} \mathrm {GL}_2^+(\mathbb {R})^{\delta }; \mathbb {Z})$.
$K_2(\mathbb {R})\cong H_2(\mathrm {B}\widetilde {\mathrm {SL}_2}(\mathbb {R})^{\delta }; \mathbb {Z})\to H_2(\mathrm {B} \mathrm {GL}_2^+(\mathbb {R})^{\delta }; \mathbb {Z})$.
Proof Proof of Theorem 2.4
Since ![]() $X$ is simply connected, to prove that it is
$X$ is simply connected, to prove that it is ![]() $2$-connected, we need to show that
$2$-connected, we need to show that ![]() $H_2(X;\mathbb {Z})=0$. The homotopy pushout in diagram (2.2) gives the Mayer–Vietoris sequence
$H_2(X;\mathbb {Z})=0$. The homotopy pushout in diagram (2.2) gives the Mayer–Vietoris sequence
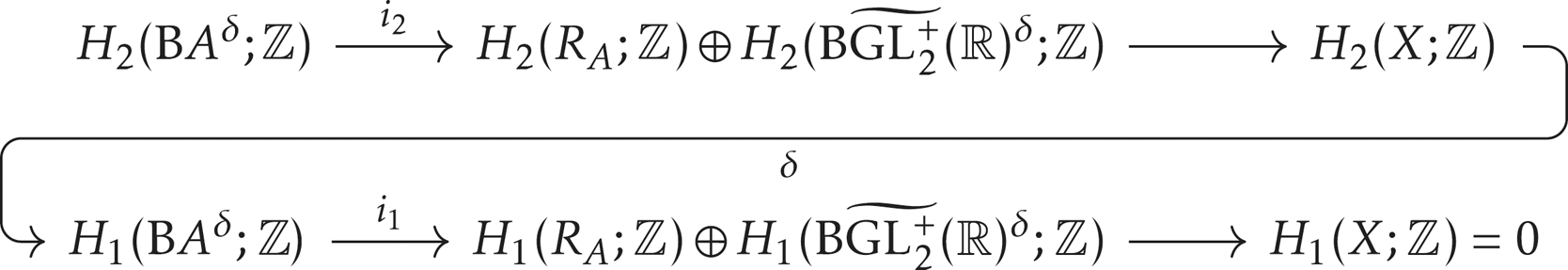
First, we observe that ![]() $i_1$ is an isomorphism. From Corollary 2.13, we know that the kernel of the map
$i_1$ is an isomorphism. From Corollary 2.13, we know that the kernel of the map
is given by the image of ![]() $H_1(\mathrm {B}\mathrm {Aff}^+(\mathbb {R})^{\delta }; \mathbb {Z})\to H_1(\mathrm {B}A^{\delta }; \mathbb {Z})$. So to prove that
$H_1(\mathrm {B}\mathrm {Aff}^+(\mathbb {R})^{\delta }; \mathbb {Z})\to H_1(\mathrm {B}A^{\delta }; \mathbb {Z})$. So to prove that ![]() $i_1$ is an isomorphism, it is enough to show the composition
$i_1$ is an isomorphism, it is enough to show the composition
induces an isomorphism on the first homology. On the other hand, using the isomorphism ![]() $f\colon \mathrm {SL}_2(\mathbb {R})\times \mathbb {R}^{+}\xrightarrow {\cong } \mathrm {GL}_2^+(\mathbb {R})$, we know that
$f\colon \mathrm {SL}_2(\mathbb {R})\times \mathbb {R}^{+}\xrightarrow {\cong } \mathrm {GL}_2^+(\mathbb {R})$, we know that
is an isomorphism. Hence, to prove that ![]() $i_1$ is an isomorphism, it is enough to show that
$i_1$ is an isomorphism, it is enough to show that
is an isomorphism. The Serre spectral sequence for the fibration
gives the long exact sequence
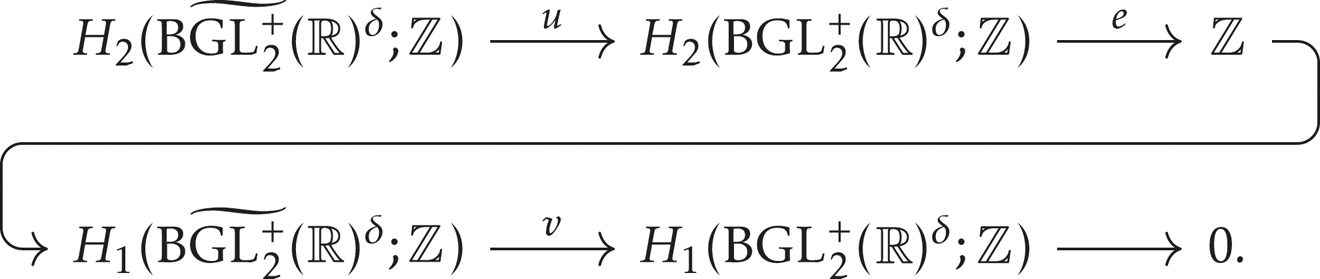
The map ![]() $e$ is the Euler class for flat
$e$ is the Euler class for flat ![]() $\mathrm {GL}_2^+(\mathbb {R})$-bundles over surfaces. By Milnor's theorem [Reference MilnorMil58, Theorem 2], the Euler number of flat
$\mathrm {GL}_2^+(\mathbb {R})$-bundles over surfaces. By Milnor's theorem [Reference MilnorMil58, Theorem 2], the Euler number of flat ![]() $\mathrm {GL}_2^+(\mathbb {R})$-bundles over a surface of genus
$\mathrm {GL}_2^+(\mathbb {R})$-bundles over a surface of genus ![]() $g$ can take any value between
$g$ can take any value between ![]() $-g+1$ and
$-g+1$ and ![]() $g-1$. So by varying
$g-1$. So by varying ![]() $g$, we conclude that
$g$, we conclude that ![]() $e$ is surjective (it is in fact split surjective). Therefore, the map
$e$ is surjective (it is in fact split surjective). Therefore, the map ![]() $v$ is an isomorphism.
$v$ is an isomorphism.
So to prove that ![]() $H_2(X;\mathbb {Z})=0$, it is enough to show that
$H_2(X;\mathbb {Z})=0$, it is enough to show that
is a surjection. In Corollary 2.13, we determined the kernel of the split surjective map
Hence, it is enough to show that ![]() $\ker (\alpha _2)\to H_2(\mathrm {B}\widetilde {\mathrm {GL}_2^+}(\mathbb {R})^{\delta }; \mathbb {Z})$ is surjective.
$\ker (\alpha _2)\to H_2(\mathrm {B}\widetilde {\mathrm {GL}_2^+}(\mathbb {R})^{\delta }; \mathbb {Z})$ is surjective.
Recall that
is split injective where ![]() $\mathrm {Im}(u)\cong K_2(\mathbb {R})\oplus \bigwedge ^2 \mathbb {R}^{+}$ and by the above discussion the co-kernel is isomorphic to
$\mathrm {Im}(u)\cong K_2(\mathbb {R})\oplus \bigwedge ^2 \mathbb {R}^{+}$ and by the above discussion the co-kernel is isomorphic to ![]() $\mathbb {Z}$ via the map
$\mathbb {Z}$ via the map ![]() $e$ in the long exact sequence (2.17). So we need to show that
$e$ in the long exact sequence (2.17). So we need to show that ![]() $\ker (\alpha _2)\cong (\mathbb {R}^+\otimes \mathbb {R}^+)\oplus \bigwedge ^2\mathbb {R}^+$ maps surjectively to the summand
$\ker (\alpha _2)\cong (\mathbb {R}^+\otimes \mathbb {R}^+)\oplus \bigwedge ^2\mathbb {R}^+$ maps surjectively to the summand ![]() $\mathrm {Im}(p)$.
$\mathrm {Im}(p)$.
Recall from Corollary 2.13 that the map ![]() $t\colon \mathbb {R}^+\to A$ given by
$t\colon \mathbb {R}^+\to A$ given by ![]() $t(a)=\big [\begin{smallmatrix} 1 & 0 \\ 0 & a \end{smallmatrix}\big ]$ induces a map on the second homology groups
$t(a)=\big [\begin{smallmatrix} 1 & 0 \\ 0 & a \end{smallmatrix}\big ]$ induces a map on the second homology groups
which is isomorphic to the summand ![]() $\bigwedge ^2 \mathbb {R}^{+}$ in
$\bigwedge ^2 \mathbb {R}^{+}$ in ![]() $\ker (\alpha _2)$ in Corollary 2.13. On other hand, under the isomorphism
$\ker (\alpha _2)$ in Corollary 2.13. On other hand, under the isomorphism ![]() $f\colon \mathrm {SL}_2(\mathbb {R})\times \mathbb {R}^{+}\xrightarrow {\cong } \mathrm {GL}_2^+(\mathbb {R})$, the matrix
$f\colon \mathrm {SL}_2(\mathbb {R})\times \mathbb {R}^{+}\xrightarrow {\cong } \mathrm {GL}_2^+(\mathbb {R})$, the matrix ![]() $t(a)$ comes from
$t(a)$ comes from ![]() $(\mathrm {Id}, \sqrt {a})$. Given that the square root is an isomorphism of
$(\mathrm {Id}, \sqrt {a})$. Given that the square root is an isomorphism of ![]() $\mathbb {R}^+$, we obtain that the composition of maps
$\mathbb {R}^+$, we obtain that the composition of maps
is injective and isomorphic to the summand ![]() $\bigwedge ^2 \mathbb {R}^{+}$. Hence, to finish the proof of surjectivity of
$\bigwedge ^2 \mathbb {R}^{+}$. Hence, to finish the proof of surjectivity of
it is enough to prove that the summand ![]() $\mathbb {R}^+\otimes \mathbb {R}^+$ in
$\mathbb {R}^+\otimes \mathbb {R}^+$ in ![]() $\ker (\alpha _2)$ maps surjectively to
$\ker (\alpha _2)$ maps surjectively to ![]() $K_2(\mathbb {R})$. Recall that the summand
$K_2(\mathbb {R})$. Recall that the summand ![]() $\mathbb {R}^+\otimes \mathbb {R}^+$ in Corollary 2.13 is induced by embedding of diagonal matrices and using the Kenneth formula
$\mathbb {R}^+\otimes \mathbb {R}^+$ in Corollary 2.13 is induced by embedding of diagonal matrices and using the Kenneth formula
So from Lemma 2.14, it follows that the summand ![]() $\mathbb {R}^+\otimes \mathbb {R}^+$ in
$\mathbb {R}^+\otimes \mathbb {R}^+$ in ![]() $\ker (\alpha _2)$ maps surjectively to
$\ker (\alpha _2)$ maps surjectively to ![]() $K_2(\mathbb {R})$.
$K_2(\mathbb {R})$.
Recall that we have natural maps ![]() $\nu \colon \mathrm {B}\Gamma _2^{\mathrm {PL}}\to \mathrm {B}\mathrm {PL}^+(\mathbb {R}^2)$ and
$\nu \colon \mathrm {B}\Gamma _2^{\mathrm {PL}}\to \mathrm {B}\mathrm {PL}^+(\mathbb {R}^2)$ and ![]() $\zeta \colon \mathrm {B}\mathrm {PL}^+(\mathbb {R}^2)\xrightarrow {\simeq }\mathrm {B}\mathrm {Homeo}^+(\mathbb {R}^2)\simeq \mathrm {B}S^1$. So they induce a map
$\zeta \colon \mathrm {B}\mathrm {PL}^+(\mathbb {R}^2)\xrightarrow {\simeq }\mathrm {B}\mathrm {Homeo}^+(\mathbb {R}^2)\simeq \mathrm {B}S^1$. So they induce a map
We think of the map ![]() $\psi$ as the map that classifies the normal bundle to codimension
$\psi$ as the map that classifies the normal bundle to codimension ![]() $2$ PL Haefliger structures as
$2$ PL Haefliger structures as ![]() $\mathbb {R}^2$-bundles. Therefore, to prove Theorem 1.2 which says that
$\mathbb {R}^2$-bundles. Therefore, to prove Theorem 1.2 which says that ![]() $\overline {\mathrm {B}\Gamma }_2^{\mathrm {PL}}$ is
$\overline {\mathrm {B}\Gamma }_2^{\mathrm {PL}}$ is ![]() $4$-connected, it is enough to prove the following result.
$4$-connected, it is enough to prove the following result.
Theorem 2.19 The map ![]() $\psi$ induces an isomorphism on
$\psi$ induces an isomorphism on ![]() $H_*(-;\mathbb {Z})$ for
$H_*(-;\mathbb {Z})$ for ![]() $*\leq 4$.
$*\leq 4$.
We need another preliminary lemma. In Greenberg's homotopy pushout diagram (2.3), there is a map ![]() $q\colon LX/\!\!/ S^1\to rX$ and also there is a natural map
$q\colon LX/\!\!/ S^1\to rX$ and also there is a natural map ![]() $p\colon LX/\!\!/ S^1\to \mathrm {B}S^1$ that classifies the universal circle bundle over the homotopy quotient
$p\colon LX/\!\!/ S^1\to \mathrm {B}S^1$ that classifies the universal circle bundle over the homotopy quotient ![]() $LX/\!\!/ S^1$. Since the map
$LX/\!\!/ S^1$. Since the map ![]() $S^1\hookrightarrow \mathrm {Homeo}_0(S^1)$ is a homotopy equivalence, we shall consider the following equivalent models for these maps:
$S^1\hookrightarrow \mathrm {Homeo}_0(S^1)$ is a homotopy equivalence, we shall consider the following equivalent models for these maps:
There is also the composition ![]() $\mathrm {Homeo}_0(S^1)\to \mathrm {Homeo}_0(D^2)\to \mathrm {Homeo}^+(\mathbb {R}^2)$ where the first map is the Alexander cone construction and the second map is the restriction to the identity. This inclusion induces a weak homotopy equivalence
$\mathrm {Homeo}_0(S^1)\to \mathrm {Homeo}_0(D^2)\to \mathrm {Homeo}^+(\mathbb {R}^2)$ where the first map is the Alexander cone construction and the second map is the restriction to the identity. This inclusion induces a weak homotopy equivalence
Lemma 2.20 The maps ![]() $\iota \circ p$ and
$\iota \circ p$ and ![]() $\psi \circ q$ induce the same map on homology.
$\psi \circ q$ induce the same map on homology.
Proof. This is already implicit in Greenberg's paper [Reference GreenbergGre92], but for the convenience of the reader we shall first recall the relevant object for this proof. As in Greenberg's paper [Reference GreenbergGre92, p. 188], let ![]() $P_0$ be the group of germs of orientation-preserving PL homeomorphisms of
$P_0$ be the group of germs of orientation-preserving PL homeomorphisms of ![]() $\mathbb {R}^2$ that fix the origin. Ghys and Sergiescu [Reference Ghys and SergiescuGS87, § 2] and Greenberg [Reference GreenbergGre92, Theorem 2.25 and Corollary 2.26] proved a general version of the Mather–Thurston homology isomorphism theorem for certain groupoids on the circle. As a result, there is a map
$\mathbb {R}^2$ that fix the origin. Ghys and Sergiescu [Reference Ghys and SergiescuGS87, § 2] and Greenberg [Reference GreenbergGre92, Theorem 2.25 and Corollary 2.26] proved a general version of the Mather–Thurston homology isomorphism theorem for certain groupoids on the circle. As a result, there is a map
that induces a homology isomorphism. To prove the lemma, we use Greenberg's description of the Ghys–Sergiescu theorem to show that the two maps
induce isomorphic ![]() $\mathbb {R}^2$-bundles over
$\mathbb {R}^2$-bundles over ![]() $\mathrm {B}P_0$.
$\mathrm {B}P_0$.
By Greenberg's description [Reference GreenbergGre92, § 2.22], the composition ![]() $q\circ f\colon \mathrm {B}P_0\to \mathrm {B}\Gamma _2^{\mathrm {PL}}$ is induced by the inclusion of
$q\circ f\colon \mathrm {B}P_0\to \mathrm {B}\Gamma _2^{\mathrm {PL}}$ is induced by the inclusion of ![]() $P_0$ as the group of germs into the groupoid
$P_0$ as the group of germs into the groupoid ![]() $\Gamma _2^{\mathrm {PL}}$. One can canonically extend each germ in
$\Gamma _2^{\mathrm {PL}}$. One can canonically extend each germ in ![]() $P_0$ to a PL homeomorphism of
$P_0$ to a PL homeomorphism of ![]() $\mathbb {R}^2$. So there is a natural action of
$\mathbb {R}^2$. So there is a natural action of ![]() $P_0$ on
$P_0$ on ![]() $\mathbb {R}^2$. Therefore, the map
$\mathbb {R}^2$. Therefore, the map ![]() $\psi \circ q\circ f$,
$\psi \circ q\circ f$,
classifies the ![]() $\mathbb {R}^2$-bundle on
$\mathbb {R}^2$-bundle on ![]() $\mathrm {B}P_0$ induced by the action of
$\mathrm {B}P_0$ induced by the action of ![]() $P_0$ on
$P_0$ on ![]() $\mathbb {R}^2$.
$\mathbb {R}^2$.
On the other hand, ![]() $P_0$ acts on rays out of the origin. So
$P_0$ acts on rays out of the origin. So ![]() $P_0$ also maps into
$P_0$ also maps into ![]() $\mathrm {PP}(S^1)$ the group of orientation-preserving piecewise projective homeomorphisms of
$\mathrm {PP}(S^1)$ the group of orientation-preserving piecewise projective homeomorphisms of ![]() $S^1$. In particular, it is a subgroup of orientation-preserving homeomorphisms of the circle. The map
$S^1$. In particular, it is a subgroup of orientation-preserving homeomorphisms of the circle. The map ![]() $p\circ f$,
$p\circ f$,
classifies the natural circle bundle over ![]() $\mathrm {B}P_0$ induced by the action of
$\mathrm {B}P_0$ induced by the action of ![]() $P_0$ on
$P_0$ on ![]() $S^1$. Therefore, the map
$S^1$. Therefore, the map ![]() $\iota \circ p\circ f$ classifies the Euclidean
$\iota \circ p\circ f$ classifies the Euclidean ![]() $\mathbb {R}^2$-bundle induced by the natural action of
$\mathbb {R}^2$-bundle induced by the natural action of ![]() $P_0$ on
$P_0$ on ![]() $\mathbb {R}^2$.
$\mathbb {R}^2$.
Let ![]() $\mathrm {ev}\colon LX\to X$ be the map induced by evaluating loops at the base point
$\mathrm {ev}\colon LX\to X$ be the map induced by evaluating loops at the base point ![]() $1$ of the unit circle in the complex plane. The circle action
$1$ of the unit circle in the complex plane. The circle action ![]() $\eta \colon S^1\times LX\to LX$ sends the pair
$\eta \colon S^1\times LX\to LX$ sends the pair ![]() $(s, \gamma (t))$ where
$(s, \gamma (t))$ where ![]() $\gamma (t)$ is a free loop in
$\gamma (t)$ is a free loop in ![]() $X$ to the loop
$X$ to the loop ![]() $\gamma (st)$. The map
$\gamma (st)$. The map ![]() $\eta$ induces the map
$\eta$ induces the map
For each positive integer ![]() $k$, let
$k$, let ![]() $h_k\colon \pi _k(\Omega X)\to H_{k+1}(X; \mathbb {Z})$ be the map that sends the homotopy class of
$h_k\colon \pi _k(\Omega X)\to H_{k+1}(X; \mathbb {Z})$ be the map that sends the homotopy class of ![]() $f\colon S^k\to \Omega X$ to
$f\colon S^k\to \Omega X$ to ![]() $F_*([S^1\times S^k])$, where
$F_*([S^1\times S^k])$, where ![]() $F\colon S^1\times S^k\to X$ is the map induced by the adjoint of
$F\colon S^1\times S^k\to X$ is the map induced by the adjoint of ![]() $f$ (it is the adjoint of
$f$ (it is the adjoint of ![]() $f$ composed with swapping
$f$ composed with swapping ![]() $S^1$ and
$S^1$ and ![]() $S^k$ factors).
$S^k$ factors).
Lemma 2.21 We have a commutative diagram
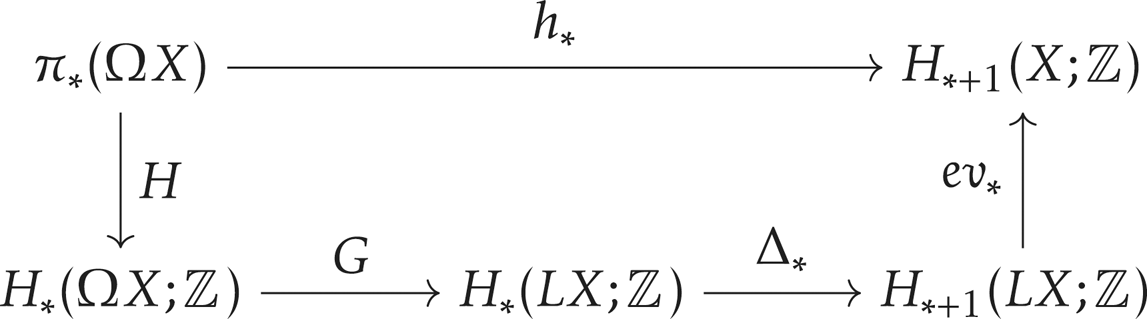
where the map ![]() $H$ is the Hurewicz map and the map
$H$ is the Hurewicz map and the map ![]() $G$ is induced by the inclusion
$G$ is induced by the inclusion ![]() $\Omega X\to LX$.
$\Omega X\to LX$.
Proof. Let ![]() $f\colon S^k\to \Omega X$ be an element in
$f\colon S^k\to \Omega X$ be an element in ![]() $\pi _k(\Omega X)$ and let
$\pi _k(\Omega X)$ and let ![]() $\tilde {f}$ be
$\tilde {f}$ be ![]() $G\circ H(f)\in H_k(LX;\mathbb {Z})$. Then
$G\circ H(f)\in H_k(LX;\mathbb {Z})$. Then ![]() $\Delta _k(\tilde {f})$ is defined to be the map
$\Delta _k(\tilde {f})$ is defined to be the map
which sends the pair ![]() $(s, x)$ to the action of
$(s, x)$ to the action of ![]() $s$ on the loop
$s$ on the loop ![]() $f(x)(t)$ which is
$f(x)(t)$ which is ![]() $f(x)(st)$. The evaluation map evaluates this loop at
$f(x)(st)$. The evaluation map evaluates this loop at ![]() $t=1$ which gives the same map as the adjoint
$t=1$ which gives the same map as the adjoint ![]() $F\colon S^1\times S^k\to X$. Hence, we have
$F\colon S^1\times S^k\to X$. Hence, we have ![]() $\mathrm {ev}_k\circ \Delta _k(\tilde {f})=h_k(f)$.
$\mathrm {ev}_k\circ \Delta _k(\tilde {f})=h_k(f)$.
Corollary 2.22 Let ![]() $X$ be a
$X$ be a ![]() $2$-connected space.
$2$-connected space.
• The map
 $\Delta _2$ is injective and
$\Delta _2$ is injective and  $\Delta _2(H_2(LX; \mathbb {Z}))$ maps isomorphically to
$\Delta _2(H_2(LX; \mathbb {Z}))$ maps isomorphically to  $H_3(X; \mathbb {Z})$ via the evaluation map
$H_3(X; \mathbb {Z})$ via the evaluation map  $\mathrm {ev}$.
$\mathrm {ev}$.•
 $\Delta _3(H_3(LX; \mathbb {Z}))$ maps surjectively to
$\Delta _3(H_3(LX; \mathbb {Z}))$ maps surjectively to  $H_4(X; \mathbb {Z})$ via the evaluation map
$H_4(X; \mathbb {Z})$ via the evaluation map  $\mathrm {ev}$.
$\mathrm {ev}$.
Proof. Since ![]() $X$ is
$X$ is ![]() $2$-connected, the Hurewicz map
$2$-connected, the Hurewicz map ![]() $\pi _3(X)\to H_3(X;\mathbb {Z})$ is an isomorphism and also
$\pi _3(X)\to H_3(X;\mathbb {Z})$ is an isomorphism and also ![]() $\pi _4(X)\to H_4(X; \mathbb {Z})$ is surjective. On the other hand,
$\pi _4(X)\to H_4(X; \mathbb {Z})$ is surjective. On the other hand, ![]() $LX$ is also simply connected, therefore we have the isomorphisms
$LX$ is also simply connected, therefore we have the isomorphisms
where ![]() $\Omega X$ is the based loop space on
$\Omega X$ is the based loop space on ![]() $X$. Also, note that the map
$X$. Also, note that the map
is an isomorphism. From Lemma 2.21, we know that ![]() $\mathrm {ev}_2\circ \Delta _2\colon \pi _2(\Omega X)\to H_3(X; \mathbb {Z})$ is the same map as
$\mathrm {ev}_2\circ \Delta _2\colon \pi _2(\Omega X)\to H_3(X; \mathbb {Z})$ is the same map as ![]() $h_2$, which proves the first statement.
$h_2$, which proves the first statement.
Since ![]() $\Omega X$ is simply connected, the Hurewicz map
$\Omega X$ is simply connected, the Hurewicz map
is surjective. So to prove the second statement, it is enough to show that the composition
is surjective. But again by Lemma 2.21 the above composition is the same as the natural map
that sends the homotopy class of ![]() $f\colon S^3\to \Omega X$ to
$f\colon S^3\to \Omega X$ to ![]() $F_*([S^1\times S^3])$, where
$F_*([S^1\times S^3])$, where ![]() $F\colon S^1\times S^3\to X$ is the map induced by the adjoint of
$F\colon S^1\times S^3\to X$ is the map induced by the adjoint of ![]() $f$. Now since
$f$. Now since ![]() $X$ is
$X$ is ![]() $2$-connected, the map
$2$-connected, the map ![]() $h_3$ is surjective. Therefore, the composition (2.23) is also surjective.
$h_3$ is surjective. Therefore, the composition (2.23) is also surjective.
Proof Proof of Theorem 2.19
Recall from the introduction that the space ![]() $\overline {\mathrm {B}\Gamma }_2^{\mathrm {PL}}$, which is weakly equivalent to the homotopy fiber of the map
$\overline {\mathrm {B}\Gamma }_2^{\mathrm {PL}}$, which is weakly equivalent to the homotopy fiber of the map
is known to be at least ![]() $2$-connected. So the map
$2$-connected. So the map ![]() $\psi$ induces isomorphisms on
$\psi$ induces isomorphisms on ![]() $H_*(-;\mathbb {Z})$ for
$H_*(-;\mathbb {Z})$ for ![]() $*\leq 2$. Hence, we need to show two things; one is that
$*\leq 2$. Hence, we need to show two things; one is that ![]() $H_3(rX; \mathbb {Z})=0$ and the other is that
$H_3(rX; \mathbb {Z})=0$ and the other is that
is an isomorphism. First, note that the Mayer–Vietoris sequence for the pushout (2.3) gives
To compute ![]() $H_*(rX;\mathbb {Z})$ for
$H_*(rX;\mathbb {Z})$ for ![]() $*\leq 4$, we use that
$*\leq 4$, we use that ![]() $X$ is
$X$ is ![]() $2$-connected and the fact that fibrations
$2$-connected and the fact that fibrations
 $$ \begin{gathered} \Omega
X\to LX\xrightarrow{\textrm{ev}} X,\\ LX\to LX/\!\!/
S^1\xrightarrow{p} \textrm{B}S^1 \end{gathered} $$
$$ \begin{gathered} \Omega
X\to LX\xrightarrow{\textrm{ev}} X,\\ LX\to LX/\!\!/
S^1\xrightarrow{p} \textrm{B}S^1 \end{gathered} $$
have sections. The first fibration has a section by considering constant loops and the second fibration has a section because the action of ![]() $S^1$ has fixed points, that is, the constant loops. Therefore,
$S^1$ has fixed points, that is, the constant loops. Therefore, ![]() $H_*(LX)\xrightarrow {\mathrm {ev}_*}H_*(X)$ is surjective and so is
$H_*(LX)\xrightarrow {\mathrm {ev}_*}H_*(X)$ is surjective and so is ![]() $H_*(LX/\!\!/ S^1)\to H_*(\mathrm {B}S^1)$, and since they have sections,
$H_*(LX/\!\!/ S^1)\to H_*(\mathrm {B}S^1)$, and since they have sections, ![]() $H_*(X)$ and
$H_*(X)$ and ![]() $H_*(\mathrm {B}S^1)$ split off as summands from
$H_*(\mathrm {B}S^1)$ split off as summands from ![]() $H_*(LX)$ and
$H_*(LX)$ and ![]() $H_*(LX/\!\!/ S^1)$, respectively.
$H_*(LX/\!\!/ S^1)$, respectively.
From the Serre spectral sequence for the fibration (2.24), we see that ![]() $H_2(LX; \mathbb {Z})\to H_2(LX/\!\!/ S^1; \mathbb {Z})$ is injective. So to show that
$H_2(LX; \mathbb {Z})\to H_2(LX/\!\!/ S^1; \mathbb {Z})$ is injective. So to show that ![]() $H_3(rX; \mathbb {Z})=0$, it is enough to prove that
$H_3(rX; \mathbb {Z})=0$, it is enough to prove that
is surjective.
Note that the differentials of the spectral sequence out of the terms isomorphic to ![]() $\mathbb {Z}$s in the
$\mathbb {Z}$s in the ![]() $0$th row are trivial because of the existence of the section for the map
$0$th row are trivial because of the existence of the section for the map ![]() $p$ in fibration (2.24). And it is standard that the differentials
$p$ in fibration (2.24). And it is standard that the differentials
are the same as the map ![]() $\Delta _i$ in Corollary 2.22 [Reference Bökstedt and OttosenBO99, Proposition 3.3].
$\Delta _i$ in Corollary 2.22 [Reference Bökstedt and OttosenBO99, Proposition 3.3].
From the first part of Corollary 2.22, we know that the map ![]() $d_2$ in
$d_2$ in
is injective and the natural map ![]() $\mathrm {ev}_*\colon d_2(H_2(LX; \mathbb {Z}))\to H_3(X; \mathbb {Z})$ is an isomorphism. Given that
$\mathrm {ev}_*\colon d_2(H_2(LX; \mathbb {Z}))\to H_3(X; \mathbb {Z})$ is an isomorphism. Given that ![]() $d_2(H_2(LX; \mathbb {Z}))$ is the kernel of the surjection
$d_2(H_2(LX; \mathbb {Z}))$ is the kernel of the surjection ![]() $H_3(LX)\twoheadrightarrow H_3(LX/\!\!/ S^1)$, the map (2.25) is in fact an isomorphism. So we have
$H_3(LX)\twoheadrightarrow H_3(LX/\!\!/ S^1)$, the map (2.25) is in fact an isomorphism. So we have ![]() $H_3(rX; \mathbb {Z})=0$.
$H_3(rX; \mathbb {Z})=0$.
Now since the map (2.25) is an isomorphism, to show that ![]() $\psi$ induces an isomorphism on
$\psi$ induces an isomorphism on ![]() $H_4(-;\mathbb {Z})$ it is enough to show that the co-kernel of the map
$H_4(-;\mathbb {Z})$ it is enough to show that the co-kernel of the map
is the ![]() $\mathbb {Z}$ summand in
$\mathbb {Z}$ summand in ![]() $H_4(LX/\!\!/ S^1; \mathbb {Z})$ coming from the
$H_4(LX/\!\!/ S^1; \mathbb {Z})$ coming from the ![]() $0$th row in the Serre spectral sequence. This is because, in that case, the composition
$0$th row in the Serre spectral sequence. This is because, in that case, the composition
where the first map is the section of ![]() $p$, induces an isomorphism on
$p$, induces an isomorphism on ![]() $H_4(-;\mathbb {Z})$; and Lemma 2.20 implies that the composition
$H_4(-;\mathbb {Z})$; and Lemma 2.20 implies that the composition
induces a homology isomorphism.
To do this, from the second part of Corollary 2.22, we know that, in
![]() $d_2(H_3(LX; \mathbb {Z}))$ surjects to
$d_2(H_3(LX; \mathbb {Z}))$ surjects to ![]() $H_4(X; \mathbb {Z})$ via
$H_4(X; \mathbb {Z})$ via ![]() $\mathrm {ev}_*$. Since
$\mathrm {ev}_*$. Since ![]() $H_4(LX/\!\!/ S^1; \mathbb {Z})$ is isomorphic to
$H_4(LX/\!\!/ S^1; \mathbb {Z})$ is isomorphic to ![]() $\mathbb {Z}\oplus H_4(LX; \mathbb {Z})/d_2(H_3(LX; \mathbb {Z}))$, the co-kernel of the map
$\mathbb {Z}\oplus H_4(LX; \mathbb {Z})/d_2(H_3(LX; \mathbb {Z}))$, the co-kernel of the map
is the ![]() $\mathbb {Z}$ summand in
$\mathbb {Z}$ summand in ![]() $H_4(LX/\!\!/ S^1; \mathbb {Z})$. Hence,
$H_4(LX/\!\!/ S^1; \mathbb {Z})$. Hence, ![]() $\psi$ induces an isomorphism on
$\psi$ induces an isomorphism on ![]() $H_4(-;\mathbb {Z})$.
$H_4(-;\mathbb {Z})$.
Question 2.11 Is there a ‘discrete’ Godbillon–Vey class similar to the case codimension ![]() $1$ PL foliations in [Reference Ghys and SergiescuGS87], to give a nontrivial map
$1$ PL foliations in [Reference Ghys and SergiescuGS87], to give a nontrivial map ![]() $H_5(\overline {\mathrm {B}\Gamma }_2^{\mathrm {PL}};\mathbb {Z})\to \mathbb {R}$?
$H_5(\overline {\mathrm {B}\Gamma }_2^{\mathrm {PL}};\mathbb {Z})\to \mathbb {R}$?
2.2 Homology of PL surface homeomorphisms made discrete
To relate the group homology of PL surface homeomorphisms to the homotopy type of ![]() $\overline {\mathrm {B}\Gamma }_2^{\mathrm {PL}}$, we first recall a version of the Mather–Thurston theorem that the author proved [Reference NarimanNar23, § 5]. Let
$\overline {\mathrm {B}\Gamma }_2^{\mathrm {PL}}$, we first recall a version of the Mather–Thurston theorem that the author proved [Reference NarimanNar23, § 5]. Let ![]() $M$ be an
$M$ be an ![]() $n$-dimensional PL manifold possibly with a nonempty boundary. The topological group
$n$-dimensional PL manifold possibly with a nonempty boundary. The topological group ![]() $\mathrm {PL}(M, \mathrm {rel}\,\partial )$ is the realization of the simplicial group
$\mathrm {PL}(M, \mathrm {rel}\,\partial )$ is the realization of the simplicial group ![]() $S_{\bullet }\mathrm {PL}(M, \mathrm {rel}\,\partial )$ whose
$S_{\bullet }\mathrm {PL}(M, \mathrm {rel}\,\partial )$ whose ![]() $k$-simplices are given by the set of PL homeomorphisms of
$k$-simplices are given by the set of PL homeomorphisms of ![]() $\Delta ^k\times M$ that commute with the projection to the first factor and whose supports are away from the boundary of
$\Delta ^k\times M$ that commute with the projection to the first factor and whose supports are away from the boundary of ![]() $M$. We have the map
$M$. We have the map ![]() $\mathrm {PL}(M, \mathrm {rel}\,\partial )^{\delta }\to \mathrm {PL}(M, \mathrm {rel}\,\partial )$ given by the inclusion of
$\mathrm {PL}(M, \mathrm {rel}\,\partial )^{\delta }\to \mathrm {PL}(M, \mathrm {rel}\,\partial )$ given by the inclusion of ![]() $0$-simplices. This map induces the map between classifying spaces
$0$-simplices. This map induces the map between classifying spaces
whose homotopy fiber is denoted by ![]() $\overline {\mathrm {B}\mathrm {PL}(M, \mathrm {rel}\,\partial )}$. This homotopy fiber can also be described as the realization of the semi-simplicial set
$\overline {\mathrm {B}\mathrm {PL}(M, \mathrm {rel}\,\partial )}$. This homotopy fiber can also be described as the realization of the semi-simplicial set ![]() $S_{\bullet }(\overline {\mathrm {B}\mathrm {PL}(M, \mathrm {rel}\,\partial )})$ whose
$S_{\bullet }(\overline {\mathrm {B}\mathrm {PL}(M, \mathrm {rel}\,\partial )})$ whose ![]() $k$-simplices are given by the set of codimension
$k$-simplices are given by the set of codimension ![]() $n$ foliations on
$n$ foliations on ![]() $\Delta ^k \times M$ that are transverse to the fibers of the projection
$\Delta ^k \times M$ that are transverse to the fibers of the projection ![]() $\Delta ^k\times M\to \Delta ^k$ and the holonomies are compactly supported PL homeomorphisms of the fiber
$\Delta ^k\times M\to \Delta ^k$ and the holonomies are compactly supported PL homeomorphisms of the fiber ![]() $M$. Note that
$M$. Note that ![]() $S_{\bullet }\mathrm {PL}(M, \mathrm {rel}\,\partial )$ acts levelwise on the simplices
$S_{\bullet }\mathrm {PL}(M, \mathrm {rel}\,\partial )$ acts levelwise on the simplices ![]() $S_{\bullet }(\overline {\mathrm {B}\mathrm {PL}(M, \mathrm {rel}\,\partial )})$. Hence, we have an action of
$S_{\bullet }(\overline {\mathrm {B}\mathrm {PL}(M, \mathrm {rel}\,\partial )})$. Hence, we have an action of ![]() $\mathrm {PL}(M, \mathrm {rel}\,\partial )$ on
$\mathrm {PL}(M, \mathrm {rel}\,\partial )$ on ![]() $\overline {\mathrm {B}\mathrm {PL}(M, \mathrm {rel}\,\partial )}$.
$\overline {\mathrm {B}\mathrm {PL}(M, \mathrm {rel}\,\partial )}$.
On the other hand, the space ![]() $\overline {\mathrm {B}\mathrm {PL}(M, \mathrm {rel}\,\partial )}$ is related to the classifying space of the groupoid
$\overline {\mathrm {B}\mathrm {PL}(M, \mathrm {rel}\,\partial )}$ is related to the classifying space of the groupoid ![]() $\Gamma _n^{\mathrm {PL}}$ as follows. Recall that forgetting the germ of the foliation of foliated microbundles induces the map
$\Gamma _n^{\mathrm {PL}}$ as follows. Recall that forgetting the germ of the foliation of foliated microbundles induces the map
between classifying spaces. Let ![]() $\tau _M\colon M\to \mathrm {B}\mathrm {PL}(\mathbb {R}^n)$ be a map that classifies the tangent microbundle of
$\tau _M\colon M\to \mathrm {B}\mathrm {PL}(\mathbb {R}^n)$ be a map that classifies the tangent microbundle of ![]() $M$. Let
$M$. Let ![]() $\mathrm {Sect}_{\partial }(\tau _M^*(\nu ))$ be the space of sections of the pullback bundle
$\mathrm {Sect}_{\partial }(\tau _M^*(\nu ))$ be the space of sections of the pullback bundle ![]() $\tau _M^*(\nu )$ over
$\tau _M^*(\nu )$ over ![]() $M$ that are supported away from the boundary. The support of a section is measured with respect to a fixed base section. By the obstruction theory and the fact that the fiber of the bundle
$M$ that are supported away from the boundary. The support of a section is measured with respect to a fixed base section. By the obstruction theory and the fact that the fiber of the bundle ![]() $\tau _M^*(\nu )$ over
$\tau _M^*(\nu )$ over ![]() $M$ is at least
$M$ is at least ![]() $n$-connected, the space of sections is connected. So different choices of a base section do not change the homotopy type of the compactly supported sections.
$n$-connected, the space of sections is connected. So different choices of a base section do not change the homotopy type of the compactly supported sections.
We recall from [Reference NarimanNar17, § 1.2.2] how ![]() $\mathrm {PL}(M, \mathrm {rel}\,\partial )$ acts on
$\mathrm {PL}(M, \mathrm {rel}\,\partial )$ acts on ![]() $\mathrm {Sect}_{\partial }(\tau _M^*(\nu ))$. The PL tangent microbundle of the PL manifold
$\mathrm {Sect}_{\partial }(\tau _M^*(\nu ))$. The PL tangent microbundle of the PL manifold ![]() $M$ is the microbundle
$M$ is the microbundle
A germ of PL foliation ![]() $c$ on
$c$ on ![]() $\Delta ^p\times M\times M$ at
$\Delta ^p\times M\times M$ at ![]() $\Delta ^p\times \mathrm {diag }M$ which is transverse to the fiber of the projection
$\Delta ^p\times \mathrm {diag }M$ which is transverse to the fiber of the projection ![]() $id\times pr_1: \Delta ^p\times M\times M\to \Delta ^p\times M$ is said to be horizontal at
$id\times pr_1: \Delta ^p\times M\times M\to \Delta ^p\times M$ is said to be horizontal at ![]() $x\in M$ if there exists a neighborhood
$x\in M$ if there exists a neighborhood ![]() $U$ around
$U$ around ![]() $x$ such that the restriction of the foliation
$x$ such that the restriction of the foliation ![]() $c$ to
$c$ to ![]() $\Delta ^p\times U\times U$ is induced by the projection
$\Delta ^p\times U\times U$ is induced by the projection ![]() $\Delta ^p\times U\times U\to U$ on the last factor. By the support of
$\Delta ^p\times U\times U\to U$ on the last factor. By the support of ![]() $c$ we mean the set of
$c$ we mean the set of ![]() $x\in M$ where
$x\in M$ where ![]() $c$ is not horizontal.
$c$ is not horizontal.
Now we define the semi-simplicial set ![]() $S_{\bullet }( \mathrm {Sect}_c(\tau _M^*(\nu )))$ whose
$S_{\bullet }( \mathrm {Sect}_c(\tau _M^*(\nu )))$ whose ![]() $p$-simplices are given as the set of germs of PL foliations on
$p$-simplices are given as the set of germs of PL foliations on ![]() $\Delta ^p\times M\times M$ at
$\Delta ^p\times M\times M$ at ![]() $\Delta ^p\times \mathrm {diag }M$ which are transverse to the fiber of the projection
$\Delta ^p\times \mathrm {diag }M$ which are transverse to the fiber of the projection ![]() $id\times pr_1: \Delta ^p\times M\times M\to \Delta ^p\times M$ and have compact support. The realization of this semi-simplicial set gives a model for the compactly supported sections
$id\times pr_1: \Delta ^p\times M\times M\to \Delta ^p\times M$ and have compact support. The realization of this semi-simplicial set gives a model for the compactly supported sections ![]() $\mathrm {Sect}_c(\tau _M^*(\nu ))$. Similarly to the previous case, there is an obvious action of
$\mathrm {Sect}_c(\tau _M^*(\nu ))$. Similarly to the previous case, there is an obvious action of ![]() $S_{\bullet }(\mathrm {PL}(M, \mathrm {rel}\,\partial ))$ on
$S_{\bullet }(\mathrm {PL}(M, \mathrm {rel}\,\partial ))$ on ![]() $S_{\bullet }( \mathrm {Sect}_c(\tau _M^*(\nu )))$.
$S_{\bullet }( \mathrm {Sect}_c(\tau _M^*(\nu )))$.
In this model, there is a natural map [Reference NarimanNar17, § 1.2.2]
that is ![]() $\mathrm {PL}(M, \mathrm {rel}\,\partial )$-equivariant, and we showed that it induces a homology isomorphism [Reference NarimanNar23].Footnote 2 Therefore, the induced map between the homotopy quotients of the actions of
$\mathrm {PL}(M, \mathrm {rel}\,\partial )$-equivariant, and we showed that it induces a homology isomorphism [Reference NarimanNar23].Footnote 2 Therefore, the induced map between the homotopy quotients of the actions of ![]() $\mathrm {PL}(M, \mathrm {rel}\,\partial )$ on both sides also induces a homology isomorphism. Hence,
$\mathrm {PL}(M, \mathrm {rel}\,\partial )$ on both sides also induces a homology isomorphism. Hence, ![]() $\mathrm {B}{\mathrm {PL}}^{\delta }(M,\mathrm {rel}\,\partial )$ is homology isomorphic to
$\mathrm {B}{\mathrm {PL}}^{\delta }(M,\mathrm {rel}\,\partial )$ is homology isomorphic to ![]() $\mathrm {Sect}_{\partial }(\tau _M^*(\nu ))/\!\!/ \mathrm {PL}(M, \mathrm {rel}\,\partial )$.
$\mathrm {Sect}_{\partial }(\tau _M^*(\nu ))/\!\!/ \mathrm {PL}(M, \mathrm {rel}\,\partial )$.
Proof Proof of Theorem 1.5
Let ![]() $\Sigma$ be an oriented closed surface possibly with nonempty boundary. To show that the map
$\Sigma$ be an oriented closed surface possibly with nonempty boundary. To show that the map
induces an isomorphism on ![]() $H_*(-;\mathbb {Z})$ for
$H_*(-;\mathbb {Z})$ for ![]() $*\leq 2$ and a surjection on
$*\leq 2$ and a surjection on ![]() $H_3(-;\mathbb {Z})$, it is enough to show that
$H_3(-;\mathbb {Z})$, it is enough to show that ![]() $H_*(\overline { \mathrm {B}{\mathrm {PL}}(\Sigma,\mathrm {rel}\,\partial )};\mathbb {Z})$ vanishes for
$H_*(\overline { \mathrm {B}{\mathrm {PL}}(\Sigma,\mathrm {rel}\,\partial )};\mathbb {Z})$ vanishes for ![]() $*\leq 2$. By the Mather–Thurston theorem described above, these groups are isomorphic to
$*\leq 2$. By the Mather–Thurston theorem described above, these groups are isomorphic to ![]() $H_*(\mathrm {Sect}_{\partial }(\tau _{\Sigma }^*(\nu ));\mathbb {Z})$. Hence, it is enough to show that
$H_*(\mathrm {Sect}_{\partial }(\tau _{\Sigma }^*(\nu ));\mathbb {Z})$. Hence, it is enough to show that ![]() $\mathrm {Sect}_{\partial }(\tau _{\Sigma }^*(\nu ))$ is
$\mathrm {Sect}_{\partial }(\tau _{\Sigma }^*(\nu ))$ is ![]() $2$-connected. Note that, in general, if the fiber of a fibration
$2$-connected. Note that, in general, if the fiber of a fibration ![]() $\pi \colon E\to M^n$ is
$\pi \colon E\to M^n$ is ![]() $k$-connected, elementary obstruction theory argument implies that the space of section of
$k$-connected, elementary obstruction theory argument implies that the space of section of ![]() $\pi$ is
$\pi$ is ![]() $(k-n)$-connected. Now recall that the homotopy fiber of the fibration
$(k-n)$-connected. Now recall that the homotopy fiber of the fibration ![]() $\tau _{\Sigma }^*(\nu )\to \Sigma$ is
$\tau _{\Sigma }^*(\nu )\to \Sigma$ is ![]() $\overline {\mathrm {B}\Gamma }_2^{\mathrm {PL}}$ which is
$\overline {\mathrm {B}\Gamma }_2^{\mathrm {PL}}$ which is ![]() $4$-connected by Theorem 1.2. Therefore, the space
$4$-connected by Theorem 1.2. Therefore, the space ![]() $\mathrm {Sect}_{\partial }(\tau _{\Sigma }^*(\nu ))$ is
$\mathrm {Sect}_{\partial }(\tau _{\Sigma }^*(\nu ))$ is ![]() $2$-connected.
$2$-connected.
Remark 2.29 Calegari and Rolfsen proved in particular the local indicability of PL homeomorphisms [Reference Calegari and RolfsenCR15, Theorem 3.3.1] of manifolds relative to the nonempty boundary. As a consequence of their local indicability result, one deduces that no finitely generated subgroup of ![]() ${\mathrm {PL}}^{\delta }_{c,0}(\Sigma )$ is a simple group. However, our theorem shows that the ambient group
${\mathrm {PL}}^{\delta }_{c,0}(\Sigma )$ is a simple group. However, our theorem shows that the ambient group ![]() ${\mathrm {PL}}^{\delta }_{c,0}(\Sigma )$ is simple, which is similar to Thurston's stability for
${\mathrm {PL}}^{\delta }_{c,0}(\Sigma )$ is simple, which is similar to Thurston's stability for ![]() $C^1$-diffeomorphisms groups [Reference ThurstonThu74c].
$C^1$-diffeomorphisms groups [Reference ThurstonThu74c].
Remark 2.30 We know that ![]() ${\mathrm {PL}}_0(\Sigma,\mathrm {rel}\,\partial )\simeq \mathrm {Diff}_0(\Sigma,\mathrm {rel}\,\partial )$ [Reference Balcerak and HajdukBH81, p. 8]. Given that the homotopy type of
${\mathrm {PL}}_0(\Sigma,\mathrm {rel}\,\partial )\simeq \mathrm {Diff}_0(\Sigma,\mathrm {rel}\,\partial )$ [Reference Balcerak and HajdukBH81, p. 8]. Given that the homotopy type of ![]() $\mathrm {Diff}_0(\Sigma,\mathrm {rel}\,\partial )$ is completely known for all surfaces [Reference Earle and EellsEE69], we could also compute the second group homology of
$\mathrm {Diff}_0(\Sigma,\mathrm {rel}\,\partial )$ is completely known for all surfaces [Reference Earle and EellsEE69], we could also compute the second group homology of ![]() ${\mathrm {PL}}^{\delta }_0(\Sigma,\mathrm {rel}\,\partial )$ with
${\mathrm {PL}}^{\delta }_0(\Sigma,\mathrm {rel}\,\partial )$ with ![]() $\mathbb {F}_p$ coefficients. For example, if
$\mathbb {F}_p$ coefficients. For example, if ![]() $\Sigma$ is a hyperbolic surface, we obtain that
$\Sigma$ is a hyperbolic surface, we obtain that ![]() $H_2(\mathrm {B}{\mathrm {PL}}^{\delta }_0(\Sigma,\mathrm {rel}\,\partial );\mathbb {Z})$ is trivial.
$H_2(\mathrm {B}{\mathrm {PL}}^{\delta }_0(\Sigma,\mathrm {rel}\,\partial );\mathbb {Z})$ is trivial.
In this dimension, it is known [Reference Balcerak and HajdukBH81, p. 8] that ![]() $\mathrm {PL}^+(\mathbb {R}^2)\simeq \mathrm {SO}(2)$. Therefore,
$\mathrm {PL}^+(\mathbb {R}^2)\simeq \mathrm {SO}(2)$. Therefore, ![]() $H^*( \mathrm {B}\mathrm {PL}^+(\mathbb {R}^2);$
$H^*( \mathrm {B}\mathrm {PL}^+(\mathbb {R}^2);$ ![]() $\mathbb {Q})$ is generated by the Euler class
$\mathbb {Q})$ is generated by the Euler class ![]() $e\in H^2(\mathrm {B}\mathrm {PL}^+(\mathbb {R}^2);\mathbb {Q})$. A consequence of our computation with Greenberg's model is the following nonvanishing result.
$e\in H^2(\mathrm {B}\mathrm {PL}^+(\mathbb {R}^2);\mathbb {Q})$. A consequence of our computation with Greenberg's model is the following nonvanishing result.
Theorem 2.31 The classes ![]() $\nu ^*(e^k)\in H^{2k}(\mathrm {B}\Gamma _2^{\mathrm {PL}};\mathbb {Q})$ are nontrivial for all
$\nu ^*(e^k)\in H^{2k}(\mathrm {B}\Gamma _2^{\mathrm {PL}};\mathbb {Q})$ are nontrivial for all ![]() $k$.
$k$.
This is in contrast to the smooth case. Since in the smooth case we also have the Euler class ![]() $\nu ^*(e)\in H^2(\mathrm {B}\Gamma _2;\mathbb {Q})$ and as a consequence of the Bott vanishing theorem
$\nu ^*(e)\in H^2(\mathrm {B}\Gamma _2;\mathbb {Q})$ and as a consequence of the Bott vanishing theorem ![]() $\nu ^*(e^4)$ vanishes in
$\nu ^*(e^4)$ vanishes in ![]() $H^8(\mathrm {B}\Gamma _2;\mathbb {Q})$. However, as we will see in the PL case, all the powers
$H^8(\mathrm {B}\Gamma _2;\mathbb {Q})$. However, as we will see in the PL case, all the powers ![]() $\nu^* (e^k)$ are nontrivial. Instead of the identity component, if we consider the entire group
$\nu^* (e^k)$ are nontrivial. Instead of the identity component, if we consider the entire group ![]() ${\mathrm {PL}}^{\delta }(\Sigma,\mathrm {rel}\,\partial )$, using Theorem 2.31 and the method in [Reference NarimanNar17, Theorem 0.4], we can prove the following nonvanishing result in the stable range.
${\mathrm {PL}}^{\delta }(\Sigma,\mathrm {rel}\,\partial )$, using Theorem 2.31 and the method in [Reference NarimanNar17, Theorem 0.4], we can prove the following nonvanishing result in the stable range.
Theorem 2.32 Let ![]() $\Sigma$ be a compact orientable surface. Then the map
$\Sigma$ be a compact orientable surface. Then the map
induces an injection when ![]() $*\leq (2g(\Sigma )-2)/3$ where
$*\leq (2g(\Sigma )-2)/3$ where ![]() $g(\Sigma )$ is the genus of the surface
$g(\Sigma )$ is the genus of the surface ![]() $\Sigma$.
$\Sigma$.
As a consequence of the Madsen–Weiss theorem [Reference Madsen and WeissMW07], ![]() $H^*(\mathrm {B}{\mathrm {PL}}(\Sigma,\mathrm {rel}\,\partial );\mathbb {Q})$ is isomorphic to the polynomial ring
$H^*(\mathrm {B}{\mathrm {PL}}(\Sigma,\mathrm {rel}\,\partial );\mathbb {Q})$ is isomorphic to the polynomial ring ![]() $\mathbb {Q}[\kappa _1,\kappa _2,\dots ]$ in the stable range,
$\mathbb {Q}[\kappa _1,\kappa _2,\dots ]$ in the stable range, ![]() $*\leq (2g(\Sigma )-2)/3$. Here the
$*\leq (2g(\Sigma )-2)/3$. Here the ![]() $\kappa _i$ are certain characteristic classes of surface bundles known as
$\kappa _i$ are certain characteristic classes of surface bundles known as ![]() $i$th MMM classes whose degree is
$i$th MMM classes whose degree is ![]() $2i$. This is also in contrast to the case of smooth diffeomorphisms. In particular, we have the following nonvanishing result.
$2i$. This is also in contrast to the case of smooth diffeomorphisms. In particular, we have the following nonvanishing result.
Corollary 2.16 The ![]() $\kappa _i$ are all nontrivial in
$\kappa _i$ are all nontrivial in ![]() $H^*(\mathrm {B}{\mathrm {PL}}^{\delta }(\Sigma,\mathrm {rel}\,\partial );\mathbb {Q})$ as long as
$H^*(\mathrm {B}{\mathrm {PL}}^{\delta }(\Sigma,\mathrm {rel}\,\partial );\mathbb {Q})$ as long as ![]() $i\leq (2g(\Sigma )-2)/6$.
$i\leq (2g(\Sigma )-2)/6$.
Since the proof of Theorem 2.32 uses some background from [Reference NarimanNar17, §§ 1 and 2], we shall first explain how to adapt these techniques to the case of PL homeomorphisms of surfaces. The proofs in [Reference NarimanNar17] are formulated for diffeomorphism groups of surfaces, but since, in dimension ![]() $2$, the diffeomorphism group of a surface has the same homotopy type as the PL homeomorphism group, we can use the results of [Reference NarimanNar17] as follows.
$2$, the diffeomorphism group of a surface has the same homotopy type as the PL homeomorphism group, we can use the results of [Reference NarimanNar17] as follows.
In dimension ![]() $2$, we know [Reference Balcerak and HajdukBH81, p. 8] that
$2$, we know [Reference Balcerak and HajdukBH81, p. 8] that ![]() $\phi \colon \mathrm {B}\mathrm {GL}^+_2(\mathbb {R})\to \mathrm {B}\mathrm {PL}^+_2(\mathbb {R})$ and
$\phi \colon \mathrm {B}\mathrm {GL}^+_2(\mathbb {R})\to \mathrm {B}\mathrm {PL}^+_2(\mathbb {R})$ and ![]() $\eta \colon \mathrm {B}\mathrm {PL}^+_2(\mathbb {R})\to \mathrm {B}\mathrm {Top}^+_2$ are weak homotopy equivalences where
$\eta \colon \mathrm {B}\mathrm {PL}^+_2(\mathbb {R})\to \mathrm {B}\mathrm {Top}^+_2$ are weak homotopy equivalences where ![]() $\mathrm {Top}^+_2$ is the group of orientation-preserving homeomorphisms of
$\mathrm {Top}^+_2$ is the group of orientation-preserving homeomorphisms of ![]() $\mathbb {R}^2$. Let
$\mathbb {R}^2$. Let ![]() $\rho$ be a homotopy inverse to
$\rho$ be a homotopy inverse to ![]() $\eta$. We shall consider the tangential structures
$\eta$. We shall consider the tangential structures
where ![]() $\phi ^*(\nu )$ and
$\phi ^*(\nu )$ and ![]() $\rho ^*(\nu )$ are the pullbacks of the fibration induced by
$\rho ^*(\nu )$ are the pullbacks of the fibration induced by ![]() $\nu$ with the homotopy fiber
$\nu$ with the homotopy fiber ![]() $\overline {\mathrm {B}\Gamma }_2^{\mathrm {PL}}$. Hence, these fibrations are all fiber homotopy equivalent. Let
$\overline {\mathrm {B}\Gamma }_2^{\mathrm {PL}}$. Hence, these fibrations are all fiber homotopy equivalent. Let ![]() $\tau ^s_{\Sigma }, \tau ^p_{\Sigma }$ and
$\tau ^s_{\Sigma }, \tau ^p_{\Sigma }$ and ![]() $\tau ^t_{\Sigma }$ be the map classifying the tangent (micro)bundles in the smooth, PL and topological category. respectively.
$\tau ^t_{\Sigma }$ be the map classifying the tangent (micro)bundles in the smooth, PL and topological category. respectively.
Given the above homotopy equivalences, the space of sections ![]() $\mathrm {Sect}_{\partial }((\tau ^s_{\Sigma })^*(\nu ^s))$,
$\mathrm {Sect}_{\partial }((\tau ^s_{\Sigma })^*(\nu ^s))$, ![]() $\mathrm {Sect}_{\partial }((\tau ^p_{\Sigma })^*(\nu ))$ and
$\mathrm {Sect}_{\partial }((\tau ^p_{\Sigma })^*(\nu ))$ and ![]() $\mathrm {Sect}_{\partial }((\tau ^t_{\Sigma })^*(\nu ^t))$ are also all homotopy equivalent. Now since we have
$\mathrm {Sect}_{\partial }((\tau ^t_{\Sigma })^*(\nu ^t))$ are also all homotopy equivalent. Now since we have ![]() $\mathrm {Diff}(\Sigma, \mathrm {rel}\,\partial )\simeq \mathrm {Homeo}(\Sigma, \mathrm {rel}\,\partial )\simeq \mathrm {PL}(\Sigma, \mathrm {rel}\,\partial )$ [Reference Balcerak and HajdukBH81, p. 8], we get a zigzag of weak homotopy equivalences
$\mathrm {Diff}(\Sigma, \mathrm {rel}\,\partial )\simeq \mathrm {Homeo}(\Sigma, \mathrm {rel}\,\partial )\simeq \mathrm {PL}(\Sigma, \mathrm {rel}\,\partial )$ [Reference Balcerak and HajdukBH81, p. 8], we get a zigzag of weak homotopy equivalences

But as we explained, the analog of the Mather–Thurston theorem for PL homeomorphisms, the equivariance of the homology equivalence (2.28) implies that
is homology isomorphic to ![]() $\mathrm {B}{\mathrm {PL}}^{\delta }(\Sigma,\mathrm {rel}\,\partial )$. Given the above zigzag, we have the following lemma.
$\mathrm {B}{\mathrm {PL}}^{\delta }(\Sigma,\mathrm {rel}\,\partial )$. Given the above zigzag, we have the following lemma.
Lemma 2.34 The classifying space ![]() $\mathrm {B}{\mathrm {PL}}^{\delta }(\Sigma,\mathrm {rel}\,\partial )$ is homology isomorphic to
$\mathrm {B}{\mathrm {PL}}^{\delta }(\Sigma,\mathrm {rel}\,\partial )$ is homology isomorphic to ![]() $|S_{\bullet }({\rm Sect}_c((\tau ^s_{\Sigma })^*|$
$|S_{\bullet }({\rm Sect}_c((\tau ^s_{\Sigma })^*|$ ![]() $(\nu ^s)))|/\!\!/ |S_{\bullet }({\rm Diff}(\Sigma, \mathrm {rel}\,\partial ))|$.
$(\nu ^s)))|/\!\!/ |S_{\bullet }({\rm Diff}(\Sigma, \mathrm {rel}\,\partial ))|$.
On the other hand, there is a natural map [Reference NarimanNar17, (1.12)] from
to the moduli space ![]() $\mathcal {M}^{\nu ^s}(\Sigma )$ of tangential
$\mathcal {M}^{\nu ^s}(\Sigma )$ of tangential ![]() $\nu ^s$-structures on
$\nu ^s$-structures on ![]() $\Sigma$ defined in [Reference NarimanNar17, § 1.2.3]. The space
$\Sigma$ defined in [Reference NarimanNar17, § 1.2.3]. The space ![]() $\mathcal {M}^{\nu ^s}(\Sigma )$ has been very well studied, and we used the techniques of [Reference Randal-WilliamsRW16, Reference Galatius, Madsen, Tillmann and WeissGMTW09, Reference Galatius and Randal-WilliamsGRW10] in [Reference NarimanNar17] to show that it exhibits homological stability. As we shall recall in the following proof, its stable homology is described in terms of the Madsen–Tillman spectrum of the corresponding tangential structure.
$\mathcal {M}^{\nu ^s}(\Sigma )$ has been very well studied, and we used the techniques of [Reference Randal-WilliamsRW16, Reference Galatius, Madsen, Tillmann and WeissGMTW09, Reference Galatius and Randal-WilliamsGRW10] in [Reference NarimanNar17] to show that it exhibits homological stability. As we shall recall in the following proof, its stable homology is described in terms of the Madsen–Tillman spectrum of the corresponding tangential structure.
Proof Proof of Theorems 2.31 and 2.32
The key point in Lemma 2.20 is that Greenberg's model for ![]() $\mathrm {B}\Gamma _2^{\mathrm {PL}}$ allows us, up to homotopy, to find a section for the map
$\mathrm {B}\Gamma _2^{\mathrm {PL}}$ allows us, up to homotopy, to find a section for the map
Recall that a null-homotopic map ![]() $X\to \mathrm {B}S^1$ and the natural map
$X\to \mathrm {B}S^1$ and the natural map ![]() $LX/\!\!/ S^1\to \mathrm {B}S^1$ induce a map
$LX/\!\!/ S^1\to \mathrm {B}S^1$ induce a map ![]() $rX\to \mathrm {B}S^1$. But a section to the map
$rX\to \mathrm {B}S^1$. But a section to the map ![]() $LX/\!\!/ S^1\to \mathrm {B}S^1$ induces a section for
$LX/\!\!/ S^1\to \mathrm {B}S^1$ induces a section for ![]() $rX\to \mathrm {B}S^1$. Therefore,
$rX\to \mathrm {B}S^1$. Therefore, ![]() $\nu ^*(e^k)\in H^{2k}( \mathrm {B}\Gamma _2^{\mathrm {PL}};\mathbb {Q})$ are nontrivial for all
$\nu ^*(e^k)\in H^{2k}( \mathrm {B}\Gamma _2^{\mathrm {PL}};\mathbb {Q})$ are nontrivial for all ![]() $k$.
$k$.
Now let ![]() $\gamma$ be the tautological
$\gamma$ be the tautological ![]() $2$-plane bundle over
$2$-plane bundle over ![]() $\mathrm {B}S^1$ and let
$\mathrm {B}S^1$ and let ![]() $\mathrm {MT}\nu ^s$ be the Thom spectrum of the virtual bundle
$\mathrm {MT}\nu ^s$ be the Thom spectrum of the virtual bundle ![]() $(\nu ^s)^*(-\gamma )$. And let
$(\nu ^s)^*(-\gamma )$. And let ![]() $\Omega ^{\infty }_0 \mathrm {MT}\nu ^s$ be the base point component of the infinite loop space associated with this Thom spectrum. Then exactly the same method as in [Reference NarimanNar17, Theorem 0.4] goes through to show that there is a map
$\Omega ^{\infty }_0 \mathrm {MT}\nu ^s$ be the base point component of the infinite loop space associated with this Thom spectrum. Then exactly the same method as in [Reference NarimanNar17, Theorem 0.4] goes through to show that there is a map
which is homology isomorphism up to degrees ![]() $*\leq (2g(\Sigma )-2)/3$. Hence, we obtain
$*\leq (2g(\Sigma )-2)/3$. Hence, we obtain
in degrees ![]() $*\leq (2g(\Sigma )-2)/3$ where the right-hand side is the polynomial ring with the generators in the graded vector space
$*\leq (2g(\Sigma )-2)/3$ where the right-hand side is the polynomial ring with the generators in the graded vector space ![]() $H^{*>2}(\mathrm {B}\Gamma _2^{\mathrm {PL}};\mathbb {Q})$ which is shifted by degree
$H^{*>2}(\mathrm {B}\Gamma _2^{\mathrm {PL}};\mathbb {Q})$ which is shifted by degree ![]() $2$. Since by the Madsen–Weiss theorem
$2$. Since by the Madsen–Weiss theorem ![]() $H^*(\mathrm {B}\mathrm {PL}(\Sigma,\mathrm {rel}\,\partial );\mathbb {Q})$ is isomorphic to
$H^*(\mathrm {B}\mathrm {PL}(\Sigma,\mathrm {rel}\,\partial );\mathbb {Q})$ is isomorphic to ![]() $\mathrm {Sym}^*(H^{*>2}(\mathrm {B}S^1;\mathbb {Q})[-2])$ in the same stable range and we know that
$\mathrm {Sym}^*(H^{*>2}(\mathrm {B}S^1;\mathbb {Q})[-2])$ in the same stable range and we know that
is injective, then so is
in stable range.
Acknowledgements
The author would like to thank Gael Meigniez for the discussion about the Haefliger–Thurston conjecture and Alexander Kupers for bringing up Suslin's calculations in [Reference SuslinSus91] and his comments on the proof of Theorem 2.4. The author also thanks the referees for very helpful comments and suggestions to improve the readability – in particular, one of them suggested Lemma 2.9.
Conflicts of interest
None.
Financial support
The author was partially supported by NSF DMS-2113828, NSF CAREER Grant DMS-2239106 and Simons Foundation (855209, SN).
Journal information
Compositio Mathematica is owned by the Foundation Compositio Mathematica and published by the London Mathematical Society in partnership with Cambridge University Press. All surplus income from the publication of Compositio Mathematica is returned to mathematics and higher education through the charitable activities of the Foundation, the London Mathematical Society and Cambridge University Press.