Sheaves of categories with local actions of Hochschild cochains

Abstract

The notion of Hochschild cochains induces an assignment from 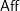$\mathsf{Aff}$, affine DG schemes, to monoidal DG categories. We show that this assignment extends, under appropriate finiteness conditions, to a functor 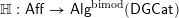$\mathbb{H}:\mathsf{Aff}\rightarrow \mathsf{Alg}^{\text{bimod}}(\mathsf{DGCat})$, where the latter denotes the category of monoidal DG categories and bimodules. Any functor 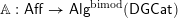$\mathbb{A}:\mathsf{Aff}\rightarrow \mathsf{Alg}^{\text{bimod}}(\mathsf{DGCat})$ gives rise, by taking modules, to a theory of sheaves of categories 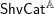$\mathsf{ShvCat}^{\mathbb{A}}$. In this paper, we study 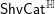$\mathsf{ShvCat}^{\mathbb{H}}$. Loosely speaking, this theory categorifies the theory of 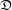$\mathfrak{D}$-modules, in the same way as Gaitsgory’s original 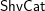$\mathsf{ShvCat}$ categorifies the theory of quasi-coherent sheaves. We develop the functoriality of 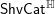$\mathsf{ShvCat}^{\mathbb{H}}$, its descent properties and the notion of 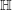$\mathbb{H}$-affineness. We then prove the 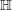$\mathbb{H}$-affineness of algebraic stacks: for 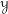${\mathcal{Y}}$ a stack satisfying some mild conditions, the 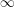$\infty$-category 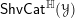$\mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Y}})$ is equivalent to the 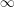$\infty$-category of modules for 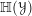$\mathbb{H}({\mathcal{Y}})$, the monoidal DG category of higher differential operators. The main consequence, for 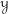${\mathcal{Y}}$ quasi-smooth, is the following: if 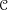${\mathcal{C}}$ is a DG category acted on by 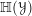$\mathbb{H}({\mathcal{Y}})$, then 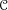${\mathcal{C}}$ admits a theory of singular support in 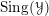$\operatorname{Sing}({\mathcal{Y}})$, where 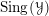$\operatorname{Sing}({\mathcal{Y}})$ is the space of singularities of 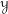${\mathcal{Y}}$. As an application to the geometric Langlands programme, we indicate how derived Satake yields an action of 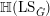$\mathbb{H}(\operatorname{LS}_{{\check{G}}})$ on 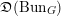$\mathfrak{D}(\operatorname{Bun}_{G})$, thereby equipping objects of 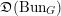$\mathfrak{D}(\operatorname{Bun}_{G})$ with singular support in 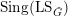$\operatorname{Sing}(\operatorname{LS}_{{\check{G}}})$.