Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T08:32:21.431Z Has data issue: false hasContentIssue false
  • English
  • Français

ASYMPTOTIC THEORY FOR EMPIRICAL SIMILARITY MODELS

Published online by Cambridge University Press:  04 November 2009

Offer Lieberman
Offer Lieberman*
Affiliation:
University of Haifa
*
*Address correspondence to Offer Lieberman, Department of Economics, University of Haifa, Haifa 31905, Israel; e-mail: offerl@econ.haifa.ac.il.
Get access Rights & Permissions [Opens in a new window]

Abstract

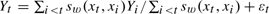We consider the stochastic process , t = 2, …, n, where sw(xt, xi) is a similarity function between the tth and the ith observations and {εt} is a random disturbance term. This process was originally axiomatized by Gilboa, Lieberman, and Schmeidler (2006, Review of Economics and Statistics 88, 433–444) as a way by which agents, or even nature, reason. In the present paper, consistency and the asymptotic distribution of the quasi-maximum likelihood estimator of the parameters of the model are established. Connections to other models and techniques are drawn. In its general form, the model does not fall within any class of nonstationary econometric models for which asymptotic theory is available. For this reason, the developments in this paper are new and nonstandard.

Type
ARTICLES
Information
Econometric Theory , Volume 26 , Issue 4 , August 2010 , pp. 1032 - 1059
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Andrews, D.W.K. (1999) Estimation when a parameter is on a boundary. Econometrica 67, 1341–1383.CrossRefGoogle Scholar
Basawa, I.V. & Scott, D.J. (1983) Asymptotic Optimal Inference for Non-Ergodic Models. Springer-Verlag.CrossRefGoogle Scholar
Comte, F. & Lieberman, O. (2003) Asymptotic theory for multivariate GARCH processes. Journal of Multivariate Analysis 84, 61–84.CrossRefGoogle Scholar
Feigin, P.D. (1976) Maximum likelihood estimation for continuous time stochastic processes. Advances in Applied Probability 8, 712–736.CrossRefGoogle Scholar
Fernandes, M., Medeiros, M., & Scharth, M. (2007) Modeling and Predicting the CBOE Market Volatility Index. Textos para discussao no. 548, Department of Economics, PUC-Rio, Brazil.Google Scholar
Gallant, A.R. (1987) Nonlinear Statistical Models. Wiley.CrossRefGoogle Scholar
Gallant, A.R. & White, H. (1988) A Unified Theory of Estimation and Inference for Nonlinear Dynamic Models. Basil Blackwell.Google Scholar
Gayer, G., Gilboa, I. & Lieberman, O. (2007) Rule-based and case-based reasoning in housing prices. B.E. Journal in Theoretical Economics 7(1) (Advances), Article 10.CrossRefGoogle Scholar
Gilboa, I., Lieberman, O., & Schmeidler, D. (2006) Empirical similarity. Review of Economics and Statistics 88, 433–444.CrossRefGoogle Scholar
Gilboa, I., Lieberman, O., & Schmeidler, D. (2010) A similarity-based approach to prediction. Journal of Econometrics, forthcoming.Google Scholar
Hayashi, F. (2000) Econometrics. Princeton University Press.Google Scholar
Heyde, C.C. (1975) Remarks in efficiency of estimation for branching processes. Biometrika 62, 49–55.CrossRefGoogle Scholar
Horn, R.A. & Johnson, C.R. (1985) Matrix Analysis. Cambridge University Press.CrossRefGoogle Scholar
Jeganathan, P. (1982) On the asymptotic theory of estimation when the limit of the log-likelihood ratios is mixed normal. Sankhya A 44, 173–212.Google Scholar
Kelejian, H.H. & Prucha, I.R. (1998) A generalized spatial two-stage least squares procedure for estimating a spatial autoregressive model with autoregressive disturbances. Journal of Real Estate Finance and Economics 17, 99–121.CrossRefGoogle Scholar
Lee, L.F. (2004) Asymptotic distributions of quasi-maximum likelihood estimators for spatial autoregressive models. Econometrica 72, 1899–1925.CrossRefGoogle Scholar
Lieberman, O. (1997) The effect of nonnormality. Econometric Theory 13, 52–78.CrossRefGoogle Scholar
Magnus, J.R. & Neudecker, H. (1988) Matrix Differential Calculus with Applications in Statistics and Econometrics. Wiley.Google Scholar
Phillips, P.C.B. (1987) Time series regression with a unit root. Econometrica 55, 277–301.CrossRefGoogle Scholar
Pötscher, B.M. & Prucha, I.R. (1997) Dynamic Nonlinear Statistical Models: Asymptotic Theory. Springer-Verlag.Google Scholar
Saikkonen, P. (1995) Problems with the asymptotic theory of maximum likelihood estimation in integrated and cointegrated systems. Econometric Theory 11, 888–911.CrossRefGoogle Scholar
Varberg, D.E. (1966) Convergence of quadratic forms in independent random variables. Annals of Mathematical Statistics 37, 567–576.CrossRefGoogle Scholar
White, H. (1994) Estimation, Inference and Specification Analysis. Cambridge University Press.CrossRefGoogle Scholar
Wu, C.F. (1981) Asymptotic theory of nonlinear least squares estimation. Annals of Statistics 9, 501–513.CrossRefGoogle Scholar