Refine listing
Actions for selected content:
Contents
ARTICLES
ESTIMATION FOR A NONSTATIONARY SEMI-STRONG GARCH(1,1) MODEL WITH HEAVY-TAILED ERRORS
-
- Published online by Cambridge University Press:
- 19 June 2009, pp. 1-28
-
- Article
- Export citation
Research Article
INSTRUMENTAL VARIABLE ESTIMATION IN A DATARICH ENVIRONMENT
-
- Published online by Cambridge University Press:
- 17 March 2010, pp. 1577-1606
-
- Article
- Export citation
A SIEVE BOOTSTRAP TEST FOR COINTEGRATION INA CONDITIONAL ERROR CORRECTION MODEL
-
- Published online by Cambridge University Press:
- 26 October 2009, pp. 647-681
-
- Article
- Export citation
ARTICLES
ASYMPTOTICALLY UNBIASED ESTIMATION OF AUTOCOVARIANCES AND AUTOCORRELATIONS WITH LONG PANEL DATA
-
- Published online by Cambridge University Press:
- 17 February 2010, pp. 1263-1304
-
- Article
- Export citation
Obituary
Arthur S. Goldberger,1930–2009
-
- Published online by Cambridge University Press:
- 04 March 2010, pp. 327-329
-
- Article
-
- You have access
- Export citation
ARTICLES
SUP-TESTS FOR LINEARITY IN A GENERAL NONLINEAR AR(1) MODEL
-
- Published online by Cambridge University Press:
- 04 November 2009, pp. 965-993
-
- Article
- Export citation
SPLINE-BACKFITTED KERNEL SMOOTHING OF ADDITIVE COEFFICIENT MODEL
-
- Published online by Cambridge University Press:
- 12 January 2010, pp. 29-59
-
- Article
- Export citation
Research Article
INFERENCE FOR THE JUMP PART OF QUADRATICVARIATION OF ITÔ SEMIMARTINGALES
-
- Published online by Cambridge University Press:
- 18 August 2009, pp. 331-368
-
- Article
- Export citation
TESTS FOR NONLINEARCOINTEGRATION
-
- Published online by Cambridge University Press:
- 07 October 2009, pp. 682-709
-
- Article
- Export citation
ARTICLES
UNIT ROOT TESTS WITH WAVELETS
-
- Published online by Cambridge University Press:
- 17 February 2010, pp. 1305-1331
-
- Article
- Export citation
Research Article
SMOOTH VARYING-COEFFICIENT ESTIMATION ANDINFERENCE FOR QUALITATIVE AND QUANTITATIVEDATA
-
- Published online by Cambridge University Press:
- 17 March 2010, pp. 1607-1637
-
- Article
- Export citation
ARTICLES
IMPROVED AND EXTENDED END-OF-SAMPLE INSTABILITY TESTS USING A FEASIBLE QUASI-GENERALIZED LEAST SQUARES PROCEDURE
-
- Published online by Cambridge University Press:
- 04 November 2009, pp. 994-1031
-
- Article
- Export citation
Research Article
LOCAL IDENTIFICATION IN EMPIRICAL GAMES OFINCOMPLETE INFORMATION
-
- Published online by Cambridge University Press:
- 17 March 2010, pp. 1638-1662
-
- Article
- Export citation
ARTICLES
NONPARAMETRIC FILTERING OF THE REALIZED SPOT VOLATILITY: A KERNEL-BASED APPROACH
-
- Published online by Cambridge University Press:
- 19 June 2009, pp. 60-93
-
- Article
- Export citation
Research Article
A TWO-STAGE PLUG-IN BANDWIDTH SELECTION ANDITS IMPLEMENTATION FOR COVARIANCEESTIMATION
-
- Published online by Cambridge University Press:
- 26 October 2009, pp. 710-743
-
- Article
- Export citation
ARTICLES
ESTIMATION OF UNIT ROOT SPATIAL DYNAMIC PANEL DATA MODELS
-
- Published online by Cambridge University Press:
- 17 February 2010, pp. 1332-1362
-
- Article
- Export citation
ASYMPTOTIC THEORY FOR EMPIRICAL SIMILARITY MODELS
-
- Published online by Cambridge University Press:
- 04 November 2009, pp. 1032-1059
-
- Article
- Export citation
Research Article
THE IMPACT OF A HAUSMAN PRETEST ON THEASYMPTOTIC SIZE OF A HYPOTHESIS TEST
-
- Published online by Cambridge University Press:
- 18 August 2009, pp. 369-382
-
- Article
- Export citation
M-ESTIMATION FOR A SPATIALUNILATERAL AUTOREGRESSIVE MODEL WITH INFINITEVARIANCE INNOVATIONS
-
- Published online by Cambridge University Press:
- 17 March 2010, pp. 1663-1682
-
- Article
- Export citation
ARTICLES
TESTS OF THE MARTINGALE DIFFERENCE HYPOTHESIS USING BOOSTING AND RBF NEURAL NETWORK APPROXIMATIONS
-
- Published online by Cambridge University Press:
- 17 February 2010, pp. 1363-1397
-
- Article
- Export citation
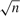 to a normal distribution under very mild moment conditions for the errors. Furthermore, when the distributions of the errors are in the domain of attraction of a stable law with the exponent
to a normal distribution under very mild moment conditions for the errors. Furthermore, when the distributions of the errors are in the domain of attraction of a stable law with the exponent 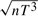 consistent and the estimates of other parameters are
consistent and the estimates of other parameters are 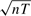 consistent, and all of them are asymptotically normal. For the latter model the sum of the contemporaneous spatial effect and dynamic spatial effect converges at
consistent, and all of them are asymptotically normal. For the latter model the sum of the contemporaneous spatial effect and dynamic spatial effect converges at 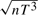 rate. We also propose a bias-correction procedure so that the asymptotic biases of those estimates are eliminated as long as
rate. We also propose a bias-correction procedure so that the asymptotic biases of those estimates are eliminated as long as 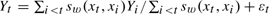 ,
,