Article contents
JIVE FOR PANEL DYNAMIC SIMULTANEOUS EQUATIONS MODELS
Published online by Cambridge University Press: 02 November 2017
Abstract
We consider the method of moments estimation of a structural equation in a panel dynamic simultaneous equations model under different sample size combinations of cross-sectional dimension, N, and time series dimension, T. Two types of linear transformation to remove the individual-specific effects from the model, first difference and forward orthogonal demeaning, are considered. We show that the Alvarez and Arellano (2003) type GMM estimator under both transformations is consistent only if 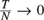 ${T \over N} \to 0$ as
${T \over N} \to 0$ as 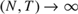 $\left( {N,T} \right) \to \infty $. However, it is asymptotically biased if
$\left( {N,T} \right) \to \infty $. However, it is asymptotically biased if 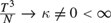 ${{{T^3}} \over N} \to \kappa \ne 0 < \infty$ as
${{{T^3}} \over N} \to \kappa \ne 0 < \infty$ as 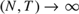 $\left( {N,T} \right) \to \infty $. Since the validity of statistical inference depends critically on whether an estimator is asymptotically unbiased, we suggest a jackknife bias reduction method and derive its limiting distribution. Monte Carlo studies are conducted to demonstrate the importance of using an asymptotically unbiased estimator to obtain valid statistical inference.
$\left( {N,T} \right) \to \infty $. Since the validity of statistical inference depends critically on whether an estimator is asymptotically unbiased, we suggest a jackknife bias reduction method and derive its limiting distribution. Monte Carlo studies are conducted to demonstrate the importance of using an asymptotically unbiased estimator to obtain valid statistical inference.
Information
- Type
- ARTICLES
- Information
- Copyright
- Copyright © Cambridge University Press 2017
Footnotes
We would like to thank the editor, Peter C.B. Phillips, the co-editor, Guido Kuersteiner, John Chao and three anonymous referees for very detailed and helpful comments and suggestions, which have greatly improved the original paper. We would also like to thank Alan Adelman and John Pedersen for editorial polishing. All remaining errors are solely ours. Partial research support of China NSF grant #71131008 and #71631004 to the first author is gratefully acknowledged.
References
REFERENCES
- 3
- Cited by

