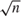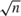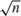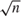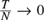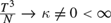Contents
ARTICLES
STATIONARY INTEGRATED ARCH(∞) AND AR(∞) PROCESSES WITH FINITE VARIANCE
-
- Published online by Cambridge University Press:
- 17 October 2017, pp. 1159-1179
-
- Article
- Export citation
ROOT-N CONSISTENCY OF INTERCEPT ESTIMATORS IN A BINARY RESPONSE MODEL UNDER TAIL RESTRICTIONS
-
- Published online by Cambridge University Press:
- 02 November 2017, pp. 1180-1206
-
- Article
- Export citation
NONPARAMETRIC STOCHASTIC VOLATILITY
-
- Published online by Cambridge University Press:
- 03 July 2018, pp. 1207-1255
-
- Article
- Export citation
NONPARAMETRIC INSTRUMENTAL REGRESSION WITH ERRORS IN VARIABLES
-
- Published online by Cambridge University Press:
- 14 February 2018, pp. 1256-1280
-
- Article
- Export citation
NONPARAMETRIC TWO-STEP SIEVE M ESTIMATION AND INFERENCE
-
- Published online by Cambridge University Press:
- 25 April 2018, pp. 1281-1324
-
- Article
- Export citation
JIVE FOR PANEL DYNAMIC SIMULTANEOUS EQUATIONS MODELS
-
- Published online by Cambridge University Press:
- 02 November 2017, pp. 1325-1369
-
- Article
- Export citation
MISCELLANEA
RENORMING VOLATILITIES IN A FAMILY OF GARCH MODELS
-
- Published online by Cambridge University Press:
- 11 December 2017, pp. 1370-1382
-
- Article
- Export citation
BLOCK BOOTSTRAP CONSISTENCY UNDER WEAK ASSUMPTIONS
-
- Published online by Cambridge University Press:
- 01 February 2018, pp. 1383-1406
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ECT volume 34 issue 6 Cover and Front matter
-
- Published online by Cambridge University Press:
- 08 November 2018, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
ECT volume 34 issue 6 Cover and Back matter
-
- Published online by Cambridge University Press:
- 08 November 2018, pp. b1-b6
-
- Article
-
- You have access
- Export citation