Article contents
ROOT-N CONSISTENCY OF INTERCEPT ESTIMATORS IN A BINARY RESPONSE MODEL UNDER TAIL RESTRICTIONS
Published online by Cambridge University Press: 02 November 2017
Abstract
The intercept of the binary response model is not regularly identified (i.e., 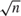 $\sqrt n$ consistently estimable) when the support of both the special regressor V and the error term ε are the whole real line. The estimator of the intercept potentially has a slower than
$\sqrt n$ consistently estimable) when the support of both the special regressor V and the error term ε are the whole real line. The estimator of the intercept potentially has a slower than 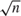 $\sqrt n$ convergence rate, which can result in a large estimation error in practice. This paper imposes additional tail restrictions which guarantee the regular identification of the intercept and thus the
$\sqrt n$ convergence rate, which can result in a large estimation error in practice. This paper imposes additional tail restrictions which guarantee the regular identification of the intercept and thus the 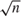 $\sqrt n$-consistency of its estimator. We then propose an estimator that achieves the
$\sqrt n$-consistency of its estimator. We then propose an estimator that achieves the 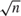 $\sqrt n$ rate. Last, we extend our tail restrictions to a full-blown model with endogenous regressors.
$\sqrt n$ rate. Last, we extend our tail restrictions to a full-blown model with endogenous regressors.
Information
- Type
- ARTICLES
- Information
- Copyright
- Copyright © Cambridge University Press 2017
Footnotes
We thank Shakeeb Khan, Federico Bugni, Arnaud Maurel, Xavier D’Haultfœuille, the editor, the co-editor, three anonymous referees, and the participants in the 2014 Econometric Society China Summer Meeting and the Duke microeconometrics lunch group for their comments. The first author acknowledges financial support from Project 71563062 supported by National Natural Science Foundation of China and Key Project of the National Social Science Foundation of China (Grant No. 13AZD082). The usual disclaimer applies.
References
REFERENCES
- 1
- Cited by

