Contents
Articles
Testing a Parametric Model Against a Semiparametric Alternative
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 821-848
-
- Article
- Export citation
Testing for Second-Order Stochastic Dominance of Two Distributions
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 849-866
-
- Article
- Export citation
On the Asymptotic Optimality of Alternative Minimum-Distance Estimators in Linear Latent-Variable Models
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 867-883
-
- Article
- Export citation
A Note on Autoregressive Modeling
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 884-899
-
- Article
- Export citation
On the Approximation of Saddlepoint Expansions in Statistics
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 900-916
-
- Article
- Export citation
Testing for Unit Roots in Models with Structural Change
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 917-936
-
- Article
- Export citation
Asymptotic Distributions of the Least-Squares Estimators and Test Statistics in the Near Unit Root Model with Non-Zero Initial Value and Local Drift and Trend
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 937-966
-
- Article
- Export citation
Problems
Fully Modified Least Squares in I(2) Regression
-
- Published online by Cambridge University Press:
- 11 February 2009, p. 967
-
- Article
- Export citation
Spurious Regression and Generalized Least Squares
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 967-968
-
- Article
- Export citation
The Asymptotic Power of RESET for Detecting Omitted Variables
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 968-969
-
- Article
- Export citation
A Strong Law of Large Numbers
-
- Published online by Cambridge University Press:
- 11 February 2009, p. 969
-
- Article
- Export citation
Announcement
The Zellner Thesis Award in Business and Economic Statistics
-
- Published online by Cambridge University Press:
- 11 February 2009, p. 970
-
- Article
- Export citation
Index
Cumulative Index To Volume 10, 1994
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 971-976
-
- Article
- Export citation
Back matter
ECT volume 10 issue 5 Cover and Back matter
-
- Published online by Cambridge University Press:
- 11 February 2009, p. f1
-
- Article
-
- You have access
- Export citation
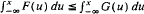 , for all
, for all 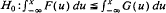 , for some
, for some 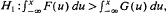 , for all
, for all