For the problem of testing the hypothesis that all m coefficients of the right-hand-side endogenous variables in an instrumental variables (IV) regression are zero, the likelihood ratio (LR) test can, if the reduced form covariance matrix is known, be rendered similar by a conditioning argument. To exploit this fact requires knowledge of the relevant conditional cumulative distribution function (c.d.f.) of the LR statistic, but the statistic is a function of the smallest characteristic root of an (m + 1)-square matrix and is therefore analytically difficult to deal with when m > 1. We show in this paper that an iterative conditioning argument used by Hillier (2009) and Andrews, Moreira, and Stock (2007 Journal of Econometrics 139, 116–132) to evaluate the c.d.f. in the case m = 1 can be generalized to the case of arbitrary m. This means that we can completely bypass the difficulty of dealing with the smallest characteristic root. Analytic results are obtained for the case m = 2, and a simple and efficient simulation approach to evaluating the c.d.f. is suggested for larger values of m.

This paper investigates the asymptotic theory for a factor GARCH (generalized autoregressive conditional heteroskedasticity) model. Sufficient conditions for asymptotic stability and existence of moments are established. These conditions allow for volatility spillover and integrated GARCH. We then show the strong consistency and asymptotic normality of the quasi–maximum likelihood estimator (QMLE) of the model parameters. The results are obtained under the finiteness of the fourth-order moment of the innovations.

This paper develops a framework for the construction and analysis of parametric misspecification tests for generalized autoregressive conditional heteroskedastic (GARCH) models, based on first-order asymptotic theory. The principal finding is that estimation effects from the correct specification of the conditional mean (regression) function can be asymptotically nonnegligible. This implies that certain procedures, such as the asymmetry tests of Engle and Ng (1993, Journal of Finance 48, 1749–1777) and the nonlinearity test of Lundbergh and Teräsvirta (2002, Journal of Econometrics 110, 417–435), are asymptotically invalid. A second contribution is the proposed use of alternative tests for asymmetry and/or nonlinearity that, it is conjectured, should enjoy improved power properties. A Monte Carlo study supports the principal theoretical findings and also suggests that the new tests have fairly good size and very good power properties when compared with the Engle and Ng (1993) and Lundbergh and Teräsvirta (2002) procedures.

We study test procedures that detect structural breaks in underlying data sequences. In particular, we wish to discriminate between different reasons for these changes, such as (1) shifting means, (2) random walk behavior, and (3) constant means but innovations switching from stationary to difference stationary behavior. Almost all procedures presently available in the literature are simultaneously sensitive to all three types of alternatives.

The test statistics under investigation are based on functionals of the partial sums of observations. These cumulative sum–type (CUSUM-type) statistics have limit distributions if the mean remains constant and the errors satisfy the central limit theorem but tend to infinity in the case when any of the alternatives (1), (2), or (3) holds. On removing the effect of the shifting mean, however, divergence of the test statistics will only occur under the random walk behavior, which in turn enables statisticians not only to detect structural breaks but also to specify their causes.

The results are underlined by a simulation study and an application to returns of the German stock index DAX.

This paper discusses nonparametric models for panels of time series. There is already a substantial literature on nonlinear models and nonparametric methods in a regression and time series setting. But almost without exception these developments have been limited to univariate and multivariate models of moderate dimensions. Very little has been done for panels, where the dimension, often corresponding to a number of individuals, typically is very large but where the number of observations for each individual may be small or moderate. It is the aim of this paper to start a systematic theoretical treatment of nonparametric models for panels of time series, in particular on additive models. Extending existing methodology to the panel situation is by no means trivial because already for the parametric case many problems are unsolved. Our estimation approach is based on backfitting methods.

An asymptotic theory is developed for multivariate regression in cointegrated systems whose variables are moderately integrated or moderately explosive in the sense that they have autoregressive roots of the form ρni = 1 + ci/nα, involving moderate deviations from unity when α ∈ (0, 1) and ci ∈ ℝ are constant parameters. When the data are moderately integrated in the stationary direction (with ci < 0), it is shown that least squares regression is consistent and asymptotically normal but suffers from significant bias, related to simultaneous equations bias. In the moderately explosive case (where ci > 0) the limit theory is mixed normal with Cauchy-type tail behavior, and the rate of convergence is explosive, as in the case of a moderately explosive scalar autoregression (Phillips and Magdalinos, 2007, Journal of Econometrics 136, 115–130). Moreover, the limit theory applies without any distributional assumptions and for weakly dependent errors under conventional moment conditions, so an invariance principle holds, unlike the well-known case of an explosive autoregression. This theory validates inference in cointegrating regression with mildly explosive regressors. The special case in which the regressors themselves have a common explosive component is also considered.

The contribution of this paper is threefold. First, a characterization theorem of the subhypotheses comprising the seasonal unit root hypothesis is presented that provides a precise formulation of the alternative hypotheses associated with regression- based seasonal unit root tests. Second, it proposes regression-based tests for the seasonal unit root hypothesis that allow a general seasonal aspect for the data and are similar both exactly and asymptotically with respect to initial values and seasonal drift parameters. Third, limiting distribution theory is given for these statistics where, in contrast to previous papers in the literature, in doing so it is not assumed that unit roots hold at all of the zero and seasonal frequencies. This is shown to alter the large-sample null distribution theory for regression t-statistics for unit roots at the complex frequencies, but interestingly to not affect the limiting null distributions of the regression t-statistics for unit roots at the zero and Nyquist frequencies and regression F-statistics for unit roots at the complex frequencies. Our results therefore have important implications for how tests of the seasonal unit root hypothesis should be conducted in practice. Associated simulation evidence on the size and power properties of the statistics presented in this paper is given that is consonant with the predictions from the large-sample theory.

This note proves the consistency and asymptotic normality of the quasi–maximum likelihood estimator (QMLE) of the parameters of a generalized autoregressive conditional heteroskedastic (GARCH) model with martingale difference centered squared innovations. The results are obtained under mild conditions and generalize and improve those in Lee and Hansen (1994, Econometric Theory 10, 29–52) for the local QMLE in semistrong GARCH(1,1) models. In particular, no restrictions on the conditional mean are imposed. Our proofs closely follow those in Francq and Zakoïan (2004, Bernoulli 10, 605–637) for independent and identically distributed innovations.

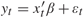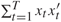Lai and Wei (1983, Annals of Statistics 10, 154–166) state in their Theorem 1 that the estimators of the regression coefficients in the regression , t ∈ ℕ are almost surely (a.s.) consistent under the assumption that the minimum eigenvalue λmin(T) of tends to infinity (a.s.) and log(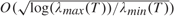λmax(T))/λmin(T) → 0 (a.s.) where λmax(T) denotes the maximal eigenvalue. Moreover the rate of convergence in this case equals . In this note xt is taken to be a particular multivariate multifrequency I(1) processes, and almost sure rates of convergence for least squares estimators are established.