Contents
Articles
Adaptive Estimation in Time Serise Regression Models With Heteroskedasticity of Unknown Form
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 161-187
-
- Article
- Export citation
A Representation of Vector Autoregressive Processes Integrated of Order 2
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 188-202
-
- Article
- Export citation
Semiparametric Generalized Least Squares in the Multivariate Nonlinear Regression Model
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 203-222
-
- Article
- Export citation
Improved Berry-Esseen-Chebyshev Bounds with Statisical Applications
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 223-240
-
- Article
- Export citation
Generic Uniform Convergence
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 241-257
-
- Article
- Export citation
The Bias of Bootstrapped Versus Conventional Standard Errors in the General Linear and SUR Models
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 258-275
-
- Article
- Export citation
A Bootstrap Test for Positive Definiteness of Income Effect Matrices
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 276-292
-
- Article
- Export citation
Photograph Section
The Advisory Board
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 291-292
-
- Article
- Export citation
Book Reviews
Forecasting, Structural Time Series Models and the Kalman Filter, Andrew C. Harvey Cambridge University Press, 1939 - Fore Casting, Structural Time Series Models and The Kalman FilterAdrew C. Harvey Cambridge University Press, 1989
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 293-299
-
- Article
- Export citation
Problems
A Derivation of the Limited Information Maximum Likelihood Estimator
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 301-302
-
- Article
- Export citation
The Three-Choice Multinomial Probit with Selectivity Corrections
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 302-304
-
- Article
- Export citation
Sampling Distributions and Efficiency Comparisons of OLS and GLS in the Presence of Both Serial Correlation and Heteroskedasticity
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 304-305
-
- Article
- Export citation
Characterization of a Positive Semidefinite Matrix
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 305-306
-
- Article
- Export citation
The Maximally Concentrated Unbiased Linear Estimator of β
-
- Published online by Cambridge University Press:
- 18 October 2010, p. 306
-
- Article
- Export citation
Seemingly Unrelated Regression Equations with No Contemporaneous Observations
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 306-307
-
- Article
- Export citation
Simultaneous Equations Bias in Level VAR Estimation
-
- Published online by Cambridge University Press:
- 18 October 2010, p. 307
-
- Article
- Export citation
Partitioned Regression with Rank-Deficient Regressions
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 307-309
-
- Article
- Export citation
Solutions
Global Power of White's Test for Heteroskedasticity
-
- Published online by Cambridge University Press:
- 18 October 2010, p. 309
-
- Article
- Export citation
A Matrix Invariance Problem
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 310-311
-
- Article
- Export citation
Front matter
ECT volume 8 issue 2 Front matter
-
- Published online by Cambridge University Press:
- 18 October 2010, p. f1
-
- Article
-
- You have access
- Export citation
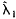 , of the matrix estimate is obtained. This theory applies generally to symmetric, asymptotically normal random matrices. A bootstrap approximation to the distribution of
, of the matrix estimate is obtained. This theory applies generally to symmetric, asymptotically normal random matrices. A bootstrap approximation to the distribution of