Deciding the order of differencing is an important part in the specification of an autoregressive integrated moving average (ARIMA) mode. In most, though not all, cases this means deciding whether to use the original observations or their first differences. Common test procedures used in this context are some variants of autoregressive unit root tests. In these tests, one tests the null hypothesis that the order of differencing is one against the alternative that it is zero. The null hypothesis thus states that the original series is nonstationary and integrated of order one, whereas the alternative assumes that it is stationary. In this paper the situation is reversed so that our null hypothesis states that the original series is stationary, whereas the alternative states that it is integrated of order one. In our approach the use of a differenced series thus means overdifferencing and, consequently, a model with a moving average unit root. Testing for this moving average unit root is the topic of this paper. As discussed by Saikkonen and Luukkonen [26] and Tanaka [31], test procedures obtained for this null hypothesis can also be used to test the null hypothesis that a multivariate time series is cointegrated with a given theoretical cointegrating vector. Since the null hypothesis of cointegration is often of interest and cannot be naturally tested by autoregressive unit root tests, this connection provides an important motivation for the test procedures of this paper.

This paper proposes a new class of heteroskedastic and autocorrelation consistent (HAC) covariance matrix estimators. The standard HAC estimation method reweights estimators of the autocovariances. Here we initially smooth the data observations themselves using kernel function–based weights. The resultant HAC covariance matrix estimator is the normalized outer product of the smoothed random vectors and is therefore automatically positive semidefinite. A corresponding efficient GMM criterion may also be defined as a quadratic form in the smoothed moment indicators whose normalized minimand provides a test statistic for the overidentifying moment conditions.

This paper provides a survey on a class of so-called subspace methods whose main proponent is CCA proposed by Larimore (1983, Proceedings of the 1983 American Control Conference 2). Because they are based on regressions these methods for the estimation of ARMAX systems are attractive as a result of their conceptual simplicity and their numerical advantages as compared to traditional estimators based on criterion optimization. Under the assumption of correct specification the methods provide consistent and asymptotically normal estimates for stationary ARMAX processes where the innovations may be conditionally heteroskedastic and the exogenous inputs are strictly stationary of sufficiently short memory. For stationary autoregressive moving average (ARMA) processes with independent and identically distributed (i.i.d.) Gaussian innovations the estimates are even asymptotically efficient. For I(1) ARMA processes the estimates of both the long-run and the short-run dynamics are consistent without using the knowledge that the data are integrated in the algorithm. Additionally the algorithms provide easily accessible information on the appropriateness of the chosen model complexity. The algorithms include a number of design parameters that have to be set by the user. These include the order of the estimated system. This paper collects up-to-date knowledge on the effects of these design parameters, leading to a number of suggested automated choices to obtain a fully automated estimation procedure.

This paper proposes a general Bayesian framework for distinguishing between trend- and difference-stationarity. Usually, in model selection, we assume that all of the data were generated by one of the models under consideration. In studying time series, however, we may be concerned that the process is changing over time, so that the preferred model changes over time as well. To handle this possibility, we compute the posterior probabilities of the competing models for each observation. This way we can see if different segments of the series behave differently with respect to the competing models. The proposed method is a generalization of the usual odds ratio for model discrimination in Bayesian inference. In application, we employ the Gibbs sampler to overcome the computational difficulty. The procedure is illustrated by a real example.

A vector autoregression with deterministic terms and with no restrictions to its characteristic roots is considered. Strong consistency results for the least squares statistics are presented. This extends earlier results where deterministic terms have not been considered. In addition the convergence rates are improved compared with earlier results.Comments from S. Johansen are gratefully acknowledged.

For use in asymptotic analysis of nonlinear time series models, we show that with (Xt,t ≥ 0) a (geometrically) ergodic Markov chain, the general version of the strong law of large numbers applies. That is, the average converges almost surely to the expectation of φ(Xt,Xt+1,…) irrespective of the choice of initial distribution of, or value of, X0. In the existing literature, the less general form has been studied.We thank Paolo Paruolo (the co-editor) and the referee for valuable comments. Also we thank the Danish Social Sciences Research Council (grant 2114-04-0001) for financial support.

In this note we derive the local asymptotic power function of the standardized averaged Dickey–Fuller panel unit root statistic of Im, Pesaran, and Shin (2003, Journal of Econometrics, 115, 53–74), allowing for heterogeneous deterministic intercept terms. We consider the situation where the deviation of the initial observation from the underlying intercept term in each individual time series may not be asymptotically negligible. We find that power decreases monotonically as the magnitude of the initial conditions increases, in direct contrast to what is usually observed in the univariate case. Finite-sample simulations confirm the relevance of this result for practical applications, demonstrating that the power of the test can be very low for values of T and N typically encountered in practice.

We propose a family of least-squares–based testing procedures that look to detect general forms of fractional integration at the long-run and/or the cyclical component of a time series, and that are asymptotically equivalent to Lagrange multiplier tests. Our setting extends Robinson’s (1994) results to allow for short memory in a regression framework and generalizes the procedures in Agiakloglou and Newbold (1994), Tanaka (1999), and Breitung and Hassler (2002) by allowing for single or multiple fractional unit roots at any frequency in [0, π]. Our testing procedure can be easily implemented in practical settings and is flexible enough to account for a broad family of long- and short-memory specifications, including ARMA and/or GARCH-type dynamics, among others. Furthermore, these tests have power against different types of alternative hypotheses and enable inference to be conducted under critical values drawn from a standard chi-square distribution, irrespective of the long-memory parameters.

The large-sample behavior of one-period-ahead and multiperiod-ahead predictors for a dynamic nonlinear simultaneous system is examined in this paper. Conditional on final values of the endogenous variables, the asymptotic moments of the deterministic, closed-form, Monte Carlo stochastic, and several variations of the residual-based stochastic predictor are analyzed. For one-period-ahead prediction, the results closely parallel our previous findings for static nonlinear systems. For multiperiod-ahead prediction similar results hold, except that the effective number of sample-period residuals available for use with the residual-based predictor is T/m, where T denotes sample size. In an attempt to avoid the problems associated with sample splitting, the complete enumeration predictor is proposed which is a multiperiod-ahead generalization of the one-period-ahead residual-based predictor. A bootstrap predictor is also introduced which is similar to the multiperiod-ahead Monte Carlo except disturbance proxies are drawn from the empirical distribution of the residuals. The bootstrap predictor is found to be asymptotically inefficient relative to both the complete enumeration and Monte Carlo predictors.

We present novel theory for testing for reduction of GARCH-X type models with an exogenous (X) covariate to standard GARCH type models. To deal with the problems of potential nuisance parameters on the boundary of the parameter space as well as lack of identification under the null, we exploit a noticeable property of specific zero-entries in the inverse information of the GARCH-X type models. Specifically, we consider sequential testing based on two likelihood ratio tests and as demonstrated the structure of the inverse information implies that the proposed test neither depends on whether the nuisance parameters lie on the boundary of the parameter space, nor on lack of identification. Asymptotic theory is derived essentially under stationarity and ergodicity, coupled with a regularity assumption on the exogenous covariate X. Our general results on GARCH-X type models are applied to Gaussian based GARCH-X models, GARCH-X models with Student’s t-distributed innovations as well as integer-valued GARCH-X (PAR-X) models.

We consider two tests of structural change for partially linear time-series models. The first tests for structural change in the parametric component, based on the cumulative sums of gradients from a single semiparametric regression. The second tests for structural change in the parametric and nonparametric components simultaneously, based on the cumulative sums of weighted residuals from the same semiparametric regression. We derive the limiting distributions of both tests under the null hypothesis of no structural change and for sequences of local alternatives. We show that the tests are generally not asymptotically pivotal under the null but may be free of nuisance parameters asymptotically under further asymptotic stationarity conditions. Our tests thus complement the conventional instability tests for parametric models. To improve the finite-sample performance of our tests, we also propose a wild bootstrap version of our tests and justify its validity. Finally, we conduct a small set of Monte Carlo simulations to investigate the finite-sample properties of the tests.

This paper is the text of the 1994 Tjalling Koopmans Lecture of the Cowles Foundation. The aim of this lecture was to survey the roles of misspecified models in econometrics. Through 10 stories we show how the misspecifipation problems can be dealt with and how misspecified models can play a positive role in inference processes.

We propose a new kernel estimator for nonparametric regression with unknown error distribution. We show that the proposed estimator is adaptive in the sense that it is asymptotically equivalent to the infeasible local likelihood estimator (Staniswalis, 1989, Journal of the American Statistical Association 84, 276–283; Fan, Farmen, and Gijbels, 1998, Journal of the Royal Statistical Society, Series B 60, 591–608; and Fan and Chen, 1999, Journal of the Royal Statistical Society, Series B 61, 927–943), which requires knowledge of the error distribution. Hence, our estimator improves on standard nonparametric kernel estimators when the error distribution is not normal. A Monte Carlo experiment is conducted to investigate the finite-sample performance of our procedure.We thank Yuichi Kitamura, Yanqin Fan, Joel Horowitz, Roger Koenker, Jens Perch Nielsen, Peter Phillips, Peter Robinson, Tom Rothenberg, and two referees for helpful comments. Financial support from the NSF and the ESRC (UK) is gratefully acknowledged.

Noncausal autoregressive models with heavy-tailed errors generate locally explosive processes and, therefore, provide a convenient framework for modelling bubbles in economic and financial time series. We investigate the probability properties of mixed causal-noncausal autoregressive processes, assuming the errors follow a stable non-Gaussian distribution. Extending the study of the noncausal AR(1) model by Gouriéroux and Zakoian (2017), we show that the conditional distribution in direct time is lighter-tailed than the errors distribution, and we emphasize the presence of ARCH effects in a causal representation of the process. Under the assumption that the errors belong to the domain of attraction of a stable distribution, we show that a causal AR representation with non-i.i.d. errors can be consistently estimated by classical least-squares. We derive a portmanteau test to check the validity of the estimated AR representation and propose a method based on extreme residuals clustering to determine whether the AR generating process is causal, noncausal, or mixed. An empirical study on simulated and real data illustrates the potential usefulness of the results.

This paper introduces various consistent tests for the null of cointegration against the alternative of noncointegration that can be applied to a system of equations as well as to a single equation. The tests are analogs of Choi and Ahn's (1993, Testing the Null of Stationarity for Multiple Time Series, working paper, The Ohio State University) multivariate tests for the null of stationarity and use Park's (1992, Econometrica 60, 119–143) canonical cointegrating regression (CCR) residuals to make the tests free of nuisance parameters in the limit. The asymptotic distributions of the tests are complex but expressed in unified manner by using standard vector Brownian motion. These distributions are tabulated by simulation for some practical cases. Furthermore, the rates of divergence of the tests are reported. Because there are methods for estimating cointegrating matrices other than CCR, it is illustrated for a model without time trends that the tests we introduce work exactly the same way in the limit when Phillips and Hansen's (1990, Review of Economic Studies 57, 99–125) fully modified ordinary least-squares (OLS) procedure is used. Also, is shown that difficulties arise when OLS residuals are used to formulate the tests. Small-scale simulation results are reported to examine the finite sample performance of the tests. The tests are shown to work reasonably wellin finite samples. In particular, it is illustrated that using the multivariate tests introduced in this paper can be a better testing strategy in terms of the finite sample size and power than applying univariate tests several times to each equation in a system of equations.

Cai, Li, and Park (Journal of Econometrics, 2009) and Xiao (Journal of Econometrics, 2009) developed asymptotic theories for estimators of semiparametric varying coefficient models when regressors are integrated processes but the smooth coefficients are functionals of stationary processes. Using a recent result from Phillips (Econometric Theory, 2009), we extend this line of research by allowing for both the regressors and the covariates entering the smooth functionals to be integrated variables. We derive the asymptotic distribution for the proposed semiparametric estimator. An empirical application is presented to examine the purchasing power parity hypothesis between U.S. and Canadian dollars.

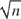A limit theory is developed for multivariate regression in an explosive cointegrated system. The asymptotic behavior of the least squares estimator of the cointegrating coefficients is found to depend upon the precise relationship between the explosive regressors. When the eigenvalues of the autoregressive matrix Θ are distinct, the centered least squares estimator has an exponential Θn rate of convergence and a mixed normal limit distribution. No central limit theory is applicable here, and Gaussian innovations are assumed. On the other hand, when some regressors exhibit common explosive behavior, a different mixed normal limiting distribution is derived with rate of convergence reduced to . In the latter case, mixed normality applies without any distributional assumptions on the innovation errors by virtue of a Lindeberg type central limit theorem. Conventional statistical inference procedures are valid in this case, the stationary convergence rate dominating the behavior of the least squares estimator.

New notions of tail and nontail dependence are used to characterize separately extremal and nonextremal information, including tail log-exceedances and events, and tail-trimmed levels. We prove that near epoch dependence (McLeish, 1975; Gallant and White, 1988) and L0-approximability (Pötscher and Prucha, 1991) are equivalent for tail events and tail-trimmed levels, ensuring a Gaussian central limit theory for important extreme value and robust statistics under general conditions. We apply the theory to characterize the extremal and nonextremal memory properties of possibly very heavy-tailed GARCH processes and distributed lags. This in turn is used to verify Gaussian limits for tail index, tail dependence, and tail-trimmed sums of these data, allowing for Gaussian asymptotics for a new tail-trimmed least squares estimator for heavy-tailed processes.

The contribution of this paper is threefold. First, a characterization theorem of the subhypotheses comprising the seasonal unit root hypothesis is presented that provides a precise formulation of the alternative hypotheses associated with regression- based seasonal unit root tests. Second, it proposes regression-based tests for the seasonal unit root hypothesis that allow a general seasonal aspect for the data and are similar both exactly and asymptotically with respect to initial values and seasonal drift parameters. Third, limiting distribution theory is given for these statistics where, in contrast to previous papers in the literature, in doing so it is not assumed that unit roots hold at all of the zero and seasonal frequencies. This is shown to alter the large-sample null distribution theory for regression t-statistics for unit roots at the complex frequencies, but interestingly to not affect the limiting null distributions of the regression t-statistics for unit roots at the zero and Nyquist frequencies and regression F-statistics for unit roots at the complex frequencies. Our results therefore have important implications for how tests of the seasonal unit root hypothesis should be conducted in practice. Associated simulation evidence on the size and power properties of the statistics presented in this paper is given that is consonant with the predictions from the large-sample theory.

In this paper, we examine the performance of the predictive risk of the Steinrule (SR) and positive-part Stein-rule (PSR) estimators when relevant regressors are omitted in the specified model. The exact formula of the predictive risk of the PSR estimator is derived, and the sufficient condition for the PSR estimator to dominate the SR estimator under a specification error is given. It is shown by numerical computation that the PSR estimator seems to be the best choice among the OLS, SR, and PSR estimators even when there are omitted variables.