INTRODUCTION
Prioritization in any context is used to establish the most attractive alternative, or group of alternatives, as a decision aid for resource allocation. In human and animal health, resources need to be allocated to preventive activities such as biosecurity, vaccination, public education and routine health screening, early warning of disease incursions through surveillance, and instigation of control measures in the case of a disease incursion, among other needs. The choices for resource allocation are effectively limitless; better understanding of epidemiology and pathophysiology have both increased the potential choices for disease prevention and control, and expanding human populations, increased trade and travel, and the emergence and re-emergence of pathogens are further increasing options for resource allocation. However, resources are constrained by finite capital, as well as by the availability of people and the time required to deliver effective prevention and control methods or to undertake research. Therefore, disease prioritization in animal and human health is motivated by the need to ensure that the allocation of limited resources is targeted to achieve the greatest benefit in improving and maintaining human and animal health.
Defining disease importance is difficult. Diseases can have social, economic and environmental impacts, and most diseases cause a variety of impacts that span these broad categories. In addition, impacts vary in scale and are often intangible, and the perception of importance of each impact varies between decision-makers [Reference Wilson, Ward and Garner1]. Economic impacts include the cost of prevention and control and lost productivity due to disease and its perceived risk (e.g. SARS was estimated to cost between US$ 30–100 billion across many sectors, but particularly travel and tourism [Reference Smith2]). Social costs include impacts on individuals and communities – both through the psychological and social impacts of disease burden and loss – and also through altered lifescapes as was seen in the UK foot-and-mouth-disease (FMD) outbreak in 2001 [Reference Mort3]. Environmental impacts include altered ecological balance due to changes in species distribution and abundance [Reference Daszak4]. These areas of impact also overlap – for example, economic impacts can lead to social impacts – which further complicate comparison of disease impacts. To determine the most important diseases for resource allocation, prioritization should not only define and compare the impact of diseases, but also the importance of those impacts to relevant stakeholders, of which there can be multiple groups. In addition, the prioritization process must be transparent and reproducible – and therefore auditable – and provide valid and robust results to direct decision-makers in the development of defensible animal and human health policy [Reference Giesecke5]. Disease prioritization is therefore a complex decision process; the overall objective is important – we want maximum benefit to animal and human health – and there are multiple, and often conflicting, criteria that not only have different scales or are intangible, but also differ in value depending on the perceptions of the decision-maker.
Methods from the discipline of decision science have been used extensively to aid complex decision-making in fields such as information technology and engineering, but have had relatively limited application in health sciences [Reference Bragge, Ehrgott, Naujoks, Stewart and Wallenius6]. However, multi-criteria decision analysis (MCDA), a family of methods from decision science, has been recently used for disease prioritization [Reference Del Rio Vilas7–Reference Havelaar9]. MCDA methods are valuable tools for decision-making in animal and human health, because they account for varying scales and perceptions of impacts using a structured, transparent approach, and aim to give consistent, reproducible results. This review describes the development of disease prioritization as a methodology by illustrating its progression towards methods from the discipline of decision science, particularly MCDA. As a foundation, the requirements of disease prioritization in the context of decision theory are discussed. This is followed by an overview of decision analysis and MCDA relevant to disease prioritization. The development of disease prioritization applications from ad hoc methods to a standardized format is then reviewed. Finally, recent developments and how they aid defensible resource allocation, as well as future directions in disease prioritization are examined.
DECISION THEORY AND THE REQUIREMENTS OF DISEASE PRIORITIZATION
Decision theory forms the basis of decision science and can be divided into three areas: normative, descriptive, and prescriptive [Reference Anand, Pattanaik and Puppe10]. Each of these divisions has important implications for disease prioritization. First, the results of prioritization studies must be defensible, which requires that the method is transparent and logical. This relates to normative decision theory, the basis of which is rational choice. For a decision to be considered rational, an individual should prioritize the disease that maximizes their ‘expected utility’ [Reference Bernoulli11]. ‘Utility’ is a measure of disease importance comprising both the scale and value of impacts to that individual (we note here that for disease we can also refer to this as ‘dis-utility’), and ‘expected’ refers to the individual's estimate of the probability of occurrence of the disease. Normative decisions comply with a set of logical rules, or axioms (Table 1) and can be described by a utility function [Reference Ramsey12, Reference von Neumann and Morganstern13]. Equation (1) shows an example of a utility function in which an individual's expected utility (U) for disease (i) is described as a function of the sum of all the values of the possible overall impacts of the disease (possible disease states, u ij ) and the probability of occurrence of each of those possible disease states (p j ). The axioms that describe rational choice – in particular, completeness and transitivity – have traditionally been used as the ‘gold standard’ to define rational choice, against which decisions are judged as logical; normative decision theory is the dominant underlying theory in decision science, particularly in economics [Reference Jallais, Pradier and Teira14]. In the context of disease prioritization actions need to be defensible, particularly in the face of disease events, when questions are asked such as, ‘given the impact of this event, were the actions justified and should resources have been directed differently?’ Using a decision-aid based on normative theory – therefore complying with the axioms of rational choice – gives rational results, inherently confirming that decisions were logical and that the process was transparent and therefore, auditable [Reference Savage15].
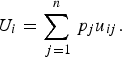 $${U_i} = \sum\limits_{\,j = 1}^n {{\,p_j}{u_{ij}}}. $$
$${U_i} = \sum\limits_{\,j = 1}^n {{\,p_j}{u_{ij}}}. $$
Table 1. Axioms of rational choice associated with normative decision theory, and their relevance to disease prioritization

The second requirement of disease prioritization is that the results should be valid, meaning that they should accurately reflect the priorities of the decision-makers. Normative decision theory would be sufficient to validly describe priorities if decision-makers generally made normatively rational decisions by considering the overall utility of each disease. However, it has been demonstrated that decision-makers systematically violate the axioms of rational choice, and consequently their decisions cannot be validly described with a utility function [Reference Tversky and Kahneman16–Reference Edwards20]. Normative decision models are static and isolated in their decision context; their inability to account for temporal and complex social constraints can result in apparently irrational choices. Moreover, differences in the way the brain reacts to various types of information (e.g. risk and ambiguity) as well as differing decision-making heuristics can also affect choice [Reference Dieckmann, Dippold and Dietrich21, Reference Payne, Bettman and Johnson22]. For example, Hsu et al. [Reference Hsu23] demonstrated that aversion to choice under ambiguity (epistemic uncertainty) generally overrides choice with stated probabilities and suggest that there is a neural basis for choice. Einhorn [Reference Einhorn24] proposed that in some contexts, people use simplifying heuristics to make decisions instead of considering the overall utility of each alternative. Making sense of the apparently illogical choices that humans make is the field of descriptive (or behavioural) decision theory. An example of a descriptive theory of decision-making is prospect theory, developed by Tversky and Kahneman [Reference Tversky and Kahneman16, Reference Kahneman and Tversky25] to account for the psychological effects of framing, loss aversion and anchoring on rational decision-making. Complying with descriptive decision theory is not just important to produce valid results in prioritization, it is also important for designing decision support frameworks to ensure that decision-makers’ preferences are represented as accurately as possible. However, in all decision processes there is a conflict between descriptive and normative decision theory in producing valid results that are also rational, and therefore, defensible.
Prescriptive decision theory attempts to connect the mathematical ideals of normative theory with the psychology of descriptive theory. Throughout the last century many prescriptive theories have been suggested, ranging from ones that follow mainly normative rules – such as von Neumann & Morgenstern's [Reference von Neumann and Morganstern13] game theory that accounted for strategic interaction (including social constraints) in decision making – to others that relax or vary the definitions of the axioms of rational choice to account for choice consistent with descriptive theory. Examples include Simon's [Reference Simon26] concept of bounded rationality to account for constraints in decision-making and models developed by Einhorn [Reference Einhorn24] to describe choice using simplified decision-making heuristics. Recently, it has been suggested that full understanding of decision processes will only be reached through understanding the biological basis of decision-making, and that consequently, the fields of economics, psychology and neuroscience are converging to achieve this goal in a new branch of decision theory called neuroeconomics [Reference Glimcher and Rustichini27, Reference Wilson28]. Until such a state of understanding is reached, there needs to be a balance in achieving validity and rational defensibility through current methods; decision-makers should be aware of this limitation in all decision contexts, not just disease prioritization. The next section gives an overview of available techniques for decision analysis, which aim to convert decision theory into practical decision-making.
DECISION ANALYSIS
Decision analysis is applied prescriptive decision theory [Reference Howard29]. Formal methods for complex decision analysis include decision-trees, monetary-based methods (e.g. cost-benefit analysis), and MCDA [Reference Dodgson30]. MCDA comprises a large group of methods that provide a framework to compare alternatives with diverse and often intangible impacts (broader than monetary-based techniques) by incorporating value judgements on multiple, conflicting criteria with incommensurate scales [Reference Triantaphyllou31]. Consequently, MCDA has become popular for disease prioritization [Reference Del Rio Vilas7–Reference Havelaar9] and we focus on MCDA in this section.
MCDA methods can be divided into multi-attribute decision-making (MADM) and multi-objective decision-making (MODM) [Reference Triantaphyllou31]. MODM methods are designed to find optimal criterion values for decision problems in which a solution is required from a range of continuous objectives [Reference Cohon32]. They are commonly used in fields such as engineering and environmental science, in which resource allocation might be based on finding the optimal combination of a range of resources that have constraints (e.g. cost and site size for hazardous waste disposal [Reference Alumur and Kara33, Reference Giannikos34]). By contrast, MADM methods are used to rank or group alternatives from a finite set of discrete decision alternatives based on comparisons between criteria; therefore, MADM methods are suited to disease prioritization. Diseases are the decision alternatives, and disease attributes that describe disease impacts – such as incidence or severity of clinical signs – are the criteria on which prioritization is based.
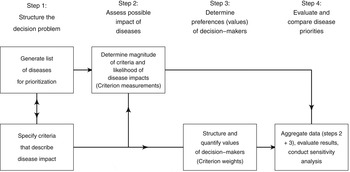
Normative rationality dominates prescriptive decision theory, including MADM. This logical approach is achieved by systematic structuring of the decision problem, and is described in detail by von Winterfeld [Reference von Winterfeldt35] and Keeney [Reference Keeney36]. Figure 1 shows a representation of the steps of decision analysis for disease prioritization, modified from Keeney [Reference Keeney36]. In the case of MADM, the underlying structure of the decision process is the performance matrix (Fig. 2) created in steps 1 and 2 of decision structuring (Fig. 1) [Reference Dodgson30, Reference Triantaphyllou31]. Diseases for prioritization are identified, criteria by which the disease impacts can be described are selected, and criterion measurements are collected for each disease. For example, the criterion ‘case-fatality rate in humans’ might be estimated to be 30% for Japanese encephalitis [Reference Brookes8]. Criterion weights are described separately by evaluating the trade-offs that decision-makers’ are prepared to make between criteria [Reference Keeney37]. For example, the weight of the criterion ‘case-fatality rate in humans’ could be 0.75, following evaluation of ‘case-fatality rate in humans’ in the context of all other criteria relevant to the prioritization. Criterion weights are not disease-specific. The weights allow comparison of criteria with incommensurable scales, and have previously been described as ‘scaling constants’ [Reference Del Rio Vilas, Montibeller and Franco38]. Objective measurements for the criteria for each disease are then aggregated with criterion weights according to the MADM method. Separation of objective measurements of criteria from their subjective weights gives transparency and reproducibility to the process, and also can remove cognitive bias that decision-makers might have when directly evaluating the importance of diseases.
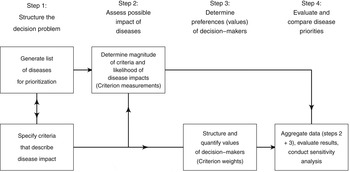
Fig. 1. Schematic representation of the steps of decision analysis for disease prioritization. (Modified from Keeney [Reference Keeney36].)

Fig. 2. Performance matrix for disease prioritization. D, Disease identity, C, criterion; w, weight for criterion; a, measurement for each criterion for each disease. (Modified from Brookes et al. [Reference Brookes8].)
Although all MADM methods follow this structured approach, there are different techniques to evaluate decision-makers’ preferences and aggregate information, and choosing the most appropriate MADM method is not straightforward – in fact making a decision about which decision-making model to use is known as the decision-makers’ paradox [Reference Triantaphyllou and Mann39, Reference Guitouni and Martel40]. Axioms of rational choice are relevant throughout the decision process shown in Figure 1; steps 1 and 2 require that at least two decision alternatives can be defined for which decision-makers can state preferences (axiom of completeness), and steps 3 and 4 maintain that decision-makers preferences should be transitive, monotonic, and independent of irrelevant alternatives. Compliance with normative axioms at steps 3 and 4 is relaxed for methods that follow descriptive theory. The aim in selecting a MADM method should be to match the expected heuristics of the decision-makers, and the most appropriate MCDA method will give the best compromise between normatively rational and descriptively valid results. However, in practice the selection of a MADM method is often based on the decision analyst's familiarity with techniques, the time available, and the perceived complexity of the decision problem [Reference Guitouni and Martel40]. MADM methods include elementary methods (pros-and-cons analysis, maximax and maximin methods, conjunctive and disjunctive methods, lexicographic methods), outranking methods and multi-attribute utility theory (MAUT) or multi-attribute value theory (MAVT) based methods.
Elementary methods reflect simple heuristics using a descriptive approach to decision-making, such as those suggested by Dieckmann et al., Payne et al., and Einhorn [Reference Dieckmann, Dippold and Dietrich21, Reference Payne, Bettman and Johnson22, Reference Einhorn24]. They are non-compensatory in that the primary criterion of concern cannot be outweighed by combinations of other criteria, and the criteria are not weighted. For example, when using lexicographic methods, one criterion is chosen as more important than all the others and initial ordering is based on this primary criterion. Subsequent ordering of choices depends on a secondary criterion, and so on, until all the alternatives have been separated and ordered. Outranking methods are also predominantly descriptive, and are considered to be a more sophisticated extension of elementary methods because they evaluate preferences of decision-makers to assign weights to criteria, reflecting more complex heuristics; there are many methods within this group – also termed the ‘European’ or ‘French school’ of decision analysis – such as ELECTRE (Eliminating Choice and Translating Reality [Reference Roy41]) and PROMETHEE (Preference Ranking Organization Method for Enrichment Evaluations [Reference Brans and Vincke42]).
The MAUT and MAVT group of MADM methods follow a normative approach. MAUT methods for use in decision analysis were developed by Keeney & Raiffa [43] and aggregate information according to a utility function [described in equation (1)]. MAVT methods are a simplification of MAUT methods in that they do not explicitly incorporate decision-makers’ estimates of the probability of occurrence of all possible outcomes of an alternative. MAVT methods have been most commonly used for disease prioritization; subjective weights and objective measurements for the criteria are aggregated for each disease according to a value function. An example of a weighted-sum value function is given [equation (2)] in which the value (D) of a disease (i) is a function of the sum of the weights (w j ) for the criteria combined with criterion measurements (c ij ) for each disease. Examples of the use of MAVT methods include prioritization of emerging zoonoses in The Netherlands [Reference Havelaar9], zoonoses and diseases of food-producing animals [Reference Humblet44], ranking emerging threats in the UK [Reference Del Rio Vilas7] and prioritization of exotic diseases of pigs in Australia [Reference Brookes8]. These methods are considered to be compensatory; diseases are ordered or grouped according to their overall utility, and disease x can be prioritized over disease y based on the aggregated utility or value of different combinations of criteria.
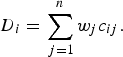 $${D_i} = \sum\limits_{\,j = 1}^n {{w_j}{c_{ij}}}. $$
$${D_i} = \sum\limits_{\,j = 1}^n {{w_j}{c_{ij}}}. $$
Elementary, outranking and MAUT or MAVT methods are not rigid categories. The analytical hierarchy process (AHP) is sometimes categorized as a MAUT method, but because it is based on measurement theory it falls outside the three main groups [Reference Saaty45]. The AHP is implemented in terms of evaluations of weights through direct pairwise comparison of criteria on a Likert-type scale of relative importance. This method has recently been used in a Japanese study to prioritize zoonoses [Reference Kadohira46]. Other methods, such as EVAMIX (EVAlutions with MIXed data), have been developed to include both outranking and MAUT/MAVT methods; EVAMIX was used by Mourits et al. [Reference Mourits, van Asseldonk and Huirne47] to evaluate control strategies for classical swine fever in the European Union.
Currently, there are no guidelines for selection of MADM methods for decision analysis in any field; there is a need to develop procedures to select methods appropriate to the decision context that most accurately reflect decision-makers’ priorities. Until procedures are developed, one of the most important requirements for decision analysis is development of methods to assess the validity of results, particularly when using normative-based methods such as MAUT or MAVT. This step is not included in Keeney's original paper on decision structuring [Reference Keeney36], but is mentioned in his later work on evaluating decision-makers’ trade-offs [Reference Keeney37]. Normative axioms dominate prescriptive theories, and validation to assess the accuracy of results will give an indication of how confident the analyst can be that subsequent recommendations reflect the decision-makers' values. Current methods used for validation are discussed in the section on future directions for disease prioritization.
THE DEVELOPMENT OF DISEASE PRIORITIZATION
This section examines the evolution of disease prioritization in the context of decision analysis. Disease prioritization is already a complex decision problem because the highest priority disease depends on comparison of multiple disease impacts, but complexity increases further because there are usually many decision-makers who represent groups of individuals with potentially diverse objectives [Reference Wilson, Ward and Garner1]. For example, one group might value environmental impacts more than economic costs, or countries or regions might have different values for the social impacts of disease; measuring the utility or value of these impacts across such diverse groups can result in a central measure that is not representative of any group preferences [Reference Brookes48]. This makes assigning utility or value to disease impacts more difficult. Initially, disease prioritization was implemented by simply considering the scale of disease impacts without their utility or value to decision-makers. In a prioritization of diseases in Ghana [Reference Nimo49], the metric ‘healthy days of life lost’ was calculated using objective measurements of disease impact in terms of severity, the average age at disease onset and death, the duration and the level of disability caused by the disease, disease incidence and case-fatality rate. As well as prioritizing diseases by impact on healthy days of life lost, this metric was used to assess the benefits of various health improvement procedures, to select those that could save the greatest number of healthy days of life relative to the cost of the procedure. Following this study, disease prioritization moved in two directions: further development of metrics to quantify disease burden [e.g. disability adjusted life years (DALYs), used by the World Health Organisation (http://www.who.int/healthinfo/global_burden_disease/metrics_daly/en/)], and development of an approach for disease prioritization structured according to decision-science methodology to reflect the value of disease to those directing the prioritization.
Disease prioritization to incorporate the value of disease impact to those directing the prioritization has developed at regional, national and industry levels. Initially, studies were not structured to separate disease criterion measurements and criterion weights. A Canadian study initiated in 1987 prioritized communicable diseases for national surveillance using a point scoring system in which decision-makers directly scored each disease against ordinal scales of severity for each criterion [Reference Carter50]. Similar scoring systems were also used in the 1990s to establish priorities for communicable disease surveillance in Europe [Reference Weinberg, Grimaud and Newton51] and resource allocation in England [Reference Rushdy and O'Mahony52], as well as for prioritization of non-foodborne zoonoses in France [Reference Valenciano53] and communicable diseases for surveillance in a repeat of the original 1987 Canadian study [Reference Doherty54]. Carter et al. [Reference Carter55] had noted that a rational system was needed for disease prioritization, and Rushdy & O'Mahony [Reference Rushdy and O'Mahony52] stated that prioritization should be an ‘open process of communication and consultation’. The overall benefit of these early studies was to introduce disease prioritization as a systematic process to direct resources through consultation between decision-makers.
In a commentary in The Lancet, Giesecke [Reference Giesecke5] noted that transparency was one of the main challenges in disease prioritization. Subsequently, prioritization studies introduced concepts from decision analysis to improve transparency by separating criterion measurements from criterion weights. Examples include three European studies: prioritization of foodborne zoonoses by Cardoen et al. [Reference Cardoen56], communicable disease prioritization by Balabanova et al. [Reference Balabanova57] (initiated by Krause et al. [Reference Krause58] and reviewed by Gilsdorf & Krause [Reference Gilsdorf and Krause59]), and animal and zoonotic diseases by Humblet et al. [Reference Humblet44]. As well as incorporating problem structuring, each of these studies aggregated information based on MAVT using a linear weighted sum value to give a score for each disease. Overall, this led to improved transparency by clearly separating decision-makers’ subjective opinions regarding the value of criteria from measurements for individual diseases, as well as reducing opportunity for cognitive bias that can arise when directly valuing diseases.
In addition to structuring prioritization studies to separate criterion measurements and weights, it is essential to evaluate decision-makers preferences to validly reflect their priorities (step 3, Fig. 1). In a review of common mistakes made during this step, Keeney [Reference Keeney37] highlighted the importance of evaluating preferences by asking decision-makers to make trade-offs between criteria, as well as describing some of the difficulties encountered at this stage. In particular, it was noted that not knowing the context of the trade-off (the scale and potential range of consequences) can lead to incorrect value judgements, potentially making the decision analysis results invalid. This is consistent with Steele et al. [Reference Steele60], who showed the importance of integrating the scale of criterion measurements with value judgements of the criteria; the authors demonstrated that the order of alternatives could be changed by simply changing the scale of criterion measurements while values judgements were held constant. Some aspects of the importance of correctly evaluating decision-makers’ preferences (as well as other challenges associated with disease prioritization) are also described by Del Rio Vilas et al. [Reference Del Rio Vilas, Montibeller and Franco38]. Ultimately, the results of decision analyses are valid only through good fortune if decision-makers’ preferences are elicited independently of scale and context; without validation, the accuracy of the results of these prioritizations cannot be assessed.
In a study to develop a framework for prioritization of emerging threats and vulnerabilities for the Department for the Environment, Food and Rural Affairs (Defra) in the UK, Del Rio Vilas et al. [Reference Del Rio Vilas7] further advanced prioritization in health settings by using established decision analysis methods to both structure the prioritization and also evaluate trade-offs. Normative rationality was provided by the MADM structure of the prioritization that separated disease measurements from decision-makers' values for criteria, and aggregated information using a linear weighted sum model based on MAVT. Swing-weighting was used to quantify disease experts' subjective preferences for the importance of criteria. This is an established method to directly weight criteria [Reference von Winterfeldt and Edwards61], and ensured that trade-offs were evaluated within the context of the decision problem and the scale of the criteria. Swing-weighting has been used previously in animal health for prioritization of control measures for contingency planning for an FMD incursion [Reference Mintiens and Vose62]. Evaluation of decision-makers’ preferences in this way is more likely to accurately reflect decision-makers' preferences and the results are more likely to be repeatable within the same group. MADM based prioritizations using swing-weighting are suited to small groups of decision-makers in the way that the Delphi technique is suited to small group expert-opinion elicitation. While the methods for traditional MCDA are repeatable within groups and reproducible across groups, reproducibility of results across groups are dependent on the selection of decision-makers in the context of the disease prioritization.
Both of these previous studies used linear weighted sum models to represent decision-maker heuristics [equation (2)] [Reference Del Rio Vilas7, Reference Mintiens and Vose62]. This model is commonly used because MAUT- or MAVT-based models with dependent or nonlinear preferences between criteria are complex to implement [Reference Dodgson30]. Although the linear weighted sum model is straightforward, an assumption of independent preferences between criteria is essential, which is restrictive and might not validly describe decision-makers’ heuristics; recent disease prioritization studies have used techniques to circumvent this assumption. These studies used probabilistic inversion [Reference Brookes8, Reference Havelaar9, Reference Brookes48] and conjoint analysis [Reference Ng and Sargeant63, Reference Ng and Sargeant64] to indirectly derive criterion weights. Decision-makers ranked groups of constructed disease scenarios that were designed to force trade-offs between different criteria. Variation in decision-makers' preferences was modelled and the studies using conjoint analysis quantified this variation to allow generalization of the results to the wider population; further development is required to allow this with probabilistic inversion. Each study assessed whether decision-makers' heuristics were normatively rational by checking that choices were transitive [Reference Brookes8, Reference Brookes48], and maximized utility [Reference Ng and Sargeant63, Reference Ng and Sargeant64]. Also, the online surveys used to elicit preferences for criteria presented realistic disease scenarios using non-technical terminology, which enabled participation of decision-makers who were not disease experts [Reference Brookes8, Reference Brookes48, Reference Ng and Sargeant63, Reference Ng and Sargeant64]. The main advantage of these methods is that they enable out-of-sample validation in which the fitted model can be used to predict decision-makers' rankings of a set of disease scenarios other than those used to fit the model [Reference Neslo and Cooke65]. Assessing the validity of models allows assessment of the accuracy of predictions, and further aids defensible resource allocation in addition to the systematic, transparent and reproducible methodology provided by decision analysis. A disadvantage of probabilistic inversion and conjoint analysis is that they rely on statistical methods to produce valid results and therefore, depending on model complexity, potentially require large numbers of participants, making them unsuitable for use in small-group decision-making.
FUTURE DIRECTIONS FOR DISEASE PRIORITIZATION
To date, out-of-sample validation has shown that disease prioritization models have variable validity [Reference Havelaar9, Reference Brookes48, Reference Neslo and Cooke65–Reference Teck67]. It is unclear whether limited validation occurs because validation methods are inadequate, or whether the models are poor representations of decision-makers’ heuristics; it is difficult to develop validation methods given this structural uncertainty. Currently, MADM methods are selected on an empirical basis, and most disease prioritizations have used MAVT-based methods with a linear weighted sum model. There is a requirement to develop systematic science-based processes to select models for prioritization to improve our ability to accurately describe decision-makers' heuristics, and concurrently allow development of validation techniques, particularly for disease prioritizations such as MAUT-/MAVT-based methods which are currently not validated. At a minimum, validation provides an indication of the accuracy of model predictions. Concurrent development of model selection and validation should result in more predictive models that are therefore more valuable decision tools.
Sources of variability in disease prioritization results include heterogeneity in decision-makers’ values, as well as uncertainty and variability associated with disease impacts. In the case of MAUT methods, there is also variation in the decision-makers’ expected probability of occurrence of disease. Sensitivity analysis can be used to examine the robustness of prioritization results to variability in inputs. Similar to other methods for disease investigation (such as risk analysis and disease modelling), prioritization is subject to the same challenges in uncertainty and variability in disease measurements. Uncertainty and variability associated with disease impacts has been accommodated in disease prioritizations by including multiple disease scenarios or ranges of uncertainty or variability across levels of criterion measurements. Disease measurements can change over time, and should be updated as new information arises, especially if the results from the prioritization are highly sensitive to variation in criterion measurements. However, unlike other methods for disease investigation, prioritization results are dependent on, and can also be sensitive to, decision-makers subjective values. Subjective values are likely to be dynamic within individuals – changing as experiences change – and heterogenous throughout groups of decision-makers, particularly if the scope of the decision problem is wide. Scope in this context has two sources: the breadth of the problem (e.g. prioritization of diseases affecting more than one species has broader scope) and the diversity of the decision-makers (e.g. a prioritization study that includes multiple groups of stakeholders also has broader scope). Variation in decision-makers' preferences has been modelled using conjoint analysis and probabilistic inversion [Reference Brookes8, Reference Havelaar9, Reference Ng and Sargeant63, Reference Ng and Sargeant64]. In a study in which pig producers prioritized both zoonoses and diseases that only affect livestock it was found that producers preferences were divided by these disease types and that each group of stakeholders’ preferences were better represented using a model specific to each group [Reference Brookes48]. Although the feasibility of representing multiple stakeholder groups is dependent on the prioritization context, decision-makers should be aware of the challenges associated with increasing the scope of disease prioritizations – it is possible to produce results that are not representative of any stakeholder group or disease type [Reference Brookes8]. In addition, decision-makers’ preferences should be re-assessed periodically to ensure that preferences are current. What constitutes an adequate time-frame for re-assessment is again dependent on the prioritization context. Doherty et al. [Reference Doherty54] repeated a prioritization of diseases in Canada after a period of 10 years and found changes in priorities [Reference Carter50] – appropriate time-frames will become clearer as disease prioritizations become more commonly used and repeated.
The final potential source of variability, the probability of disease occurrence, has not been explicitly modelled in disease prioritizations that have been structured according to decision analysis methods. Utility functions, by their definition, include a measure of probability through evaluation of decision-makers’ expected probability of occurrence of either individual or grouped criteria, or the overall probability of occurrence of the decision alternative [Reference Keeney and Raiffa43]. However, in the context of disease prioritization, utility functions (MAUT-based methods) have been simplified to value functions (MAVT-based methods) in which the outcome is simply a measure of impact for a particular disease. If MAUT methods are to be developed for disease prioritization it is essential that the sources of variation are explicitly modelled, for example by producing a two- or three-dimensional output. The results of prioritization are potentially misleading if the probability of occurrence, uncertainty of impacts and variation in decision-makers' preferences are not differentiated. Ultimately, however, disease prioritization is a decision aid that must provide decision-makers with a foundation from which they can make informed, defensible choices. Given the many pathways by which a disease can occur, and the associated probabilities of each step of a pathway, adding complexity through inclusion of the probability of disease occurrence as a utility model is unlikely to aid communication between decision analysts and decision-makers. Human and animal health have well established methods for risk assessment – for example the framework for import risk analysis for animals and animal products [68]. Prioritization can be considered the first step in a chain of investigations that use a range of methods (e.g. risk analysis and disease modelling) to identify the highest impact diseases that have a perceived high probability of occurrence given those impacts, for which resource allocation will make a valuable contribution in reducing the actual or potential disease burden. Whether for exotic or endemic diseases, resource allocation needs to achieve the greatest benefit in reduction of potential or existing disease burden. This requires a secondary process beyond prioritization. MODM methods can ensure that resources are allocated to the optimum combination of prevention and mitigation strategies given the potential benefits and constraints – such as economic cost, welfare implications, and time and human resources required for implementation – of each strategy [Reference Dodgson30]. There is potential to add MODM to the range of tools available for decision-making in the context of disease prioritization.
CONCLUSION
MADM methods from decision analysis have gradually been applied to disease prioritization with the objective of improved transparency of method and validity of results. The key points in applying these methods are structuring the prioritization to separate objective measurements from subjective values for the disease criteria, and assessing decision-makers' preferences through value trade-offs between criteria within the decision context. Ideally, prioritization results should be both rational and valid. However, normative and descriptive decision theories conflict and there is a balance in prescriptive decision analysis in achieving rationality and validity. Currently, selecting an appropriate MADM method is as much art as science, and generally prioritization at regional, national and industry levels has taken a normative approach, using MAVT based on a linear weighted sum models for aggregation of information. This approach is logical and consistent, and provides results that are rational, and therefore auditable and defensible. Recently, weighting of criteria using probabilistic inversion has enabled validation of results to provide an indication of the accuracy of predictions, and conjoint analysis has enabled assessment of the reproducibility of results across similarly representative samples from the same group of stakeholders. However, further research to select the most appropriate MADM method and aggregating function is required and decision-makers should be aware of the limitations of prioritization in validly reflecting decision-makers’ heuristics. Structuring prioritization studies to separate objective disease measurements from subjective values of disease impacts is a step that is now consistently applied. However, evaluating preferences by assessing the trade-offs that decision-makers are prepared to make between criteria is not consistently undertaken. It should be noted that criterion weights are not direct measures of importance of criteria and cannot be evaluated as such – evaluation of criterion weights within the decision context is required to scale incommensurate criteria to their relative comparative values and produce a valid overall disease score. It is an essential step and should not be seen as adding unnecessary complexity to the process. Although MADM methods might be more difficult to explain to decision-makers in the short term, they are likely to become more accepted through use, and – of greater importance – decision-makers can be more confident that subsequent resource allocation reflects current disease priorities.
ACKNOWLEDGEMENTS
The first author was funded as a PhD student by Australian Pork Limited (project no. 2010/1000.381).
DECLARATION OF INTEREST
None.