INTRODUCTION
Annual vaccination of children with trivalent inactivated influenza vaccination (TIV) is recommended in some countries as a public health measure to reduce the incidence of influenza infections [Reference Bodewes, Kreijtz and Rimmelzwaan1], but there have been few previous studies exploring the variation in immunogenicity of this vaccine in children. Understanding the degree of variation in antibody response, a correlate of protection [Reference Ohmit2], and the extent to which this variation is due to the age of the child, the child's vaccination history, and which influenza virus subtypes are included in the vaccine, could help with assessing vaccine effectiveness [Reference Ng3, Reference Ng4] and the cost-effectiveness of vaccination programmes [Reference Meltzer5].
Although immunogenicity is related to protection from infection, in this paper we focus purely on improving understanding of the trajectories of influenza antibodies following vaccination, because this could help in improving inferences on influenza incidence in the community in seroepidemiological studies. The current standard for determining influenza infection using paired serology is the presence of a fourfold rise in antibody titre. However, it has been proposed that this method will not reveal all infections [Reference Cauchemez6], and conversely that due to boosting of titres by vaccination that not all fourfold rises are due to infection, while measurement error can also cause noise. Post-vaccination titre dynamics will form part of a model of titre dynamics that will allow for better estimation of influenza incidence using serological data.
In 2008–2009 [Reference Cowling7] and 2009–2010 [Reference Cowling8] we conducted randomized controlled trials of TIV in 119 and 796 children aged 6–17 years. respectively, in Hong Kong. In previous work we reported on the immunogenicity of repeated administration of TIV vs. placebo in 64 children who participated in both studies [Reference Ng3], and further examined the role of age and previous vaccination on immunogenicity of TIV in the 796 participants in the 2009–2010 study [Reference Ng4]. In the present study, we describe a new multivariate Bayesian model that can be used to quantify the extent, variability and correlations of antibody rises after receipt of TIV in children, and we illustrate the model by re-analysing data from our 2009–2010 study.
METHODS
Subjects
A randomized controlled trial of TIV was conducted from August 2009 to December 2010 (ClinicalTrials.gov identifier: NCT00792051) [Reference Cowling8]. Eligible participants were children aged 6–17 years living in Hong Kong. Participants were randomized to receive TIV or saline placebo (repackaged to maintain blinding) between August 2009 and February 2010 and then followed up until September–December 2010. The TIV used in the study included the strains A/Brisbane/59/2007(H1N1), A/Brisbane/10/2007(H3N2), and B/Brisbane/60/2008 (Victoria lineage). Serum specimens were collected immediately prior to vaccination and again 1 month after vaccination. The study was approved by the Institutional Review Board of the University of Hong Kong. Proxy written consent from parents or legal guardians was obtained for all participants (who were aged 6–17 years), with additional written assent from those aged 8–17 years.
All antibody titres were measured by haemagglutination inhibition (HI) assays. The test was performed using standard methods as detailed in the WHO reagent kit. The serum specimens were tested in serial doubling dilutions from an initial dilution of 1:10. Further details are available elsewhere [Reference Cowling7]. The titres measured were against the three strains included in the TIV vaccine, plus the influenza B virus that had prevailed in the preceding season B/Florida/4/2006 (Yamagata lineage) and the pandemic strain A/California/7/2009(H1N1), as detailed previously [Reference Ng4, Reference Cowling7].
Statistical analysis
We specified a multivariate Bayesian statistical model to describe the changes in antibody titre levels following vaccination. Using a Bayesian model allows for the explicit incorporation of prior information or knowledge into the analysis, and allow for true understanding of the uncertainty regarding the values of model parameters, unlike traditional confidence intervals [Reference Greenland9]. Under the model, the logarithms of the post-vaccination antibody titres of a subject follow a multivariate Normal distribution, with the mean of the distribution equal to the logarithm of the subject's baseline titres plus a vector representing the average change in antibody titres following vaccination. A variance-covariance matrix of the distribution was also estimated, which reflects how deviations from the average titre rises are correlated between different antibody titres. For example, if subjects with a higher than average baseline titre against the 2009 pandemic influenza virus also have a higher than average titre against the seasonal A(H1N1) influenza subtype, this higher correlation will be reflected in the matrix. The observed titres are then normally distributed on the logarithm scale around the true titres.
The model can be described with the following equations:
where MN 5 represents a five-dimensional multivariate Normal distribution due to there being five HI assays, χ it is the vector of observed antibody titres before (t = 1) and after (t = 2) vaccination for each subject i, θ it is the vector of true antibody titres before (t = 1) and after (t = 2) vaccination for each subject i, δ is the vector of means of the antibody titre changes after vaccination, Σ t is the 5 × 5 variance-covariance matrix of titres at time t and M is the variance-covariance matrix of measurement error. Using a Bayesian model enables point estimation of the parameters δ, Σ1, Σ2 and M and their credible intervals. For comparison and validation, we estimated these parameters for children who were randomly allocated to placebo, and also fitted this model on the linear scale instead of the logarithm scale.
We also fitted regression models to investigate how the rises of each titre differed by each age, sex and self-reported vaccination history, so that
where δ a,s,d is the vector of titre rises for each combination of age (i.e. 6–8 years or ⩾9 years), sex, and seasons of previous influenza vaccination (not being vaccinated during the previous 2 years, or being vaccinated for the 2007–2008 season, for the 2008–2009 season, or for both of these years). This was modelled as both a main effects model
and a saturated model where a separate δ a,s,v was estimated for each combination of age, sex, and vaccination history. The posterior probability of each model was used to determine which model to select. When the value of a covariate for a subject was missing, it was simulated in the analysis in proportion to its observed frequency.
For each parameter, we specified uninformative prior distributions across the range of possible values. The posterior distributions were estimated with a Hamiltonian Monte Carlo sampler using the package ‘rstan’ in R (R Foundation for Statistical Computing, Austria). For each model and dataset, two chains of 60 000 iterations each were simulated to assess convergence, with the first 10 000 iterations of each chain used for burn-in, followed by 50 000 iterations used for analysis. Convergence was assessed using the potential scale reduction statistic [Reference Gelman and Rubin10]. We validated this model by plotting the difference between observed and predicted titre rises and assessing model fit.
RESULTS
In total, 479 participants were randomized to receive TIV, and all participants received the vaccine. Pre-vaccination sera could not be collected for five participants and in addition post-vaccination sera were not collected for 10 further individuals, and these 15 participants were excluded from further analysis. Table 1 shows the characteristics of the 464 subjects included in the analyses, of whom 52% were male, and 35% were aged 6–8 years with the remainder aged 9–17 years. Vaccination status was available for all but 12 of the subjects, with the majority reporting no receipt of TIV during the previous 2 years.
Table 1. The characteristics of 452 subjects who received trivalent inactivated influenza vaccination
Figure 1 shows the geometric mean estimates and 95% credibility intervals (CrI) for the multiplicative rises in the various titres following vaccination, i.e. exp(δ) using the notation in the Methods section. The strongest rises were for the antibody titres against two seasonal influenza A viruses, with those against seasonal A(H1N1) rising on average 10·1-fold (95% CrI 8·4–12·2) and those against the seasonal A(H3N2) variety rising 13·4-fold (95% CrI 11·1–16·2). The geometric mean titre rise against the B/Brisbane (Victoria lineage) strain included in the TIV was 7·9-fold (95% CrI 6·7–9·5) while that against the previous season's prevalent B strain B/Florida (Yamagata lineage) was 4·2-fold (95% CrI 3·6–4·9). The geometric mean fold rise in titres against pandemic A(H1N1) was 1·5 (95% CrI 1·3–1·7).
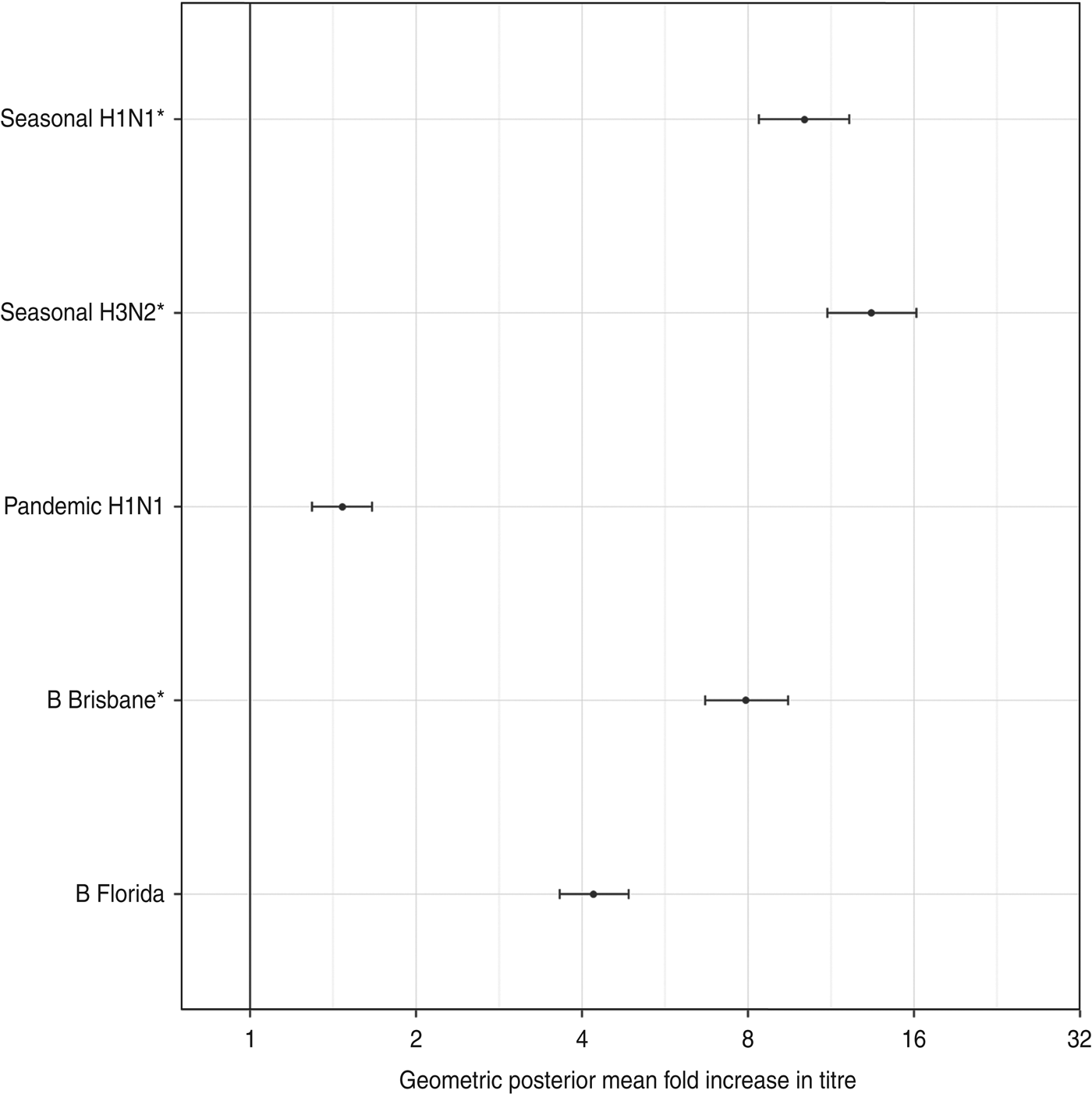
Fig. 1. The geometric mean (with 95% credibility intervals) fold rises following vaccination of all assays. The means and intervals are shown on a logarithmic scale. The three strains included in the trivalent inactivated influenza vaccine are indicated by asterisks.
Figure 2 shows the estimated geometric standard deviations of the titre rises, along with their 95% credibility intervals. There was less variability in titre rises against the influenza type A viruses than type B viruses.
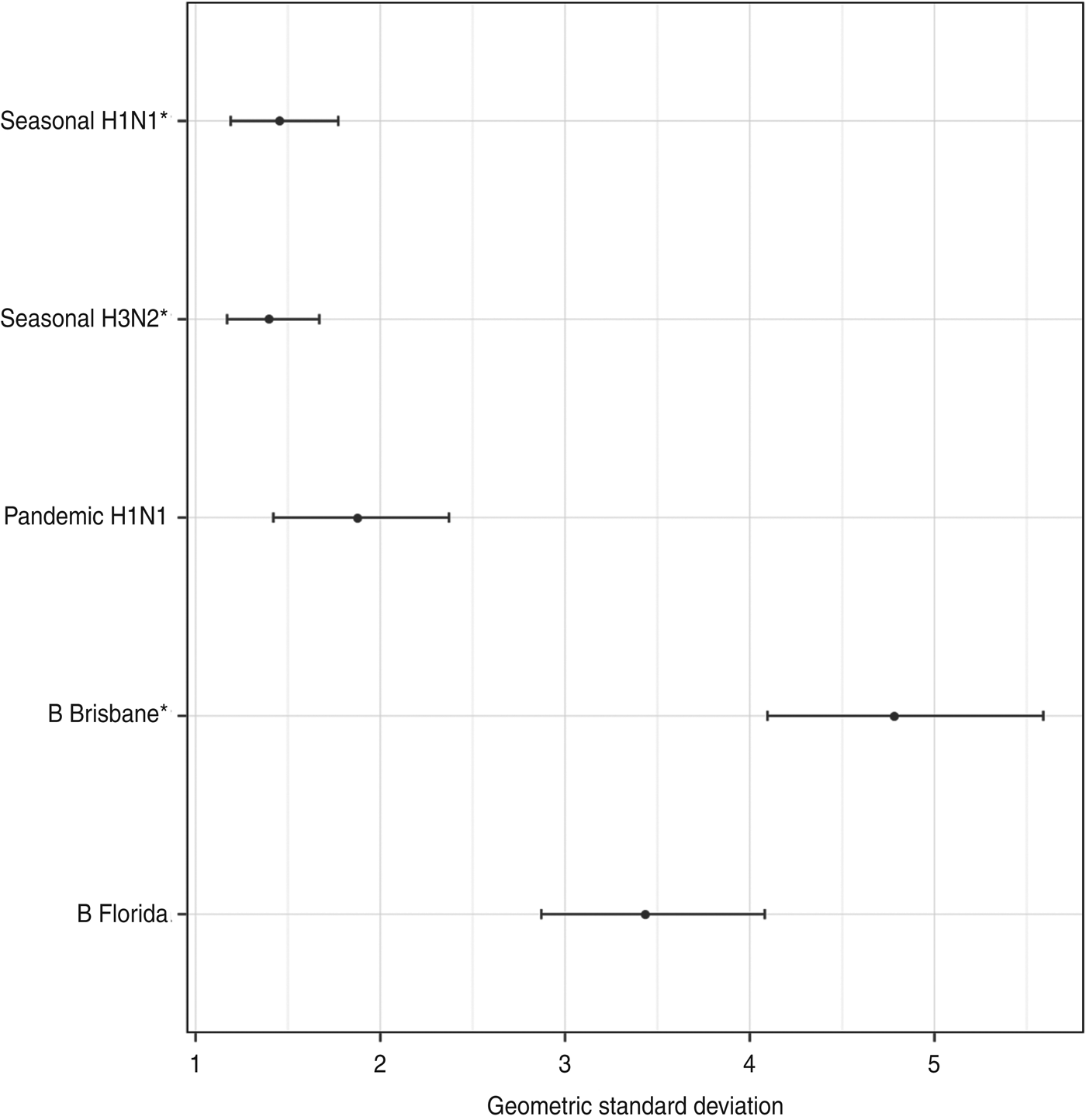
Fig. 2. The geometric standard deviation (with 95% credibility intervals) of each titre's rise after vaccination. These represent the diagonal elements of Σ, the variance-covariance matrix of antibody rises. The three strains included in the trivalent inactivated influenza vaccine are indicated by asterisks.
The correlations between the titre rises are shown in Figure 3. The most closely correlated titre rises are those for the antibodies against the two B lineages. The antibody rise against seasonal A(H1N1) had very low correlation with any of the other antibodies except for seasonal A(H3N2).

Fig. 3. The correlations between the antibody titre rises. The darker squares indicate higher correlation. The three strains included in the trivalent inactivated influenza vaccine are indicated by asterisks.
There was some indication of different antibody dynamics following vaccination between children with different ages, sexes and vaccination histories. The simpler model, where the titre rises were estimated as a sum of age, sex, and vaccination history effects, had a higher posterior probability than the saturated model where the mean titre rises were modelled independently for each combination of the factors. The posterior geometric mean titre rise ratios for each factor and virus subtype are shown in Figure 4. The most significant differences in antibody titre behaviour were in the seasonal A virus titres between those who were vaccinated in previous seasons and those were not, with the former rising by only around a quarter as much as the latter, with smaller rises for more recent vaccinations. There was also a statistically significant difference in the titres against the B/Brisbane (Victoria lineage) included in the TIV between those of different sexes and ages, with boys and older children exhibiting higher rises. There were also significant or near-significant effects of sex on pandemic A(H1N1) titres, with boys experiencing higher titre rises. Significant effects of vaccination history were also observed for the B/Florida (Yamagata lineage) antibody titres, with children previously vaccinated during the 2008–2009 season, when the TIV included this strain, having higher titre rises against this subtype than children who were either vaccinated only during the 2007–2008 season or both the 2007–2008 and 2008–2009 seasons.

Fig. 4. The posterior geometric mean ratio in rises between complementary subpopulations for each assay. The three strains included in the trivalent inactivated influenza vaccine are indicated by asterisks.
Figure 5 shows the distribution of differences between the predicted logarithms of the antibody rises for each study participant and their observed antibody titre rises. The normal distribution of the errors around zero indicates that the model is well specified.

Fig. 5. The distributions of the differences between observed and predicted logarithms of titre rises for each subtype. The distributions appear to follow normal distributions, consistent with the model specification. The three strains included in the trivalent inactivated influenza vaccine are indicated by asterisks.
There was a low risk of natural influenza infection during the month between the two titre measurements, according to analysis of children in the placebo arm of the study. Figure 6 shows the geometric mean-fold antibody rises for each titre in the placebo arm. All titres showed minimal rises, with only pandemic A(H1N1) titres showing a significant geometric mean-fold rise, of 1·3 (95% CrI 1·1–1·5). This indicates that the titre rises observed in the vaccination arm are due almost entirely to the effects of vaccination.
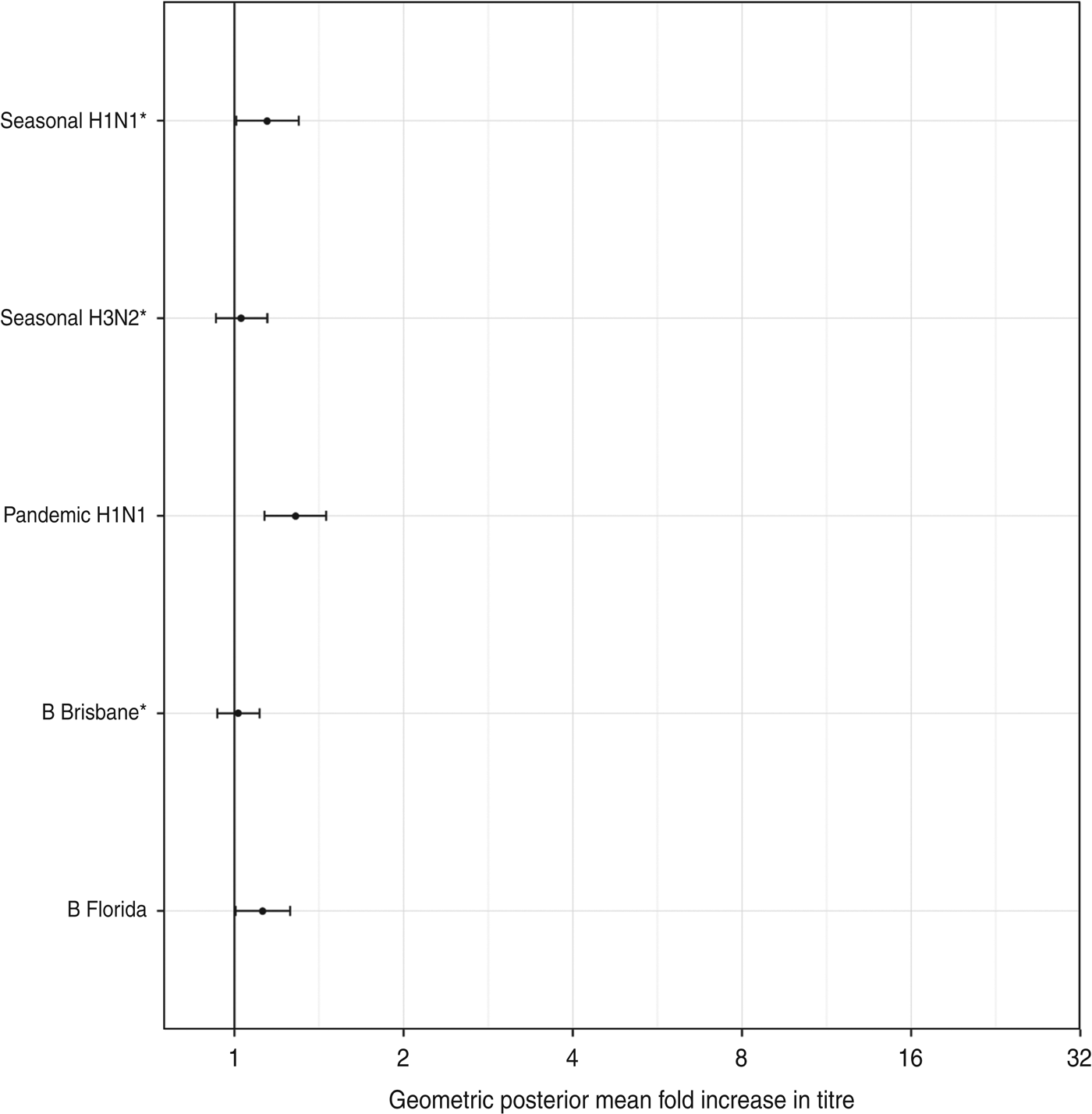
Fig. 6. The geometric mean (with 95% credibility intervals) fold rises of all titres for subjects in the placebo arm. The means and intervals are shown on a logarithmic scale. The three strains included in the trivalent inactivated influenza vaccine are indicated by asterisks.
The same model was attempted on the linear instead of the logarithmic scale but the model fit was extremely poor, and we do not present its results here. Further details are available on request from the corresponding author.
DISCUSSION
We have described the development and application of a Bayesian model for antibody titre rises following vaccination. We used the model to identify substantial variation and correlation in antibody titre rises against different strains following TIV vaccination in children, and explored how factors such as age, sex, vaccination history and the subtypes included in the vaccine affect the behaviour of post-vaccination antibody titre rises [Reference Huijskens11, Reference Seidman12]. This will help in future work that relies on the immunogenicity of TIV in a population of children, such as evaluations of annual vaccination of schoolchildren, as well as increasing our understanding of antibody titre dynamics following vaccination which is relevant for seroepidemiological studies.
Using a Bayesian model for the analysis of immunogenicity data is uncommon, with a few exceptions (e.g. [Reference Coudeville13]). A Bayesian model leads to easier analysis of complex models by allowing for the explicit modelling of the uncertainties of model parameters before and after observing data [Reference Greenland9]. Applying Bayesian models is generally technically more difficult than frequentist models, but can be implemented relatively straightforwardly using Bayesian modelling languages such as BUGS [Reference Lunn, Spiegelhalter, Thomas and Best14] and stan [15].
There are some limitations in our study. First, we could not investigate the extent to which other factors affected antibody dynamics, particularly pre- or post-vaccination infection by influenza or other respiratory diseases, as all RT–PCR-confirmed infections in the study occurred after both antibody titre measurements. The effect of infection on post-vaccination antibody titres is known to be different from that on titres where no vaccination had taken place that season [Reference Ohmit2], but the exact nature of the difference is still not known. Second, the assays used for this study determined antibody levels by the standard method of doubling the dilution of serum until haemagglutination is detected. The exact titre levels are therefore not available and the titre levels used in the analysis must be considered to be approximations. Additionally, measurement error could not be estimated in this study due to lack of repeated measurements [Reference Cauchemez6]. We identified a low risk of natural influenza virus infections during the period between administration of TIV and collection of post-vaccination sera (Fig. 6). Comparison of the antibody responses of the TIV recipients (Fig. 1) with the placebo recipients (Fig. 6) is consistent with little to no cross-reactivity of TIV with 2009 pandemic influenza A(H1N1), as has been reported elsewhere [Reference Hancock16]. Last, we used only the data from the main study in 2009–2010 and not the pilot study in 2008–2009 because this would add another confounder.
The results obtained here are consistent with the previous analysis reported by Ng et al. [Reference Ng4] concerning the effect of age, which also found that younger children had a significantly lower influenza B antibody response. Our model allowed us to further assess the effect of sex on antibody response. We found higher antibody rises in boys compared to girls for antibodies to the two influenza B viruses tested as well as pandemic A(H1N1), but not the two seasonal influenza A viruses. Re-analysis of the data revealed that boys aged both over and under 9 years had significantly higher or non-significantly different rises than girls across all subtypes tested, these rises were significantly lower in older boys for the subtypes included in the TIV. We found no previous discussion of sex differences in humoral antibody responses to influenza vaccination in children. It is well known that there are sex differences in both innate and adaptive immune responses [Reference Pennell, Galligan and Fish17]. A literature review of sex differences in vaccine response [Reference Klein, Jedlicka and Pekosz18] found six studies where adult females have a stronger humoral response to TIV. It is possible that female adults have a stronger antibody response to vaccination while in children boys have the higher titre rises, as seems to be the case for measles vaccination [Reference Cook19]. Further investigation of this phenomenon is warranted, for example how sex-specific hormonal changes after puberty might affect immunity and vaccine responses.
Even though the recorded antibody titres analysed in this paper could only take one of several discrete values, we modelled the logarithms of the observed antibody titre rises as following a multivariate normal distribution, which is a continuous probability distribution [Reference Johnson and Wichern20]. This reflects that the underlying titre levels are on a continuous scale, and is the approach used by other modellers of antibody titres [Reference Coudeville13]. Plotting the distribution of the difference between the observed and predicted antibody titre rises (Fig. 5) shows that this is a reasonable model. The model presented in this paper is inspired by the usage of ‘n-fold rises’ when discussing the behaviour of antibody titres following vaccination or infection. However, it might be the case that the behaviour of antibody titres after vaccination or infection depends on their baseline level. This hypothesis, which can be incorporated into the model considered here, will be tested in future work.
The model presented here will form a component of a more comprehensive modelling framework for antibody titre kinetics that can improve inferences on infection status and incidence of influenza using longitudinal serological measurements. The approach developed here can be extended to incorporate as many virus types and assays as desired, such as new assays that were not available for this study, for example protein microarrays [Reference Koopmans21]. Future work will include understanding the behaviour of humoral antibody titres after influenza infection, with and without vaccination, and the rate of waning after infection or vaccination. Understanding the distribution of antibody titre dynamics will have profound policy implications, by increasing accuracy of the estimates of the incidence of influenza in the population as well as providing for uncertainty bounds which can be taken into account when making decisions regarding interventions such as vaccination programmes.
ACKNOWLEDGEMENTS
We thank Calvin Cheng, Daniel Chu, Winnie Lim, Edward Ma, Hau Chi So and Jessica Wong for research support. This project was supported by the Harvard Center for Communicable Disease Dynamics from the National Institute of General Medical Sciences (grant no. U54 GM088558), the Research Fund for the Control of Infectious Disease, Food and Health Bureau, Government of the Hong Kong SAR (grant no. CHP-CE-03), and the Area of Excellence Scheme of the Hong Kong University Grants Committee (grant no. AoE/M-12/06). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
DECLARATION OF INTEREST
D.K.M.I. has received research funding from F. Hoffman-La Roche Ltd. J.S.M.P. receives research funding from Crucell NV and serves as an ad hoc consultant for GlaxoSmithKline and Sanofi. B.J.C. has received research funding from MedImmune Inc., and consults for Crucell NV.










