Article contents
On the selection of subaction and measure for a subclass of potentials defined by P. Walters
Published online by Cambridge University Press: 04 July 2012
Abstract
Suppose 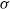 $\sigma $ is the shift acting on Bernoulli space
$\sigma $ is the shift acting on Bernoulli space 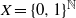 $X=\{0,1\}^{\mathbb {N}}$, and consider a fixed function
$X=\{0,1\}^{\mathbb {N}}$, and consider a fixed function 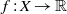 $f:X \to \mathbb {R}$ satisfying the Walters conditions (defined in [P. Walters. A natural space of functions for the Ruelle operator theorem. Ergod. Th. & Dynam. Sys.27 (2007), 1323–1348]). For each real value
$f:X \to \mathbb {R}$ satisfying the Walters conditions (defined in [P. Walters. A natural space of functions for the Ruelle operator theorem. Ergod. Th. & Dynam. Sys.27 (2007), 1323–1348]). For each real value 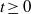 $t\geq 0$ we consider the Ruelle operator
$t\geq 0$ we consider the Ruelle operator 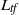 $L_{\mathit {tf}}$. We are interested in the main eigenfunction
$L_{\mathit {tf}}$. We are interested in the main eigenfunction 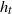 $h_t$ of
$h_t$ of 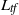 $L_{\mathit {tf}}$ and the main eigenmeasure
$L_{\mathit {tf}}$ and the main eigenmeasure 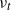 $\nu _t$ for the dual operator
$\nu _t$ for the dual operator 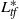 $L_{\mathit {tf}}^*$, which we consider normalized in such a way that
$L_{\mathit {tf}}^*$, which we consider normalized in such a way that 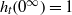 $h_t(0^\infty )=1$ and
$h_t(0^\infty )=1$ and 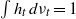 $\int h_t \,d\nu _t=1$ for all
$\int h_t \,d\nu _t=1$ for all 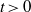 $t\gt 0$. We denote by
$t\gt 0$. We denote by 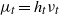 $\mu _t= h_t \nu _t$ the Gibbs state for the potential
$\mu _t= h_t \nu _t$ the Gibbs state for the potential 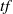 $\mathit {tf}$. By the selection of a subaction
$\mathit {tf}$. By the selection of a subaction 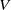 $V$, when the temperature goes to zero (or
$V$, when the temperature goes to zero (or 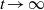 $t\to \infty $), we mean the existence of the limit
$t\to \infty $), we mean the existence of the limit 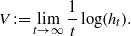 \[ V:=\lim _{t\to \infty }\frac {1}{t}\log (h_{t}). \]
\[ V:=\lim _{t\to \infty }\frac {1}{t}\log (h_{t}). \]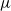 $\mu $, when the temperature goes to zero (or
$\mu $, when the temperature goes to zero (or 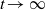 $t\to \infty $), we mean the existence of the limit (in the weak* sense)
$t\to \infty $), we mean the existence of the limit (in the weak* sense) 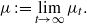 \[\mu :=\lim _{t\to \infty } \mu _t.\]
\[\mu :=\lim _{t\to \infty } \mu _t.\]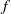 $f$ where the selection of a measure exists. These
$f$ where the selection of a measure exists. These 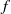 $f$ belong to a sub-class of potentials introduced by Walters. In this case, explicit expressions for the selected
$f$ belong to a sub-class of potentials introduced by Walters. In this case, explicit expressions for the selected 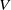 $V$can be obtained for a certain large family of parameters.
$V$can be obtained for a certain large family of parameters.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © 2012 Cambridge University Press
References
- 13
- Cited by

