Hostname: page-component-66644f4456-swwnq Total loading time: 0 Render date: 2025-02-12T18:07:09.852Z Has data issue: true hasContentIssue false
  • English
  • Français

Pointwise ergodic theorems beyond amenable groups

Published online by Cambridge University Press:  16 April 2012

LEWIS BOWEN  and
AMOS NEVO
LEWIS BOWEN
Affiliation:
Texas A&M University, College Station, TX, USA (email: lpbowen@math.tamu.edu)
AMOS NEVO
Affiliation:
Technion, Haifa, Israel (email: anevo@techunix.technion.ac.il)
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove pointwise and maximal ergodic theorems for probability-measure-preserving (PMP) actions of any countable group, provided it admits an essentially free, weakly mixing amenable action of stable type III$_1$. We show that this class contains all irreducible lattices in connected semi-simple Lie groups without compact factors. We also establish similar results when the stable type is III$_\lambda $, 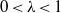$0 \lt \lambda \lt 1$, under a suitable hypothesis. Our approach is based on the following two principles. First, we show that it is possible to generalize the ergodic theory of PMP actions of amenable groups to include PMP amenable equivalence relations. Secondly, we show that it is possible to reduce the proof of ergodic theorems for PMP actions of a general group to the proof of ergodic theorems in an associated PMP amenable equivalence relation, provided the group admits an amenable action with the properties stated above.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 33 , Issue 3 , June 2013 , pp. 777 - 820
Copyright
Copyright © 2012 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[Aa97]Aaronson, J.. An Introduction to Infinite Ergodic Theory (Mathematical Surveys and Monographs, 50). American Mathematical Society, Providence, RI, 1997.Google Scholar
[AL05]Aaronson, J. and Lemańczyk, M.. Exactness of Rokhlin endomorphisms and weak mixing of Poisson boundaries. Algebraic and Topological Dynamics (Contemporary Mathematics, 385). American Mathematical Society, Providence, RI, 2005, pp. 77–87.Google Scholar
[AK63]Arnold, V. I. and Krylov, A. L.. Uniform distribution of points on a sphere and some ergodic properties of solutions of linear ordinary differential equations in the complex plane. Sov. Math. Dokl. 4 (1962), 1–5.Google Scholar
[As03]Assani, I.. Wiener–Wintner Ergodic Theorems. World Scientific Publishing Co., Inc., River Edge, NJ, 2003.Google Scholar
[Be71]Bewley, T.. Extension of the Birkhoff and von Neumann ergodic theorems to semigroup actions. Ann. Inst. Henri Poincaré VII (1971), 283–291.Google Scholar
[Bi31]Birkhoff, G. D.. Proof of the ergodic theorem. Proc. Natl. Acad. Sci. USA. 17 (1931), 656–660.CrossRefGoogle ScholarPubMed
[Bo08]Bowen, L.. Invariant measures on the space of horofunctions of a word-hyperbolic group. Ergod. Th. & Dynam. Sys. 30 (2010), 97–129.Google Scholar
[BN1]Bowen, L. and Nevo, A.. Geometric covering arguments and ergodic theorems for free groups. arXiv:0912.4953.Google Scholar
[BN2]Bowen, L. and Nevo, A.. von-Neumann and Birkhoff ergodic theorems for Gromov-hyperbolic groups. Preprint.Google Scholar
[BH99]Bridson, M. and Haefliger, A.. Metric spaces of non-positive curvature. Grundlehren der Mathematischen Wissenschaften (Fundamental Principles of Mathematical Sciences, 319). Springer, Berlin, 1999.Google Scholar
[Bu00]Bufetov, A. I.. Convergence of spherical averages for actions of free groups. Ann. of Math. (2) 155(3) (2002), 929–944.Google Scholar
[BKK11]Bufetov, A. I., Khristoforov, M. and Klimenko, A.. Cesaro convergence of spherical averages for measure-preserving actions of Markov semigroups and groups. arXiv:1101.5459.Google Scholar
[BS10]Bufetov, A. I. and Series, C.. A pointwise ergodic theorem for Fuchsian groups. arXiv Math. 1010.3362.Google Scholar
[Ca53]Calderon, A. P.. A general ergodic theorem. Ann. of Math. (2) 58 (1953), 182–191.Google Scholar
[Ch70]Chatard, J.. Applications des propriétés de moyenne d’un groupe localement compact à la théorie ergodique. Ann. Inst. Henri Poincaré VI (1970), 307–326.Google Scholar
[CFW81]Connes, A., Feldman, J. and Weiss, B. An amenable equivalence relation is generated by a single transformation. Ergod. Th. & Dynam. Sys. 1 (1981), 431–450.Google Scholar
[Dy59]Dye, H. A.. On groups of measure preserving transformation. I. Amer. J. Math. 81 (1959), 119–159.Google Scholar
[Dy63]Dye, H. A.. On groups of measure preserving transformations. II. Amer. J. Math. 85 (1963), 551–576.Google Scholar
[Em74]Emerson, W. R.. The pointwise ergodic theorem for amenable groups. Amer. J. Math. 96 (1974), 472–487.CrossRefGoogle Scholar
[FM77]Feldman, J. and Moore, C. C.. Ergodic equivalence relations and von Neumann algebras I. Trans. Amer. Math. Soc. 234 (1977), 289–324.CrossRefGoogle Scholar
[FN98]Fujiwara, K. and Nevo, A.. Maximal and pointwise ergodic theorems for word-hyperbolic groups. Ergod. Th. & Dynam. Sys. 18(4) (1998), 843–858.Google Scholar
[GN10]Gorodnik, A. and Nevo, A.. The Ergodic Theory of Lattice Subgroups (Annals of Mathematics Studies, 172). Princeton University Press, Princeton, NJ, 2010.Google Scholar
[GN11]Gorodnik, A. and Nevo, A.. Counting lattice points. J. Reine Angew. Math. (2011).Google Scholar
[GS00]Greschonig, G and Schmidt, K.. Ergodic decompositions of quasi-invariant probability measures. Colloq. Math. 84(2) (2000), 495–514.Google Scholar
[Gr99]Grigorchuk, R. I.. Ergodic theorems for the actions of a free group and a free semigroup. Mat. Zametki 65(5) (1999), 779–783 (Engl. Trans. Math. Notes 65 (1999)(5–6), 654–657).Google Scholar
[Gu68]Guivarc’h, Y.. Généralisation d’un théorème de von-Neumann. C. R. Acad. Sci. Paris 268 (1969), 1020–1023.Google Scholar
[INO08]Izumi, M., Neshveyev, S. and Okayasu, R.. The ratio set of the harmonic measure of a random walk on a hyperbolic group. Israel J. Math. 163 (2008), 285–316.CrossRefGoogle Scholar
[Ka97]Kaimanovich, V. A.. Amenability, hyperfiniteness and isoperimetric inequalities. C. R. Acad. Sci. Paris. Sér. I Math. 325(9) (1997), 999–1004.Google Scholar
[Ka03]Kaimanovich, V. A.. Double ergodicity of the Poisson boundary and applications to bounded cohomology. Geom. Funct. Anal. 13(4) (2003), 852–861.CrossRefGoogle Scholar
[Kr70]Krieger, W. A.. On the Araki–Woods Asymptotic Ratio set and Nonsingular Transformations (Lecture Notes in Mathematics, 160). Springer, Berlin and New York, 1970, pp. 158–177.Google Scholar
[Kr85]Krengel, U.. Ergodic Theorems (With a Supplement by Antoine Brunel. de Gruyter Studies in Mathematics, 6). Walter de Gruyter & Co., Berlin, 1985.Google Scholar
[KST99]Kechris, A. S., Solecki, S. and Todorcevic, S.. Borel chromatic numbers. Adv. Math. 141(1) (1999), 1–44.CrossRefGoogle Scholar
[KW91]Katznelson, Y. and Weiss, B.. The classification of nonsingular actions, revisited. Ergod. Th. & Dynam. Sys. 11(2) (1991), 333–348.CrossRefGoogle Scholar
[Li01]Lindenstrauss, E.. Pointwise theorems for amenable groups. Invent. Math. 146 (2001), 259–295.CrossRefGoogle Scholar
[Ma66]Mackey, G.. Ergodic theory and virtual groups. Math. Ann. 166 (1966), 187–207.Google Scholar
[Ma64]Maharam, D.. Incompressible transformations. Fund. Math. 56 (1964), 35–50.CrossRefGoogle Scholar
[MNS00]Margulis, G. A., Nevo, A. and Stein, E. M.. Analogs of Wiener’s ergodic theorems for semisimple Lie groups. II. Duke Math. J. 103(2) (2000), 233–259.CrossRefGoogle Scholar
[Mo66]Moore, C. C.. Ergodicity of flows in homogeneous spaces. Amer. J. Math. 88 (1966), 154–178.Google Scholar
[Mo08]Moore, C.. Virtual groups 45 years later. Group Representations, Ergodic Theory, and Mathematical Physics: a Tribute to George W. Mackey (Contemporary Mathematics, 449). American Mathematical Society, Providence, RI, 2008, pp. 263–300.CrossRefGoogle Scholar
[Ne94a]Nevo, A.. Harmonic analysis and pointwise ergodic theorems for non-commuting transformations. J. Amer. Math. Soc. 7 (1994), 875–902.CrossRefGoogle Scholar
[Ne94b]Nevo, A.. Pointwise ergodic theorems for radial averages on simple Lie groups. I. Duke Math. J. 76(1) (1994), 113–140.Google Scholar
[Ne97]Nevo, A.. Pointwise ergodic theorems for radial averages on simple Lie groups. II. Duke Math. J. 86(2) (1997), 239–259.Google Scholar
[Ne05]Nevo, A.. Pointwise ergodic theorems for actions of groups. Handbook of Dynamical Systems, vol. 1B. Eds. Hasselblatt, B. and Katok, A.. Elsevier, Amsterdam, 2006, pp. 871–982.Google Scholar
[NS94]Nevo, A. and Stein, E.. A generalization of Birkhoff’s pointwise ergodic theorem. Acta Math. 173(1) (1994), 135–154.Google Scholar
[NS97]Nevo, A. and Stein, E.. Analogs of Wiener’s ergodic theorems for semisimple groups. I. Ann. of Math. (2) 145(3) (1997), 565–595.Google Scholar
[Ok03]Okayasu, R.. Type III factors arising from Cuntz–Krieger algebras. Proc. Amer. Math. Soc. 131(7) (2003), 2145–2153.Google Scholar
[Os65]Oseledets, V. I.. Markov chains, skew-products, and ergodic theorems for general dynamical systems. Theory Probab. Appl. 10 (1965), 551–557.Google Scholar
[Pa76]Patterson, S. J.. The limit set of a Fuchsian group. Acta Math. 136 (1976), 241–273.Google Scholar
[Ro62]Rota, J. C.. An ‘Alternierende Verfahren’ for general positive operators. Bull. Amer. Math. Soc. (N.S.) 68 (1962), 95–102.Google Scholar
[RR97]Ramagge, J. and Robertson, G.. Factors from trees. Proc. Amer. Math. Soc. 125(7) (1997), 2051–2055.Google Scholar
[Sh88]Shulman, A.. Maximal ergodic theorems on groups. Dep. Lit. NIINTI, No. 2184, (1988).Google Scholar
[Sp87]Spatzier, R. J.. An example of an amenable action from geometry. Ergod. Th. & Dynam. Syst. 7(2) (1987), 289–293.Google Scholar
[Su78]Sullivan, D.. On the ergodic theory at infinity of an arbitrary discrete group of hyperbolic motions. Riemann Surfaces and Related Topics: Proceedings of the 1978 Stony Brook Conference (State Univ. New York, Stony Brook, N.Y., 1978) (Annals of Mathematics Studies, 97). Princeton University Press, Princeton, NJ, 1981, pp. 465–496.Google Scholar
[Su82]Sullivan, D.. Discrete conformal groups and measurable dynamics. Bull. Amer. Math. Soc. (N.S.) 6(1) (1982), 57–73.Google Scholar
[SW71]Stein, E. and Weiss, G.. Fourier Analysis on Euclidean spaces. Princeton University Press, Princeton, NJ, 1971.Google Scholar
[Te72]Tempelman, A.. Ergodic theorems for general dynamical systems. Trudy Moskov. Mat. 26 (1972), 95–132.Google Scholar
[Te92]Tempelman, A.. Ergodic theorems for group actions. Informational and Thermodynamical Aspects (Mathematics and its Applications, 78). Kluwer Academic Publishers Group, Dordrecht, 1992, Translated and Revised from the 1986 Russian Original. xviii+399 pp.Google Scholar
[Va63]Varadarajan, V. S.. Groups of automorphisms of Borel spaces. Trans. Amer. Math. Soc. 109 (1963), 191–220.Google Scholar
[vN32]von Neumann, J.. Proof of the Quasi-ergodic Hypothesis. Proc Natl. Acad. Sci. USA 18(1) (1932), 70–82.Google Scholar
[We03]Weiss, B.. Actions of amenable groups. Topics in Dynamics and Ergodic Theory (London Mathematical Society Lecture Note Series, 310). Cambridge University Press, Cambridge, 2003, pp. 226–262.Google Scholar
[Wi39]Wiener, N.. The ergodic theorem. Duke Math. J. 5 (1939), 1–18.Google Scholar
[Zi77]Zimmer, R.. Orbit spaces of unitary representations, ergodic theory and simple Lie groups. Ann. of Math. (2) 106 (1977), 573–588.CrossRefGoogle Scholar
[Zi78]Zimmer, R.. Amenable ergodic group actions and an application to Poisson boundaries of random walks. J. Funct. Anal. 27 (1978), 350–372.Google Scholar
[Zi84]Zimmer, R.. Ergodic Theory and Semisimple Groups. Birkhauser, Boston, 1984.Google Scholar