Article contents
Ruelle operator with weakly contractive iterated function systems
Published online by Cambridge University Press: 31 August 2012
Abstract
The Ruelle operator has been studied extensively both in dynamical systems and iterated function systems (IFSs). Given a weakly contractive IFS 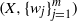 $(X, \{w_j\}_{j=1}^m)$ and an associated family of positive continuous potential functions
$(X, \{w_j\}_{j=1}^m)$ and an associated family of positive continuous potential functions 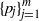 $\{p_j\}_{j=1}^m$, a triple system
$\{p_j\}_{j=1}^m$, a triple system 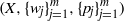 $(X, \{w_j\}_{j=1}^m, \{p_j\}_{j=1}^m)$is set up. In this paper we study Ruelle operators associated with the triple systems. The paper presents an easily verified condition. Under this condition, the Ruelle operator theorem holds provided that the potential functions are Dini continuous. Under the same condition, the Ruelle operator is quasi-compact, and the iterations sequence of the Ruelle operator converges with a specific geometric rate, if the potential functions are Lipschitz continuous.
$(X, \{w_j\}_{j=1}^m, \{p_j\}_{j=1}^m)$is set up. In this paper we study Ruelle operators associated with the triple systems. The paper presents an easily verified condition. Under this condition, the Ruelle operator theorem holds provided that the potential functions are Dini continuous. Under the same condition, the Ruelle operator is quasi-compact, and the iterations sequence of the Ruelle operator converges with a specific geometric rate, if the potential functions are Lipschitz continuous.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © 2012 Cambridge University Press
References
- 6
- Cited by

