Article contents
The attracting centre of a continuous self-map of the interval
Published online by Cambridge University Press: 19 September 2008
Abstract
Let ƒ denote a continuous map of a compact interval I to itself. A point x ∈ I is called a γ-limit point of ƒ if it is both an ω-limit point and an α-limit point of some point y ∈ I. Let Γ denote the set of γ-limit points. In the present paper, we show that (1)  −Γ is either empty or countably infinite, where
−Γ is either empty or countably infinite, where 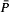 denotes the closure of the set P of periodic points, (2) x ∈ I is a γ-limit point if and only if there exist y1 and y2 in I such that x is an ω-limit point of y1, and y1 is an ω-limit point of y2, and if and only if there exists a sequence y1, y2,…of points in I such that x is an ω-limit point of y1, and yi is an ω-limit point of yi+1 for every i ≥ 1, and (3) the period of each periodic point of ƒ is a power of 2 if and only if every γ-limit point is recurrent.
denotes the closure of the set P of periodic points, (2) x ∈ I is a γ-limit point if and only if there exist y1 and y2 in I such that x is an ω-limit point of y1, and y1 is an ω-limit point of y2, and if and only if there exists a sequence y1, y2,…of points in I such that x is an ω-limit point of y1, and yi is an ω-limit point of yi+1 for every i ≥ 1, and (3) the period of each periodic point of ƒ is a power of 2 if and only if every γ-limit point is recurrent.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Cambridge University Press 1988
References
REFERENCES
- 11
- Cited by

