Density of mode-locking property for quasi-periodically forced Arnold circle maps

Abstract

We show that the mode-locking region of the family of quasi-periodically forced Arnold circle maps with a topologically generic forcing function is dense. This gives a rigorous verification of certain numerical observations in [M. Ding, C. Grebogi and E. Ott. Evolution of attractors in quasiperiodically forced systems: from quasiperiodic to strange nonchaotic to chaotic. Phys. Rev. A 39(5) (1989), 2593–2598] for such forcing functions. More generally, under some general conditions on the base map, we show the density of the mode-locking property among dynamically forced maps (defined in [Z. Zhang. On topological genericity of the mode-locking phenomenon. Math. Ann. 376 (2020), 707–72]) equipped with a topology that is much stronger than the 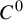$C^0$ topology, compatible with smooth fiber maps. For quasi-periodic base maps, our result generalizes the main results in [A. Avila, J. Bochi and D. Damanik. Cantor spectrum for Schrödinger operators with potentials arising from generalized skew-shifts. Duke Math. J. 146 (2009), 253–280], [J. Wang, Q. Zhou and T. Jäger. Genericity of mode-locking for quasiperiodically forced circle maps. Adv. Math. 348 (2019), 353–377] and Zhang (2020).

1. Introduction

Quasi-periodically forced maps (qpf-maps) are natural generalizations of Schrödinger cocycles, which played an important role in the recent study of a Schrödinger operator on ${\mathbb Z}$ with quasi-periodic potentials. The notion of uniform hyperbolicity naturally generalizes to the so-called mode-locking property of qpf-maps. Thus, the topological genericity of mode-locking among Schrödinger cocycles (for a given base map) would immediately imply that for topologically generic potential, the spectrum is a Cantor subset of ${\mathbb R}$ . We refer the readers to surveys [7, 17, 20] on more results on Schrödinger operators. It is natural to ask whether mode-locking holds generically among the set of general qpf-maps. The first result in this direction is provided by [21]. The authors showed that for a topologically generic frequency $\omega $ , the set of mode-locked qpf-maps with frequency $\omega $ is residual (with respect to the uniform topology). Their result is generalized in [22] to any fixed irrational frequency. In [22], the following natural generalization of the notion qpf-map is introduced (such consideration is not new, and has already appeared in [13, §5]).

Definition 1.1. (g-forced maps and rotation number)

Let $\mathrm {{Diff}}^{\,1}(\mathbb {T})$ , respectively $\mathrm {Homeo}(\mathbb {T})$ , denote the set of orientation preserving diffeomorphisms, respectively homeomorphisms, of $\mathbb {T}$ , and let $\mathrm {{Diff}}^1(\mathbb {R})$ , respectively $\mathrm {Homeo}(\mathbb {R})$ , denote the set of orientation preserving diffeomorphisms, respectively homeomorphisms, of $\mathbb {R}$ . We denote by $\pi _{{\mathbb R} \to {\mathbb T}}$ the canonical projection from ${\mathbb R}$ to $\mathbb {T} \simeq {\mathbb R}/{\mathbb Z}$ . We define $\mathrm {{Diff}}^{\,r}(\mathbb {T})$ , $\mathrm {{Diff}}^{\,r}(\mathbb {R})$ for $r \in {\mathbb Z}_{>1} \cup \{ \infty \}$ in a similar way.

Given a uniquely ergodic homeomorphism $g: X \to X$ , we say that $f: X \times \mathbb {T} \to X \times \mathbb {T}$ is a g-forced circle diffeomorphism, respectively g-forced circle homeomorphism, if there is a homeomorphism $F: X \times {\mathbb R} \to X \times {\mathbb R}$ of form

$$ \begin{align*} F(x, w) = (g(x), F_x(w))\quad \text{for all } (x, w) \in X \times {\mathbb R}, \end{align*} $$

where $F_x \in \mathrm {{Diff}}^1({\mathbb R})$ , respectively $\mathrm {Homeo({\mathbb R})}$ , for every $x \in X$ , such that $(\mathrm {Id} \times \pi _{{\mathbb R} \to \mathbb {T}}) \circ F = f \circ (\mathrm {Id} \times \pi _{{\mathbb R} \to \mathbb {T}})$ . In this case, we say that F is a lift of f.

For each lift F of a g-forced map f, the limit

$$ \begin{align*} \rho(F) = \lim_{n \to +\infty} \frac{\pi_{2} F^{n}(x, w)}{n} \end{align*} $$

exists, and is independent of $(x, w)$ (here $\pi _2$ is the canonical projection from $X \times {\mathbb R}$ to ${\mathbb R}$ , see [13, §5]). Moreover, the number $\rho (f) = \rho (F)\,\mod \!1$ is independent of the choice of the lift F.

Definition 1.2. (Mode-locking for g-forced maps)

Given a uniquely ergodic map $g: X \to X$ , we say that a g-forced circle homeomorphism f is mode-locked if $\rho (f') = \rho (f)$ for every g-forced circle homeomorphism $f'$ that is sufficiently close to f in the $C^0$ -topology. We denote the set of mode-locked g-forced circle homeomorphisms by $\mathcal {ML}$ .

The main result in [22] says that mode-locking is a topologically generic property among the set of g-forced circle homeomorphisms under a mild condition on g. Such a result generalizes the main results in [3, 21].

The current paper is a continuation of the above line of research.

It is natural to ask whether mode-locking could be generic among qpf-maps with higher regularity, with respect to the smooth topology. By the main result in [16], mode-locking can be rare in the measurable sense in many $C^1$ families. We hereby ask whether mode-locking could be generic in the topological sense.

Question 1.3. Is a $C^1$ generic quasi-periodically forced circle diffeomorphism mode- locked?

One can also ask for $C^r$ -genericity for any $r\geq 2$ . However, Question 1.3 already seems to be far from easy to answer. We also mention that a related question on qpf-circle maps has been asked in [11, Question 33], motivated by Eliasson’s theorem in [10]. Notice that a reducible qpf-circle map in [11] is accumulated by mode-locked qpf-maps.

This paper is an attempt to study Question 1.3. Although we could not give a direct answer to Question 1.3, we can show that mode-locking can be generic with respect to topologies which are much stronger than the $C^0$ topology. This is the content of our main theorem, Theorem 1.7. Thus, we provide some evidence to a positive answer to Question 1.3. It turns out that our theorem has implications for the quasi-periodically forced Arnold circle maps (see Theorem 1.11), a class of maps that were previously studied numerically by physicists (see [8]). We will elaborate on this point in §1.2.

1.1. Statements of the main results

Let X be a compact metric space. Let $g : X \rightarrow X$ be a strictly ergodic (that is, uniquely ergodic and minimal) homeomorphism with a non-periodic factor of finite-dimension, that is, there is a homeomorphism $\bar {g}:Y\rightarrow Y$ , where Y is an infinite compact subset of some Euclidean space $\mathbb {R}^d$ , and there is an onto continuous map $h: X \rightarrow Y$ such that $h \cdot g = \bar {g}\cdot h$ . We will show that for g satisfying some general condition, mode-locking is generic in topologies that are much stronger than the $C^0$ topology.

To state the condition we need, we introduce the following notion.

Definition 1.4. Let $g : X \rightarrow X$ be given as above, and let $\nu $ be the unique g-invariant measure. Let $G \subset \mathbb {R}$ be the subgroup of all t such that there exist continuous maps $\phi : X \rightarrow \mathbb {R}$ and $\psi : X \rightarrow \mathbb {R}/\mathbb {Z}$ with $t = \int \phi \,d\nu $ and $\psi (g(x)) - \psi (x) = \phi (x)\,\mod \!1$ . We call $G(g)$ the range of the Schwartzman asymptotic cycle for g.

Clearly, the problem about the density of mode-locking depends on the topology we choose to put on the space of maps. To treat the problem with respect to different topologies in a uniform fashion, we introduce the following definition.

Given $r \in {\mathbb Z}_{\geq 1}$ and $f, h \in \mathrm {{Diff}}^{\,r}({\mathbb T})$ , we set

$$ \begin{align*} d_{C^{r}({\mathbb T}, {\mathbb T})}(f, h) = \sum_{k = 0}^{r} \sup_{w \in {\mathbb T}} d(D^{k}f(w), D^{k}h(w)). \end{align*} $$

We define for any $r \in {\mathbb Z}_{\geq 1}$ that

$$ \begin{align*} d_{\mathrm{{Diff}}^{\,r}({\mathbb T})}(f, h) = d_{C^{r}({\mathbb T}, {\mathbb T})}(f, h) + d_{C^{r}({\mathbb T}, {\mathbb T})}(f^{-1}, h^{-1}). \end{align*} $$

We define

$$ \begin{align*} d_{\mathrm{{Diff}}^{\,\infty}({\mathbb T})}(f, h) = \sum_{k = 1}^{\infty} 2^{-k}\frac{d_{\mathrm{{Diff}}^{\,k}({\mathbb T})}(f, h)}{d_{\mathrm{{Diff}}^{\,k}({\mathbb T})}(f, h) + 1}. \end{align*} $$

Definition 1.5. Given a complete metric space ${{\mathcal {H}}}$ endowed with a complete metric $d_{ }$ , and a continuous map $\iota _{\mathcal {H}}: {{\mathcal {H}}} \to \mathrm {{Diff}}^1({\mathbb T})$ , by a slight abuse of notation, we denote $\iota _{\mathcal {H}} : {\mathcal {H}}^n \to \mathrm {{Diff}}^1({\mathbb T})$ by $\iota _{\mathcal {H}}((h_i)_{i=0}^{n - 1}) = \iota _{\mathcal {H}}(h_{n - 1}) \circ \cdots \circ \iota _{\mathcal {H}}(h_{0})$ for every integer $n \geq 1$ .

In the rest of the paper, we will only consider two classes of tuples $({\mathcal {H}}, d_{\mathcal {H}}, \iota _{\mathcal {H}})$ given below.

Example 1. Let $r \in {\mathbb Z}_{\geq 1} \cup \{ \infty \}$ . Let ${\mathcal {H}} = \widetilde{\mathrm{{Diff}}^{\,r}({\mathbb T})} = \{ f \in \mathrm {{Diff}}^{\,r}({\mathbb R}) \mid f(y + 1) = f(y) +1 \text { for all } y \in {\mathbb R} \}$ . We may define a distance $d_{\widetilde {\mathrm {{Diff}}^{\,r}({\mathbb T})}}$ on $\widetilde {\mathrm {{Diff}}^{\,r}({\mathbb T})}$ analogously to $d_{\mathrm {{Diff}}^{\,r}({\mathbb T})}$ . Let

$$ \begin{align*} d_{\mathcal{H}} = d_{\widetilde{\mathrm{{Diff}}^{\,r}({\mathbb T})}}. \end{align*} $$

We define $\iota _{\mathcal {H}}: {\mathcal {H}} \to \mathrm {{Diff}}^{\,1}({\mathbb T})$ by

$$ \begin{align*} \iota_{\mathcal{H}}(h)(y\,\mod \!1) = h(y)\,\mod \!1\quad \text{for all } y \in {\mathbb R}. \end{align*} $$

Example 2. Let ${\mathcal {H}} = {\mathbb R}$ . Let $P \in C^{\omega }({\mathbb T})$ be a non-constant real analytic function such that $\| P' \| < 1$ . We define $\iota _{\mathcal {H}}: {\mathcal {H}} \to \mathrm {{Diff}}^{1}({\mathbb T})$ by

$$ \begin{align*} \iota_{\mathcal{H}}(h)(w) = w + P(w) + h\,\mod \!1\quad \text{for all } w \in {\mathbb R}/{\mathbb Z}. \end{align*} $$

We let $d_{\mathcal {H}} = d_{{\mathbb R}}$ , where $d_{\mathbb R}$ denotes the Euclidean distance.

Remark 1.6. By definition, for $({\mathcal {H}}, d_{\mathcal {H}}, \iota _{\mathcal {H}})$ in either Example 1 or 2, we know that there exists some constant $C> 0$ such that for any $h_1, h_2 \in {{\mathcal {H}}}$ , we have

$$ \begin{align*}C d_{\mathcal{H}}(h_1, h_2) \geq d_{\mathrm{{Diff}}^{\,1}(\mathbb{T})}(\iota_{\mathcal{H}}(h_1), \iota_{\mathcal{H}}(h_2)).\end{align*} $$

As usual, let us denote by $C^0(X, {{\mathcal {H}}})$ the collection of continuous maps from X to ${{\mathcal {H}}}$ . We equip $C^0(X, {\mathcal {H}})$ with the norm

$$ \begin{align*} D_{\mathcal{H}}(H, H') = \sup_{x \in X}d_{\mathcal{H}}(H(x), H'(x)). \end{align*} $$

Given any $H \in C^{0}(X, {{\mathcal {H}}})$ and any $\epsilon> 0$ , we denote

$$ \begin{align*} \mathcal B_{\mathcal{H}}(H, \epsilon) = \{ H' \in C^{0}(X, {{\mathcal{H}}}) \mid D_{\mathcal{H}}(H, H') < \epsilon \}. \end{align*} $$

We denote by $\mathrm {{Diff}}^{\,0,1}_g(X \times \mathbb {T})$ the collection of g-forced circle diffeomorphisms of form

$$ \begin{align*} f: X \times \mathbb{T} &\to X \times \mathbb{T}, \\ (x, w) &\mapsto (g(x), f_x(w)), \end{align*} $$

where $f_x \in \mathrm {{Diff}}^{\,1}({\mathbb T})$ depends continuously on $x \in X$ . We denote

$$ \begin{align*} \|f\|_{C^{0,1}} &= \sup_{x \in X} (\|Df_x\|, \|D(f_x^{-1})\|) < \infty, \\ D_{C^{0,1}}(f, f') &= \sup_{x \in X} d_{\mathrm{{Diff}}^{\,1}({\mathbb T})}(f_x, (f')_x) < \infty. \end{align*} $$

By Remark 1.6, there is a continuous map ${\Phi } : C^0(X, {{\mathcal {H}}}) \to \mathrm {{Diff}}^{\,0,1}_g(X \times \mathbb {T})$ defined by

$$ \begin{align*} {\Phi} (H)(x, w) = (g(x), \iota_{\mathcal{H}}(H(x))(w)). \end{align*} $$

The main theorem of this paper is the following.

Theorem 1.7. Let $({{\mathcal {H}}}, d_{\mathcal {H}}, \iota _{\mathcal {H}})$ be given by Example 1 or 2. If $ G(g)$ is dense in $\mathbb {R}$ , then

(1.1) $$ \begin{align} \mathcal{ML}({\mathcal{H}}, \iota_{\mathcal{H}}) &:= \{ H \in C^0(X, {{\mathcal{H}}}) \mid {\Phi} (H) \in \mathcal{ML} \} \end{align} $$

is open and dense in $C^0(X, {{\mathcal {H}}})$ .

When $\iota _{\mathcal {H}}$ is clear from the context, we will abbreviate $\mathcal {ML}({\mathcal {H}}, \iota _{\mathcal {H}})$ as $\mathcal {ML}({\mathcal {H}})$ .

Instead of Example 2, it is more convenient to consider the following.

Example 3. Let P and $({\mathcal {H}}, d_{\mathcal {H}}, \iota _{\mathcal {H}})$ be as in Example 2. We assume in addition that P has no smaller period, that is, there exists no constant $\rho \in (0,1)$ such that $P(w + \rho ) \equiv P(w)$ .

We will actually give the proof for the following theorem, Theorem 1.8, since the discussions for Examples 1 and 3 can be organized in a unified way. In §6, we will prove Theorem 1.8 and deduce Theorem 1.7 as a corollary.

Theorem 1.8. Let $({{\mathcal {H}}}, d_{\mathcal {H}}, \iota _{\mathcal {H}})$ be given by Example 1 or 3. If $ G(g)$ is dense in $\mathbb {R}$ , then $\mathcal {ML}({\mathcal {H}}) = \mathcal {ML}({\mathcal {H}}, \iota _{\mathcal {H}}) $ is open and dense in $C^0(X, {{\mathcal {H}}})$ .

We note that $G(g)$ is dense for many interesting maps g, such as:

1. (1) minimal translations of $\mathbb {T}^d$ for any $d \geq 1$ ;

2. (2) the skew-shift $(x, y) \mapsto (x + \alpha , y + x)$ on $\mathbb {T}^2$ , where $\alpha $ is irrational;

3. (3) any strictly ergodic homeomorphism on a totally disconnected infinite compact subset of $\mathbb {R}^d$ for any $d\geq 1$ .

The proof of Theorem 1.7 is based on a description about the complement of $\overline {\mathcal {ML}({\mathcal {H}})}$ (see Theorem 1.10). Before stating the result, we introduce the following notions.

For a g-forced circle homeomorphism f with a lift F, for any integer $n \geq 1$ , we denote as in [22]

$$ \begin{align*}(f^n)_x := f_{g^{n-1}(x)} \circ \cdots \circ f_x, \quad (F^n)_x := F_{g^{n-1}(x)} \circ \cdots \circ F_x. \end{align*} $$

Definition 1.9. For any $f \in \mathrm {{Diff}}^{\,0,1}_g(X \times \mathbb {T})$ , the extremal fiberwise Lyapunov exponents of f, denoted by $L_{+}(f)$ and $L_{-}(f)$ , are given by formulas

$$ \begin{align*} \begin{aligned} &L_{+}(f) := \lim\limits_{n\rightarrow\infty} \frac{1}{n} \sup\limits_{(x ,w)\in X\times\mathbb{T}} \log D(f^n)_x(w),\\ &L_{-}(f) := \lim\limits_{n\rightarrow\infty} \frac{1}{n} \inf\limits_{(x ,w)\in X\times\mathbb{T}} \log D(f^n)_x(w). \end{aligned} \end{align*} $$

Let $({{\mathcal {H}}}, d_{\mathcal {H}}, \iota _{\mathcal {H}})$ be in Example 1 or 3. Then for any $H \in C^0(X, {{\mathcal {H}}})$ , we denote

$$ \begin{align*} L_{+}(H) = L_{+}(\Phi(H)), \quad L_{-}(H) = L_{-}(\Phi(H)). \end{align*} $$

Theorem 1.10. Let $({{\mathcal {H}}}, d_{\mathcal {H}}, \iota _{\mathcal {H}})$ be given by Example 1 or 3. Then either $\mathcal {ML}({\mathcal {H}})$ is dense in $C^0(X, {{\mathcal {H}}})$ , or there exists a residual subset $\mathcal A$ of $C^0(X, {{\mathcal {H}}}) \setminus \overline {\mathcal {ML}({\mathcal {H}})}$ such that ${\Phi } (H)$ has zero extremal fiberwise Lyapunov exponents for any $H \in \mathcal A$ . Here, the notion of a residual subset is defined with respect to the distance $D_{\mathcal {H}}$ on $C^0(X, {{\mathcal {H}}})$ .

Theorem 1.10 is similar to [3, Theorem 5], where the authors have shown that any cocycle in $C^{0}(X, { SL}(2, {\mathbb R}))$ that is not uniformly hyperbolic can be approximated by cocycles that are conjugate to elements in $C^{0}(X, {SO}(2, {\mathbb R}))$ . A similar approach is taken in [22] to prove the density with respect to the $C^0$ topology.

1.2. Application to quasi-periodically forced Arnold circle maps

A prominent example of a qpf-map is the so called ‘quasi-periodically forced Arnold circle map’,

$$ \begin{align*} f_{\alpha, \beta, \tau, q}: {\mathbb T}^2 \to {\mathbb T}^2, \quad (\theta,x) \mapsto \bigg(\theta+\omega, x + \tau + \frac{\alpha}{2\pi}\sin(2\pi x) + \beta q(\theta)\,\mod \!1\bigg), \end{align*} $$

with parameters $\alpha \in [0,1], \tau , \beta \in {\mathbb R}$ and a continuous forcing function $q : {\mathbb T} \to {\mathbb R}$ . It can be traced back to [12], and was then studied in [6, 8, 19], etc., as a simple model of an oscillator forced at two incommensurate frequencies. It has served as a source of motivation for a series of articles on this subject, such as [4, 14–16, 18, 22], etc.

Mode-locking was observed numerically on open regions in the $(\tau , \alpha )$ -parameter space, known as the Arnold tongues. An immediate question is whether for any given function $\beta q$ , mode-locking property holds for an open and dense set of $(\tau , \alpha )$ -parameters. There are numerical evidences to support such a conjecture. In [8, V. Conclusions], the authors wrote: ‘Various numerical experiments are performed to illustrate the different types of attractors that can arise in typical quasiperiodically forced systems. The central result is that in the two-dimensional parameter plane of K and V, the set of parameters, at which the system equations (2) and (3) exhibits strange nonchaotic attractors, has a Cantor-like structure, and is embedded between two critical curves.’ Notice that $(K, V)$ in [8] corresponds to $(\tau , \alpha )$ in our paper; and a parameter at which a strange non-chaotic attractor in [8] appears is in the complement of the mode-locking region. The following theorem gives a rigorous verification of the observation that the set of $(\tau , \alpha )$ where strange non-chaotic attractors appear contains no interior for a topologically generic forcing function.

Theorem 1.11. For any $\omega \in ({\mathbb R} \setminus {\mathbb Q})/{\mathbb Z}$ and any non-zero $\beta \in {\mathbb R}$ , there is a residual subset ${\mathcal U}_{\beta } \subset C^0({\mathbb T})$ such that for every $q \in {\mathcal U}_{\beta }$ , the set $\{ ( \tau , \alpha ) \mid f_{\alpha , \beta , \tau , q} \in \mathcal {ML} \}$ is an open and dense subset of ${\mathbb R} \times (0,1)$ .

Remark 1.12. We can clearly see from the proof below that a similar result holds when the function $\sin (2\pi x)$ is replaced by any non-constant real analytic function on ${\mathbb T}$ .

Proof. Fix some $\omega \in ({\mathbb R} \setminus {\mathbb Q})/{\mathbb Z}$ and define $g: {\mathbb T} \to {\mathbb T}$ by $g(x) = x + \omega $ . Fix some $\tau \in {\mathbb R}$ , $\alpha \in (0,1)$ , and $\beta \in {\mathbb R} \setminus \{0\}$ . We let ${{\mathcal {H}}}_{\alpha , \beta , \tau } = {\mathbb R}$ and let $d_{{\mathcal {H}}_{\alpha , \beta , \tau }}$ be the Euclidean metric. We take

$$ \begin{align*} \iota_{{\mathcal{H}}_{\alpha, \beta, \tau}}( h ) = \bigg(x \mapsto x + \tau + \frac{\alpha}{2\pi}\sin(2\pi x) + \beta h\,\mod \!1\bigg). \end{align*} $$

It is clear that $( {\mathcal {H}}_{\alpha , \beta , \tau }, d_{{\mathcal {H}}_{\alpha , \beta , \tau }}, \iota _{{\mathcal {H}}_{\alpha , \beta , \tau }})$ belongs to Example 2. Thus, we can apply Theorem 1.7 to deduce that: for every $\beta \in {\mathbb R} \setminus \{0\}$ , for every $\tau \in {\mathbb R}$ , $\alpha \in (0,1)$ , the set of $q \in C^0({\mathbb T})$ such that $f_{\alpha , \beta , \tau , q}$ is mode-locked, and is open and dense with respect to the uniform topology on $C^0({\mathbb T})$ . Then we take a dense subset $\{ (\tau _n, \alpha _n) \}_{n \geq 0}$ in ${\mathbb R} \times (0,1)$ , and for each $n \geq 0$ , we let $\mathcal B_n$ denote the set of $q \in C^0({\mathbb T})$ such that $f_{\alpha _n, \beta , \tau _n, q}$ is mode-locked. Then, $\mathcal B_n$ is open and dense for each $n \geq 0$ . Consequently, the set ${\mathcal U}_\beta = \bigcap _{n \geq 0} \mathcal B_n$ is a residual subset of $C^0({\mathbb T})$ , and for every $q \in {\mathcal U}_\beta $ , the open set $\{ ( \tau , \alpha ) \mid f_{\alpha , \beta , \tau , q} \in \mathcal {ML} \}$ is dense since it contains $(\tau _n, \alpha _n)$ for every $n \geq 0$ . This completes the proof.

1.3. Idea of the proof

The starting point for proving Theorem 1.7 is the following fact, which is already used in previous works such as [2, 22]: for a map that is not mode-locking, we can promote linear displacement for the orbit of a given point by arbitrarily small perturbation. The precise statements, summarized in §2.1, are quite general.

Compared with previous works, the challenge in our case here is that the perturbations of different points in a single fiber are strongly correlated; and moreover, we do not have a similar notion of the stable/unstable points on a fiber as for $SL(2, \mathbb {R})$ -cocycles. We overcome these difficulties by controlling the extremal Lyapunov exponents. Our proof consists of the two following main steps.

• • We first show that any map that cannot be approximated by mode-locking maps, can be perturbed to have zero extremal Lyapunov exponents. The precise statement is Theorem 1.10. This theorem is proved in §4 assuming Lemma 4.8, the key technical lemma of this paper.

  The key lemma Lemma 4.8 states the following: starting with some map F that is not mode-locking, either the extremal Lyapunov exponents both vanish or we can decrease their difference by a definite proportion (depending only on F) by arbitrary small perturbation. Although the general idea for proving Lemma 4.8 is originated from [1, 2, 5], the execution in our case is more complicated: unlike the case of $SL(2,\mathbb {R})$ -cocycles where the matching of (temporary) stable and unstable directions automatically reduces the growth of the derivative for every other point on that fiber, our general g-forced circle diffeomorphisms have no such convenient feature. We overcame this problem by carefully dividing a circle fiber into two parts so that for one part, we prove certain cancellation in the future, and for the other, in the past. For each part, the desired cancellation is also obtained for different reasons, under two distinct possibilities. This is done in §7.

• • After proving Theorem 1.10, we will use it as a starting point and perform a further perturbation to obtain the genericity of mode-locking. Since we may start with a map with vanishing extremal Lyapunov exponents, we may wish to perturb the map to create a closed strip that is mapped into its interior. In §5, we will describe the required perturbations made to a finite orbit. In §6, we will construct a global perturbation by combining several local perturbations at different scales. This is organized through the stratification introduced in [3], summarized in §3.1.

  For the above strategy to work, we need to use some features of maps in Examples 1 and 3 to ensure that ${{\mathcal {H}}}$ is sufficiently rich so that we can produce certain parabolic-like and hyperbolic-like circle diffeomorphisms by making perturbations in ${{\mathcal {H}}}$ (see Lemmata 4.3 and 7.3).

1.4. Notation

Given an integer $k \geq 1$ and $g_1,\ldots ,g_k \in \operatorname {\mathrm {Diff}}^{1}({\mathbb T})$ (or $\operatorname {\mathrm {Diff}}^1({\mathbb R})$ ), we denote by $\Pi _{i=1}^k g_i$ the map $g_k \circ \cdots \circ g_1$ .

Throughout this paper, in all the lemmata and propositions, we will assume that all the constants depend on some $({{\mathcal {H}}}, d_{\mathcal {H}}, \iota _{\mathcal {H}})$ fixed throughout this paper. For the sake of simplicity, we will not explicitly present such dependence.

2. Preliminary

We fix some $({{\mathcal {H}}}, d_{\mathcal {H}}, \iota _{\mathcal {H}})$ in Example 1 or 3 throughout this section. We let $g: X \to X$ be a map given at the beginning of §1.1.

2.1. Basic properties of dynamically forced maps

Let us recall some basic properties of g-forced circle homeomorphisms with a uniquely ergodic g, proved in [3, 22]. In particular, all the results in this subsection apply to maps in $ \mathrm {{Diff}}^{\,0,1}_g(X\times \mathbb {T})$ .

Let f be a g-forced circle homeomorphism with a lift F. Then for any g-forced circle homeomorphism $f'$ such that $D_{C^{0,1}}(f',f)<\tfrac 12$ , there exists a unique lift of $f'$ , denoted by $F'$ , such that $d_{\mathrm {{Diff}}^1({\mathbb R})}(F',F) < \tfrac 12$ . In the rest of this paper, we will say such $F'$ is the lift of f that is close to F.

We first notice the following alternative characterization of the mode-locking property (see [22, Definition 3 and Lemma 2]).

Lemma 2.1. A g-forced circle homeomorphism f is mode-locked if and only if there exists $\epsilon> 0$ such that we have

$$ \begin{align*} \rho(F_{-\epsilon}) = \rho(F) = \rho(F_{\epsilon}), \end{align*} $$

where F is an arbitrary lift of f, and $F_t(x, y) = F(x, y) + t$ for all $(x, y) \in X \times {\mathbb R}$ and $t \in {\mathbb R}$ .

Definition 2.2. For any $f \in \mathrm {{Diff}}^{\,0,1}_g(X \times \mathbb {T})$ , for any lift of f denoted by F, for any integer $n> 0$ , we set

$$ \begin{align*} \underline{M}(F, n) = \inf_{(x, y) \in X \times {\mathbb R}} ((F^n)_x(y) - y),\quad \overline{M}(F, n) = \sup_{(x, y) \in X \times {\mathbb R}}((F^n)_x(y) - y). \end{align*} $$

The following is [22, Lemma 3].

Lemma 2.3. Given some $f \in \mathrm {{Diff}}^{\,0,1}_g(X \times \mathbb {T})$ and a lift of f denoted by F, for any $\kappa _0> 0$ , there exists $N_0 = N_0(f, \kappa _0)> 0$ such that for any $n> N_0$ , we have $[\underline {M}(F, n), \overline {M}(F, n)] \subset n \rho (F) + (-n\kappa _0, n\kappa _0)$ .

The following is an immediate consequence of Lemma 2.3.

Corollary 2.4. Given some $f \in \mathrm {{Diff}}^{\,0,1}_g(X \times \mathbb {T})$ and a lift of f denoted by F, if for some $\epsilon> 0$ , we have $\rho (F_{-\epsilon }) < \rho (F)$ , respectively $\rho (F) < \rho (F_{\epsilon })$ , then there exist $\kappa _1 = \kappa _1(f, \epsilon )> 0$ and an integer $N_1 = N_1(f, \epsilon )> 0$ such that for any $n> N_1$ , we have

$$ \begin{align*} \overline{M}(F_{-\epsilon}, n) < \underline{M}(F, n) - n \kappa_1,\quad \mbox{respectively } \overline{M}(F, n) + n \kappa_1 < \underline{M}(F_\epsilon, n). \end{align*} $$

Given a g-forced circle homeomorphism f and a lift of f denoted by F, for any integer $N> 0$ , any $\kappa> 0$ , we define

(2.1) $$ \begin{align} \Omega_N(F, \kappa)=\{(x,y,z)\in X\times\mathbb{R}^2\mid |z- (F^N_x)(y)|< N \kappa \}. \end{align} $$

We recall the following result, which is analogous to [22, Lemma 8].

Lemma 2.5. Given $H \in C^0(X, \mathcal {H})$ , we let $f = \Phi (H)$ and let F be a lift of f. For any $\epsilon \in (0, 1/4)$ , there exists $\epsilon _0 = \epsilon _0(H, \epsilon ) \in (0, \epsilon )$ such that if we have $\rho (F_{\epsilon _0})> \rho (F) > \rho (F_{- \epsilon _0})$ , then by letting $\kappa _1 = \kappa _1(f, \epsilon _0)> 0$ and $N_1 = N_1(f, \epsilon _0)> 0$ be as in Corollary 2.4, the following is true. For any $\check {H} \in \mathcal B_{\mathcal {H}}(H, \epsilon _0)$ , for any integer $N \geq N_1$ , there exists a continuous map $\Phi ^{\check {H}}_N : \Omega _N(F, \kappa _1) \to \mathcal {H}^{N}$ such that for any $(x, y, z) \in \Omega _N(F, \kappa _1)$ , let $\Phi ^{\check {H}}_N(x, y, z) = (p_0,\ldots , p_{N-1})$ and let $\check {F}$ be the unique lift of $\Phi (\check {H})$ close to F (the map $\check {F}$ is well defined since $\epsilon _0 < \epsilon < 1/2$ ), then:

1. (1) $d_{\mathcal {H}}(p_i, \check {H}(g^{i}(x))) < 2\epsilon $ for every $0 \leq i \leq N-1$ ;

2. (2) let $P_i$ be the unique lift of $\iota _{\mathcal {H}}(p_i)$ close to $\check {F}_{g^{i}(x)}$ , then $P_{N-1} \cdots P_0(y) = z$ ;

3. (3) if $z = (\check {F}^{N})_{x}(y)$ , then $p_i = \check {H}(g^{i}(x))$ for every $0 \leq i \leq N-1$ .

Proof. The proof is almost identical to that of [22, Lemma 8]. We recall the proof for the convenience of the readers.

We notice that the following is clear for any $({\mathcal {H}}, d_{\mathcal {H}}, \iota _{\mathcal {H}})$ in Example 1 or 3: there is a continuous map $\varphi : {\mathcal {H}} \times (-1, 1) \to {\mathcal {H}}$ such that $\varphi (p, 0) = p$ , and for every $t \in (-1,1)$ , $P_t$ is a lift of $\iota _{\mathcal {H}}(\varphi (p, t))$ when P denotes a lift of $\iota _{\mathcal {H}}(p)$ . Let us denote $\check {H}_t(x) = \varphi (\check {H}(x) ,t)$ . We denote by $\check {F}_t$ the lift of $\check {H}_t$ for each $t \in (-1,1)$ . We assume that $\check {F}_t$ depends continuously on t. Then for any $x \in X$ and $y \in {\mathbb R}$ , the function $\epsilon ' \mapsto (\check {F}_{\epsilon '}^N)_{x}(y)$ is strictly increasing. By $d_{C^0}(\check {F}, F) \leq d_{\mathcal {H}}(\check {H}, H) < \epsilon _0$ , we have $(\check {F}_{2 \epsilon _0})_{x}(y) \geq (F_{\epsilon _0})_{x}(y)$ for any ${x \in X}$ and $y \in {\mathbb R}$ . Then by Lemma 2.4, we have $(\check {F}_{2\epsilon _0}^{N})_{x}(y) \geq (F_{\epsilon _0}^{N})_{x}(y)> (F^{N})_{x}(y) + N\kappa _1$ . Similarly, we have $(\check {F}^{N}_{-2\epsilon _0})_{\theta }(y) < (F^{N})_{\theta }(y) - N\kappa _1$ . Then, as in the proof of [22, Lemma 8], we see that the hypothesis of [22, Lemma 5] is satisfied. We can complete the proof by [22, Lemma 5] as in [22].

We have the following.

Proposition 2.6. (Tietze’s extension theorem for ${\mathcal {H}}$ )

Let $H \in C^0(X, {{\mathcal {H}}})$ and let Y be a compact subset of X. Given a constant $\epsilon> 0$ and a continuous map $H_0: Y \to {{\mathcal {H}}}$ such that for every $x \in Y$ , we have $d_{\mathcal {H}}(H(x), H_0(x)) < \epsilon $ , then there exists $H_1 \in \mathcal B_{\mathcal {H}}(H, \epsilon )$ such that $H_1(x) = H_0(x)$ for every $x \in Y$ .

Proof. If $({\mathcal {H}}, d_{\mathcal {H}}, \iota _{\mathcal {H}})$ is in Example 3, then this is the classical Tietze’s extension theorem. Now we assume that $({\mathcal {H}}, d_{\mathcal {H}}, \iota _{\mathcal {H}})$ is in Example 1. Notice that we can naturally identify $\widetilde {\mathrm {{Diff}}^r({\mathbb T})}$ with $\mathcal V_{r} = \{ \varphi \in C^r({\mathbb T}) \mid \varphi '(w)> - 1 \text { for all } w \in {\mathbb T} \}$ since we can associate to each $\varphi \in \mathcal V_r$ a mapping $y \mapsto y + \varphi (y\,\mod \!1)$ in $\widetilde {\mathrm {{Diff}}^r({\mathbb T})}$ and vice versa. Since $\mathcal V_r$ is a convex open subset of $C^r({\mathbb T})$ , which is a locally convex topological vector space, we can apply the generalization of Tietze’s extension theorem for such spaces in [9] to conclude the proof.

2.2. Lyapunov exponents

The following is an elementary yet useful observation.

Lemma 2.7. For any $f \in \mathrm {{Diff}}^{\,0,1}_g(X\times \mathbb {T})$ , we have $L_{+}(f)\geq 0\geq L_-(f)$ and $L_+(f), -L_-(f)\leq \log \Vert f \Vert _{C^{0,1}}$ .

Proof. Since for any $n \geq 1$ and any $x\in X$ , we have

(2.2) $$ \begin{align} \int_{\mathbb{T}} D(f^n)_x(w)\,dw = 1, \end{align} $$

we necessarily have that $L_-(f) \leq 0 \leq L_+(f)$ . By Definition 1.9 and the chain rule, we clearly have $\max (L_+(f),-L_-(f)) \leq \log \Vert f\Vert _{C^{0,1}}$ .

Given an integer $N> 0$ , we define for each $\mathbf {h} = (h_0, \ldots , h_{N-1}) \in {{\mathcal {H}}}^N$ that

$$ \begin{align*} \mathbf{L}_+(\mathbf{h}) &= \frac{1}{N} \sup\limits_{w \in {\mathbb T}} \log D(\iota_{\mathcal{H}}(h_{N-1}) \cdots \iota_{\mathcal{H}}(h_0))(w), \\ \mathbf{L}_-(\mathbf{h}) &= \frac{1}{N} \inf \limits_{w \in {\mathbb T}} \log D(\iota_{\mathcal{H}}(h_{N-1}) \cdots \iota_{\mathcal{H}}(h_0))(w). \end{align*} $$

Let $H \in C^0(X, {{\mathcal {H}}})$ . By definition, we have

$$ \begin{align*} L_{\pm}(H) = \lim_{n \to \infty} \mathbf{L}_{\pm}( (H(g^{i}(x)))_{i=0}^{n-1} ). \end{align*} $$

The following lemma, whose proof we omit, follows immediately from the subadditivity, e.g., $\log \| D(f_1 f_2) \| \leq \log \| D f_1 \| + \log \| D f_2 \|$ .

Lemma 2.8. Given $H \in C^0(X, {{\mathcal {H}}})$ , for any $\kappa _0> 0$ , there exists $N^{\prime }_0 = N^{\prime }_0(H, \kappa _0)> 0$ such that for any $n> N^{\prime }_0$ and any $x \in X$ , we have

$$ \begin{align*}[ \mathbf{L}_-( (H(g^{i}(x)))_{i=0}^{n-1} ), \mathbf{L}_+( (H(g^{i}(x)))_{i=0}^{n-1} ) ] \subset ( L_-( H ) - \kappa_0, L_+( H ) + \kappa_0). \end{align*} $$

3. A criterion from stratification

This section follows closely [3].

Let $g : X \rightarrow X$ be given at the beginning of §1.1. That is, X is a compact metric space and g is strictly ergodic with a non-periodic factor of finite dimension.

3.1. Dynamical stratification

As in [3], for any integers $n,N,d> 0$ , a compact subset $K \subset X$ is said to be:

1. (1) n-good if $g^{k}(K)$ for $0 \leq k \leq n-1$ are disjoint subsets;

2. (2) N-spanning if the union of $g^{k}(K)$ for $0 \leq k \leq N-1$ covers X;

3. (3) d-mild if for any $x \in X$ , $\{g^{k}(x) \mid k \in {\mathbb Z}\}$ enters $\partial K$ at most d times.

The following is an immediate consequence of [3, Lemmata 5.2–5.4].

Lemma 3.1. There exists an integer $d> 0$ such that for every integer $n> 0$ , for every open set $U \subset X$ , there exist an integer $D> 0$ and a compact subset $K \subset U$ that is n-good, D-spanning, and d-mild.

Let $K \subset X$ be an n-good, M-spanning, and d-mild compact subset. For each $x \in X$ , we set

$$ \begin{align*} l^{+}(x) &= \min\{j> 0 \mid g^{j}(x) \in \mathrm{int}(K)\}, \quad l^{-}(x) = \min\{j \geq 0 \mid g^{-j}(x) \in \mathrm{int}(K) \}, \\ l(x) &= \min\{j > 0 \mid g^{j}(x) \in K \}, \\ T(x) &= \{j \in {\mathbb Z} \mid - l^{-}(x) < j < l^{+}(x)\}, \quad T_B(x) = \{j \in T(x) \mid g^{j}(x) \in \partial K \}, \\ N(x) &= \#T_B(x), \quad K^{i} = \{x \in K \mid N(x) \geq d-i\}\quad \text{for all } -1 \leq i \leq d. \end{align*} $$

Let $Z^{i} = K^{i} \setminus K^{i-1} = \{x \in K \mid N(x) = d-i\}$ for each $0 \leq i \leq d$ .

Lemma 3.1 and the notation introduced above are minor modifications of those in the proof of [3, Lemma 4.1]. We also have the following (see [3] and also [22, Lemma 7]).

Lemma 3.2. We have:

1. (1) for any $x \in K$ , $l(x) \leq l^{+}(x)$ and $n \leq l(x) \leq D$ ;

2. (2) T and $T_B$ are upper-semicontinuous;

3. (3) T and $T_B$ , and hence also l, are locally constant on $Z^{i}$ ;

4. (4) $K^i$ is closed for all $-1 \leq i \leq d$ and $\emptyset = K^{-1} \subset K^{0} \subset \cdots \subset K^{d} = K$ ;

5. (5) for any $x \in K^{i}$ , any $0 \leq m < l^{+}(x)$ such that $g^{m}(x) \in K$ , we have $g^{m}(x) \in K^{i}$ .

3.2. A criterion for mode-locking

Given a g-forced circle homeomorphism f, a lift of f denoted by F, and a compact subset $K \subset X$ that is M-spanning for some $M> 0$ , let

$$ \begin{align*} f_K(x,w)& = f^{l(x)}(x,w)\quad \text{for all } (x,w) \in K \times \mathbb{T},\\ F_K(x,y)& = F^{l(x)}(x,y)\quad \text{for all } (x,y) \in K \times \mathbb{R}. \end{align*} $$

We have the following sufficient condition for mode-locking.

Lemma 3.3. If there exists an open set ${\mathcal R} \subset K\times \mathbb {T}$ (with respect to the induced topology on $K \times \mathbb {T}$ ) such that for each $x\in K$ , we have ${\mathcal R} \cap ( \{ x \}\times \mathbb {T})= \{ x \} \times I_x$ for some non-empty open interval $I_x \subsetneqq \mathbb {T}$ and $f_K(\overline {\mathcal {R}})\subset \mathcal {R}$ , then $f \in \mathcal {ML}$ .

Proof. Since K is M-spanning and $f_K(\overline {{\mathcal R}})\subset {\mathcal R}$ , there exists $\delta = \delta (f,M,\mathcal {R})> 0$ such that for any $\epsilon \in (-\delta , \delta )$ , we have $(f_\epsilon )_K(\overline {{\mathcal R}}) \subset \mathcal {R}$ . We inductively define a sequence of functions as follows:

$$ \begin{align*} l_n(x) = \begin{cases} l(x), & n=0, \\ l(g^{\Sigma^{n-1}_{j=0} l_j(x)}(x)), & n> 0. \end{cases} \end{align*} $$

Then it is direct to show, by an induction on n, that for any $x \in K$ , $y\in \mathbb {R}$ so that $(x,y \text {mod } 1)\in {\mathcal R}$ , we have

$$ \begin{align*} 1&> |\pi_2((F_\epsilon)_K)^n(x,y) - \pi_2(F_K)^n(x,y)|\\ & =|(F^{\Sigma^{n-1}_{i=0} l_i(x)}_\epsilon)_x(y) ) - (F^{\Sigma^{n-1}_{i=0} l_i(x)})_x(y)|\quad \text{for all } n\geq 0, \end{align*} $$

where $\pi _2: X \times \mathbb {R} \rightarrow \mathbb {R}$ is the canonical projection. This implies $\rho (F_\epsilon ) = \rho (F)$ for all $\epsilon \in (- \delta , \delta )$ and thus concludes the proof.

4. Density of zero Lyapunov exponent

The goal of this section is to prove Theorem 1.10. Throughout this section, we assume that $({\mathcal {H}}, d_{\mathcal {H}}, \iota _{\mathcal {H}})$ is in Example 1 or 3.

We first introduce the following notion.

Definition 4.1. We say that $H \in C^{0}(X, {{\mathcal {H}}})$ is contractible if:

1. (1) either $({\mathcal {H}}, d_{\mathcal {H}}, \iota _{\mathcal {H}})$ is in Example 1;

2. (2) or $({\mathcal {H}}, d_{\mathcal {H}}, \iota _{\mathcal {H}})$ is in Example 3, and there exists an integer $k> 1$ such that for any $x \in X$ and any $w \in {\mathbb T}$ , there exists $0 \leq i \leq k - 2$ such that $P"((f^{i + 1})_{x}(w)) \neq 0$ , where $f = \Phi (H)$ .

Lemma 4.2. The set of contractible $H \in C^{0}(X, {{\mathcal {H}}})$ is open and dense in $C^{0}(X, {{\mathcal {H}}})$ with respect to the metric $D_{\mathcal {H}}$ .

Proof. The openness is clear from the definition. To show the density, we will show that given any $H \in C^{0}(X, {{\mathcal {H}}})$ and an arbitrary $\epsilon> 0$ , we can construct some $H' \in C^{0}(X, {{\mathcal {H}}})$ such that $H'$ is contractible and $D_{\mathcal {H}}(H, H') < \epsilon $ .

If $({\mathcal {H}}, d_{\mathcal {H}}, \iota _{\mathcal {H}})$ is in Example 1, then it suffices to take $H' = H$ .

Now assume that $({\mathcal {H}}, d_{\mathcal {H}}, \iota _{\mathcal {H}})$ is in Example 3. Denote $A = \{ w \in {\mathbb T} \mid P"(w) = 0 \}$ . Since P is a non-constant analytic function, A is a finite set. For any $\epsilon> 0$ , there exists $\check {H} \in \mathcal B_{\mathcal {H}}(H, \epsilon )$ such that, by denoting $\check {f} = \Phi (\check {H})$ , we have $\check {f}_{x_0}(A) \cap A = \emptyset $ for some $x_0 \in X$ . By continuity, for every x sufficiently close to $x_0$ , we have $\check {f}_{x}(A) \cap A = \emptyset $ . We can then easily deduce that $\check {H}$ is contractible by the minimality of g.

The following lemma gives the key property of a contractible element that we will use. We will only need this lemma in §5, and the readers can skip it during the first reading and come back here later.

Lemma 4.3. If $H \in C^{0}(X, {{\mathcal {H}}})$ is contractible, then the following hold: there exist some $\epsilon> 0$ , an integer $k> 0$ , and a continuous map $E : [0, 1] \times {\mathbb T} \times X \times \mathcal B_{\mathcal {H}}(H, \epsilon ) \to {\mathcal {H}}^k$ such that if we denote $E(\sigma , w, x, \check {H} ) = ( h^{\sigma , w}_{i} )_{i=0}^{k-1}$ , then we have:

1. (1) $h^{0, w}_i = \check {H}(g^i(x))$ for every $w \in {\mathbb T}$ and every $0 \leq i \leq k-1$ ;

2. (2) $\iota _{\mathcal {H}}(( h^{\sigma , w}_{i} )_{i=0}^{k-1})(w) = \iota _{\mathcal {H}}(( \check {H}(g^i(x)) )_{i=0}^{k-1})(w)$ ;

3. (3) for every $\sigma _0 \in (0, 1)$ , there exist $r_0, \epsilon _2> 0$ such that

   $$ \begin{align*} D(\iota_{\mathcal{H}}(( h^{\sigma_0, w}_{i} )_{i=0}^{k-1}))(y) < e^{-\epsilon_2} D&(\iota_{\mathcal{H}}(( \check{H}(g^i(x)) )_{i=0}^{k-1}))(w), \quad y \in (w - r_0, w + r_0), \\\iota_{\mathcal{H}}(( h^{\sigma', w}_{i} )_{i=0}^{k-1})([w - r, w + r]) &\Subset \iota_{\mathcal{H}}(( h^{\sigma, w}_{i} )_{i=0}^{k-1})((w - r, w + r)), \\&\ \qquad\qquad\qquad\qquad 0 \leq \sigma < \sigma' \leq \sigma_0, 0 < r < r_0. \end{align*} $$

Proof. This lemma is clear if $({\mathcal {H}}, d_{\mathcal {H}}, \iota _{\mathcal {H}})$ is in Example 1, since we can make perturbations using the projective action on the circle by $SL(2, {\mathbb R})$ .

Now we assume that $({\mathcal {H}}, d_{\mathcal {H}}, \iota _{\mathcal {H}})$ is in Example 3. Let us denote $f = \Phi (H)$ , and let k be as in Definition 4.1.

Fix an arbitrary $x \in X$ . We define a function $c: X \times {\mathbb T} \times {\mathbb R} \to {\mathbb R}$ by

$$ \begin{align*} c(x, w, t) = P(w) + H(x) + t + P(w + P(w) + H(x) + t) + H(g(x)). \end{align*} $$

It is clear that c is continuous. By definition, we have

(4.1) $$ \begin{align} (f_{g(x)})_{-c(x, w, t) } \circ (f_x)_t(w) = w. \end{align} $$

By straightforward computation, given any $w_0 \in {\mathbb T}$ , we have

(4.2) $$ \begin{align} \partial_t \partial_w \{ ( f_{g(x)})_{-c(x, w_0, t)} \circ (f_x)_t(w) \}|_{t = 0, w = w_0} = P"( f_x(w_0) )( 1 + P'(w_0)) \neq 0 \end{align} $$

as long as $P"( f_x(w_0) ) \neq 0$ . In this case, the above term has the same sign as $P"( f_x(w_0) )$ .

By compactness and our hypothesis that H is contractible, there exists a finite open covering $\{ S_{\alpha } \times T_{\alpha } \}_{\alpha \in I}$ of $X \times {\mathbb T}$ , such that for each $\alpha \in I$ , there exists an integer ${0 \leq m_{\alpha } \leq k - 2}$ such that $P"( (f^{m_{\alpha } + 1})_{x}(w)) \neq 0$ for every $(x, w) \in S_{\alpha } \times T_{\alpha }$ . Since X is locally compact and Hausdorff, there exists a partition of unity $\{ \rho _{\alpha } \}_{\alpha \in I}$ subordinated to $\{ S_{\alpha } \times T_{\alpha } \}_{\alpha \in I}$ . Moreover, again by compactness and by equation (4.2), there exists some $\delta> 0$ such that

(4.3) $$ \begin{align} &\inf_{t \in (0, \delta]} \inf_{\alpha \in I} \inf_{(x, w_0) \in S_{\alpha} \times T_{\alpha}} t^{-1} | \partial_w \{ (f_{g(x)})_{-c(x, w_0, t)} \circ (f_x)_t(w) \}|_{ w = (f^{m_{\alpha}})_{x}(w_0)} | \nonumber \\ &\quad\geq \inf_{\alpha \in I} \inf_{(x, w_0) \in S_{\alpha} \times T_{\alpha}} | P"((f^{m_{\alpha} + 1})_{x}(w_0))(1 + P'((f^{m_{\alpha}})_{x}(w_0))) + o(1) |> 0. \end{align} $$

For any $0 \leq i \leq k -1$ , we denote

$$ \begin{align*} e_{k, i} = (\delta_{0, i}, \delta_{1, i}, \ldots, \delta_{k-1, i}) \in {\mathbb R}^{k}. \end{align*} $$

We define a map $Q: X \times {\mathbb T} \times [0,1] \to {\mathbb R}^{k}$ by

$$ \begin{align*} Q(x, w, t) = \sum_{\alpha \in I} \rho_{\alpha}(x, w) \mathrm{sgn}( P"((f^{m_{\alpha} + 1})_x(w)) )( \delta t e_{k, m_{\alpha}} - c(x, w, \delta t ) e_{k, m_{\alpha} + 1}). \end{align*} $$

We may define

$$ \begin{align*} E(\sigma, w, x, \check{H}) = (\check{H}(g^{i}(x)) )_{i=0}^{k - 1} - Q(x, w, \sigma). \end{align*} $$

We clearly have item (1). We can deduce item (2) from equation (4.1). We can deduce item (3) for $\check {H} = H$ by a straightforward computation using equations (4.2) and (4.3). Then we can verify item (3) for a general $\check {H} \in \mathcal B_{\mathcal {H}}(H, \epsilon )$ by continuity.

From the above proof, we also have the following result, which will be used in the proof of Lemma 7.3.

Lemma 4.4. Given an arbitrary $H \in C^0(X, {\mathcal {H}})$ , we denote $f = \Phi (H)$ . Then, for any $x \in X$ , $w_0, w_1 \in {\mathbb T}$ with $w_0 \neq w_1$ , for any $\epsilon> 0$ , there exists $(p_0, p_1) \in \mathcal B(H(x), \epsilon ) \times \mathcal B(H(g(x)), \epsilon )$ such that $\iota _{\mathcal {H}}(p_1) \iota _{\mathcal {H}}(p_0) (w_0) = (f^2)_x(w_0)$ and $\iota _{\mathcal {H}}(p_1) \iota _{\mathcal {H}}(p_0) (w_1) \neq (f^2)_x(w_1)$ .

Proof. The statement is clear if $({\mathcal {H}}, d_{\mathcal {H}}, \iota _{\mathcal {H}})$ is in Example 1.

Now we assume that $({\mathcal {H}}, d_{\mathcal {H}}, \iota _{\mathcal {H}})$ is in Example 3. Let t be a constant close to $0$ to be determined. We set

$$ \begin{align*} p_0 = H(x) + t,\quad p_1 = H(g(x)) - c(x, w_0, t). \end{align*} $$

Following the computations in Lemma 4.3, we see that

$$ \begin{align*} \iota_{\mathcal{H}}(p_1) \iota_{\mathcal{H}}(p_0) (w) &= w + P(w) + P( w + P(w) + H(x) + t)\\ &\quad - P(w_0) - P( w_0 + P(w_0) + H(x) + t). \end{align*} $$

Then it is clear that $\iota _{\mathcal {H}}(p_1) \iota _{\mathcal {H}}(p_0) (w_0) = w_0$ . Since $w_0 \neq w_1$ , we have $ w_1 + P(w_1) + H(x) \neq w_0 + P(w_0) + H(x)$ . Then since P has no smaller period, $\iota _{\mathcal {H}}(p_1) \iota _{\mathcal {H}}(p_0) (w_1)$ is a non-constant real analytic function of t. Hence, there exists t arbitrarily close to $0$ such that $\iota _{\mathcal {H}}(p_1) \iota _{\mathcal {H}}(p_0) (w_1) \neq w_1$ . This concludes the proof.

We first reduce Theorem 1.10 to the following proposition by a standard argument.

Proposition 4.5. For any contractible $H \in C^0(X, {\mathcal {H}}) \setminus \overline { \mathcal {ML}({\mathcal {H}}) }$ and any $\epsilon> 0$ , there exists a contractible $H' \in C^0(X, {\mathcal {H}}) \setminus \overline { \mathcal {ML}({\mathcal {H}}) } $ such that $D_{\mathcal {H}}(H, H') < \epsilon $ and $\vert L_+(H')\vert , \vert L_-( H' )\vert < \epsilon $ .

Remark 4.6. If $ C^0(X, {\mathcal {H}}) = \overline { \mathcal {ML}({\mathcal {H}}) }$ , then the condition of Proposition 4.5 is void. In this case, the conclusion of Theorem 1.10 is already satisfied.

We can easily deduce Theorem 1.10 from Proposition 4.5.

Proof of Theorem 1.10

Let us assume that $C^0(X, {\mathcal {H}}) \neq \overline {\mathcal {ML}({\mathcal {H}})}$ . For any $\epsilon> 0$ , we denote

$$ \begin{align*}\mathcal{U}_\epsilon := \{ H \in C^0(X, {\mathcal{H}}) \setminus \overline{ \mathcal{ML}({\mathcal{H}}) } \mid \vert L_+( H )\vert, \vert L_-(H)\vert<\epsilon\}.\end{align*} $$

Given an arbitrary $\epsilon> 0$ , by the upper-, respectively lower-, semicontinuity of $L_+$ , respectively $L_-$ , we see that $\mathcal {U}_\epsilon $ is open. By Proposition 4.5 and Lemma 4.2, $\mathcal {U}_\epsilon $ is dense. Then the set $\mathcal {U}_0 := \bigcap _{n\geq 1} \mathcal {U}_{{1}/{n}}$ is a residual subset of $C^0(X, {\mathcal {H}}) \setminus \overline {\mathcal {ML}({\mathcal {H}})}$ . By definition, every $H \in \mathcal {U}_0$ satisfies $L_+( H ) = L_- ( H ) = 0$ .

We will deduce Proposition 4.5 from the following slightly more technical proposition.

Proposition 4.7. For any contractible $H \in C^0(X, {\mathcal {H}}) \setminus \overline { \mathcal {ML}({\mathcal {H}}) }$ such that $L_+(H)>L_-(H)$ , for any $\epsilon> 0$ , there exists a contractible $H' \in C^0(X, {\mathcal {H}}) \setminus \overline { \mathcal {ML}({\mathcal {H}}) }$ such that $D_{\mathcal {H}}(H, H') < \epsilon $ and

$$ \begin{align*} \max(-L_-( H' ),\ \ \,\, L_+( H' )) < \max(-L_-( H ),\ \ \,\, L_+( H ))\bigg(1- 10^{- 6}\bigg(\frac{ L_+( H ) - L_-( H )}{ \log\Vert {\Phi} (H) \Vert_{C^{0,1}} + 3 }\bigg)^2\bigg). \end{align*} $$

Proof of Proposition 4.5 assuming Proposition 4.7

By Lemma 2.7, ${L_-( H ) \kern1.3pt{\leq}\kern1.3pt 0 \kern1.3pt{\leq}\kern1.3pt L_+( H )}$ . Without loss of generality, we can assume $L_+( H )-L_-( H ) \geq \epsilon $ , for otherwise, we can let $H' = H$ . Without loss of generality, let us assume that

$$ \begin{align*} \mathcal B_{\mathcal{H}}(H, 2\epsilon) \subset C^0(X, {\mathcal{H}}) \setminus \overline{ \mathcal{ML}({\mathcal{H}}) }. \end{align*} $$

Denote

$$ \begin{align*} L = \log (\Vert {\Phi} (H) \Vert_{C^{0,1}} + 1) + 3. \end{align*} $$

Define $H_0 = H$ . Assume that for some integer $n\geq 0$ , we have constructed some contractible $H_n \in C^0(X, {\mathcal {H}}) \setminus \overline { \mathcal {ML}({\mathcal {H}}) }$ so that $D_{\mathcal {H}}(H_n, H)\leq (2^{-1}- 2^{-n-1})\epsilon $ and $L_+( H_n ) - L_-( H_n ) \geq \epsilon $ . Without loss of generality, we may assume that $\epsilon $ is sufficiently small so that we have by Remark 1.6 that

$$ \begin{align*} \| \Phi(H_n) \|_{C^{0,1}} \leq \| \Phi(H) \|_{C^{0,1}} + C D_{\mathcal{H}}(H_n, H) \leq \| \Phi(H) \|_{C^{0,1}} + 1. \end{align*} $$

Then, by Proposition 4.7, we can find a contractible $H_{n+1}\in C^0(X, {\mathcal {H}}) \setminus \overline { \mathcal {ML}({\mathcal {H}}) }$ so that $D_{\mathcal {H}}(H_{n+1}, H_n)\leq 2^{-n-2}\epsilon $ and

$$ \begin{align*} \max(-L_-( H_{n+1}), L_+( H_{n+1})) < \max(-L_-( H_n), L_+( H_n))\bigg(1- 10^{-6}\bigg(\frac{\epsilon}{ L}\bigg)^2 \bigg).\end{align*} $$

Notice that we have $D_{\mathcal {H}}(H_{n+1}, H)\kern1.4pt{\leq}\kern1.4pt (2^{-1}\kern1.4pt{-}\kern1.4pt 2^{-n-1})\epsilon \kern1.4pt{+}\kern1.4pt 2^{-n-2}\epsilon \kern1.4pt{\leq}\kern1.4pt (2^{-1}\kern1.4pt{-}\kern1.4pt 2^{-n-2})\epsilon $ . Then for some integer $m> 0$ , we would have $D_{\mathcal {H}}(H_m, H) < \epsilon $ and ${L_+(H_m) - L_-(H_m) < \epsilon }$ . We let $H' = H_m$ and this concludes the proof.

The rest of this section is dedicated to the proof of Proposition 4.7.

We have the following important lemma.

Lemma 4.8. For any contractible $H \in C^0(X, {\mathcal {H}}) \setminus \overline { \mathcal {ML}({\mathcal {H}}) } $ such that $L_+( H )>L_-( H )$ , for any $\epsilon> 0$ , there exists $N_4 = N_4(H,\epsilon )> 0$ such that the following is true. For any $x\in X$ , any integer $N \geq N_4$ , there exists $(p_0,\ldots , p_{N-1})\in {\mathcal {H}}^N$ such that:

1. (1) $d_{\mathcal {H}}(p_i, H(g^i(x)))<\epsilon $ for every $0\leq i\leq N-1$ ;

2. (2) we have

   
   where
   (4.4)

   

The proof of Lemma 4.8 is technical and will be deferred to §7.

We are now ready to state the proof of Proposition 4.7.

Proof of Proposition 4.7

Let us fix some contractible $H \in C^0(X, {\mathcal {H}}) \setminus \overline { \mathcal {ML}({\mathcal {H}}) }$ such that $L_+( H )>L_-( H) $ .

By Lemma 2.8, we set

$$ \begin{align*} N^{\prime}_0 = N^{\prime}_0(H, 1), \end{align*} $$

then for any $x \in X$ , for any $n> N^{\prime }_0$ , we have that

$$ \begin{align*} \mathbf{L}_+( (H(g^{i}(x)))_{i=0}^{n-1} ) \leq L_+(H) + 1,\quad \mathbf{L}_-( (H(g^{i}(x)))_{i=0}^{n-1} ) \geq L_-(H) - 1. \end{align*} $$

We set

$$ \begin{align*} N_4 = N_4\big(H, \tfrac{1}{4}\epsilon\big), \end{align*} $$

where the function $N_4$ is given by Lemma 4.8. We fix an arbitrary integer

(4.5) $$ \begin{align} N> N_4 + N^{\prime}_0. \end{align} $$

Denote by $\nu $ the unique g-invariant measure. Under the hypothesis of g, we can choose a subset $B\subset X$ by [1, Lemma 6] such that the return time from B to itself via g equals to either N or $N + 1$ , and $\nu (\partial B) = 0$ . We fix such B from now on.

By reducing the size of $\epsilon $ if necessary, we may assume that for any $H' \in \mathcal B_{\mathcal {H}}(H, \epsilon )$ , we have, for $n \in \{ N, N+1 \}$ , that

(4.6) $$ \begin{align} \mathbf{L}_+( (H'(g^{i}(x)))_{i=0}^{n-1} ) \leq L_+(H) + 2,\quad \mathbf{L}_-( (H'(g^{i}(x)))_{i=0}^{n-1} ) \geq L_-(H) - 2. \end{align} $$

Let $\delta> 0$ be a small constant such that

$$ \begin{align*} \sup_{x\in X}\sup_{x'\in B(x,\delta), 0\leq i\leq N} d_{\mathcal{H}}(H(g^i(x')), H(g^i(x)) )<\tfrac{1}{2}\epsilon. \end{align*} $$

Cover the closure of B by open sets $W_1,\ldots ,W_{k_1}$ with diameters less than $\delta /2$ . By [1, Lemma 3], we can choose $W_i$ so that $\nu (\partial W_i) = 0$ for all $1\leq i \leq k_1$ . Let ${U_i = W_i \setminus \bigcup _{j<i} W_j}$ . After discarding those $U_k$ which are disjoint from B, and rearranging the indexes, we can assume that for some integer $k_0> 0$ , for each $1\leq k\leq k_0$ , $B\cap U_k\not =\emptyset $ ; and the union of $U_k$ over $1\leq k\leq k_0$ covers B.

By our choice, we have $B=B_N\cup B_{N+1}$ , where $B_l$ denotes the set of points in B whose first return time to B equals to l. Let

$$ \begin{align*} V_0 = \bigcup^{N+1}_{l=N}\bigcup^{l-1}_{i=0}\partial(B_l\cap U_i). \end{align*} $$

Then $\nu (V_0 )=0.$

Denote by $\Gamma $ the set of $(k,l)$ such that $1\leq k\leq k_0, l\in \{N,N+1\}$ and $B_l \cap U_k\not =\emptyset $ . For each $(k,l)\in \Gamma $ , we choose a point $w_{k,l}\in B_l\cap U_k \setminus V_0$ .

Fix an arbitrary $(k, l) \in \Gamma $ . Note that $l \geq N> N_4$ . By Lemma 4.8 for $(\epsilon /2, H, w_{k, l}, l)$ in place of $(\epsilon , H, x, N)$ , we obtain $\mathbf {p} = (p^{k,l}_{0},\ldots , p^{k,l}_{l-1})\in {\mathcal {H}}^l$ such that:

1. (1) we have $d_{\mathcal {H}}(p^{k,l}_{i},H(g^i(w_{k,l})))<\tfrac 12\epsilon $ for any $0\leq i\leq l-1$ ;

2. (2) we have

   (4.7)

   

Now let $\eta> 0$ be a sufficiently small constant to be determined later. By the unique ergodicity of g, there exist an open set $V\supset V_0 $ and an integer $n_0>0$ such that

(4.8) $$ \begin{align} \frac{1}{n}| \{ j\mid 0\leq j\leq n-1, g^j(x)\in V \} | < \frac{\eta}{N+1}\quad \text{for all } x \in X\quad \text{for all } n\geq n_0. \end{align} $$

Moreover, we can assume that $w_{k,l}\not \in V$ for any $(k, l) \in \Gamma $ .

We define a map $H' \in C^0(X, {{\mathcal {H}}})$ by using Proposition 2.6 so that $D_{\mathcal {H}}(H, H') < \epsilon $ , and for any $(k,l)\in \Gamma $ , any $0\leq i\leq l-1$ , we have $H'(g^i(x)) = p^{k,l}_{i}$ for all $x \in B_l\cap U_k \setminus V$ .

By letting $\eta> 0$ be sufficiently small depending only on $H, \epsilon $ (this can be realized by choosing V of sufficiently small measure, and by letting $n_0$ be sufficiently big), we can ensure by equations (4.6), (4.7), and (4.8) that

By a similar argument, we obtain an analogous bound for $ - L_-(H')$ . Consequently, we have

We see that $H'$ satisfies the conclusion of Proposition 4.7.

5. Negative Lyapunov exponent

In this section, we will show that starting from a contractible $H \in C^0(X, {\mathcal {H}}) \setminus \overline {\mathcal {ML}({\mathcal {H}})}$ with vanishing extremal Lyapunov exponents, we can perform an arbitrarily small perturbation to create an interval on any prescribed fiber to be mapped arbitrarily small by an iterate of $\Phi (H)$ . Moreover, such perturbation can be arranged to have continuous parameter dependence.

Recall that for a lift F of a g-forced circle homeomorphism f, for every integer $N> 0$ and every $\kappa> 0$ , we have defined $\Omega _N(F, \kappa )$ in equation (2.1).

Given a contractible $H \in C^0(X, {{\mathcal {H}}})$ , we let $\epsilon> 0$ be a sufficiently small constant, and we let the integer $k> 0$ and the continuous map $E : [0, 1] \times {\mathbb T} \times X \times \mathcal B_{\mathcal {H}}(H, \epsilon ) \to {\mathcal {H}}^k$ be given by Lemma 4.3.

Proposition 5.1. Given a contractible $H \in C^0(X, {\mathcal {H}}) \setminus \overline {\mathcal {ML}({\mathcal {H}})}$ such that $L_+(H) = L_-(H) = 0$ , and letting F be a lift of $\Phi (H)$ , for any $\epsilon> 0$ , there exist $\kappa _3 = \kappa _3(H,\epsilon )\in (0, \tfrac 12), N_5 = N_5(H,\epsilon )>0$ such that for any integer $N\geq N_5$ , there exists $r_3 = r_3(H, N, \epsilon )>0$ such that for any $\check {H} \in \mathcal B_{\mathcal {H}}(H, \kappa _3)$ , for any $\bar {r}\in (0,r_3)$ , there exists a continuous function $\Psi _N: \Omega _N(F,\kappa _3) \rightarrow {\mathcal {H}}^N$ such that the following is true. For any $(x, y, z) \in \Omega _N(F, \kappa _3)$ , let $\Psi _N(x, y, z) = (p_0, \ldots , p_{N-1})$ , and let $P_i$ be the unique lift of $\iota _{\mathcal {H}}(p_i)$ that is close to $F_{g^{i}(x)}$ , then we have:

1. (1) $d_{\mathcal {H}}(p_i,\check {H}(g^i(x)) ) < 2\epsilon $ for every $0\leq i\leq N-1$ ;

2. (2) $P_{N-1} \circ \cdots \circ P_0([y-\bar {r}, y+\bar {r}])\subset [z-({1}/{10})\bar {r}, z+({1}/{10})\bar {r}];$

3. (3) if $(\check {F}^{N-1})_{x}(y) = z$ and $(\check {F}^{N-1})_{x}([y-\bar {r}, y+\bar {r}])\subset [z- ({1}/{10})\bar {r}, z+ ({1}/{10})\bar {r}]$ , where $\check {F}$ is the unique lift of $\Phi (\check {H})$ that is close to F, then $p_i=\check {H}(g^i(x))$ for every $0\leq i\leq N-1$ .

Proof. Let us denote for simplicity $f = {\Phi } (H)$ and then F is a lift of f. Without loss of generality, we assume $\epsilon \in (0,1)$ is sufficiently small to apply Lemma 4.3.

We fix a small constant $\sigma _0 = \sigma _0(f, \epsilon )> 0$ such that for every $\check {H} \in \mathcal B_{\mathcal {H}}(H, \epsilon )$ , $x \in X$ , and $w \in {\mathbb T}$ , we have

(5.1) $$ \begin{align} E(\sigma_0, w, x, \check{H}) \in \prod_{i=0}^{k-1} \mathcal B_{\mathcal{H}}( \check{H}(g^{i}(x)), \epsilon), \end{align} $$

where the map E is given by Lemma 4.3. We let $r_0, \epsilon _2$ be given by Lemma 4.3(3) for $\sigma _0$ .

Since $L_+(f) = L_-(f) = 0$ , there exists $N' =N'(H,\epsilon )>0 $ such that

$$ \begin{align*} \sup_{x\in X, w \in \mathbb{T}} |\!\log D(f^n)_x(w)|< \frac{n\epsilon_2}{4k}\quad \text{for all } n>N'. \end{align*} $$

Then we choose $\kappa ' = \kappa '(H,\epsilon )> 0$ to be sufficiently small so that for any $H' \in \mathcal B_{\mathcal {H}}(H, \kappa ')$ , by denoting $f' = {\Phi } (H')$ , we have

(5.2) $$ \begin{align} \sup_{x\in X, w \in \mathbb{T}} |\!\log D(f')^n_x(w)|< \frac{n\epsilon_2}{2k}\quad \text{for all } n>N'. \end{align} $$

We let $\epsilon _0 = \epsilon _0(H, \epsilon ) \in (0, \epsilon )$ be given by Lemma 2.5. We let $\kappa " = \kappa _1(H,\epsilon _0)$ be given by Corollary 2.4. By Lemma 2.3, there exists some $N" = N"(H,\epsilon )> 0$ such that for any $n> N"$ , we have

(5.3) $$ \begin{align} \sup_{x\in X, y\in\mathbb{R}}|(F^n)_x(y)-y-n\rho(F)|< \frac{({1}/{60})\epsilon_2}{k( \log(\Vert f\Vert_{C^{0,1}}+1)+1) }n\kappa". \end{align} $$

We choose $\kappa "'> 0$ to be sufficiently small, depending only on $H, \kappa "$ and $\epsilon _2$ , so that for any $H' \in \mathcal B_{\mathcal {H}}(H, \kappa "')$ , for any $n> N"$ , we have

(5.4) $$ \begin{align} \sup_{x\in X, y\in\mathbb{R}}|(F')^n_x(y)- (F^n)_x(y) |< \frac{({1}/{20})\epsilon_2}{k(\log(\Vert f\Vert_{C^{0,1}}+1)+1)}n\kappa" , \end{align} $$

where $F'$ denotes the lift of $f' = {\Phi } (H')$ that is close to F.

We define

(5.5) $$ \begin{align} \kappa_3& = \frac{1}{2}\min\bigg(\epsilon_0, \kappa',\kappa"', \frac{({1}/{100})\epsilon_2}{k ( \log(\Vert f\Vert_{C^{0,1}}+1)+1 )}\kappa"\bigg), \end{align} $$

(5.6) $$ \begin{align} N_5 &= 2N' + 2N" + 100 \frac{k}{\epsilon_2}(\log(\Vert f\Vert_{C^{0,1}}+1) + 1)N_1(H,\epsilon_0) + 100 \frac{k}{\epsilon_2}. \end{align} $$

Let $N> N_5$ and $(x, y, z)\in \Omega _N(F, \kappa _3)$ . We define

(5.7) $$ \begin{align} \bar{N} &= \bigg\lceil \frac{1}{k}\bigg( 1 - \frac{\epsilon_2}{10 k (\log(\Vert f\Vert_{C^{0,1}} + 1))}\bigg)N \bigg\rceil, \end{align} $$

(5.8) $$ \begin{align} r_3 &= (\Vert f\Vert_{C^{0,1}}+1)^{-N} r_0. \end{align} $$

Let $\check {H}$ be as in the proposition and let $\check {F}$ be the unique lift of $\check {f} = {\Phi } (\check {H})$ that is close to F. For any $\sigma \in [0, \sigma _0]$ , we define

$$ \begin{align*} ( v^\sigma_{ik + j})_{j=0}^{k-1} = E( \sigma, ( \check{f}^{ik})_x(y\,\mod \!1), g^{ik}(x), \check{H} )\quad \text{for all } 0 \leq i \leq \bar{N}-1. \end{align*} $$

By Lemma 4.3(2), (3), and equation (5.1), for every $\sigma \in [0, \sigma _0]$ , we have that

(5.9) $$ \begin{align} d_{\mathcal{H}}(v^{\sigma}_l, \check{H}(g^{l}(x))) < \epsilon\quad \text{for all } 0 \leq l \leq \bar{N}k-1 \end{align} $$

and

(5.10) $$ \begin{align} V^\sigma_{ik-1}\cdots V^\sigma_0(y)= (\check{F}^{ik})_x(y)\quad \text{for all } 1\leq i\leq \bar{N}, \end{align} $$

where $V^\sigma _j$ is the unique lift of $\iota _{\mathcal {H}}(v^\sigma _j)$ that is close to $\check {F}_{g^j(x)}$ .

We have the following.

Claim 5.2. For any $0\leq i\leq \bar {N} - 1$ , we have

$$ \begin{align*} D(V^{\sigma_0}_{(i+1)k-1}\cdots V^{\sigma_0}_{ik})(y') &< e^{- \epsilon_2} D((\check{F}^k)_x)( (\check{F}^{ik})_x(y))\\ &\qquad\quad \text{for all } y' \in ( (\check{F}^{ik})_x(y) - r_0, (\check{F}^{ik})_x(y) + r_0), \end{align*} $$

and for any $r"\in (0, r_0 )$ and any $0\leq \sigma _1 <\sigma _2 \leq \sigma _0$ , we have

$$ \begin{align*} V^{\sigma_2}_{(i+1)k-1}\cdots V^{\sigma_2}_{ik}( (\check{F}^{ik})_x(y)+[-r",r"])\Subset V^{\sigma_1}_{(i+1)k-1}\cdots V^{\sigma_1}_{ik}( (\check{F}^{ik})_x(y)+(-r",r")). \end{align*} $$

In particular, for any $\bar {r}\in (0, r_3)$ , we have

$$ \begin{align*} &&V^{\sigma_2}_{\bar{N} k -1}\cdots V_0^{\sigma_2}([y-\bar{r},y+ \bar{r}]) \Subset V^{\sigma_1}_{\bar{N}k - 1}\cdots V_0^{\sigma_1}([y-\bar{r}, y+\bar{r}]). \nonumber \end{align*} $$

Proof. The inequality and the first inclusion follow immediately from Lemma 4.3(3). The last statement follows from equation (5.8) by repeatedly applying the first statement.

By equation (5.4), $(x, y, z)\in \Omega _N(F, \kappa _3)$ , and equation (5.5), we have

$$ \begin{align*} \begin{aligned} | (\check{F}^N)_x(y)-z| &\leq | ( F^N)_x(y)-z| + | (\check{F}^N)_x(y) - (F^N)_x(y)|\\ &\leq N\bigg( \kappa_3 + \frac{({1}/{20})\epsilon_2}{k (\log(\Vert f\Vert_{C^{0,1}}+1)+1)}\kappa"\bigg)<(N-\bar{N} k)\kappa". \end{aligned} \end{align*} $$

Hence, we have $(g^{\bar {N} k}(x), (\check {F}^{\bar {N} k})_x(y),z) \in \Omega _{N-\bar {N} k}(F, \kappa ")$ . Moreover, by equation (5.6) and $N>N_5$ , we have $N-\bar {N}k>N_1(f,\epsilon _0)$ . Then we can apply Lemma 2.5 to define

$$ \begin{align*} (u_{\bar{N} k },\ldots, u_{N-1}) = \Phi^{\check{H}}_{N-\bar{N} k}(g^{\bar{N} k}(x), (\check{F}^{\bar{N} k})_x(y),z).\end{align*} $$

We have

(5.11) $$ \begin{align} d_{\mathcal{H}}(u_i, \check{H}(g^i(x))) < 2\epsilon\quad \text{for all } \bar{N} k \leq i\leq N-1. \end{align} $$

For every $\bar {N} k \leq i\leq N-1$ , let us denote by $U_i$ the unique lift of $\iota _{\mathcal {H}}(u_i)$ that is close to $\check {F}_{g^{i}(x)}$ .

Claim 5.3. For any $\bar {r}\in (0, r_3]$ , we have

$$ \begin{align*} U_{N-1}\cdots U_{\bar{N} k}V^{\sigma_0}_{\bar{N} k - 1}\cdots V_0^{\sigma_0}([y-\bar{r},y+ \bar{r}])\subset [z-\tfrac{1}{10}\bar{r}, z+\tfrac{1}{10}\bar{r}]. \end{align*} $$

Proof. By equation (5.2) and $\kappa _3 < \kappa '$ , we see that

(5.12) $$ \begin{align} \sup_{x \in X, y \in {\mathbb R}} |\!\log D (\check{F}^n)_x(y)| < \frac{n\epsilon_2}{2k}\quad \text{for all } n> N'. \end{align} $$

By equation (5.8), $\bar r \leq r_3$ , equation (5.12), and by repeatedly applying Claim 5.2, we obtain

$$ \begin{align*} D(V^{\sigma_0}_{\bar{N} k -1}\cdots V_0^{\sigma_0})(y')< e^{-\bar{N}\epsilon_2/2}\quad \text{for all } y'\in (y-\bar{r}, y+\bar{r}). \end{align*} $$

Thus,

(5.13) $$ \begin{align} V^{\sigma_0}_{\bar{N}k -1}\cdots V_0^{\sigma_0}((y-\bar{r}, y+\bar{r}))\subset V^{\sigma_0}_{\bar{N}k -1}\cdots V_0^{\sigma_0}(y)+e^{-\bar{N} \epsilon_2/2}(-\bar{r},\bar{r}). \end{align} $$

By equations (5.6), (5.7), (5.11), and (5.13), we have

(5.14) $$ \begin{align} &U_{N-1}\cdots U_{\bar{N} k} V^{\sigma_0}_{\bar{N} k - 1}\cdots V_0^{\sigma_0}([y-\bar{r},y+\bar{r}]) \\\subset\ &z+(\Vert f\Vert_{C^{0,1}}+1)^{N-\bar{N}k}e^{-\bar{N}\epsilon_2/2}[-\bar{r},\bar{r}]\subset [z-\tfrac{1}{10}\bar{r}, z+\tfrac{1}{10}\bar{r}], \nonumber \end{align} $$

since we have

$$ \begin{align*} (N-\bar{N}k) \log (\Vert f\Vert_{C^{0,1}}+1) - \bar{N}\epsilon_2/2 \leq - \bar{N}\epsilon_2/4 \leq - \log 10.\\[-34pt] \end{align*} $$

Let $\bar {r}\in (0, r_3)$ be given by the proposition. We define

$$ \begin{align*}\sigma_1 \!=\! \inf\{\sigma\!\in\! [0,\sigma_0]\mid U_{N-1}\cdots U_{\bar{N} k } V^\sigma_{\bar{N} k -1} \cdots V^\sigma_0([y-\bar{r}, y+\bar{r}])\! \subset\! [z-\tfrac{1}{10}\bar{r}, z+\tfrac{1}{10}\bar{r}]\}.\end{align*} $$

By Claim 5.3, we see that $\sigma _1$ is well defined. By the last inclusion in Claim 5.2, $\sigma _1$ depends continuously on $(x, y, z)$ . Let us define

$$ \begin{align*} p_i = \begin{cases} v^{\sigma_1}_{i}, & 0 \leq i \leq \bar{N}k - 1, \\ u_i, & \bar{N} k \leq i \leq N-1. \end{cases} \end{align*} $$

Conclusions (1)–(3) then follow from the construction.

6. Density of mode-locking

In this section, we will first give the proof of Theorem 1.8, and then deduce Theorem 1.7 as a corollary.

Proof of Theorem 1.8

Given an arbitrary $H \in C^0(X, {\mathcal {H}})$ , we will show that H can be approximated by elements in $\mathcal {ML}({\mathcal {H}})$ .

Without loss of generality, we may assume that every element in a neighborhood of H in $C^0(X, {\mathcal {H}})$ is contractible, since by Lemma 4.2, every element of $C^0(X, {\mathcal {H}})$ is a limit of elements with this property.

By Theorem 1.10, either H is already in $\overline {\mathcal {ML}({\mathcal {H}})}$ , in which case there is nothing left to prove, or, up to replacing H by an arbitrarily close element, we may assume without loss of generality that H is contractible and $L_+( H )= L_-( H )=0$ . It remains to show that for any $\epsilon> 0$ , there exists $H' \in \mathcal {ML}({\mathcal {H}})$ such that $D_{\mathcal {H}}(H, H')<\epsilon $ . To simplify the notation, let us denote $f = {\Phi } (H)$ and let F denote a lift of f.

Let integer $d> 0$ be given by Lemma 3.1. Let $\kappa _3$ be given by Proposition 5.1. Without loss of generality, we may assume that $\kappa _3(f, \delta )$ is monotonically increasing in $\delta $ . We inductively define positive constants $0 < \epsilon _{-1} < \epsilon _{0} < \cdots < \epsilon _{d}$ by the following formula:

$$ \begin{align*} \epsilon_d{\kern-1pt}={\kern-1pt}\frac{\epsilon}{4(d+1)}, \ \epsilon_{d-k}=\min \bigg(\frac{1}{2}\epsilon_{d-k+1},\frac{1}{2(d+1)}\kappa_3(f,\epsilon_{d-k+1})\bigg)\quad\! \text{for all } 1{\kern-1pt}\leq{\kern-1pt} k{\kern-1pt}\leq{\kern-1pt} d{\kern-1pt}+{\kern-1pt}1. \end{align*} $$

Then we have

(6.1) $$ \begin{align} 2(\epsilon_0+\cdots+\epsilon_d)<\epsilon, \ 2(\epsilon_0+\cdots+\epsilon_k)< \kappa_3(f,\epsilon_{k+1})\quad \text{for all } 0\leq k\leq d-1. \end{align} $$

We set $\kappa ' = \inf _{1\leq i\leq d} \kappa _3(f, \epsilon _i)$ . Recall that by our hypothesis, g is uniquely ergodic. Let us denote by $\nu $ the unique g-invariant measure on X. By our hypothesis that $G(g)$ (see Definition 1.4) is dense in $\mathbb {R}$ , we can choose a constant

(6.2) $$ \begin{align} \rho'\in(\rho(F)-\tfrac{1}{4}\kappa',\quad \rho(F)+\tfrac{1}{4}\kappa')\cap G(g). \end{align} $$

By Definition 1.4, there exist continuous maps $\phi : X\rightarrow \mathbb {R}$ and $\psi : X \rightarrow \mathbb {R}/\mathbb {Z}$ so that $\rho ' = \int \phi \,d\nu $ and $\psi (g(x))-\psi (x)=\phi (x)\,\mod \!1.$

Since g is uniquely ergodic, we can choose $n_0 = n_0(f,\epsilon )> 0$ to be a large integer so that

(6.3) $$ \begin{align} n_0>N_5(H,\epsilon_i)\quad \text{for all } -1\leq i\leq d \quad (\mbox{see Proposition}\ {5.1}\ \mbox{for}\ N_5) \end{align} $$

and for any integer $n> n_0$ , we have

(6.4) $$ \begin{align} \sup\limits_{x\in X}\vert \Sigma^{n-1}_{i=0} \phi(g^i(x))-n\rho' \vert < \tfrac{1}{4}n\kappa', \ \sup\limits_{x\in X, y \in {\mathbb R}} \vert (F^{n})_{x}( y ) - y - n \rho(F) \vert < \tfrac{1}{4}n\kappa'. \end{align} $$

We choose an open set $U \subset X$ such that $\phi |_U$ admits a continuous lift $\hat {\psi }: U \rightarrow {\mathbb R}$ . Namely, $\hat {\psi }$ is continuous and $\psi (x) = \hat {\psi }(x)\,\mod \!1$ for any $x \in U$ .

By Lemma 3.1 and by enlarging $n_0$ if necessary, we can choose a compact set $K \subset U$ that is d-mild, $n_0$ -good, and M-spanning for some $M> 0$ .

We choose an arbitrary $\bar {r}\in (0, \tfrac 14)$ such that

(6.5) $$ \begin{align} \bar{r}<r_3(H,l, \epsilon)\quad \text{for all } n_0< l\leq M, \end{align} $$

where $r_3$ is given by Proposition 5.1.

Let $\{ K^i \}^d_{i=-1}, \{Z^i \}^d_{i=0}$ and $l: X \to {\mathbb Z}_+$ be defined as in §3, associated to K. We will define a sequence of $H^{(i)} \in C^0(X, {\mathcal {H}}), 1 \leq i\leq d $ by induction.

We define $H^{(-1)} = H$ , $f^{(-1)} = f = {\Phi } (H^{(-1)})$ , and $F^{(-1)} = F.$ Assume that we have defined $H^{(k)}$ for some $-1 \leq k \leq d-1$ such that, let $F^{(k)}$ be the lift of $f^{(k)} = {\Phi } (H^{(k)})$ that is close to $F^{(k-1)}$ if $k \geq 0$ , then:

1. (f1) $D_{\mathcal {H}}(H^{(k)}, H)\leq 2(\epsilon _0+\cdots +\epsilon _k);$

2. (f2) for any $x\in K^k$ , we have $((F^{(k)})^{l(x)})_x(\hat {\psi }(x))=\hat {\psi }(g^{l(x)}(x))+\Sigma _{j=0}^{l(x)-1}\phi (g^j(x));$

3. (f3) for any $x\ {\in}\ K^k$ , we have $((F^{(k)})^{l(x)})_x(\hat {\psi }(x)\ {+}\ [-\bar {r},\bar {r}])\ {\subset}\ \hat {\psi }(g^{l(x)}(x))\ {+} \Sigma _{j=0}^{l(x)-1} \phi (g^j(x))+[-({1}/{10})\bar {r}, ({1}/{10})\bar {r}].$

Note that the above properties are true for $k = -1$ simply because $K^{-1} = \emptyset $ by Lemma 3.2(4).

For each $-1\leq j\leq d$ , we let

$$ \begin{align*}W^j = \bigcup_{x\in K^j} \bigcup_{0\leq i < l(x)} \{g^i(x)\}.\end{align*} $$

Since $K^d = K$ is M-spanning, we have $W^d = X$ . Recall that we have the following lemma.

Lemma 6.1. [22, Lemma 10]

Given an integer $0 \leq j \leq d$ , let $\{ x_n \}_{n \geq 0 }$ be a sequence of points in $K^j$ converging to $x'$ , and let $ \{l_n \in [0, l(x_n)\}_{n \geq 0}$ be a sequence of integers converging to $l'$ . Then, after passing to a subsequence, we have exactly one of the following possibilities:

1. either (1) $x' \in Z^{j}$ and $0 \leq l' < l(x')$ ;

2. or (2) $x' \in K^{j-1}$ , and there exist a unique $x" \in K^{j-1}$ and a unique $0 \leq l" < l(x")$ such that $g^{l'}(x') = g^{l"}(x") \in W^{j-1}$ .

In particular, $W^j$ is closed.

By equation (6.1) and item $(f1)$ , we have $D_{\mathcal {H}}(H^{(k)}, H) < \kappa _3(f,\epsilon _{k+1})$ . By equations (6.3) and (6.5), we can apply Proposition 5.1 to $(\epsilon _{k+1}, l, H, H^{(k)},\bar {r})$ in place of $(\epsilon , N, H, \check {H}, \bar {r})$ to define $\Psi _l$ for all $n_0 <l\leq M$ .

We define a continuous map $\tilde {H} : W^{k+1} \to {\mathcal {H}}$ such that $\tilde {H}(x) = H^{(k)}(x)$ for every ${x \in W^k}$ in the following way. Let

(6.6) $$ \begin{align} \tilde{H}(x) = H^{(k)}(x)\quad \text{for all } x\in W^k. \end{align} $$

For any $x\in Z^{k+1}$ , we have $n_0 <l(x)\leq M$ . By equations (6.2) and (6.4), we have

$$ \begin{align*} & \vert \hat{\psi}(x) + \sum\limits_{i=0}^{l(x)-1} \phi(g^i(x)) - (F^{l(x)})_{x}( \hat{\psi}(x) ) \vert \\&\quad\leq \bigg\vert\! \sum\limits_{i=0}^{l(x)-1} \phi(g^i(x))-l(x)\rho(F)\bigg\vert + \vert (F^{l(x)})_{x}( \hat{\psi}(x) ) - \hat{\psi}(x) - l(x)\rho(F)\vert \\&\quad< 3 \times \frac{1}{4}l(x)\kappa' < l(x)\kappa_3(f,\epsilon_{k+1}). \end{align*} $$

Then we can define

(6.7) $$ \begin{align} (\tilde{H}(x), \ldots, \tilde{H}(g^{l(x)-1}(x))) =\Psi_{l(x)}(x,\hat\psi(x),\hat\psi(x)+\sum^{l(x)-1}_{i=0}\phi(g^i(x)) ). \end{align} $$

By Proposition 5.1(1), we have

(6.8) $$ \begin{align} d_{\mathcal{H}}(\tilde{H}(g^i(x)), H^{(k)}(g^i(x))) < 2\epsilon_{k+1}\quad \text{for all } x\in Z^{k+1}, 0\leq i< l(x). \end{align} $$

For $x \in K^{k+1}$ , for each $0 \leq i < l(x)$ , we let $\tilde {F}_{i}$ be the lift of $\iota _{\mathcal {H}}(\tilde {H}(g^{i}(x)))$ that is close to $F^{(k)}_{g^{i}(x)}$ . By items $(f2), (f3)$ for k, and by Proposition 5.1(2), for any $x\in K^{k+1} = K^{k} \cup Z^{k+1}$ , we have

$$ \begin{align*} \tilde{F}_{l(x)-1} \cdots \tilde{F}_{0}(\hat\psi(x)) &= \hat\psi(x) + \sum^{l(x)-1}_{i=0} \phi(g^i(x)),\\\tilde{F}_{l(x)-1} \cdots \tilde{F}_{0}([\hat\psi(x)-\bar{r}, \hat\psi(x)+\bar{r}]) &\subset \hat\psi(x) + \sum^{l(x)-1}_{i=0} \phi(g^i(x))+\bigg[-\frac{1}{10}\bar{r},\dfrac{1}{10}\bar{r}\bigg]. \end{align*} $$

We have the following.

Lemma 6.2. The map $\tilde {H}$ is continuous.

Proof. It is enough to show that for any $\{x_n\}, \{l_n\}, x', l'$ in Lemma 6.1 with $j = k + 1$ , we have

(6.9) $$ \begin{align} \tilde{H}(g^{l_n}(x_n)) \rightarrow \tilde{H}(g^{l'}(x')),\quad n\rightarrow \infty. \end{align} $$

We first assume that conclusion (1) in Lemma 6.1 is true, namely, $x'\in Z^{k+1}$ . Then equation (6.9) follows immediately from Lemma 3.2(3) and the continuity of $\Psi _{l(x')}$ .

Now assume that conclusion (2) in Lemma 6.1 is true, namely, $x'\in K^k$ . It is enough to prove equation (6.9) in the following two cases: (1) $x_n \in K^k$ for all n; (2) $x_n \in Z^{k+1}$ for all n. In the first case, we have $g^{l_n}(x_n) \in W^k$ for all $ n$ . By Lemma 6.1, we have ${g^{l'}(x')\in W^k}$ . Then equation (6.9) follows from equation (6.6) and the fact that $F^{(k)}$ is continuous.

Assume that the second case is true, namely, $x_n\in Z^{k+1}$ for all n. Moreover, after passing to a subsequence, we can assume that there exists $l_0$ such that $l(x_n) = l_0$ for all n. By equation (6.7), we have

$$ \begin{align*} \tilde{H}(g^{l'}(x_n)) = \mbox{the}\ l'\mbox{th coordinate of } \Psi_{l_0}(x_n). \end{align*} $$

Then by the continuity of $\Psi _{l_0}$ and the fact that $x_n\rightarrow x', l_n\rightarrow l'$ as n tends to infinity, we have that

$$ \begin{align*} \tilde{H}(g^{l_n}(x_n)) \rightarrow \mbox{the}\ l'\mbox{th coordinate of } \Psi_{l_0}(x'), n\rightarrow \infty. \end{align*} $$

It is then enough to show that the $l'$ th coordinate of $\Psi _{l_0}(x')$ equals $F^{(k)}_{g^{l'}(x')}$ . By Proposition 5.1(3), it is enough to verify that

(6.10) $$ \begin{align} (({F}^{(k)})^{l_0})_{x'}(\hat\psi(x')) &= \hat\psi(x') + \sum^{l_0-1}_{i=0} \phi(g^i(x')), \end{align} $$

(6.11) $$ \begin{align} ((\tilde{F}^{(k)})^{l_0})_{x'}(\hat\psi(x')+[-\bar{r},\bar{r}]) &\subset \hat\psi(x') + \sum^{l_0-1}_{i=0} \phi(g^i(x'))+\bigg[-\dfrac{1}{10}\bar{r},\dfrac{1}{10}\bar{r}\bigg]. \end{align} $$

These follow from items $(f2), (f3)$ , and Lemma 3.2(5).

By equation (6.8) and Proposition 2.6, we can choose $H^{(k+1)}\in C^0(X, {\mathcal {H}})$ so that $D_{\mathcal {H}} (H^{(k+1)}, H^{(k)}) < 2\epsilon _{k+1}$ and satisfies that $H^{(k+1)}(x) = \tilde {H}(x)$ for all $x\in W^{k+1}$ . It is straightforward to verify items $(f1)$ – $(f3)$ for $k + 1$ . This completes the induction.

We let $H' = H^{(d)}$ , $f' = \Phi (H')$ , and let $\mathcal {R}= \bigcup _{x\in K}\{x\}\times (\psi (x)-\bar {r}, \psi (x)+\bar {r})$ . By item $(f3)$ , we can see that $f^{\prime }_K(\overline {{\mathcal R}})\subset \mathcal {R}$ . By Lemma 3.3, $f'$ is mode-locked, and hence $H' \in \mathcal {ML}({\mathcal {H}})$ . This concludes the proof.

Proof of Theorem 1.7

By Theorem 1.8, it remains to consider the case where $({\mathcal {H}}, d_{\mathcal {H}}, \iota _{\mathcal {H}})$ is given by Example 2. In this case, ${\mathcal {H}} = {\mathbb R}$ and $d_{\mathcal {H}} = d_{{\mathbb R}}$ . Moreover, we may assume that the function P for defining $({\mathcal {H}}, d_{\mathcal {H}}, \iota _{\mathcal {H}})$ (see Example 3) has a smaller period, for otherwise, $({\mathcal {H}}, d_{\mathcal {H}}, \iota _{\mathcal {H}})$ is given by Example 3, and we could already conclude by Theorem 1.8.

Now let $R^{-1} \in (0, 1)$ be the smallest positive period of P, where $R \in {\mathbb Z}_{> 0}$ (such R exists since P is non-constant). Then there exists a non-constant real analytic function $P \in C^{\omega }({\mathbb T})$ with no smaller period such that $\tilde {P}(R w) = RP(w)$ for every $w \in {\mathbb T}$ . Notice that we have $\| \tilde P' \| = \| P' \| < 1$ . For each $h \in {\mathbb R}$ , we define

$$ \begin{align*} \tilde{\iota}_{\mathcal{H}}(h)(w) = w + \tilde P(w) + h. \end{align*} $$

Then we have

$$ \begin{align*} R \iota_{\mathcal{H}}(h)(w) = \tilde\iota_{\mathcal{H}}(Rh)(Rw). \end{align*} $$

We define a continuous map $\tilde \Phi : C^0(X, {\mathcal {H}}) \to \mathrm {{Diff}}^{\,0,1}_g(X \times {\mathbb T})$ by

$$ \begin{align*} \tilde\Phi(H)(x, w) = (g(x), \tilde\iota_{\mathcal{H}}( H(x))(w)). \end{align*} $$

By definition, it is straightforward to deduce the equation

$$ \begin{align*} \rho(\tilde\Phi(R \cdot H)) = R \rho (\Phi(H)) \in {\mathbb R}/{\mathbb Z}, \end{align*} $$

where $R \cdot H$ denotes the function $x \mapsto R H(x)$ in $C^0(X, {\mathcal {H}})$ . By Lemma 2.1, we see that $\tilde \Phi (R \cdot H) \in \mathcal {ML}$ if and only if $\Phi (H) \in \mathcal {ML}$ . By definition, $({\mathcal {H}}, d_{\mathcal {H}}, \tilde {\iota }_{\mathcal {H}})$ is given by Example 3. By Theorem 1.8, the set $\mathcal {ML}(H, \tilde \iota _{\mathcal {H}})$ is dense. Hence, $\mathcal {ML}(H, \iota _{\mathcal {H}})$ is also dense. This concludes the proof.

7. Proof of Lemma 4.8

Throughout this section, we always assume that $({\mathcal {H}}, d_{\mathcal {H}}, \iota _{\mathcal {H}})$ is given by either Example 1 or 3.

Without loss of generality, we may assume that

$$ \begin{align*} C^0(X, {\mathcal{H}}) \setminus \overline{ \mathcal{ML}({\mathcal{H}}) } \neq \emptyset, \end{align*} $$

for otherwise, there is nothing to prove. We fix some contractible $H \in C^0(X, {\mathcal {H}}) \setminus \overline { \mathcal {ML}({\mathcal {H}}) }$ such that $L_+(H)>L_-(H)$ and an arbitrary $\epsilon> 0$ . Recall that we will need to show that there exists $N_4> 0$ such that for any $x \in X$ , any integer $N \geq N_4$ , there exists $(p_0,\ldots , p_{N-1})\in {\mathcal {H}}^N$ such that: (1) $d_{\mathcal {H}}(p_i, H(g^i(x)))<\epsilon $ for every $0\leq i\leq N-1$ ; and (2) we have

where $\unicode{x3bb} _0$ is given in equation (4.4).

We denote $f = \Phi (H)$ and denote by F a lift of f.

We have the following result, making use of only the fact that $H \in C^0(X, {\mathcal {H}}) \setminus \overline { \mathcal {ML}({\mathcal {H}}) }$ .

Lemma 7.1. There exist a constant $\kappa = \kappa (H)> 0$ and functions $\Delta , K: {\mathbb R}_+ \to {\mathbb R}_+$ such that the following is true. For any $\epsilon> 0$ , $n> K(\epsilon )$ , $\tilde H \in \mathcal B_{\mathcal {H}}(H, \kappa )$ , and $x \in X$ , we have

$$ \begin{align*} \inf_{y \in {\mathbb R}} [(F_{\epsilon}^n)_x(y) - (F^n)_{x}(y)]> n \Delta(\epsilon), \end{align*} $$

where F is an arbitrary lift of $\Phi (H)$ (clearly the left-hand side above is independent of the choice of the lift).

Proof. Take a constant $\kappa> 0$ such that $\mathcal B_{\mathcal {H}}(H, 2 \kappa ) \subset C^0(X, {\mathcal {H}}) \setminus \overline { \mathcal {ML}({\mathcal {H}}) }$ .

Assume in contrast that the lemma is false. Then there exist some $\epsilon> 0$ , an increasing sequence $\{ n_k \}_{k \geq 1}$ , a sequence $\{ H_k \in \mathcal B_{\mathcal {H}}(H, \kappa ) \}_{k \geq 1}$ , a sequence $\{ x_k \in X \}_{k \geq 1}$ , and a sequence $\{ y_k \in [0,1) \}_{k \geq 1}$ such that

(7.1) $$ \begin{align} ((F^{(k)}_{\epsilon})^{n_{k}})_{x_k} (y_k) - ((F^{(k)})^{n_k})_{x_k}(y_k) \leq n_k/k, \end{align} $$

where $F^{(k)}$ is a lift of $\Phi (H_k)$ . We may assume without loss of generality that the set $\{ F^{(k)} \}_{k \geq 1}$ is bounded in $C^0({\mathbb R}, {\mathbb R})$ ; and $H_k$ converges to some $\check {H}$ . Then, after passing to a subsequence, we may assume that $F^{(k)}$ converges to a lift $\check {F}$ of $\Phi (\check {H})$ .

Fix an arbitrary integer $m> 0$ . By equation (7.1), for all sufficiently large integer $k> 0$ , there exists some $0 \leq l_k \leq n_k - m$ such that, for $u_k = g^{l_k}(x_k)$ and some $z_k \in [0,1)$ , we have

$$ \begin{align*} ((F^{(k)}_{\epsilon})^{m})_{u_k}(z_k) - ((F^{(k)})^{m})_{u_k}(z_k) \leq 2m/k. \end{align*} $$

By extracting a subsequence, we may assume that $u_k$ converges to some $u \in X$ , and $z_k$ converges to some $z \in [0,1]$ . Then we have

(7.2) $$ \begin{align} (\check{F}_{\epsilon}^m)_{u}(z) - (\check{F}^m)_{u}(z) = 0. \end{align} $$

By our choice of $\kappa $ , it is clear that $\check {H} \in C^0(X, {\mathcal {H}}) \setminus \overline { \mathcal {ML}({\mathcal {H}}) }$ . Thus, equation (7.2) contradicts Corollary 2.4 if m is sufficiently large. Consequently, the lemma must be true.

We have the following corollary.

Corollary 7.2. Let $\Delta , K$ be given as in Lemma 7.1. Then there exists a constant $\kappa> 0$ such that the following is true. For any $\epsilon> 0$ , $n> K(\epsilon )$ , $x \in X$ , and any $(H_{i})_{i=0}^{n-1} \in {\mathcal {H}}^{n}$ such that $d_{\mathcal {H}}(H_i, H(g^{i}(x))) < \kappa $ , we have

$$ \begin{align*} \inf_{y \in {\mathbb R}} [(F_{n-1})_{\epsilon} \circ \cdots \circ (F_{0})_{\epsilon}(y) - F_{n-1} \circ \cdots \circ F_{0}(y)]> n \Delta(\epsilon), \end{align*} $$

where $F_i$ is an arbitrary lift of $\iota _{\mathcal {H}}(H_i)$ for each $0 \leq i \leq n-1$ .

Proof. Given $x \in X$ and $n> K(\epsilon )$ , we have by Proposition 2.6 that there exists some $\tilde H \in \mathcal B_{\mathcal {H}}(H, \kappa )$ and $\tilde H(g^{i}(x)) = H_i$ for every $0 \leq i \leq n-1$ . Then we can immediately deduce the corollary by Lemma 7.1.

In the following lemma, we will construct perturbations that resemble the parabolic elements in $SL(2, \mathbb {R})$ . They are given by certain circle diffeomorphisms having a unique fixed point with multiplier $1$ . For this purpose, we will use the fact that $({\mathcal {H}}, d_{\mathcal {H}}, \iota _{\mathcal {H}})$ is given by either Example 1 or 3.

Lemma 7.3. For every $\epsilon> 0$ , there exist an integer $M = M(H, \epsilon )> 0$ and a function $\delta _{\epsilon , M}: {\mathbb R}_+ \to {\mathbb R}_+$ such that for any $x \in X$ and $y \in {\mathbb R}$ , there exists $( p^{(j)}_{i} )_{i = 0}^{M - 1} \in {{\mathcal {H}}}^{M}$ , $j \in \{ 0,1 \}$ such that $d_{\mathcal {H}}(p^{(j)}_i, H(g^{i}(x))) < \epsilon $ for $j \in \{0,1\}$ and $0 \leq i \leq M -1$ , and the following is true. Denote by $P^{(0)}_i$ and $P^{(1)}_i$ lifts of $\iota _{\mathcal {H}}(p^{(0)}_i)$ and $\iota _{\mathcal {H}}(p^{(1)}_i)$ , respectively, which are close to each other. Then we have:

1. (1) $P^{(1)}_{M -1} \circ \cdots \circ P^{(1)}_{0}(y) = P^{(0)}_{M -1} \circ \cdots \circ P^{(0)}_{0}(y)$ ;

2. (2) $P^{(1)}_{M -1} \circ \cdots \circ P^{(1)}_{0}(z)> P^{(0)}_{M -1} \circ \cdots \circ P^{(0)}_{0}(z) + \delta _{\epsilon , M}(\sigma )$ for every $z \notin y + (- \sigma , \sigma ) + {\mathbb Z}$ and for every $\sigma> 0$ .

Proof. This lemma is obvious if $({\mathcal {H}}, d_{\mathcal {H}}, \iota _{\mathcal {H}})$ is in Example 1, as we can use the projective action given by the parabolic elements in $SL(2, {\mathbb R})$ to make perturbations.

Now we assume that $({\mathcal {H}}, d_{\mathcal {H}}, \iota _{\mathcal {H}})$ is in Example 3.

Fix an arbitrary $x \in X$ . We define a real analytic function $c_x : {\mathbb T} \times {\mathbb R}^2 \to {\mathbb R}$ by

$$ \begin{align*} c_x(y\,\mod \!1, s, t) = F_{g^2(x)} \circ(F_{s+t})_{g(x)} \circ (F_t)_x(y) - F_{g^2(x)} \circ F_{g(x)} \circ F_x(y). \end{align*} $$

By straightforward computation, we see that

(7.3) $$ \begin{align} (f_{- c_x(w, s, t)})_{g^2(x)} \circ (f_{s + t})_{g(x)} \circ (f_t)_x(w) = f_{g^2(x)} \circ f_{g(x)} \circ f_x(w). \end{align} $$

By continuity, we have

(7.4) $$ \begin{align} \lim_{s \to 0} \sup_{x \in X} \sup_{w \in {\mathbb T}} |c_x(w, s, 0)| = 0. \end{align} $$

Moreover, given any $w_0 \in {\mathbb R}$ , we have

$$ \begin{align*} & \partial_t \{ (f_{- c_x(w_0, s, t)})_{g^2(x)} \circ (f_{s + t})_{g(x)} \circ (f_t)_x(w) \}|_{t = 0} \\ &\quad= - \partial_t c_x(w_0, s, t)|_{t = 0} + \partial_t \{ f_{g^2(x)} \circ (f_{s + t})_{g(x)} \circ (f_t)_x(w) \}|_{t = 0} \\ &\quad= - \partial_t c_x(w_0, s, t)|_{t = 0} + \partial_t \{ c_x(w, s, t) \}|_{t = 0}. \end{align*} $$

Fix some $s \in (0, \epsilon / 2)$ sufficiently close to $0$ such that $\sup _{x \in X} \sup _{w \in {\mathbb T}} |c_x(w, s, 0)| < \epsilon / 2$ , and the function $ \partial _t \{ c_x(w, s, t) \}|_{t = 0}$ , as a non-constant real analytic function of w, reaches its minimum on a finite set $C_x \subset {\mathbb T}$ . Then

$$ \begin{align*} \partial_t \{ (f_{- c_x(w, s, t)})_{g^2(x)} \circ (f_{s + t})_{g(x)} \circ (f_t)_x(w) \}|_{t = 0} \geq 0, \end{align*} $$

and the equality holds if and only if $w \in C_x$ . By compactness, there exists an integer $L> 0$ such that $|C_x| \leq L$ for every $x \in X$ .

Define $M {\kern-1pt}={\kern-1pt} 5L$ . We will inductively construct $p^{(j)}_i$ for $j {\kern-1pt}\in{\kern-1pt} \{0,{\kern-1pt}1 \}$ and $i {\kern-1pt}\in{\kern-1pt} \{ 0, \ldots , M{\kern-1pt}-{\kern-1pt}1 \}$ so that the conclusion of the lemma is satisfied.

Denote $C_x = \{ w_0, \ldots , w_{\ell - 1} \}$ , where $\ell \leq L$ . We set $w_{0, i} = w_i$ for $0 \leq i \leq \ell -1$ .

Given an integer $0 \leq m \leq \ell - 1$ , assume that we have already constructed $p_i$ for $i \in \{ 0, \ldots , 5m - 1 \}$ . We define

(7.5) $$ \begin{align} & (p_{5m}, p_{5m + 1}, p_{5m + 2}) \nonumber\\&\quad = ( H( g^{5m}(x)), H( g^{5m + 1}(x) ), H( g^{5m+2}(x) ) ) + (0, s, -c_{g^{5m}(x)}( (f^{5m})_x (w_0), s, 0)). \nonumber\\ \end{align} $$

By our choice of s, we have $(p_{5m}, p_{5m + 1}, p_{5m + 2}) \in \mathcal B_{\mathcal {H}}( H(g^{5m}(x)), \epsilon ) \times \mathcal B_{\mathcal {H}}( H(g^{5m + 1}(x)), \epsilon ) \times \mathcal B_{\mathcal {H}}( H(g^{5m + 2}(x)), \epsilon )$ . We define

$$ \begin{align*} z_{m, i} = \iota_{\mathcal{H}}( ( p_{5m + k} )_{k = 0}^{2} )(w_{m, i})\quad \text{for all } 0 \leq i \leq \ell-1. \end{align*} $$

By Lemma 4.4, there exists $(p_{5m + 3},{\kern-1pt} p_{5m + 4}) {\kern-1pt}\in{\kern-1pt} \mathcal B_{\mathcal {H}}( H(g^{5m + 3}(x)),{\kern-1pt} \epsilon )\! \times \! \mathcal B_{\mathcal {H}}( H(g^{5m + 4}(x)),{\kern-1pt} \epsilon )$ such that

(7.6) $$ \begin{align} \iota_{\mathcal{H}}((p_{5m + 3}, p_{5m + 4}))(z_{m, 0}) &= \iota_{\mathcal{H}}( (H(g^{5m + 3}(x)), H(g^{5m + 4}(x)) ) )(z_{m, 0}), \end{align} $$

(7.7) $$ \begin{align} \iota_{\mathcal{H}}((p_{5m + 3}, p_{5m + 4}))(z_{m, m + 1}) &\not\in C_{g^{5m + 5}(x)} \quad \mbox{if}\ m < \ell - 1. \end{align} $$

We define

$$ \begin{align*} w_{m+1, i} = \iota_{\mathcal{H}}( (p_{5m + 3}, p_{5 m + 4}) )(z_{m, i}) \quad \text{for all } 0 \leq i \leq \ell - 1. \end{align*} $$

We set $p^{(0)}_{k} = p_{k}$ for every $0 \leq k \leq 5\ell -1$ . Let $t> 0$ be a small constant to be determined. For each $0 \leq m \leq \ell -1$ , we define

$$ \begin{align*} (p^{(1)}_{5m}, p^{(1)}_{5m + 1}, p^{(1)}_{5m + 2}) &= ( H( g^{5m}(x)), H( g^{5m + 1}(x) ), H( g^{5m+2}(x) ) ) \\&\quad + (t, s + t, -c_{g^{5m}(x)}( (f^{5m})_x (w_0), s, t)), (p^{(1)}_{5m + 3}, p^{(1)}_{5m + 4} )\\& = (p_{5m + 3}, p_{5m + 4}). \end{align*} $$

We set $p^{(0)}_{k} = p^{(1)}_{k} = H(g^{k}(x))$ for every $5 \ell \leq k \leq M - 1$ . By letting t be sufficiently close to $0$ , we have $d_{\mathcal {H}}(p^{(j)}_k, H(g^{k}(x))) < \epsilon $ for $j \in \{0,1\}$ and $0 \leq k \leq M - 1$ .

Take an arbitrary $y \in {\mathbb R}$ such that $y\,\mod \!1 = w_0$ . It is then straightforward to verify item (1) by equations (7.5) and (7.3). To verify item (2), we take an arbitrary $u \in {\mathbb T}$ and denote $u_k = \iota _{\mathcal {H}}( ( p_i )_{i = 0}^{k - 1} )(u)$ for each $0 \leq k \leq M-1$ . Now we view $p^{(1)}_k$ for each $0 \leq k \leq M-1$ as a function of t. Then we have

$$ \begin{align*} & \partial_t \{ \iota_{\mathcal{H}}( ( p^{(1)}_k )_{k = 0}^{M - 1} )(u) \}|_{t = 0} \\ &\quad = \sum_{ m = 0 }^{ \ell - 1} D\iota_{\mathcal{H}}( ( p_k )_{k = 5m + 3 }^{M-1} )( u_{5m + 3} ) \\ &\qquad \cdot \partial_t \{ (f_{- c_{ g^{5m}(x) }( (f^{5m})_x (w_0) , s, t)})_{g^{5m + 2}(x)} \circ (f_{s + t})_{g^{5m + 1}(x)} \circ (f_t)_{ g^{5m}(x) }( u_{5m} ) \}|_{t = 0}. \end{align*} $$

By construction, we see that for any $u \neq w_0$ , there exists some $0 \leq m \leq \ell - 1$ such that $u_{5m} \notin C_{g^{5m}(x)}$ . Consequently, we have

$$ \begin{align*} \partial_t \{ \iota_{\mathcal{H}}( ( p^{(1)}_k )_{k = 0}^{M - 1} )(u) \}|_{t = 0} \geq 0 \end{align*} $$

with equality if and only if $u = w_0$ . Then it is straightforward to deduce item (2) by compactness.

Now we state the main observation for the proof of Lemma 4.8.

Lemma 7.4. For any $\epsilon> 0$ , there exists a constant $N_2 = N_2(H,\epsilon )> 0$ such that the following is true. For any $(x, y) \in X \times \mathbb {R}$ , there exist integers $M_-, M_+$ satisfying $-N_2 \leq M_- \leq 0\leq M_+ \leq N_2$ such that for any $z_+,z_- \in \mathbb {R}$ with $|z_{+}- (F^{M_+})_x(y)|, |z_{-} - (F^{M_{-}})_x(y)|<2$ , there exist $(p_{M_{-}}, \ldots , p_{M_+-1} ) \in {\mathcal {H}}^{M_+-M_-}$ and $y'\in (y,y+1)$ such that:

1. (1) $d_{\mathcal {H}}(p_i,H(g^i(x)))<\epsilon $ for any $M_- \leq i\leq M_{+}-1$ ;

2. (2) denote by $P_i$ the unique lift of $\iota _{\mathcal {H}}(p_i)$ close to $F_{g^{i}(x)}$ . Then either we have

   $$ \begin{align*} \begin{array}{ccc} & \kern-34pt P_{0} \circ \cdots \circ P_{M_+ - 1}[y,y') \subset (z_+ -\epsilon, z_+ +\epsilon)\\\mbox{ and } & (P_{-1} \circ \cdots \circ P_{M_-} )^{-1}[y',y+1) \subset (z_- -\epsilon,z_- +\epsilon), \end{array} \end{align*} $$

or we have

$$ \begin{align*} \begin{array}{ccc} &\kern-28pt P_{0} \circ \cdots \circ P_{M_+ - 1}[y',y+1) \subset (z_+ -\epsilon, z_+ +\epsilon)\\ \mbox{ and } & (P_{-1} \circ \cdots \circ P_{M_-} )^{-1}[y,y') \subset (z_- -\epsilon,z_- +\epsilon). \end{array} \end{align*} $$

Proof. Without loss of generality, we assume that $\epsilon \in (0, \min (\kappa (H), 1)/2)$ , where $\kappa (H)$ is given by Lemma 7.1.

We let $\epsilon _0 = \epsilon _0(H, \epsilon /2)$ be given by Lemma 2.5. Let

(7.8) $$ \begin{align} m_0 &= \lceil 3 \kappa_1(f, \epsilon_0)^{-1}N_1(f, \epsilon_0) \rceil +1, \end{align} $$

(7.9) $$ \begin{align} \epsilon_2 &= (\Vert f \Vert_{C^{0,1}} + 1)^{-m_0}\epsilon, \end{align} $$

where $\kappa _1$ and $N_1$ are given by Corollary 2.4.

Let $M = M(H, \epsilon )$ be given by Lemma 7.3. Given $x \in X$ and $y \in {\mathbb R}$ , we apply Lemma 7.3 to obtain $(p^{(j)}_i)_{i=0}^{M-1} \in {{\mathcal {H}}}^{M}$ for $j \in \{ 0,1 \}$ and $0 \leq i \leq M-1$ . We denote $(p^{(j)}_i)_{i=0}^{M-1}$ as $(p^{(j)}_{x, y, i})_{i=0}^{M-1}$ to indicate the dependence on x and y.

By Lemma 7.3, we define

(7.10) $$ \begin{align} \ \,\epsilon_1 &= \delta_{\epsilon, M}( \epsilon_2)> 0,\quad\qquad\qquad \end{align} $$

(7.11) $$ \begin{align} \epsilon^{\prime}_1 &= M^{-1}( \Vert f\Vert_{C^{0,1}} + 1)^{-M} \epsilon_1. \end{align} $$

We have for every $x \in X$ , $y \in {\mathbb R}$ , and $y' \not \in \mathbb {Z} + y + (-\epsilon _2,\epsilon _2)$ that

(7.12) $$ \begin{align} P^{(1)}_{x, y, M - 1} \circ \cdots \circ P^{(1)}_{x, y, 0}(y') - P^{(0)}_{x, y, M - 1} \circ \cdots \circ P^{(0)}_{x, y, 0}(y')> \epsilon_1. \end{align} $$

We let

(7.13) $$ \begin{align} m_1 = 3 \lceil \Delta(\epsilon^{\prime}_1)^{-1} \rceil K(\epsilon^{\prime}_1), \end{align} $$

where functions $\Delta , K$ are given by Lemma 7.1.

We fix some $x \in X$ and $y \in {\mathbb R}$ from now on. We define

(7.14) $$ \begin{align} \hat{p}_{kM + i} &= p^{(1)}_{g^{kM}(x), (F^{kM})_x(y), i}, \notag\\\check{p}_{kM + i} &= p^{(0)}_{g^{kM}(x), (F^{kM})_x(y), i}\quad \text{for all } k \in {\mathbb Z},\ 0 \leq i \leq M-1. \end{align} $$

By Lemma 7.3, we have $d_{\mathcal {H}}( \hat {p}_i, H(g^i(x)) ), d_{\mathcal {H}}( \check {p}_i, H(g^i(x)) ) <\epsilon $ for all $i\in \mathbb {Z}$ . We denote by $\hat {P}_i$ , respectively $\check {P}_i$ , the unique lift of $\hat {p}_i$ , respectively $\check {p}_i$ , close to $F_{g^{i}(x)}$ . By equation (7.14) and Lemma 7.3(1), it is direct to verify that for any $i \geq 0, \hat {P}_{i M -1} \cdots \hat {P}_0(y) = \check {P}_{i M -1} \cdots \check {P}_0(y) = (F^{i M})_{x}(y)$ ; and for any $i < 0, \hat {P}^{-1}_{i M} \cdots \hat {P}^{-1}_{-1}(y) = \check {P}^{-1}_{i M}, \ldots \check {P}^{-1}_{-1}(y) = (F^{i M})_x(y)$ .

Define

$$ \begin{align*}N_2 = m_1 M + m_0.\end{align*} $$

We have the following claim.

Claim 7.5. For any $z\in (y,y+1)$ , there exists $0\leq i\leq m_1$ such that

$$ \begin{align*} \hat{P}_{iM-1}\cdots \hat{P}_0(z)\in (F^{iM})_x(y)+(0,\epsilon_2) \cup (1-\epsilon_2,1). \end{align*} $$

Similarly, for any $z\in (y,y+1)$ , there exists $0\leq i\leq m_1$ such that

$$ \begin{align*}\hat{P}^{-1}_{-iM}\cdots \hat{P}^{-1}_{-1}(z) \in (F^{-iM})_x(y)+ (0,\epsilon_2)\cup (1-\epsilon_2,1). \end{align*} $$

Proof. We will only detail the first statement, since the second one follows from a similar argument. If the first statement is false, let $z_i = \hat {P}_{iM -1}\cdots \hat {P}_0(z)$ for all $0 \leq i \leq m_1$ , then we would have

$$ \begin{align*} z_i \not\in\mathbb{Z}+ (F^{i M})_x(y)+ (-\epsilon_2,\epsilon_2)\quad \text{for all } 0\leq i\leq m_1. \end{align*} $$

Then by equation (7.12), we have

(7.15) $$ \begin{align} \hat{P}_{(i+1)M - 1} \circ \cdots \circ \hat{P}_{iM}(z_i)& > \check{P}_{(i+1)M - 1} \circ \cdots \circ \check{P}_{iM}(z_i) + \epsilon_1 \nonumber \\ & \geq (\check{P}_{(i+1)M - 1})_{\epsilon^{\prime}_1} \circ \cdots \circ (\check{P}_{iM})_{\epsilon^{\prime}_1}(z_i). \end{align} $$

By Corollary 7.2, and equations (7.13) and (7.15), we would have

$$ \begin{align*} & \hat{P}_{m_1 M -1}\cdots \hat{P}_0(y+1)\\ &\quad \geq \hat{P}_{m_1 M -1} \cdots \hat{P}_0(z) \geq (\check{P}_{m_1M - 1})_{\epsilon^{\prime}_1} \circ \cdots \circ (\check{P}_{0})_{\epsilon^{\prime}_1}(y)> (F^{m_1 M})_x(y)+2. \end{align*} $$

This is a contradiction.

Let

$$ \begin{align*} U_- &=\{z\in (y,y+1)\mid \mbox{there exists } 0\leq i\leq m_1\ \mbox{such that}\\&\quad\ \ \hat{P}_{iM-1}\cdots \hat{P}_0(z)\in (F^{iM})_x(y)+(0,\epsilon_2)\}, \\U_+ &=\{z\in (y,y+1)\mid \mbox{there exists } 0\leq i\leq m_1\ \mbox{such that}\\&\quad\ \ \hat{P}_{iM-1}\cdots \hat{P}_0(z)\in (F^{iM})_x(y)+(1-\epsilon_2,1)\}. \end{align*} $$

Then by our claim, we have

$$ \begin{align*}U_- \cup U_+ = (y,y+1).\end{align*} $$

It is direct to see that $U_-, U_+$ are both non-empty connected open sets. Since $(y, y + 1)$ is connected, we conclude that $U_- \cap U_+\neq \emptyset $ . We take $y'$ to be an arbitrary element in $U_- \cap U_+$ .

Again by Claim 7.5, there exists $0 \leq n^{\prime }_- \leq m_1$ such that for $N^{\prime }_- = M n^{\prime }_-$ , we have

$$ \begin{align*}\hat{P}^{-1}_{-N^{\prime}_{-}} \cdots \hat{P}^{-1}_{-1}(y')\in (F^{-N^{\prime}_{-}})_x(y)+(0,\epsilon_2)\cup(1-\epsilon_2,1).\end{align*} $$

Without loss of generality, we may assume that

$$ \begin{align*}\hat{P}^{-1}_{-N^{\prime}_{-}} \cdots \hat{P}^{-1}_{-1}(y')\in (F^{-N^{\prime}_{-}})_x(y)+(0,\epsilon_2),\end{align*} $$

as the other case can be dealt with by a similar argument. Then we have

$$ \begin{align*}\hat{P}^{-1}_{-N^{\prime}_{-}} \cdots \hat{P}^{-1}_{-1}[y,y')\subset (F^{-N^{\prime}_{-}})_x(y)+[0,\epsilon_2).\end{align*} $$

By $y' \in U_+$ , we see that there exists $n^{\prime }_+ \in \{0, \ldots , m_1 \}$ such that for $N^{\prime }_+ = M n^{\prime }_+$ , we have

$$ \begin{align*} \hat{P}_{N^{\prime}_{+}-1} \cdots \hat{P}_0(y') \in (F^{N^{\prime}_+})_x(y)+(1-\epsilon_2,1). \end{align*} $$

Hence,

(7.16) $$ \begin{align} \hat{P}_{N^{\prime}_{+}-1} \cdots \hat{P}_0[y',y+1)\subset (F^{N^{\prime}_+})_x(y)+(1-\epsilon_2,1). \end{align} $$

We set

$$ \begin{align*} M_+=N^{\prime}_+ +m_0\quad\mbox{and}\quad p_i = \hat{p}_i,\quad P_i=\hat{P}_i\quad \text{for all } 0 \leq i \leq N^{\prime}_+ -1. \end{align*} $$

By Lemma 2.5, equation (7.8), and the fact that

$$ \begin{align*} (F^{m_0})_{g^{N^{\prime}_+}(x)}\hat{P}_{N^{\prime}_{+}-1} \cdots \hat{P}_0(y+1) = (F^{M_+})_x(y+1)\in z_+ +(-3,3), \end{align*} $$

there exists $(p_{N^{\prime }_+}, \ldots , p_{M_+ -1} )\in {\mathcal {H}}^{m_0}$ such that:

1. (1) $d_{\mathcal {H}}(p_{N^{\prime }_+ +i}, H(g^{N^{\prime }_+ +i}(x)) )<\epsilon $ for any $0\leq i\leq m_0-1$ ;

2. (2) $P_{M_+ -1}\cdots P_{N^{\prime }_+} ( (F^{N^{\prime }_+})_x (y)+1)=z_+$ ,

where $P_i$ is a lift of $\iota _{\mathcal {H}}(p_i)$ close to $F_{g^{i}(x)}$ for each $N^{\prime }_+ \leq i \leq M_+ - 1$ . Then by equations (7.16) and (7.9), we have

$$ \begin{align*} P_{M_+-1}\cdots P_0[y',y+1) &\subset P_{M_+-1}\cdots P_{N^{\prime}_+}( (F^{N^{\prime}_+})_x(y)+(1-\epsilon_2,1])\\ &\subset (z_+-\epsilon, z_++\epsilon). \end{align*} $$

By a similar method, we may set

$$ \begin{align*} M_- = - N^{\prime}_- - m_0, \end{align*} $$

and define $(p_{M_-}, \ldots, p_{-1})$ and a lift $P_i$ of $\iota _{\mathcal {H}}(p_i)$ for each $M_- \leq i \leq - 1$ . It is then direct to verify items (1) and (2).

We also need the following two lemmata. In the following, we denote by $y_i$ a point in ${\mathbb R}$ , and denote $\bar {y}_i = y_i\,\mod {\mathbb Z} \in {\mathbb T}$ .

Lemma 7.6. For any $\epsilon , \eta> 0$ , there exist $\epsilon _3 = \epsilon _3(H,\epsilon )> 0$ , $r_1 = r_1(H,\epsilon , \eta )> 0$ , $N_3 = N_3(H , \epsilon )> 0$ such that for any integer $N \geq N_3$ , the following is true.

(Forward contraction) For any $x\in X$ , there exist $y_1\in \mathbb {R}$ and $(q_0,\ldots , q_{N-1})\in {\mathcal {H}}^N$ such that:

1. (1) $d_{\mathcal {H}}(q_{i}, H(g^{i}(x)))<\epsilon $ for every $0\leq i\leq N-1$ ;

2. (2) $D(\iota _{\mathcal {H}}((q_j)_{j=0}^{i-1}))(\bar {y}_1)<e^{-2\epsilon _3i}$ for every $N_3 \leq i\leq N$ ;

3. (3) $({D\iota _{\mathcal {H}}((q_j)_{j=0}^{i -1})(\bar {y}') }/{D\iota _{\mathcal {H}}((q_j)_{j=0}^{i -1})(\bar {y}_1) }) \in (e^{- \min (\epsilon _3, \eta ) i}, e^{ \min (\epsilon _3, \eta ) i})$ for every $0 \leq i \leq N$ and every $\bar {y}'\in (\bar {y}_1- r_1, \bar {y}_1 + r_1)$ ;

4. (4) $\iota _{\mathcal {H}}((q_j)_{j=0}^{N -1})(\bar {y}_1)= (f^{N})_x(\bar {y}_1)$ .

(Backward contraction) For any $x \in X$ , there exist $y_2 \in {\mathbb R}$ and $(q_{-N}, \ldots , q_{-1}) \in {\mathcal {H}}^N$ such that:

1. (1′) $d_{\mathcal {H}}(q_{-i}, H(g^{-i}(x)))<\epsilon $ for every $1\leq i\leq N$ ;

2. (2′) $D(\iota _{\mathcal {H}}((q_j)_{j=-i}^{-1})^{-1})(\bar {y}_2) <e^{-2\epsilon _3i}$ for every $N_3 \leq i\leq N$ ;

3. (3′) $({D( \iota _{\mathcal {H}}((q_j)_{j= -i}^{-1})^{-1} )(\bar {y}') }/{D( \iota _{\mathcal {H}}((q_j)_{j= -i}^{-1})^{-1}) (\bar {y}_2) }) \in (e^{-\min (\epsilon _3, \eta ) i}, e^{\min (\epsilon _3, \eta ) i})$ for every $0 \leq i \leq N$ and every $\bar {y}'\in (\bar {y}_2- r_1, \bar {y}_2 + r_1)$ ;

4. (4′) $\iota _{\mathcal {H}}((q_j)_{j=0}^{N -1})(\bar {y}_2)= (f^{N})_x(\bar {y}_2)$ .

Proof. We will detail the proof of the case (Forward contraction). The other case follows from a similar argument.

We fix a small constant $\sigma _0> 0$ such that for every $x \in X$ and $w \in {\mathbb T}$ , we have

$$ \begin{align*} E(\sigma_0, w, x, H) \in \prod_{i=0}^{k-1} \mathcal B_{\mathcal{H}}(H(g^{i}(x)), \epsilon), \end{align*} $$

where the map E is given by Lemma 4.3. We let $r_0, \epsilon _2$ be given by Lemma 4.3(3) for $\sigma _0$ .

Fix an arbitrary $x \in X$ . For any integer $n\geq 1$ , we define

$$ \begin{align*} A_{n,\epsilon_2} = \{ w \in \mathbb{T}\mid D(f^n)_x(w)> 1000 k \epsilon_2^{-1} e^{n\epsilon_2/(100k)}\}.\end{align*} $$

By the identity in equation (2.2) and Markov’s inequality, we have

$$ \begin{align*}\bigg| \bigcup_{n\geq 1}A_{n,\epsilon_2}\bigg| \leq \sum_{n\geq 1} |A_{n,\epsilon_2}|<\sum_{n\geq 1} \frac{\epsilon_2}{1000 k}e^{-n\epsilon_2/(100k)}<1.\end{align*} $$

We fix an arbitrary $\bar {y}_1\in \mathbb {T}\setminus (\bigcup _{n\geq 1} A_{n,\epsilon _2})$ .

We let $N_3> 0$ be a large integer to be determined depending only on H and $\epsilon $ , and let

(7.17) $$ \begin{align} \epsilon_3 = \epsilon_2/(100 k). \end{align} $$

By the choice of $\bar {y}_1$ and by letting $N_3$ be sufficiently large, we have

(7.18) $$ \begin{align} D(f^n)_x(\bar{y}_1)\leq 1000 k \epsilon_2^{-1}e^{n\epsilon_2/(100k)} < e^{n\epsilon_2/(50k)} = e^{2n\epsilon_3}\quad \text{for all } n\geq N_3. \end{align} $$

For any $N\geq N_3$ , we define

(7.19) $$ \begin{align} (q_{ik+j} )_{j=0}^{k-1} = E(\sigma_0, (f^{ik})_x(\bar{y}_1), g^{ik}(x), H)\quad \text{for all } 0 \leq i \leq \lfloor (N - 1)/k \rfloor - 1 \end{align} $$

and define

$$ \begin{align*} q_j = H(g^{j}(x))\quad \text{for all } k \lfloor (N - 1)/k \rfloor \leq j < N. \end{align*} $$

Then item (1) follows from our choice of $\sigma _0$ . It is direct to verify item (4) by Lemma 4.3(2).

We let $r'>0$ be a small constant depending only on $H, {{\mathcal {H}}}, k$ , and $\epsilon $ such that

(7.20) $$ \begin{align} \frac{D(f^{k})_{x'}(\bar y")}{D(f^{k})_{x'}(\bar y')} < e^{\min( \epsilon_3, \eta) / 2}\quad \text{for all } x' \in X, |\bar{y}'- \bar{y}"| < 2r' \end{align} $$

and

(7.21) $$ \begin{align} \frac{DE(\sigma_0, w, x', H)(\bar y")}{DE(\sigma_0, w, x', H)(\bar y')} < e^{\min( \epsilon_3, \eta) / 2}\quad \text{for all } x' \in X, |\bar y'- \bar y"| < 2r'. \end{align} $$

By equations (7.17), (7.18), (7.19), and Lemma 4.3(3), we have

(7.22) $$ \begin{align} D(\iota_{\mathcal{H}}((q_i)_{i=0}^{n-1}))(\bar{y}_1)< e^{- n\epsilon_2/2k} = e^{ - 50 n \epsilon_3}\quad \text{for all } N_3 \leq n \leq N. \end{align} $$

This proves item (2). We choose $r_1 = r_1(H, \epsilon , \eta ) \in ( 0, r')$ to be sufficiently small, so that we have

$$ \begin{align*} \iota_{\mathcal{H}}((q_i)_{i=0}^{n-1})(\bar{y}_1-r_1, \bar{y}_1 +r_1)\subset (f^n)_x(\bar{y}_1) + (-r',r')\quad \text{for all } 0\leq n\leq N_3. \end{align*} $$

By equations (7.21), (7.22) and a simple induction, we obtain item (3).

Lemma 7.7. For any $\eta>0$ , there exists $r_2 =r_2(H,\eta )>0$ such that for any integer ${N\geq 1}$ , the following is true.

(Forward expansion) For any $x\in X$ , there exists $\bar {y}_3 \in \mathbb {T}$ such that $D(f^N)_x(\bar {y}')> e^{-\eta N}$ for any $\bar {y}' \in (\bar {y}_3 - r_2\Vert f\Vert ^{-N}_{C^{0,1}}, \bar {y}_3+r_2\Vert f\Vert ^{-N}_{C^{0,1}})$ .

(Backward expansion) For any $x\in X$ , there exists $\bar {y}_4 \in \mathbb {T}$ such that $D(f^{-N})_x(\bar {y}')> e^{-\eta N}$ for any $\bar {y}'\in (\bar {y}_4 - r_2\Vert f\Vert ^{-N}_{C^{0,1}}, \bar {y}_4+r_2\Vert f\Vert ^{-N}_{C^{0,1}}).$

Proof. By equation (2.2), we can choose $\bar {y}_3 \in \mathbb {R}$ so that $D(f^N)_x(\bar {y}_3) = 1$ . Then by letting $r_2$ be sufficiently small, and by continuity, we can verify (Forward expansion). The proof of (Backward expansion) is similar.

Proof of Lemma 4.8

As before, we denote $f = \Phi (H)$ . We set

$$ \begin{align*} D= \Vert f\Vert_{C^{0,1}} + 3 \ (\mbox{so that}\ \log D \geq 1), \quad \eta = \bigg(\frac{L_+(f)-L_-(f)}{100 \log D }\bigg)^2> 0. \end{align*} $$

We denote $n_1 = N^{\prime }_0(H, \eta )> 0$ , where $N^{\prime }_0$ is given by Lemma 2.8. Then for any $n\geq n_1$ , we have

(7.23) $$ \begin{align} e^{(L_-(f)-\eta)n} < D(f^n)_x( w ) < e^{(L_+(f)+\eta)n}\quad \text{for all } (x, w)\in X\times\mathbb{T}. \end{align} $$

By continuity and subadditivity, it is direct to see that there exists $\epsilon '=\epsilon '(H, \eta )>0$ such that for any $n\geq n_1$ , for any $(h_0,\ldots , h_{n-1})\in {\mathcal {H}}^n$ satisfying $d_{\mathcal {H}}(h_i,H(g^i(x)))<\epsilon '$ for all $0\leq i\leq n-1$ , we have

$$ \begin{align*} e^{(L_-(f)-2\eta)n} < D(\iota_{\mathcal{H}}((h_i)_{i=0}^{n-1}))(w) < e^{(L_+(f)+2\eta)n}\quad \text{for all } (x, w) \in X \times \mathbb{T}. \end{align*} $$

Without loss of generality, we can assume that $\epsilon \in (0, \epsilon ')$ . We let $\epsilon _3 =\epsilon _3(H,\epsilon ), r_1 =r_1(H,\epsilon , \eta ), N_3 =N_3(H,\epsilon )$ be given by Lemma 7.6. We let $r_2 = r_2(H, \eta )> 0$ be given by Lemma 7.7. Denote

$$ \begin{align*} r_0 = r_0(H, \epsilon) = \min( r_1, r_2,\epsilon)/2. \end{align*} $$

Let $N_2 = N_2(H, r_0)$ be given by Lemma 7.4. It is clear that, ultimately, $N_2$ depends only on H and $\epsilon $ .

We let $\epsilon _0 = \epsilon _0(H, \epsilon /2)$ be given by Lemma 2.5. Define

(7.24) $$ \begin{align} m_2 = \lceil 2\kappa_1(\Phi(H), \epsilon_0)^{-1}N_1(\Phi(H), \epsilon_0)\rceil+1, \end{align} $$

where $\kappa _1, N_1$ are given Lemma 2.5.

We let $N_4> 0$ be a large integer to be determined depending only on H and $\epsilon $ . Taking an arbitrary integer $N>N_4$ , we set

$$ \begin{align*}x_0=g^{\lceil {N}/{2}\rceil}(x).\end{align*} $$

We apply Lemma 7.4 for $(r_0, x_0, 0)$ in place of $(\epsilon , x, y)$ to obtain $(M_1, M_2)$ in place of $(M_+,M_-)$ . We have $-N_2 \leq M_2 \leq 0\leq M_1 \leq N_2$ .

By letting $N_4$ be sufficiently large, we have $N -\lceil {N}/{2}\rceil - M_1>N_3$ . Then by Lemma 7.6 (Forward contraction) for $(g^{M_1}(x_0),N-\lceil {N}/{2} \rceil -M_1)$ in place of $(x,N)$ , we obtain $\bar {y}_1\in {\mathbb T}$ and $\tilde {p}_0,\ldots ,\tilde {p}_{N-\lceil {N}/{2} \rceil -M_1-1} \in {\mathcal {H}}$ , such that:

1. (g1) $d_{\mathcal {H}}(\tilde {p}_i,H(g^{M_1+i}(x_0)) ) <\epsilon $ for all $0\leq i\leq N-\lceil {N}/{2}\rceil -M_1-1$ ;

2. (g2) $D\iota _{\mathcal {H}}((\tilde {p}_{j})_{j = 0}^{i-1})(\bar {y}_1) < e^{-2\epsilon _3 i}$ for all $N_3\leq i\leq N-\lceil {N}/{2}\rceil -M_1-1$ ;

3. (g3) $({D \iota _{\mathcal {H}}((\tilde {p}_j)_{j=0}^{i-1})(\bar {y}') }/{D \iota _{\mathcal {H}}((\tilde {p}_j)_{j=0}^{i-1})(\bar {y}_1) }) \in (e^{-\min (\eta ,\epsilon _3) i}, e^{\min (\eta ,\epsilon _3) i})$ for any $0 \leq i\leq N-\lceil {N}/{2}\rceil -M_1-1$ and any $\bar {y}'\in (\bar {y}_1-r_1, \bar {y} + r_1)$ ;

4. (g4) $\iota _{\mathcal {H}}((\tilde {p}_j)_{j=0}^{N-\lceil {N}/{2}\rceil -M_1-1})(\bar {y}_1) = ( f^{N-\lceil {N}/{2}\rceil -M_1})_{g^{M_1}(x_0)}(\bar {y}_1)$ .

Without loss of generality, we may assume that the lifts of $\bar {y}_1$ and $\bar {y}^{\prime }_1$ , denoted by ${y_1, y^{\prime }_1 \in {\mathbb R}}$ , respectively, satisfy that

$$ \begin{align*} \vert (F^{M_1})_{x_0}(0)-y_1\vert, \vert (F^{M_2})_{x_0}(0)-y^{\prime}_1\vert <2. \end{align*} $$

We denote by $\tilde {P}_i$ the unique lift of $\iota _{\mathcal {H}}(\tilde {p}_i)$ close to $F_{g^{M_1 + i}(x_0)}$ for every $0 \leq i \leq N -\lceil {N}/{2}\rceil - M_1- 1$ . Then by $r_0 < r_1$ and item (g3), for any $1\leq i\leq N -\lceil {N}/{2}\rceil - M_1$ , we have

(7.25) $$ \begin{align} \frac{D(\tilde{P}_{i-1}\cdots\tilde{P}_0)(y')}{D(\tilde{P}_{i-1}\cdots\tilde{P}_0)(y_1)} \in (e^{-i\min(\eta,\epsilon_3)},e^{i\min(\eta,\epsilon_3)})\quad \text{for all } y'\in(y_1-r_0,y_1+r_0). \end{align} $$

By Lemma 7.4 for $(r_0, y_1, y^{\prime }_1)$ in place of $(\epsilon , z_+, z_-)$ , we obtain $y^{\prime }_0\in (0,1)$ and $(\hat {p}_{M_2},\ldots , \hat {p}_{M_1-1})\in {{\mathcal {H}}}^{M_1-M_2}$ such that $d_{\mathcal {H}}(\hat {p}_i,H( g^i(x_0)) )<r_0\leq \epsilon $ for all $M_2\leq i\leq M_1-1$ , and, denote by $\hat {P}_i$ the lift of $\iota _{\mathcal {H}}(\hat {p}_i)$ close to $F_{g^{i}(x_0)}$ , we have:

1. Case I. Either

   (7.26) $$ \begin{align} \hat{p}_{M_1-1}\cdots \hat{p}_0[0,y^{\prime}_0) &\subset (y_1-r_0,y_1 + r_0), \end{align} $$
   (7.27) $$ \begin{align} \hat{p}^{-1}_{M_2}\cdots \hat{p}_{-1}^{-1}[y^{\prime}_0,1) &\subset (y^{\prime}_1-r_0, y^{\prime}_1+ r_0); \end{align} $$

2. Case II. Or

   (7.28) $$ \begin{align} \hat{p}_{M_1-1}\cdots \hat{p}_0[y^{\prime}_0,1) &\subset (y_1-r_0, y_1+r_0), \end{align} $$
   (7.29) $$ \begin{align} \hat{p}^{-1}_{M_2}\cdots \hat{p}_{-1}^{-1}[0,y^{\prime}_0) &\subset (y^{\prime}_1-r_0, y^{\prime}_1 +r_0). \end{align} $$

We will only detail the proof for Case I, as the other case follows from a similar argument.

We now define $p_{\lceil {N}/{2}\rceil }, \ldots ,p_{N-1}$ . Take an arbitrary integer

(7.30) $$ \begin{align} m_1\in \bigg(\frac{9\log D (N - \lceil N/2 \rceil)}{9\log D+L_+(f)-L_-(f)}, \frac{(9\log D+\eta) (N - \lceil N/2 \rceil)}{9\log D+L_+(f)-L_-(f)}\bigg). \end{align} $$

Define

$$ \begin{align*} &x_1 = g^{M_1}(x_0), \quad x_2=g^{m_1}(x_1),\\ &x_3 =g^{m_2}(x_2), \quad m_3=N-\bigg\lceil \frac{N}{2}\bigg\rceil -M_1-m_1-m_2. \end{align*} $$

By direct computations and by letting $N_4$ be sufficiently large, we see that

(7.31) $$ \begin{align} m_3 \in \bigg( \frac{ (L_+(f)-L_-(f)-2\eta) (N - \lceil N/2 \rceil) }{9\log D+L_+(f)-L_-(f)}, \frac{(L_+(f)-L_-(f) - \eta) (N - \lceil N/2 \rceil)}{9\log D+L_+(f)-L_-(f)}\bigg). \end{align} $$

Then we have

(7.32) $$ \begin{align} N_2 + m_2 = N - \lceil N/2 \rceil - m_1 - m_3 \in \bigg( 0, \frac{ 2\eta(N - \lceil N/2 \rceil) }{9\log D+L_+(f)-L_-(f)}\bigg). \end{align} $$

We define

(7.33) $$ \begin{align} \!\!\qquad p_{\lceil{N}/{2}\rceil +i} &= \hat{p}_i\quad \text{for all } 0\leq i\leq M_1-1, \end{align} $$

(7.34) $$ \begin{align} \!p_{\lceil{N}/{2}\rceil+M_1+i} &= \tilde{p}_i\quad \text{for all } 0\leq i\leq m_1-1, \end{align} $$

(7.35) $$ \begin{align} p_{\lceil{N}/{2}\rceil +M_1+m_1+m_2+i} &= H( g^i(x_3) )\quad \text{for all } 0\leq i\leq m_3-1. \end{align} $$

By equation (7.30) and by letting $N_4$ be sufficiently large, we have $m_1> N_3$ . Then by item (g2) and equation (7.25), we have

(7.36) $$ \begin{align} \tilde{P}_{m_1-1}\cdots\tilde{P}_0(y_1-r_0,y_1+r_0) & \subset\! (F^{m_1})_{x_1}(y_1) + e^{\min(\eta,\epsilon_3)m_1}D(\tilde{P}_{m_1-1}\!\cdots\!\tilde{P}_0)(y_1)(-r_0,r_0) \nonumber \\ & \subset\! (F^{m_1})_{x_1}(y_1) + e^{-\epsilon_3 m_1}(-r_0,r_0). \end{align} $$

By $r_0 \leq r_2$ and Lemma 7.7(Forward expansion) for $(x_3, m_3)$ in place of $(x, N)$ , there exists $y_3\in \mathbb {R}$ , such that

(7.37) $$ \begin{align} D(F^{m_3})_{x_3}(y')> e^{-\eta m_3}\quad \text{for all } y'\in (y_3 -D^{-m_3}r_0, y_3+ D^{-m_3}r_0).\end{align} $$

Without loss of generality, we can choose $y_3$ so that $\vert (F^{m_1+m_2})_{x_1} (y_1) - y_3\vert < 2$ . By equation (7.24), we have $(x_2, (F^{m_1})_{x_1}(y_1) , y_3) \in \Omega _{m_2}(F, \kappa _1(\Phi (H), \epsilon _0) )$ . Then by Lemma 2.5 and $m_2> N_1(\Phi (H), \epsilon _0)$ , we can define $(p_{\lceil {N}/{2}\rceil +M_1+m_1},\ldots , p_{\lceil {N}/{2}\rceil +M_1+m_1+m_2-1})$ so that:

1. (1) $d_{{{\mathcal {H}}}}(p_{\lceil {N}/{2}\rceil +M_1+m_1+i}, H(g^i(x_2)))<\epsilon $ for all $0\leq i\leq m_2-1$ ;

2. (2) we have

   (7.38) $$ \begin{align} P_{\lceil{N}/{2}\rceil+M_1+m_1+m_2-1} \cdots P_{\lceil{N}/{2}\rceil+M_1}(y_1) = y_3. \end{align} $$

Here we denote by $P_{i}$ the unique lift of $\iota _{\mathcal {H}}(p_i)$ close to $F_{g^{i}(x)}$ for every $\lceil {N}/{2}\rceil \leq i \leq N -1$ . Notice that by item (1) above, we have

(7.39) $$ \begin{align} D^{-m_2} < \|D \iota_{\mathcal{H}}((p_{\lceil{N}/{2}\rceil+M_1+m_1+i})_{i=0}^{m_2-1})\| <D^{m_2}. \end{align} $$

We now estimate $D(P_{N-1}\cdots P_{\lceil {N}/{2}\rceil })$ over the interval $[0,y^{\prime }_0)$ . Fix an arbitrary $y'\in [0,y^{\prime }_0)$ . By equations (7.26) and (7.33), we have

(7.40) $$ \begin{align} P_{\lceil{N}/{2} \rceil +M_1-1}\cdots P_{\lceil {N}/{2}\rceil}(y')\in (y_1-r_0, y_1+r_0). \end{align} $$

Then by equations (7.25), (7.39), and (7.38), we have

(7.41) $$ \begin{align} &P_{\lceil {N}/{2}\rceil+M_1+m_1+m_2-1}\cdots P_{\lceil {N}/{2}\rceil}(y') \nonumber\\ &\in y_3 + D ^{m_2} e^{\eta m_1} D(P_{\lceil{{N}/{2}\rceil +M_1+m_1-1}} \cdots P_{\lceil {N}/{2}\rceil+M_1})(y_1) (-r_0, r_0). \end{align} $$

Upper bound. It is direct to see that

(7.42) $$ \begin{align} D(P_{\lceil{N}/{2}\rceil+M_1-1}\cdots P_{\lceil{N}/{2}\rceil})(y') < D^{M_1}. \end{align} $$

By equation (7.40), items (g2), (g3), and equation (7.34), we have

(7.43) $$ \begin{align} &D(P_{\lceil {N}/{2}\rceil+M_1+m_1-1}\cdots P_{\lceil {N}/{2}\rceil+M_1})(P_{\lceil {N}/{2}\rceil+M_1-1}\cdots P_{\lceil {N}/{2}\rceil}(y')) \nonumber \\ &\quad < e^{m_1\epsilon_3} D(P_{\lceil{{N}/{2}}\rceil+M_1+m_1-1}\cdots P_{\lceil{{N_2}/{2}}\rceil+M_1})(y_1)< e^{-m_1\epsilon_3}. \end{align} $$

By equation (7.31) and by letting $N_4$ be sufficiently large, we have $m_3> n_1$ . Then by equations (7.23), (7.42), (7.43), (7.39), (7.30), and (7.31), we have

$$ \begin{align*} D(P_{N-1}\cdots P_{\lceil {N}/{2}\rceil})(y') & < e^{(L_+(f)+\eta)m_3} e^{-m_1\epsilon_3} D^{M_1+m_2},\\ &< e^{({1}/{3})(L_+(f)-L_-(f))(N-\lceil{N}/{2}\rceil)}. \end{align*} $$

Lower bound. We have

(7.44) $$ \begin{align} D(P_{\lceil{N}/{2}\rceil+M_1-1}\cdots P_{\lceil{N}/{2}\rceil})(y')> D^{-M_1}. \end{align} $$

By equation (7.43), it is useful to divide the estimate into the following two cases.

• • If $D(P_{\lceil {{N}/{2}\rceil +M_1+m_1-1}} \cdots P_{\lceil {N}/{2}\rceil +M_1})(y_1)> e^{- ({L_+(f)-L_-(f)}/{4})m_1}$ , then by equations (7.25), (7.40), and (7.34), we have

  $$ \begin{align*} & D(P_{\lceil {N}/{2} \rceil+M_1+m_1-1}\cdots P_{\lceil{N}/{2}\rceil +M_1})(P_{\lceil{N}/{2} \rceil+M_1-1}\cdots P_{\lceil{N}/{2} \rceil}(y') ) \\ &\quad> e^{-m_1\eta}D(P_{\lceil {N}/{2} \rceil+M_1+m_1-1}\cdots P_{\lceil {N}/{2} \rceil+M_1})(y_1)> e^{(- ({L_+(f)-L_(f)}/{4}) -\eta)m_1}. \end{align*} $$
  Then by equation (7.23) and $m_3> n_1$ , we have
  (7.45) $$ \begin{align} D(P_{N_1}\cdots P_{\lceil{N}/{2}}\rceil)(y')> e^{(L_-(f)-\eta)m_3}e^{(-({L_+(f)-L_-(f)}/{4}) - \eta)m_1} D^{-M_1-m_2}. \end{align} $$

• • If $(P_{\lceil {N}/{2} \rceil +M_1+m_1-1}\cdots P_{\lceil {N}/{2}\rceil +M_1})(y_1)\leq e^{-({L_+(f)-L_-(f)}/{4})m_1}$ , then by equations (7.38), (7.30), and (7.31), we have

  $$ \begin{align*} \mbox{right-hand side of equation }({7.41}) \subset y_3+ D^{m_2}e^{(\eta- ({L_+(f)-L_-(f)}/{4}))m_1}(-r_0,r_0) \subset y_3+ D^{-m_3}(-r_0,r_0). \end{align*} $$

The last inclusion follows from equations (7.30) and (7.31). Then by equation (7.37), we have

$$ \begin{align*} D(P_{N-1} \cdots P_{\lceil {N}/{2}\rceil+M_1+m_1+m_2})(P_{\lceil {N}/{2}\rceil+M_1+m_1+m_2-1}\cdots P_{\lceil {N}/{2}\rceil}(y') )> e^{-m_3 \eta}. \end{align*} $$

Moreover, by $ d_{\mathcal {H}}(\tilde {p}_i,H(g^{M_1+i}(x_0)))<\epsilon <\epsilon '$ for all $0\leq i\leq m_1-1$ , by $m_1>n_1$ , and by the choice of $\epsilon '$ , we have

$$ \begin{align*} D(P_{\lceil {N}/{2} \rceil +M_1+m_1-1}\cdots P_{\lceil {N}/{2}\rceil +M_1})(y")> e^{(L_-(f)-2\eta)m_1}\quad \text{for all } y" \in \mathbb{R}. \end{align*} $$

By combining the above inequalities with equations (7.35), (7.39), and (7.44), we obtain

(7.46) $$ \begin{align} D(P_{N-1} \cdots P_{\lceil {N}/{2} \rceil})(y')> e^{ - \eta m_3} e^{(L_-(f) - 2\eta) m_1} D^{- M_1 -m_2}. \end{align} $$

By equations (7.30), (7.31), and (7.32), we can deduce from both equations (7.45) and (7.46) that

$$ \begin{align*} D(P_{N-1}\cdots P_{\lceil {N}/{2}\rceil})(y')> e^{- (1- \eta )\max(L_+(f),-L_-(f))(N-\lceil {N}/{2} \rceil)}. \end{align*} $$

Now, continue to assume that we are under Case I, then we can define $p_0, \ldots , p_{\lceil {N}/{2}\rceil -1}$ in a similar way so that for any $y' \in [y^{\prime }_0, 1)$ , we have

$$ \begin{align*} |\!\log | D(\iota_{\mathcal{H}}((p_i)_{i=0}^{\lceil {N}/{2}\rceil-1} ) )^{-1}(y') | | \leq (1- \eta )\max(L_+(f),-L_-(f)) \bigg\lceil \frac{N}{2} \bigg\rceil. \end{align*} $$

It is then straightforward to verify items (1) and (2) of Lemma 4.8 for Case I. The proof for Case II follows from a similar argument.