Dynamical decompositions of 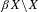$\unicode[STIX]{x1D6FD}X\setminus X$

Abstract

Let 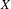$X$ be a locally compact, $\unicode[STIX]{x1D70E}$ -compact, non-compact Hausdorff space and let 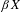$\unicode[STIX]{x1D6FD}X$ be the Stone-Čech compactification of 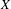$X$ . Let 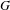$G$ be a countably infinite discrete group continuously acting on 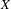$X$ , and suppose that, for every 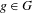$g\in G$ , 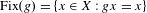$\text{Fix}(g)=\{x\in X:gx=x\}$ is compact. The action of 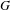$G$ on 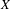$X$ induces the action on 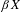$\unicode[STIX]{x1D6FD}X$ , and so on 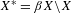$X^{\ast }=\unicode[STIX]{x1D6FD}X\setminus X$ . Let 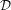${\mathcal{D}}$ denote the finest decomposition of 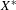$X^{\ast }$ into closed invariant subsets such that the corresponding quotient space of 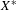$X^{\ast }$ is Hausdorff. Such a decomposition can be defined for any action of 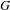$G$ on a compact Hausdorff space. Applying it to every member of 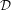${\mathcal{D}}$ gives us a decomposition 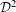${\mathcal{D}}^{2}$ of 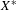$X^{\ast }$ , then 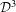${\mathcal{D}}^{3}$ , and so on. We show that (1) 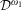${\mathcal{D}}^{\unicode[STIX]{x1D714}_{1}}$ is the coarsest decomposition of 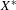$X^{\ast }$ into closed invariant topologically transitive subsets, (2) there is a dense subset of points 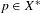$p\in X^{\ast }$ such that 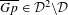$\overline{Gp}\in {\mathcal{D}}^{2}\setminus {\mathcal{D}}$ , in particular, 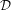${\mathcal{D}}$ is non-trivial and 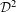${\mathcal{D}}^{2}$ is finer than 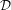${\mathcal{D}}$ , and (3) for every ordinal 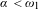$\unicode[STIX]{x1D6FC}<\unicode[STIX]{x1D714}_{1}$ , there is 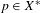$p\in X^{\ast }$ such that 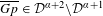$\overline{Gp}\in {\mathcal{D}}^{\unicode[STIX]{x1D6FC}+2}\setminus {\mathcal{D}}^{\unicode[STIX]{x1D6FC}+1}$ , so all the decompositions 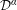${\mathcal{D}}^{\unicode[STIX]{x1D6FC}}$ , 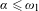$\unicode[STIX]{x1D6FC}\leq \unicode[STIX]{x1D714}_{1}$ , are distinct.