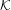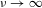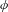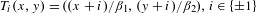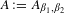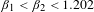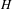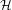Contents
Research Article
Asymptotic spectral gap and Weyl law for Ruelle resonances of open partially expanding maps
-
- Published online by Cambridge University Press:
- 07 October 2015, pp. 1-58
-
- Article
- Export citation
Non-archimedean connected Julia sets with branching
-
- Published online by Cambridge University Press:
- 12 October 2015, pp. 59-78
-
- Article
- Export citation
Multifractal analysis for weak Gibbs measures: from large deviations to irregular sets
-
- Published online by Cambridge University Press:
- 12 October 2015, pp. 79-102
-
- Article
- Export citation
Non-divergence of unipotent flows on quotients of rank-one semisimple groups
-
- Published online by Cambridge University Press:
- 28 December 2015, pp. 103-128
-
- Article
- Export citation
Measure evolution of cellular automata and of finitely anticipative transformations
-
- Published online by Cambridge University Press:
- 06 October 2015, pp. 129-145
-
- Article
- Export citation
Stretched-exponential mixing for
 $\mathscr{C}^{1+\unicode[STIX]{x1D6FC}}$ skew products with discontinuities
$\mathscr{C}^{1+\unicode[STIX]{x1D6FC}}$ skew products with discontinuities
-
- Published online by Cambridge University Press:
- 22 July 2015, pp. 146-175
-
- Article
- Export citation
Complex dynamics with focus on the real part
-
- Published online by Cambridge University Press:
- 21 July 2015, pp. 176-192
-
- Article
- Export citation
On a family of self-affine sets: Topology, uniqueness, simultaneous expansions
-
- Published online by Cambridge University Press:
- 27 November 2015, pp. 193-227
-
- Article
- Export citation
On the random dynamics of Volterra quadratic operators
-
- Published online by Cambridge University Press:
- 21 July 2015, pp. 228-243
-
- Article
- Export citation
Return- and hitting-time limits for rare events of null-recurrent Markov maps
-
- Published online by Cambridge University Press:
- 13 October 2015, pp. 244-276
-
- Article
- Export citation
Hausdorff spectrum of harmonic measure
-
- Published online by Cambridge University Press:
- 21 July 2015, pp. 277-307
-
- Article
- Export citation
Commutator criteria for strong mixing
-
- Published online by Cambridge University Press:
- 21 July 2015, pp. 308-323
-
- Article
- Export citation
Dynamical decompositions of
 $\unicode[STIX]{x1D6FD}X\setminus X$
$\unicode[STIX]{x1D6FD}X\setminus X$
-
- Published online by Cambridge University Press:
- 22 July 2015, pp. 324-336
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 37 Issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 03 January 2017, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
ETS volume 37 Issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 03 January 2017, pp. b1-b2
-
- Article
-
- You have access
- Export citation