Article contents
Homomorphisms between diffeomorphism groups
Published online by Cambridge University Press: 04 July 2013
Abstract
For 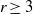 $r\geq 3$,
$r\geq 3$, 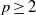 $p\geq 2$, we classify all actions of the groups
$p\geq 2$, we classify all actions of the groups 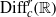 ${ \mathrm{Diff} }_{c}^{r} ( \mathbb{R} )$ and
${ \mathrm{Diff} }_{c}^{r} ( \mathbb{R} )$ and 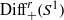 ${ \mathrm{Diff} }_{+ }^{r} ({S}^{1} )$ by
${ \mathrm{Diff} }_{+ }^{r} ({S}^{1} )$ by 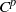 ${C}^{p} $-diffeomorphisms on the line and on the circle. This is the same as describing all non-trivial group homomorphisms between groups of compactly supported diffeomorphisms on 1-manifolds. We show that all such actions have an elementary form, which we call topologically diagonal. As an application, we answer a question of Ghys in the 1-manifold case: if
${C}^{p} $-diffeomorphisms on the line and on the circle. This is the same as describing all non-trivial group homomorphisms between groups of compactly supported diffeomorphisms on 1-manifolds. We show that all such actions have an elementary form, which we call topologically diagonal. As an application, we answer a question of Ghys in the 1-manifold case: if 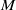 $M$ is any closed manifold, and
$M$ is any closed manifold, and 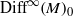 ${\mathrm{Diff} }^{\infty } \hspace{-2.0pt} \mathop{(M)}\nolimits_{0} $ injects into the diffeomorphism group of a 1-manifold, must
${\mathrm{Diff} }^{\infty } \hspace{-2.0pt} \mathop{(M)}\nolimits_{0} $ injects into the diffeomorphism group of a 1-manifold, must 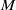 $M$ be one-dimensional? We show that the answer is yes, even under more general conditions. Several lemmas on subgroups of diffeomorphism groups are of independent interest, including results on commuting subgroups and flows.
$M$ be one-dimensional? We show that the answer is yes, even under more general conditions. Several lemmas on subgroups of diffeomorphism groups are of independent interest, including results on commuting subgroups and flows.
Information
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press, 2013
References
- 5
- Cited by

