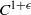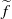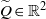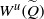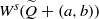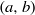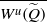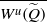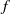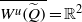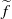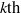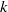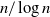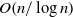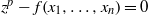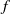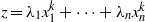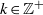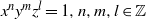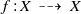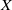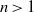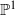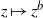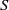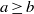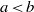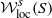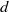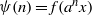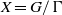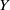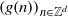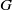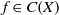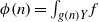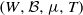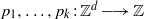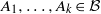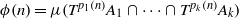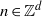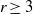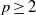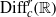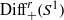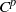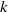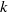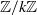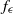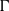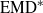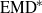Contents
Research Article
Area-preserving diffeomorphisms of the torus whose rotation sets have non-empty interior
-
- Published online by Cambridge University Press:
- 13 August 2013, pp. 1-33
-
- Article
- Export citation
Topological and algebraic reducibility for patterns on trees
-
- Published online by Cambridge University Press:
- 13 August 2013, pp. 34-63
-
- Article
- Export citation
Statistics and compression of scl
-
- Published online by Cambridge University Press:
- 17 January 2014, pp. 64-110
-
- Article
- Export citation
Integrability conditions of geodesic flow on homogeneous Monge manifolds
-
- Published online by Cambridge University Press:
- 30 September 2013, pp. 111-127
-
- Article
- Export citation
Weak limits of powers of Chacon’s automorphism
-
- Published online by Cambridge University Press:
- 27 September 2013, pp. 128-141
-
- Article
- Export citation
Abelian maximal pattern complexity of words
-
- Published online by Cambridge University Press:
- 13 August 2013, pp. 142-151
-
- Article
- Export citation
Superstable manifolds of invariant circles and codimension-one Böttcher functions
-
- Published online by Cambridge University Press:
- 05 July 2013, pp. 152-175
-
- Article
- Export citation
Nilsequences, null-sequences, and multiple correlation sequences
-
- Published online by Cambridge University Press:
- 28 June 2013, pp. 176-191
-
- Article
- Export citation
Homomorphisms between diffeomorphism groups
-
- Published online by Cambridge University Press:
- 04 July 2013, pp. 192-214
-
- Article
- Export citation
A dichotomy theorem for minimizers of monotone recurrence relations
-
- Published online by Cambridge University Press:
- 27 September 2013, pp. 215-248
-
- Article
- Export citation
Sharp large deviations for some hyperbolic systems
-
- Published online by Cambridge University Press:
- 13 August 2013, pp. 249-273
-
- Article
- Export citation
Analytic moduli for unfoldings of germs of generic analytic diffeomorphisms with a codimension
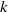 $k$ parabolic point
$k$ parabolic point
-
- Published online by Cambridge University Press:
- 28 June 2013, pp. 274-292
-
- Article
-
- You have access
- Open access
- Export citation
Weak equivalence and non-classifiability of measure preserving actions
-
- Published online by Cambridge University Press:
- 13 August 2013, pp. 293-336
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 35 Issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 31 December 2014, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
ETS volume 35 Issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 31 December 2014, pp. b1-b2
-
- Article
-
- You have access
- Export citation