No CrossRef data available.
Article contents
Instability of the isolated spectrum for W-shaped maps
Published online by Cambridge University Press: 30 May 2012
Abstract
In this note we consider the W-shaped map 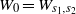 $W_0=W_{s_1,s_2}$ with
$W_0=W_{s_1,s_2}$ with 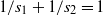 ${1}/{s_1}+{1}/{s_2}=1$ and show that the eigenvalue
${1}/{s_1}+{1}/{s_2}=1$ and show that the eigenvalue 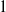 $1$ is not stable. We do this in a constructive way. For each perturbing map
$1$ is not stable. We do this in a constructive way. For each perturbing map 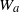 $W_a$ we show the existence of a ‘second’ eigenvalue
$W_a$ we show the existence of a ‘second’ eigenvalue 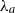 $\lambda _a$, such that
$\lambda _a$, such that 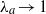 $\lambda _a\to 1$ as
$\lambda _a\to 1$ as 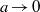 $a\to 0$, which proves instability of the isolated spectrum of
$a\to 0$, which proves instability of the isolated spectrum of 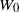 $W_0$. At the same time, the existence of second eigenvalues close to 1 causes the maps
$W_0$. At the same time, the existence of second eigenvalues close to 1 causes the maps 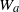 $W_a$to behave in a metastable way. There are two almost-invariant sets, and the system spends long periods of consecutive iterations in each of them, with infrequent jumps from one to the other.
$W_a$to behave in a metastable way. There are two almost-invariant sets, and the system spends long periods of consecutive iterations in each of them, with infrequent jumps from one to the other.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © 2012 Cambridge University Press
References
[1]Boyarsky, A. and Góra, P.. Laws of Chaos: Invariant Measures and Dynamical Systems in One Dimension (Probability and its Applications). Birkhäuser, Boston, MA, 1997.Google Scholar
[2]Eslami, P. and Góra, P.. Stronger Lasota–Yorke inequality for piecewise monotonic transformations. Preprint, available at http://www.peymaneslami.com/EslamiGora_Stronger_LY_Ineq.pdf.Google Scholar
[3]Eslami, P. and Misiurewicz, M.. Singular limits of absolutely continuous invariant measures for families of transitive maps. J. Difference Equ. Appl. 18 (2012), 739–750.Google Scholar
[4]Froyland, G. and Stančević, O.. Escape rates and Perron–Frobenius operators: open and closed dynamical systems. Discrete Contin. Dyn. Syst. Ser. B 14 (2010), 457–472.Google Scholar
[5]Keller, G.. Stochastic stability in some chaotic dynamical systems. Monatsh. Math. 94(4) (1982), 313–333.Google Scholar
[6]Keller, G. and Liverani, C.. Stability of the spectrum for transfer operators. Ann. Sc. Norm. Super. Pisa Cl. Sci. (4) 28(1) (1999), 141–152.Google Scholar
[7]Lasota, A. and Yorke, J. A.. On the existence of invariant measures for piecewise monotonic transformations. Trans. Amer. Math. Soc. 186 (1973), 481–488.Google Scholar
[8]Li, Z., Góra, P., Boyarsky, A., Proppe, H. and Eslami, P.. Family of piecewise expanding maps having singular measure as a limit of ACIMs, Ergod. Th. & Dynam. Sys. to appear.Google Scholar
[9]Li, Z..  $W$-like maps with various instabilities of acim’s. Preprint, 2011, arXiv:1109.5199v1.Google Scholar
$W$-like maps with various instabilities of acim’s. Preprint, 2011, arXiv:1109.5199v1.Google Scholar

