Hostname: page-component-7dd5485656-wxk4p Total loading time: 0 Render date: 2025-10-31T21:55:18.819Z Has data issue: false hasContentIssue false
  • English
  • Français

On a family of self-affine sets: Topology, uniqueness, simultaneous expansions

Published online by Cambridge University Press:  27 November 2015

KEVIN G. HARE  and
NIKITA SIDOROV
KEVIN G. HARE
Affiliation:
Department of Pure Mathematics, University of Waterloo, Waterloo, Ontario, Canada N2L 3G1 email kghare@uwaterloo.ca
NIKITA SIDOROV
Affiliation:
School of Mathematics, The University of Manchester, Oxford Road, Manchester M13 9PL, UK email sidorov@manchester.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

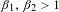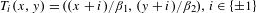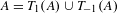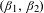Let $\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{2}>1$ and $T_{i}(x,y)=((x+i)/\unicode[STIX]{x1D6FD}_{1},(y+i)/\unicode[STIX]{x1D6FD}_{2}),i\in \{\pm 1\}$ . Let $A:=A_{\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{2}}$ be the unique compact set satisfying $A=T_{1}(A)\cup T_{-1}(A)$ . In this paper, we give a detailed analysis of $A$ and the parameters $(\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{2})$ where $A$ satisfies various topological properties. In particular, we show that if 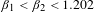$\unicode[STIX]{x1D6FD}_{1}<\unicode[STIX]{x1D6FD}_{2}<1.202$ , then $A$ has a non-empty interior, thus significantly improving the bound from Dajani et al [Self-affine sets with positive Lebesgue measure. Indag. Math. (N.S.)25 (2014), 774–784]. In the opposite direction, we prove that the connectedness locus for this family studied in Solomyak [Connectedness locus for pairs of affine maps and zeros of power series. Preprint, 2014, arXiv:1407.2563] is not simply connected. We prove that the set of points of $A$ which have a unique address has positive Hausdorff dimension for all 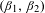$(\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{2})$ . Finally, we investigate simultaneous 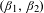$(\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{2})$ -expansions of reals, which were the initial motivation for studying this family in Güntürk [Simultaneous and hybrid beta-encodings. Information Sciences and Systems, 2008. CISS 2008. 42nd Annual Conference 2008, pp. 743–748].

Information

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 1 , February 2017 , pp. 193 - 227
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bandt, C.. On the Mandelbrot set for pairs of linear maps. Nonlinearity 15 (2002), 1127–1147.CrossRefGoogle Scholar
Dajani, K., Jiang, K. and Kempton, T.. Self-affine sets with positive Lebesgue measure. Indag. Math. (N.S.) 25 (2014), 774–784.CrossRefGoogle Scholar
Feng, D.-J. and Sidorov, N.. Growth rate for beta-expansions. Monatsh. Math. 162 (2011), 41–60.CrossRefGoogle Scholar
Glendinning, P. and Sidorov, N.. Unique representations of real numbers in non-integer bases. Math. Res. Lett. 8 (2001), 535–543.CrossRefGoogle Scholar
Güntürk, C. S.. Simultaneous and hybrid beta-encodings. Information Sciences and Systems, 2008. CISS 2008. 42nd Annual Conference 2008, pp. 743–748.Google Scholar
Hare, K. G.. Home page, http://www.math.uwaterloo.ca/∼kghare/preprints.Google Scholar
Hata, M.. On the structure of self-similar sets. Japan J. Appl. Math. 2 (1985), 381–414.Google Scholar
Kempton, T.. Counting 𝛽-expansions and the absolute continuity of Bernoulli convolutions. Monatsh. Math. 171 (2013), 189–203.CrossRefGoogle Scholar
Komornik, V. and Pethö, A.. Common expansions in noninteger bases. Publ. Math. Debrecen 85 (2014), 489–501.Google Scholar
Komornik, V. and de Vries, M.. Unique expansions of real numbers. Adv. Math. 221 (2009), 390–427.Google Scholar
Odlyzko, A. M. and Poonen, B.. Zeros of polynomials with 0, 1 coefficients. Enseign. Math. 39 (1993), 317–348.Google Scholar
Sidorov, N.. Almost every number has a continuum of beta-expansions. Amer. Math. Monthly 110 (2003), 838–842.Google Scholar
Sidorov, N.. Arithmetic dynamics. Topics in Dynamics and Ergodic Theory (London Mathematical Society Lecture Notes Series, 310) . Cambridge University Press, Cambridge, 2003, pp. 145–189.Google Scholar
Sidorov, N.. Combinatorics of linear iterated function systems with overlaps. Nonlinearity 20 (2007), 1299–1312.Google Scholar
Solomyak, B.. Connectedness locus for pairs of affine maps and zeros of power series. Preprint, 2014,arXiv:1407.2563. J. Fractal Geom. to appear.CrossRefGoogle Scholar