Quasidiagonals in strata of translation surfaces

Abstract

We classify quasidiagonals of the $SL(2, R)$ action on products of strata or hyperelliptic loci. We use the technique of diamonds developed by Apisa and Wright in order to use induction on this problem.

1. Introduction

For $\mathcal {H}$ a component of a stratum of the moduli space of translation surfaces, there is an $\operatorname {\mathrm {GL}}^+(2,\mathbb {R})$ -action on $\mathcal {H}$ . The breakthrough work of Eskin, Mirzakhani, and Mohammadi in [EM18, EMM15] showed that $\operatorname {\mathrm {GL}}^+(2,\mathbb {R})$ orbit closures of translation surfaces are varieties that are cut out by linear equations in period coordinates. For a multi-component stratum $\mathcal {H}_1\times \cdots \times \mathcal {H}_n$ , we have a diagonal $\operatorname {\mathrm {GL}}^+(2,\mathbb {R})$ action.

Definition 1.1. Let $\mathcal {H} = \mathcal {H}_1\times \cdots \times \mathcal {H}_n$ be a product of connected components of strata of translation surfaces. A multi-component invariant subvariety is a closed $\operatorname {\mathrm {GL}}^+(2,\mathbb {R})$ -invariant variety $\mathcal {L}\subset {\mathcal {H}}$ that is cut out by linear equations with real coefficients in period coordinate charts. An invariant subvariety is single-component if $n=1$ . Invariant subvarieties should be assumed to be single-component unless specified as multi-component. The term invariant subvariety includes whole strata.

Definition 1.2. A multi-component invariant subvariety $\mathcal {M}\subset \mathcal {H}_1 \times \cdots \times \mathcal {H}_n$ is called decomposable if up to reordering the $\mathcal {H}_i$ , there are multi-component invariant subvarieties $\mathcal {M}_1 \subset \mathcal {H}_1 \times \cdots \times \mathcal {H}_k$ , $\mathcal {M}_2 \subset \mathcal {H}_{k+1} \times \cdots \times \mathcal {H}_n$ such that $\mathcal {M} = \mathcal {M}_1\times \mathcal {M}_2$ . Here, $\mathcal {M}$ is prime if it is not decomposable.

One source of these multi-component invariant subvarieties comes from the WYSIWYG boundary of Mirzakhani and Wright [MW17]. Starting with a stratum of single-component translation surfaces, going to the boundary may produce multi-component surfaces. Chen and Wright proved in [CW21, Theorem 1.2] that the boundary of invariant subvarieties are multi-component invariant subvarieties.

Lemma 1.3. Let $\mathcal {M}$ be an invariant subvariety. Then, the diagonal in $\mathcal {M}\times \mathcal {M}$ defined as

$$ \begin{align*} \mathcal{D}:=\{(M,M)\in \mathcal{M} \times \mathcal{M} : M\in \mathcal{M}\} \end{align*} $$

is an invariant subvariety. The antidiagonal defined as

$$ \begin{align*} \overline{\mathcal{D}}:=\{(M,{-}\!\operatorname{\mathrm{Id}}(M))\in \mathcal{M}\times \mathcal{M}:M\in \mathcal{M}\} \end{align*} $$

is also an invariant subvariety.

Proof. Here, $\mathcal {D}$ is $GL^+(2,\mathbb {R})$ -invariant since the action is the diagonal action. Let $a_1,\ldots ,a_n$ be periods of the first surface and $b_1,\ldots ,b_n$ be the periods of the same saddles on the second surface. Then, $a_i=b_i$ are equations that cut out $\mathcal {D}$ . The proof for $\overline {\mathcal {D}}$ is similar.

Remark 1.4. In hyperelliptic strata, the diagonal and antidiagonal are the same.

We generalize the above examples in the following definition.

Definition 1.5. Let $\mathcal {M}_1, \mathcal {M}_2$ be invariant subvarieties. A prime invariant subvariety $\Delta $ is a quasidiagonal in $\mathcal {M}_1\times \mathcal {M}_2$ if the projection maps $p_i:\Delta \to \mathcal {M}_i$ are dominant. We allow $\dim \Delta> \dim \mathcal {M}_i$ . As a shorthand, we will write ‘ $\Delta \subset \mathcal {M}_1\times \mathcal {M}_2$ is a quasidiagonal’. By Proposition 2.4 and Remark 2.5 below, every quasidiagonal has a corresponding quasidiagonal where both sides have equal area. Thus, we will assume throughout the paper that both components have equal area.

Remark 1.6. Any prime invariant subvariety $\Delta $ is a quasidiagonal in $\overline {p_1(\Delta )}\times \overline {p_2(\Delta )}$ .

Definition 1.7. Let X be a Riemann surface. A hyperelliptic involution j on X is an automorphism of X whose quotient is $\mathbb {P}^1$ . Let $(X,\omega )$ be a hyperelliptic translation surface if there exists a hyperelliptic involution $j:X\to X$ such that $j^*(\omega ) = -\omega $ . Let $\mathcal {H}$ be a component of a stratum of translation surfaces. The hyperelliptic locus in $\mathcal {H}$ is an invariant subvariety that consists of all hyperelliptic translation surfaces of $\mathcal {H}$ .

The following is the main theorem of the paper and proves a conjecture by Apisa and Wright [AW23b, Conjecture 8.35] in the case of Abelian differentials.

Theorem 1.8. Let $\mathcal {M}_i$ be either a connected component of a stratum of translation surfaces in genus $g \ge 2$ (without marked points) or the hyperelliptic locus in such a stratum for $i=1,2$ . The only (equal area) quasidiagonals $\Delta \subset \mathcal {M}_1\times \mathcal {M}_2$ are the diagonal and antidiagonal when $\mathcal {M}_1 = \mathcal {M}_2$ .

Example 1.9. We do not allow marked points because this will give rise to many uninteresting examples of quasidiagonals. For example, let $\Delta \subset \mathcal {M}_1\times \mathcal {M}_2$ be a quasidiagonal. Then, $\{((M_1,p),M_2):(M_1,M_2)\in \Delta , p\in M_1\}$ is a quasidiagonal in $\mathcal {M}_1^{*}\times \mathcal {M}_2$ . (Here, $\mathcal {M}_1^*$ denotes the invariant subvariety which is $\mathcal {M}_1$ along with a free marked point.)

Classifying quasidiagonals is helpful with inductive arguments that use the WYSIWYG boundary. In addition, this classification is interesting since quasidiagonals show relationships between $\mathcal {M}_1$ and $\mathcal {M}_2$ .

Definition 1.10. A continuous, $SL(2,\mathbb {R})$ -invariant map between invariant subvarieties ${\phi : \mathcal {M}\to \mathcal {N}}$ is called a morphism if it is linear in period coordinates.

A morphism $\phi :\mathcal {M}\to \mathcal {N}$ between invariant subvarieties gives a quasidiagonal $\{(M,\phi (M)): M\in \mathcal {M}\}\subset \mathcal {M}\times \overline {\phi (\mathcal {M})}$ . For example, when $\mathcal {H}$ is not hyperelliptic, ${-}{\mathrm {Id}}$ gives rise to a non-trivial automorphism of $\mathcal {H}$ . This corresponds to the antidiagonal.

Corollary 1.11. Let $\mathcal {H},\mathcal {H}'$ be strata. There are no dominant morphisms $\phi : \mathcal {H}\to \mathcal {H}'$ other than $\operatorname {\mathrm {Id}},{-}{\mathrm {Id}}:\mathcal {H}\to \mathcal {H}$ .

The above support the following heuristic: a quasidiagonal $\Delta \subset \mathcal {M}_1\times \mathcal {M}_2$ exists if and only if $\mathcal {M}_1$ and $\mathcal {M}_2$ are ‘related’.

Example 1.12. Let $\widetilde {\mathcal {H}}(2,0^2) \subset \mathcal {H}(2^2,1^2)$ be the space of all double covers of surfaces in $\mathcal {H}(2)$ branched at two marked points. There is a quasidiagonal $\Delta \subset \mathcal {H}(2)\times \widetilde {\mathcal {H}}(2,0^2)$ consisting of all $(M,\widetilde M)$ , where $\widetilde M$ is a branched double cover of M.

Lemma 1.13. Given quasidiagonals $ \Delta _L \subset \mathcal {M}_1\times \mathcal {M}_2$ and $\Delta _R \subset \mathcal {M}_2\times \mathcal {M}_3$ , then ${\Delta _L * \Delta _R \subset \mathcal {M}_1\times \mathcal {M}_3}$ defined as $\{(M_1,M_3)\in \mathcal {M}_1\times \mathcal {M}_3:\text { there exists } M_2 \text { such that} (M_1,M_2)\in \Delta _L,(M_2,M_3)\in \Delta _R\}$ is a quasidiagonal.

Proof. Here, $\Delta _L*\Delta _R$ is prime since the absolute periods of each side determines the absolute periods of the other. Additionally, $p_2(\Delta _L)\cap p_1(\Delta _R)$ is a Zariski open subset of $\mathcal {M}_2$ . Furthermore, $p_1: \Delta _L*{\Delta _R\to \mathcal {M}_1}$ is dominant since $p_1(\Delta _L\times \Delta _R) = p_1(p_2^{-1}(p_2(\Delta _L)\cap p_1(\Delta _R)))$ .

Corollary 1.14. Let $\mathcal {M}_1,\mathcal {M}_2$ be invariant subvarieties. We define $\mathcal {M}_1\sim \mathcal {M}_2$ if there exists a quasidiagonal $\Delta \in \mathcal {M}_1\times \mathcal {M}_2$ . Then, $\sim $ is an equivalence relation.

Corollary 1.14 follows from Lemma 1.13. Theorem 1.8 implies that there are many distinct $\sim $ equivalence classes. It would be interesting to classify these equivalence classes.

Another application of this work is to measurable joinings of Masur–Veech measures.

Definition 1.15. Let $(X_1, \mu _1, T_1)$ and $(X_2, \mu _2, T_2)$ , where $\mu _i$ is a measure on a space $X_i$ and $T_i:X_i\to X_i$ is a measure-preserving transformation. A joining is a measure on $X_1\times X_2$ invariant under the product transformation $T_1\times T_2$ , whose marginals on $X_i$ are $\mu _i$ . A measure $\mu $ on a space X is prime if it cannot be written as a product $\mu = \mu _1\times \mu _2$ , $X = X_1\times X_2$ , where $\mu _i$ is a measure on $X_i$ .

Assuming a multi-component version of Eskin and Mirzakhani’s measure classification result, Theorem 1.8 classifies ergodic measurable joinings of Masur–Veech measures on strata.

Assumption 1.16. (See [MW17, Conjecture 2.10]) We define an affine measure as in [EM18, Definition 1.1]. For a multi-component stratum under the diagonal action of $\operatorname {\mathrm {SL}}(2,\mathbb {R})$ , the only ergodic invariant measures are $\operatorname {\mathrm {SL}}(2,\mathbb {R})$ -invariant and affine.

Corollary 1.17. Let $\mathcal {M}_i$ be either a stratum of translation surfaces or the hyperelliptic locus in such a stratum and $\mu _i$ be the Masur–Veech measure on the unit area locus of $\mathcal {M}_i$ for $i=1,2$ . Under Assumption 1.16, the only prime ergodic joinings of $\mu _1,\mu _2$ (under the diagonal action of $\operatorname {\mathrm {SL}}(2,\mathbb {R})$ ) are the Masur–Veech measure on the diagonal or antidiagonal.

Proof. By Assumption 1.16, the only ergodic $\operatorname {\mathrm {SL}}(2,\mathbb {R})$ -invariant measures are affine, so they are supported on an affine subvariety $\mathcal {M}$ . Since the joining is prime, $\mathcal {M}$ must be prime. The condition on the marginals implies that $\mathcal {M}$ must be a quasidiagonal in ${\mathcal {M}_1\times \mathcal {M}_2}$ . Our assumptions also guarantee equal area on both sides. We may now apply Theorem 1.8.

1.1. Organization

Section 2 quickly summarizes the techniques used in the proof of the main theorem. The proof will use induction. Section 3, which is slightly technical, is the base case of the proof. The heart of the proof is in §4, which is quite short.

2. Background

In this section, we define notation and terminology, and list the background needed in the paper. We also prove the results needed in the proof of the main theorem. By ‘stratum’, we will refer to a ‘connected component of a stratum of connected translation surfaces without marked points in genus at least $2$ ’ unless otherwise stated. Let $\mathcal {H}$ be a stratum. We will often use a single letter $M = (X,\omega )\in \mathcal {H}$ to denote a translation surface, where X is the underlying Riemann surface and $\omega $ the holomorphic $1$ -form.

2.1. Prime invariant subvarieties

The notion of a prime invariant subvariety (Definition 1.2) was defined and studied in [CW21]. Here, we list some results about them.

Theorem 2.1. (Chen and Wright [CW21, Theorem 1.3])

Let $\mathcal {M}\subset \mathcal {H}_1\times \cdots \times \mathcal {H}_n$ be a prime invariant subvariety, where $\mathcal {H}_i$ is a stratum of translation surfaces of genus $g_i$ . Let $p_i$ be the map and $p_i:\mathcal {M}\to H^1(S_{g_i})$ be the projection of $\mathcal {M}$ on $\mathcal {H}_i$ followed by the absolute period map. Then, all $g_i$ are equal and for any $i,j$ , there is an invertible linear map $A_{ij}:H^1(S_{g_i}) \to H^1(S_{g_j})$ such that $A_{ij} \circ p_i = p_j$ . In particular, each component must have the same rank. We will say that the absolute periods of $\mathcal {M}$ determine each other to refer to this property.

Definition 2.2. Let $\mathcal {M}$ be a (single-component) invariant subvariety, and $M\in \mathcal {M}$ . Let $p:H^1(M,\Sigma ;\mathbb {C})\to H^1(M;\mathbb {C})$ be the forgetful map. The rank of $\mathcal {M}$ is $\tfrac 12\dim p(T_M\mathcal {M})$ . The rank of a prime invariant subvariety $\mathcal {N}$ is $\operatorname {\mathrm {rk}} \overline {p_i(\mathcal {N})}$ , which is independent of i by Theorem 2.1.

Remark 2.3. By [AEM17, Theorem 1.4], $p(T_M \mathcal {M})$ is symplectic, so the rank of an invariant subvariety is always an integer.

Proposition 2.4. (Chen and Wright [CW21, Corollary 7.4])

In a prime invariant subvariety, the $g_t$ action is ergodic on the unit area locus. Thus, the ratio of areas of the components is constant.

Remark 2.5. For any quasidiagonal $\Delta $ , we get an infinite number of quasidiagonals ${\Delta _r = \{(M_1,rM_2):(M_1,M_2)\in \Delta \}}$ . Thus, we can scale $\Delta $ so that both components have the same area.

2.2. Cylinder deformations

By a cylinder C, we refer to a maximal topological open annulus foliated by closed geodesics. If C is a cylinder on M, there is a corresponding cylinder on every surface in a small enough neighborhood of M. As an abuse of notation, we often refer to these corresponding cylinders as C. By core curve of a cylinder, we refer to one of these closed geodesics. A cylinder has two boundary components, which may overlap. Since cylinders are maximal, there is always at least one singularity on each boundary component, and a cylinder is simple if each boundary component only contains a single singularity. A cross curve is a saddle connection contained in C that goes from one boundary component to the other.

Let $\mathcal {M} \subset \mathcal {H} = \mathcal {H}_1\times \cdots \times \mathcal {H}_n$ be a multi-component invariant subvariety. Let ${\mathcal {C} = \{C_1,\ldots ,C_r\}}$ be a collection of cylinders on $M = (M_1,\ldots ,M_n)\in \mathcal {M}$ and let $\gamma _i$ be the core curve of $C_i$ . The tangent space $T_M\mathcal {M}$ is a subspace of $T_M\mathcal {H} = H^1(M,\Sigma ;\mathbb {C}) := H^1(M_1,\Sigma ;\mathbb {C})\times \cdots \times H^1(M_n,\Sigma ;\mathbb {C})$ . Thus, there is a projection $\pi :H_1(M,\Sigma ;\mathbb {C})\to (T_M\mathcal {M})^*$ . We view $\gamma _i$ as elements of $H_1(M,\Sigma ;\mathbb {C})$ by setting the $H_1(M_j,\Sigma ;\mathbb {C})$ to be zero on the components $M_j$ that do not contain $C_i$ .

Definition 2.6. Here, $\mathcal {C}$ is called $\mathcal {M}$ -parallel if all $\pi (\gamma _i)$ are colinear in $(T_M\mathcal {M})^*$ . Being $\mathcal {M}$ -parallel is an equivalence relation on cylinders, so we call $\mathcal {C}$ an $\mathcal {M}$ -parallel class if it is an equivalence class of $\mathcal {M}$ -parallel cylinders.

Intuitively, $\mathcal {M}$ -parallel means that there is a neighborhood $M\in U \subset \mathcal {M}$ such that all cylinders in $\mathcal {C}$ remain parallel in this neighborhood. See [Wri15] for a more detailed discussion on $\mathcal {M}$ -parallel cylinders.

We will sketch a proof of Wright’s cylinder deformation theorem [Wri15] for multi-component strata. The proof is identical to the original proof, but we omit many details. Let $\mathcal {H} = \mathcal {H}_1 \times \cdots \times \mathcal {H}_n$ be a multi-component stratum. First, we reproduce a theorem by Smillie and Weiss [SW04, Theorem 5] that will be used in the proof. The original theorem was only stated for single-component strata but the proof in the multi-component case is identical. Let $U = \{ (\!\begin {smallmatrix} 1 & t \\ 0 & 1 \end {smallmatrix}\!) : t\in \mathbb {R} \} \subset \operatorname {\mathrm {SL}}(2,\mathbb {R})$ .

Theorem 2.7. (Smillie and Weiss) [SW04]

Every U orbit closure contains a horizontally periodic surface.

Lemma 2.8. Let $M=(M_1,\ldots ,M_n)\in \Delta $ be a prime invariant subvariety. Choose a period coordinate chart U around M and let $M^t=(M_1^t,\ldots ,M_n^t)$ , $t\in [0,1]$ , be a path in U with $M^0=M$ . If for some i, for each t, the imaginary parts of the absolute periods of $M^t_i$ are the same, then the same is true for all i.

Proof. By Theorem 2.1, the absolute periods of $M_i$ determine each other and $\mathcal {M}$ is cut out by equations with real coefficients in period coordinate charts.

Lemma 2.9. Let $M=(M_1,M_2) \in \mathcal {M} $ be a two-component prime invariant subvariety. If $M_1$ is horizontally periodic, then $M_2$ must be horizontally periodic. In this case, we say that M is horizontally periodic.

Proof. By Theorem 2.7, there exists a sequence $t_n\to \infty $ such that $ (\!\begin {smallmatrix} 1 & t_n\\ 0 & 1 \end {smallmatrix}\!)(M_1,M_2) \to (M_1^{\infty }, M_2^{\infty })$ . Let $(U_1,U_2)$ be a neighborhood around $(M_1^{\infty }, M_2^{\infty })$ in period coordinates. For large enough $t_n$ , $M^{t_n}_1 := (\!\begin {smallmatrix} 1 & t_n\\ 0 & 1 \end {smallmatrix}\!)M_1 \in U_1$ and since $M^{t_n}_1$ and $M^\infty _1$ all lie on T, they all have the same real periods. Assume by contradiction that $M_2$ was not horizontally periodic. Then, for large enough n, there is a surface $M_2^{t_n} := (\!\begin {smallmatrix} 1 & t_n\\ 0 & 1 \end {smallmatrix}\!)M_2$ such that there is some cylinder C of $M^\infty _2$ that persists on $M^{t_n}_2$ , but it is not horizontal. Thus, the core curve of C is an absolute period that changes in imaginary part on a path from $M^{t_n}_2$ to $M_2^\infty $ . This contradicts Lemma 2.8.

Now, we continue to the statement of the cylinder deformation theorem. Let $\mathcal {C}$ consist of cylinders $C_1,\ldots ,C_r$ , with heights $h_1,\ldots ,h_r$ , and let $\alpha _i$ be the cohomology class associated to the core curve of $C_i$ under Poincaré duality $H_1(M-\Sigma ;\mathbb {C})\cong H^1(M,\Sigma ;\mathbb {C})$ . Define

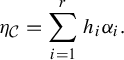$$ \begin{align*} \eta_{\mathcal{C}} = \sum_{i=1}^r h_i\alpha_i. \end{align*} $$

See also [Wri15, §2] for a more detailed definition of $\eta _{\mathcal {C}}$ . For horizontal cylinders, moving in the direction of $i\eta _{\mathcal {C}}$ in period coordinates stretches all the cylinders in $\mathcal {C}$ (in proportion to the height of the cylinder) and does not change the rest of the surface. Moving in the direction of $\eta _{\mathcal {C}}$ shears all the cylinders of $\mathcal {C}$ and does not change the rest of the surface. We are now able to state the theorem.

Theorem 2.10. (Cylinder deformation theorem [Wri15])

Let $\mathcal {M} \subset \mathcal {H}$ be an invariant subvariety of a multi-component stratum. Let $\mathcal {C}$ be an $\mathcal {M}$ -parallel class of cylinders on M. Then, $\eta _{\mathcal {C}} \in T_{M}\mathcal {M}$ . (Here, $T_M\mathcal {M}$ denotes the tangent space to $\mathcal {M}$ at M, which is a subspace of $H^1(M, \Sigma ;\mathbb {C})$ ).

The following lemma is [Wri15, Lemma 3.1].

Lemma 2.11. Let M be horizontally periodic and $\mathcal {C}$ be an $\mathcal {M}$ -parallel class of cylinders. Let the moduli of the cylinders of $\mathcal {C}$ be independent over $\mathbb {Q}$ of the moduli of the remaining horizontal cylinders. Then, $\eta _{\mathcal {C}}\in T_M\mathcal {M}$ .

Proof. The U-flow of a horizontally periodic surface is the same as the flow on an r-dimensional torus whose slope is determined by the moduli of the cylinders.

The following lemma can be found in [Wri15, Lemma 4.9].

Lemma 2.12. Let V be a finite-dimensional vector space and $F\subset V^*$ a finite collections of linear functionals on V, no two of which are colinear. The collection of functions $1/w$ for $w\in F$ are linearly independent over $\mathbb {R}$ . This remains true when the functions are restricted to any non-empty open set of V.

Proof of Theorem 2.10

Let $\mathcal {C}$ be an $\mathcal {M}$ -parallel class of cylinders on M. By Theorem 2.7, there is a horizontally periodic surface $M'$ in the U orbit closure of M. The corresponding set of cylinders, which we still call $\mathcal {C}$ , is an $\mathcal {M}$ -parallel class on $M'$ .

Claim 2.13. There is a surface $M"$ that is a real deformation of $M'$ such that the moduli of the cylinders in $\mathcal {C}$ are independent over $\mathbb {Q}$ of the moduli of the cylinders not in $\mathcal {C}$ [Wri15, Lemma 4.10].

By the claim, we have a surface $M"$ where the moduli of the cylinders in $\mathcal {C}$ are independent of the rest of the cylinders. Lemma 2.11 finishes the proof. Thus, it suffices to prove the claim. Let $C_{r+1},\ldots ,C_l$ be the cylinders of $M'$ not in $\mathcal {C}$ , and let $m_i$ be the moduli of the cylinder $C_i$ . Assume by contradiction that the claim is false. Because $\mathcal {M}$ is cut out by real linear equations in period coordinates, there is some rational relation that holds for small real deformations of $M'$ ,

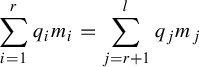$$ \begin{align*} \sum_{i=1}^r q_im_i = \sum_{j=r+1}^{l} q_jm_j \end{align*} $$

for some $q_i\in \mathbb {Q}$ , where neither the right-hand nor the left-hand side is identically zero. Recall that $m_i = h_i/c_i$ is the modulus of a cylinder. Since the cylinders in $\mathcal {C}$ are all $\mathcal {M}$ -parallel, the $c_i$ are all multiples of each other in a small neighborhood. Allowing the coefficients to be real numbers, we can remove all but one representative from each $\mathcal {M}$ -parallel class. Thus, we have an equation of the form

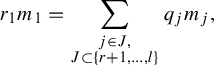$$ \begin{align*} r_1m_1 = \sum_{\substack{j\in J, \\ J\subset \{r+1,\ldots,l\}}} q_jm_j, \end{align*} $$

where neither side is zero and no two of the cylinders $C_{j}$ are $\mathcal {M}$ -parallel. However, $1/m_{i_j}$ are linear functional (over an open set in the space of real deformations) that are not colinear, so this relation cannot hold by Lemma 2.12. This is a contradiction, so the claim and the theorem are proven.

The following corollary, which is [NW14, Proposition 3.2], immediately generalizes to the multi-component setting.

Corollary 2.14. Let M be a surface in a multi-component invariant subvariety $\mathcal {M}$ . Let $\mathcal {C},\mathcal {C}'$ be $\mathcal {M}$ -parallel classes of cylinders on M, and let $C,D$ be cylinders in $\mathcal {C}'$ . Then,

$$ \begin{align*} \frac{\operatorname{\mathrm{area}}(C\cap \mathcal{C})}{\operatorname{\mathrm{area}}(C)} = \frac{\operatorname{\mathrm{area}}(D\cap \mathcal{C})}{\operatorname{\mathrm{area}}(D)}.\end{align*} $$

Lemma 2.15. Let $\mathcal {M}$ be a prime invariant subvariety and $\mathcal {C}$ be a $\mathcal {M}$ -parallel class of cylinders on a surface $M=(M_1,\ldots ,M_n)\in \mathcal {M}$ . Define $\mathcal {M}_i := \overline {p_i(\mathcal {M})}$ to be the closure of the ith projection of $\mathcal {M}$ . Let $\mathcal {C}_i$ be the cylinders of $\mathcal {C}$ on $M_i$ . Then, $\mathcal {C}_i$ is a non-empty $\mathcal {M}_i$ -parallel class of cylinders.

Proof. First, we show each $\mathcal {C}_i$ is non-empty. Assume by contradiction that $M_i$ does not have a cylinder in $\mathcal {C}$ , but $M_j$ does. By the cylinder deformation theorem, we can perform standard cylinder dilation on $\mathcal {C}$ while remaining in $\Delta $ . This causes the absolute periods of $M_j$ to change without changing the absolute periods of $M_i$ , which contradicts Theorem 2.1.

Now we show that each $\mathcal {C}_i$ is an $\mathcal {M}_i$ -parallel class. Let $p:H^1(M,\Sigma ;\mathbb {C}) \to H^1(M;\mathbb {C}) $ be the projection from relative to absolute cohomology. Then, $(pT_M\mathcal {M})^*\subset (T_M\mathcal {M})^*$ . Since the core curves of cylinders $\gamma _i$ are elements of absolute homology $H_1(M;\mathbb {C})$ , we have $\pi (\gamma _i) \in (pT_M\mathcal {M})^*$ (where $\pi $ is defined in the discussion before Definition 2.6). Now, let $\{\gamma _j\}$ be the core curves of cylinders of $M_i$ . By [CW21, Theorem 1.3], $(pT_M\Delta )^* \cong (pT_{M_i}\mathcal {M}_i)^*$ , so $\pi (\gamma _i)$ are colinear in $(pT_{M_i}\mathcal {M}_i)^*$ if and only if they are colinear in $(pT_M\Delta )^*$ . Thus, $\gamma _i$ are $\mathcal {M}_i$ -parallel if and only if they are $\Delta $ -parallel.

2.3. WYSIWYG compactification

We give a short overview of the WYSIWYG compactification. See [CW21, MW17] for more formal introductions.

Definition 2.16. Let $\mathcal {H},\mathcal {H}'$ be strata of multi-component translation surfaces potentially having marked points. Let $M_n = (X_n,\omega _n)\in \mathcal {H}$ and $\Sigma _n$ be its set of singularities and marked points, and let $M = (X,\omega ) \in \mathcal {H}'$ and $\Sigma $ its set of singularities and marked points. We say that $M_n$ converges to M if there are decreasing neighborhoods $\Sigma \subset U_i \subset M$ such that there are $g_i: X-U_i\to X_i$ that are diffeomorphisms onto their images satisfying:

1. (1) $g_i^*(\omega _i) \to \omega $ in the compact-open topology on $M-\Sigma $ ;

2. (2) the injectivity radius of points not in the image of $g_i$ goes to zero uniformly in i.

See [MW17, Definition 2.2].

Thus, we can construct $\partial \mathcal {H}$ from $\mathcal {H}$ by including all $\mathcal {H}'$ such that a sequence of surfaces in $\mathcal {H}$ converges to a surface in $\mathcal {H}'$ . Multiple copies of a stratum can be included if there are two sequences that converge to the same surface in $\mathcal {H}'$ but are not close in $\mathcal {H}$ . We call the union $\overline {\mathcal {H}} = \mathcal {H} \cup \partial \mathcal {H}$ (with the topology given by the above convergence of sequences) the WYSIWYG partial compactification of $\mathcal {H}$ . For any invariant subvariety $\mathcal {M}\subset \mathcal {H}$ , we define $\partial M$ to be $\overline {\mathcal {M}}-\mathcal {M}$ , where the closure $\overline {\mathcal {M}}$ is taken in $\overline {\mathcal {H}}$ .

Remark 2.17. Even if $M_n$ is a convergent sequence of surfaces without marked points, its limit may have marked points.

Let $M_n = (X_n,\omega _n)\in \mathcal {M}$ be a sequence of multi-component translation surfaces that has a limit $M = (X,\omega ) \in \partial \mathcal {M}$ . Let $\mathcal {H}'$ be the stratum with marked points that contains M. Let $\mathcal {N}$ be the connected component of $\mathcal {H}'\cap \partial \mathcal {M}$ that contains M. We call $\mathcal {N}$ the component of the boundary of $\mathcal {M}$ that contains M. The sequence $X_n$ will approach a limit $X'$ in the Deligne–Mumford compactification. For large enough n, there is a map $f_n:X_n\to X'$ called the collapse map. There is also a map $g:X\to X'$ identifying together marked points of X. Define $(f_n)_*:H_1(X_n,\Sigma _n)\to H_1(X,\Sigma )$ and $V_n = \ker ((f_n)_*)$ .

Proposition 2.18. After identifying $H_1(X_n,\Sigma _n)$ for different n, $V_n$ eventually becomes constant which we call V. We call V the space of vanishing cycles. Here, $T_M\mathcal {H}'$ can be identified with $\operatorname {\mathrm {Ann}}(V)$ .

This proposition was proven for multi-component surfaces in [MW17, Propositions 2.5 and 2.6].

Theorem 2.19. (Mirzakhani and Wright [MW17], Chen and Wright [CW21])

Let $\mathcal {M}$ be an invariant variety in a stratum $\mathcal {H}$ of connected translation surfaces. Let $M_n\in \mathcal {M}$ be a sequence that converges to $M \in \partial M$ . Let $\mathcal {H}'$ be the stratum that contains M and $\mathcal {M}'$ be the component of the boundary of $\mathcal {M}$ that contains M. By Proposition 2.18, we identify $T_M\mathcal {H}'$ with $\operatorname {\mathrm {Ann}}(V)$ . Then, $T_M \mathcal {M}'$ can be identified with $T_{M_n}\mathcal {M} \cap \operatorname {\mathrm {Ann}}(V)$ . In particular, the codimension of $\mathcal {M}'$ in $\mathcal {M}$ is the dimension of the space of vanishing cycles, V.

This theorem was proven in [MW17, Theorem 1.1] when M is connected, and in [CW21, Theorem 1.2] when M is disconnected.

2.4. Cylinder collapse

We will define cylinders collapse and diamonds in a similar fashion to [AW23a, Lemma 4.9]. Let $ \mathcal {M}$ be an invariant subvariety of multi-component surfaces. Let $M\in \Delta $ and $\mathcal {C}$ be an $\mathcal {M}$ -parallel class of horizontal cylinders on M. Fix a cross curve $\gamma $ of some cylinder in $\mathcal {C}$ . We now define the operations $u_s^{\mathcal {C}}$ and $a_t^{\mathcal {C}}$ , which are shearing and scaling the cylinders $\mathcal {C}$ , respectively. Let $u_s^{\mathcal {C}}(M)$ be the surface obtained by adding $s\eta _{\mathcal {C}}$ to M in period coordinates, where $\eta _{\mathcal {C}}$ is defined in the paragraph above Theorem 2.10. Define $a_t^{\mathcal {C}}(M)$ to be the surface obtained by adding $(e^{t}-1)\sqrt {-1}\eta _{\mathcal {C}}$ to M in period coordinates. We define $\operatorname {\mathrm {Col}} _{\mathcal {C},\gamma } M$ to be the following operation. Choose s so that $\gamma $ is vertical on $u_s^{\mathcal {C}}(M)$ . Then,

$$ \begin{align*} \operatorname{\mathrm{Col}} _{\mathcal{C},\gamma} M : = \lim_{t\to -\infty} a_t^{\mathcal{C}}u_s^{\mathcal{C}}M. \end{align*} $$

This limit exists in the WYSIWYG compactification, see [MW17, Lemma 3.1] or [AW23a, Lemma 4.9]. We also define

$$ \begin{align*} \operatorname{\mathrm{Col}} _{\mathcal{C},\gamma}\mathcal{M} \end{align*} $$

to be the component of $\partial \mathcal {M}$ that contains $\operatorname {\mathrm {Col}} _{\mathcal {C},\gamma } M $ . If $\mathcal {C}_1,\mathcal {C}_2$ are disjoint equivalence classes of cylinders on M and $\gamma _1,\gamma _2$ are cross curves of cylinders of $\mathcal {C}_1,\mathcal {C}_2$ , respectively, we define

$$ \begin{align*} \operatorname{\mathrm{Col}}_{\mathcal{C}_1,\mathcal{C}_2,\gamma_1,\gamma_2}M = \operatorname{\mathrm{Col}}_{\mathcal{C}_1,\gamma_1}\operatorname{\mathrm{Col}} _{\mathcal{C}_2,\gamma_2}M = \operatorname{\mathrm{Col}}_{\mathcal{C}_2,\gamma_2}\operatorname{\mathrm{Col}}_{\mathcal{C}_1,\gamma_1}M. \end{align*} $$

Definition 2.20. Let $\mathcal {M}$ be a multi-component invariant subvariety. A surface $M\in \mathcal {M}$ is called $\mathcal {M}$ -generic if two saddles on the same component of M are parallel only if they are $\mathcal {M}$ -parallel. If $\mathcal {M}$ is clear from context, we will just call M generic.

Lemma 2.21. For any multi-component invariant subvariety, a dense $G_\delta $ set of surfaces are generic.

Proof. The condition where two saddles that are not generically parallel are parallel defines a linear subspace in period coordinates. There are countably many saddles on a surface, and the coefficients of the equation must be in the field of definition of the component on which the two saddles are. The field of definition is a finite extension of $\mathbb {Q}$ by [Wri14, Theorem 1.1].

Lemma 2.22. Let $\mathcal {M}$ be a stratum or hyperelliptic locus, and let $M\in \mathcal {M}$ be generic. Then, every cylinder C on $\mathcal {M}$ is simple.

Proof. Assume by contradiction there was a cylinder C that was not simple. Then, there would be a boundary component with more than one saddle. These saddles would be $\mathcal {M}$ -parallel because M is generic. That is not possible in a stratum, so $\mathcal {M}$ must be a hyperelliptic locus. Let $\gamma _1,\gamma _2$ be parallel saddles on the boundary of C. Every cylinder on M is either fixed or swapped with another cylinder. In either case, the quotient surface N has a corresponding cylinder, which we still call C, with two saddles, which we still call $\gamma _1$ and $\gamma _2$ . Now we appeal to [MZ08], and we will use the formulation and terminology of [AW21, Proposition 4.4]. By this theorem, removing $\gamma _1,\gamma _2$ from N disconnects the surface into two components $A, B$ , and the component B not containing C has trivial holonomy. Since $\mathcal {M}$ is hyperelliptic, N is genus $0$ , so B is topologically a cylinder. However, gluing this cylinder back along $\gamma _1,\gamma _2$ would create genus. This is a contradiction since N is genus $0$ . Thus, the cylinder $C \subset M$ must have been simple.

Lemma 2.23. Let $\mathcal {M}$ be a stratum or hyperelliptic locus. Let $M \in \mathcal {M}$ be generic, ${\mathcal {C}\subset M}$ be an $\mathcal {M}$ -parallel class and $\gamma $ a cross curve of $\mathcal {C}$ . Then, $\operatorname {\mathrm {Col}} _{\mathcal {C},\gamma }M$ is connected, and $\operatorname {\mathrm {Col}} _{\mathcal {C},\gamma }\mathcal {M}$ is codimension $1$ .

Proof. By Lemma 2.22, all the cylinders in $\mathcal {C}$ are simple. Collapsing a set of simple cylinders does not disconnect a translation surface. Now, we show $\dim \operatorname {\mathrm {Col}}_{\mathcal {C},\gamma }\mathcal {M} = \dim \mathcal {M} - 1$ . We note that after a standard shear of $\mathcal {C}$ , two saddles $\gamma _1,\gamma _2 \subset \mathcal {C}$ are parallel if and only if they were parallel in M. Thus, every curve that goes to zero in $\operatorname {\mathrm {Col}}_{\mathcal {C}, \gamma }M$ is $\mathcal {M}$ -parallel. The space of vanishing cycles is dimension $1$ when viewed as functionals on $T_M\mathcal {M}$ , so by Theorem 2.19, $\operatorname {\mathrm {Col}}_{\mathcal {C},\gamma }\mathcal {M}$ is dimension one lower than $\mathcal {M}$ .

Lemma 2.24. Let $\mathcal {M}$ be an invariant subvariety and $\mathcal {N} \subset \mathcal {M}$ be a codimension $1$ subvariety. Then, $\mathcal {M},\mathcal {N}$ must have the same rank.

Proof. Here, $p(T \mathcal {N})\subset p(T\mathcal {M})$ is codimension at most $1$ and the symplectic form on $p(T\mathcal {M})$ restricts to a symplectic form on $p(T\mathcal {N})$ , so in fact, $p(T \mathcal {M})\cong p(T\mathcal {N})$ .

Lemma 2.25. Let $\Delta \subset \mathcal {M}_1\times \mathcal {M}_2$ be a quasidiagonal, where $\mathcal {M}_i$ is a stratum or hyperelliptic locus, $M = (M_1,M_2)\in \Delta $ is generic, $\mathcal {C}$ a $\Delta $ -equivalence class of cylinders on M, and $\gamma $ a cross curve of a cylinder $C\in \mathcal {C}$ on $M_1$ . If $\operatorname {\mathrm {Col}} _{C, \gamma } \mathcal {M}_1$ is lower rank than $\mathcal {M}_1$ , then there must be a $\gamma ' \subset M_2$ generically parallel to $\gamma $ that is a cross curve of a cylinder in $\mathcal {C}$ .

Proof. Assume by contradiction no saddle of $\mathcal {M}_2$ collapses in $\operatorname {\mathrm {Col}}_{\mathcal {C},\gamma }\Delta $ , so ${\mathcal {M}_2^{\prime } := p_2(\operatorname {\mathrm {Col}}_{\mathcal {C}, \gamma }\Delta )\subset \mathcal {M}_2}$ . However, $\mathcal {M}_2^{\prime }$ is dimension at most one less than $\mathcal {M}_2$ by Lemma 2.23 and has lower rank than $\mathcal {M}_2$ by Theorem 2.1. This contradicts Lemma 2.24. Thus, some $\gamma ' \subset M_2$ collapses in $\operatorname {\mathrm {Col}} _{\mathcal {C},\gamma }\Delta $ . A priori, $\gamma '$ may cross multiple adjacent cylinders. Since we assumed M is generic, by Lemma 2.22, all cylinders must be simple. Adjacent simple cylinders meet at marked points, but we assumed that there are no marked points, so there are no adjacent cylinders.

Lemma 2.26. Let $\Delta \subset \mathcal {M}_1\times \mathcal {M}_2$ be a quasidiagonal, where $\mathcal {M}_i$ is a stratum or hyperelliptic locus, $M = (M_1,M_2)\in \Delta $ is generic, $\mathcal {C}$ a $\Delta $ -equivalence class of cylinders on M, and $\gamma $ a cross curve of a cylinder $C\in \mathcal {C}$ . Let $\mathcal {M}_i^{\prime } := \overline {p_i(\operatorname {\mathrm {Col}}_{\mathcal {C}, \gamma } \Delta )}$ . Then, $\operatorname {\mathrm {Col}}_{\mathcal {C},\gamma }\Delta \subset \mathcal {M}_1^{\prime } \times \mathcal {M}_2^{\prime }$ is a quasidiagonal, and $\mathcal {M}_i^{\prime }$ is a stratum or hyperelliptic locus.

Proof. Let $\Delta ' := \operatorname {\mathrm {Col}}_{\mathcal {C},\gamma }\Delta $ . By [AW23a, Lemma 9.1], $\Delta '$ is a prime invariant subvariety, so it is a quasidiagonal in $\mathcal {M}_1^{\prime }\times \mathcal {M}_2^{\prime }$ . It remains to show that $\mathcal {M}_i^{\prime }$ is a stratum or hyperelliptic locus. Let $M= (M_1,M_2)$ and $\mathcal {C}_i$ be the cylinders of $\mathcal {C}$ on $M_i$ . Let $M'=(M_1^{\prime },M_2^{\prime }) = \operatorname {\mathrm {Col}}_{\mathcal {C},\gamma }M$ . Without loss of generality, let $\gamma \subset M_1$ . Then, $\overline {p_1(\Delta ') }= \operatorname {\mathrm {Col}}_{\mathcal {C}_1,\gamma } \mathcal {M}_1$ , which is codimension $1$ by Lemma 2.23. In period coordinates, $T_{M}\Delta \subset H^1(M_1,\Sigma _1)\times H^1(M_2,\Sigma _2)$ , and the projection on each side gives $p_i(T_M\Delta ) = T_{M_i}\mathcal {M}_i$ . By Proposition 2.18, $T_{M'} \Delta '$ can be viewed as a subspace of $T_{M}\Delta $ , so $T_{M_2^{\prime }}\mathcal {M}_2^{\prime }$ is codimension at most $1$ in $T_{M_2}\mathcal {M}_2$ . Thus, $\mathcal {M}_2^{\prime }$ is codimension at most $1$ . If $\mathcal {M}_2^{\prime } \subset \mathcal {M}_2$ , $\mathcal {M}_2^{\prime }$ is full rank by Lemma 2.24. Otherwise, some saddle connection $\gamma ' \subset M_2$ collapses, so $\operatorname {\mathrm {Col}}_{\mathcal {C},\gamma }\Delta = \operatorname {\mathrm {Col}}_{\mathcal {C},\gamma '}\Delta $ and $\mathcal {M}_2 = \operatorname {\mathrm {Col}}_{\mathcal {C},\gamma '}\mathcal {M}_2$ , which is full rank by Lemma 2.24.

Definition 2.27. Let $\mathcal {M}$ be an invariant subvariety (in a potentially multi-component stratum). Let $M\in \mathcal {M}$ and $\mathcal {C}_1,\mathcal {C}_2$ be two disjoint $\mathcal {M}$ -parallel classes of cylinders. Let $\gamma _i$ be a cross curve on a cylinder in $\mathcal {C}_i$ Then, $(\mathcal {M}, M, \mathcal {C}_1, \mathcal {C}_2, \gamma _1, \gamma _2)$ is called a diamond. A diamond is called generic if M is generic and the components of $\mathcal {F} \operatorname {\mathrm {Col}}_{\mathcal {C}_1,\gamma _1,\mathcal {C}_2,\gamma _2}M$ have no automorphisms other than the identity.

We show the existence of many diamonds in multi-component invariant subvarieties similar to [AW23b, Lemma 3.31].

Lemma 2.28. Let $\mathcal {M}$ be a prime invariant subvariety of rank k. Then, a dense open set of surfaces in $\mathcal {M}$ has at least k disjoint equivalence classes of cylinders.

Proof. By Theorem 2.1, $\mathcal {M}_i = \overline {p_i(\mathcal {M})}$ has rank k. By [Wri15, Theorem 1.10], a dense set of horizontally periodic surfaces of $\mathcal {M}_i$ has at least k disjoint cylinder equivalence classes, so a dense set of surfaces $M \in p_i(\mathcal {M})$ has at least k disjoint cylinder equivalence classes. Since $p_i$ is a submersion, there is a dense set of surfaces $p_i^{-1}(M) \subset \mathcal {M}$ that have k disjoint cylinder equivalence classes. There is an open subset around each of these points, where these cylinders persist and remain disjoint.

Lemma 2.29. Let $\Delta \subset \mathcal {M}_1\times \mathcal {M}_2$ be an (equal area) quasidiagonal. We have the following similar statements.

1. (1) If, for any generic diamond $(\Delta ,M,\mathcal {C}_1, \mathcal {C}_2, \gamma _1, \gamma _2)$ , both $\operatorname {\mathrm {Col}}_{C_i,\gamma _i}\Delta $ , $i=1,2$ , are diagonals (respectively antidiagonals) up to rescaling (see Remark 2.5) and $\operatorname {\mathrm {Col}}_{C_1,\gamma _1,C_2,\gamma _2}\Delta $ is not $\mathcal {H}(0)$ , then $\Delta $ is a diagonal (respectively antidiagonal).

2. (2) If, for any generic diamond $(\Delta ,M,\mathcal {C}_1, \mathcal {C}_2, \gamma _1, \gamma _2)$ , both $\mathcal {F}\operatorname {\mathrm {Col}}_{C_i,\gamma _i}\Delta $ , $i=1,2$ , are diagonals (respectively antidiagonals) up to rescaling (see Remark 2.5) and $\mathcal {F}\operatorname {\mathrm {Col}}_{C_1,\gamma _1,C_2,\gamma _2}\Delta $ has genus $g\ge 2$ , then $\Delta $ is a diagonal (respectively antidiagonal).

Proof. Let $(\Delta , M,\mathcal {C}_1,\mathcal {C}_2,\gamma _1,\gamma _2)$ be any generic diamond. Assume both $\mathcal {F}\operatorname {\mathrm {Col}}_{C_i,\gamma _i}\Delta $ , $i=1,2$ are diagonals up to rescaling. Then, there are constants $r_i>0$ and isomorphisms $f_i:\mathcal {F}\operatorname {\mathrm {Col}}_{\mathcal {C}_i,\gamma _i} M_1 \to r_i\mathcal {F}\operatorname {\mathrm {Col}} _{\mathcal {C}_i,\gamma _i}M_2$ that restrict to isomorphisms

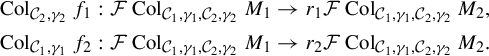$$ \begin{align*} &\operatorname{\mathrm{Col}}_{\mathcal{C}_2,\gamma_2}f_1: \mathcal{F}\operatorname{\mathrm{Col}}_{\mathcal{C}_1,\gamma_1,\mathcal{C}_2,\gamma_2}M_1 \to r_1\mathcal{F} \operatorname{\mathrm{Col}}_{\mathcal{C}_1,\gamma_1,\mathcal{C}_2,\gamma_2}M_2,\\ &\operatorname{\mathrm{Col}}_{\mathcal{C}_1,\gamma_1}f_2: \mathcal{F}\operatorname{\mathrm{Col}}_{\mathcal{C}_1,\gamma_1,\mathcal{C}_2,\gamma_2}M_1 \to r_2\mathcal{F} \operatorname{\mathrm{Col}}_{\mathcal{C}_1,\gamma_1,\mathcal{C}_2,\gamma_2}M_2. \end{align*} $$

We get that $r_1=r_2$ because isomorphic translation surfaces must have the same area. There is a unique translation surface isomorphism since we have chosen a generic diamond and the genus is greater than $1$ . Thus, $f_1,f_2$ agree on their overlap, so they extend to an isomorphism $f:M_1\to r_1M_2$ . We note that $r_1=1$ because we assumed $M_1,M_2$ have the same area. By Lemmas 2.21 and 2.28, a dense set of M belong to generic diamonds, so $\Delta $ is a diagonal. The other cases are similar.

3. Genus 2

As a base case for the induction, we must prove Theorem 1.8 for quasidiagonals in $\mathcal {H}(2)\times \mathcal {H}(2)$ .

Theorem 3.1. The only (equal area) quasidiagonal $\Delta \in \mathcal {H}(2)\times \mathcal {H}(2)$ is the diagonal $\{(M,M):M\in \mathcal {H}(2)\}$ .

Let $\Delta \subset \mathcal {H}(2)\times \mathcal {H}(2)$ be a quasidiagonal. Let $(M, M')\in \Delta $ be any generic surface. To prove the theorem, it suffices to show that $M'$ is equal to M, which is Lemma 3.4 below.

Lemma 3.2. Let $\mathcal {H}_1,\mathcal {H}_2$ be hyperelliptic components and $\Delta \subset \mathcal {H}_1,\times \mathcal {H}_2$ a quasidiagonal. Let $\mathcal {C}$ be a cylinder equivalence class on a surface $M\in \Delta $ . Then, $\mathcal {C}$ consists of one cylinder on each component.

Proof. By Lemma 2.15, $\mathcal {C}$ consists of one $\mathcal {H}_1$ -parallel class and one $\mathcal {H}_2$ -parallel class. For any stratum $\mathcal {H}$ , a $\mathcal {H}$ parallel class consists of an equivalence class of homologous cylinders, and on a hyperelliptic component, no two cylinders can be homologous.

Choose two disjoint cylinders $C_1,D$ on M. By Lemma 3.2, there are cylinders $C_1^{\prime },D'$ on $M'$ such that $\mathcal {C}_1= \{C_1,C_1^{\prime }\}$ and $\mathcal {D} = \{D,D'\}$ are $\Delta $ -parallel classes of cylinders. By Corollary 2.14, $C_1^{\prime },D'$ must be disjoint. We rotate $(M,M')$ to make $\mathcal {C}$ horizontal and perform a cylinder shear on $\mathcal {D}$ until M is horizontally periodic. By Lemma 2.9, $M'$ is also horizontally periodic. Let $C_2$ be the other horizontal cylinder on M. We fix a cross curve $\gamma _i$ of $C_i$ , where $\gamma _2$ is a boundary curve of D. Let $a_i$ be the period of $\gamma _i$ . Let $c_i$ be the period of the core curve of $C_i$ . See Figure 1. Because M is horizontally periodic, we have that $\operatorname {\mathrm {Im}} c_i=0$ . Label the corresponding cylinders, saddle connections, and periods of $M'$ with primes.

Figure 1 Horizontally periodic surface is $\mathcal {H}(2)$ .

Since $\Delta $ is cut out by linear equations in period coordinates, we have that

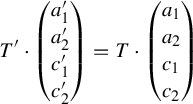$$ \begin{align*} T'\cdot \begin{pmatrix} a_1^{\prime}\\ a_2^{\prime}\\ c_1^{\prime}\\ c_2^{\prime} \end{pmatrix} = T\cdot \begin{pmatrix} a_1 \\ a_2 \\ c_1 \\ c_2 \end{pmatrix} \end{align*} $$

for some real matrices $T,T'$ for all periods in this periodic coordinate chart. By Theorem 2.1, the absolute periods determine each other, so the above matrices are invertible. Thus, we can assume $T'=\operatorname {\mathrm {Id}}$ . By Lemma 2.25, we may choose $a_1,a_1^{\prime }$ so that they are $\Delta $ -parallel, and $a_2,a_2^{\prime }$ are $\Delta $ -parallel since they are boundary curves of $\Delta $ -parallel cylinders. This means that $a_i^{\prime }$ does not depend on any period except $a_i$ . Changing $\operatorname {\mathrm {Im}} a_1,\operatorname {\mathrm {Im}} a_2$ does not affect $\operatorname {\mathrm {Im}} c_1^{\prime },\operatorname {\mathrm {Im}} c_2^{\prime }$ since the surface must remain horizontally periodic by Lemma 2.9. Thus, we can simplify the matrix

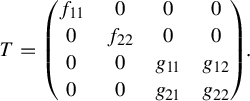$$ \begin{align*} T =\begin{pmatrix} f_{11} & 0 & 0 & 0\\ 0 & f_{22} & 0 & 0\\ 0 & 0 & g_{11} & g_{12}\\ 0 & 0 & g_{21} & g_{22} \end{pmatrix}\!. \end{align*} $$

Lemma 3.3. With the above notation, $g_{12}=g_{21}=0$ .

Proof. We can dilate $\mathcal {D}$ while keeping the surface horizontally periodic. This changes the circumferences $c_2$ without changing $c_1$ , so $g_{12} = 0$ . The following combination of shears will change $c_1$ without changing $c_2^{\prime }$ or $a_1^{\prime }$ . Dilate $\mathcal {D}$ while keeping the surface horizontally periodic. Now shrink the whole surface in the real direction (that is, by a matrix of the form $(\!\begin {smallmatrix} t & 0 \\ 0 & 1 \end {smallmatrix}\!)$ ) so that $c_2$ is its original size. This changes $c_1$ without changing $c_2$ , so $g_{21} = 0$ .

Lemma 3.4. Let $\Delta \subset \mathcal {H}(2)\times \mathcal {H}(2)$ be a quasidiagonal and $(M,M')\in \Delta $ be a generic surface. Then, $M,M'$ are isomorphic translation surfaces.

Proof. We label the surfaces using the notation above. Because the combinatorics of the surfaces are the same, it suffices to show that $T = \operatorname {\mathrm {Id}}$ . We first show $g_{22}=f_{22}$ ; $f_{11}=g_{11}$ is similar. Let $\mathcal {C}_2:=\{C_2,C_2^{\prime }\}$ . Start with $\mathcal {C}_2$ sheared so that $\gamma _2,\gamma _2^{\prime }$ are purely imaginary. We perform a cylinder shear on $\mathcal {C}_2$ until the first time $C_2$ or $C_2^{\prime }$ has a vertical saddle that is not fixed by the hyperelliptic involution. In fact, both of them must have a vertical saddle, and both saddles must not be fixed by the hyperelliptic involution since they are on the boundary of $\mathcal {D}$ . Thus, both cylinders must have been sheared by one full rotation, so the moduli must be equal. Let $h_2,h_2^{\prime }$ be the height of $C_2,C_2^{\prime }$ , respectively. Then, ${c_2}/{h_2} = {c_2^{\prime }}/{h_2^{\prime }} = {g_{22}c_2}/{f_{22}h_2}$ , so $f_{22}=g_{22}$ .

Now, we show $g_{11} = f_{22}$ . We shear $\mathcal {C}_1,\mathcal {C}_2$ so that $\gamma _1,\gamma _2$ are vertical, so that $M,M'$ are both vertically and horizontally periodic. By the same argument as above, $D, D'$ , which are now vertical cylinders, must have the same modulus. Thus,

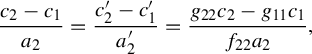$$ \begin{align*} \frac{c_2-c_1}{a_2} = \frac{c_2^{\prime}-c_1^{\prime}}{a_2^{\prime}} = \frac{g_{22}c_2-g_{11}c_1}{f_{22}a_2}, \end{align*} $$

so $f_{11}=f_{22}=g_{11}=g_{22}$ . Now, we see that

$$ \begin{align*} \begin{pmatrix} a_1^{\prime}\\ a_2^{\prime}\\ c_1^{\prime}\\ c_2^{\prime} \end{pmatrix} = f_{11} \begin{pmatrix} 1 &&&\\ &1&&\\ &&1&\\ &&&1 \end{pmatrix} \begin{pmatrix} a_1 \\ a_2 \\ c_1 \\ c_2 \end{pmatrix}\!. \end{align*} $$

Since we assumed both sides have the same area, we have that $f_{11}=1$ . Thus, $T = \operatorname {\mathrm {Id}}$ . This finishes the proof of Theorem 3.1.

4. Proof of main theorem

Definition 4.1. Let $\mathcal {H}$ be a stratum and $\mathcal {M} \subset \mathcal {H}$ an invariant subvariety. Here, $\mathcal {M}$ is full rank if $\operatorname {\mathrm {rk}} \mathcal {M} = \operatorname {\mathrm {rk}} \mathcal {H}$ .

Theorem 4.2. [MW18, Theorem 1.1]

An invariant variety is full rank if and only if it is a full stratum or a hyperelliptic locus.

Thus, Theorem 1.8 is equivalent to the following.

Theorem 4.3. Let $\mathcal {M}_1,\mathcal {M}_2$ be full rank invariant subvarieties in a stratum of translation surfaces in genus $g\ge 2$ . The only (equal area) quasidiagonals $\Delta \subset \mathcal {M}_1\times \mathcal {M}_2$ are the diagonal and antidiagonal when $\mathcal {M}_1= \mathcal {M}_2$ .

Proof. We use induction on rank and rel as follows. The base case is when $\operatorname {\mathrm {rk}} \Delta = 2$ and $\operatorname {\mathrm {rel}} \mathcal {M}_1,\operatorname {\mathrm {rel}} \mathcal {M}_2 = 0$ , that is, $\mathcal {M}_1$ and $\mathcal {M}_2$ are $\mathcal {H}(2)$ , which is proven in Theorem 3.1. As the induction hypothesis, assume the theorem holds for any $\Delta \subset \mathcal {M}_1\times \mathcal {M}_2$ , where $\mathcal {M}_1,\mathcal {M}_2$ are full rank, if $\operatorname {\mathrm {rk}} \Delta < r$ (and all values of $\operatorname {\mathrm {rel}} \mathcal {M}_1, \operatorname {\mathrm {rel}} \mathcal {M}_2$ ) or if $\operatorname {\mathrm {rk}} \Delta = r$ and $\operatorname {\mathrm {rel}} \mathcal {M}_1 +\operatorname {\mathrm {rel}} \mathcal {M}_2<s$ . We will prove the theorem assuming $\operatorname {\mathrm {rk}} \Delta = r$ and $\operatorname {\mathrm {rel}} \mathcal {M}_1+\operatorname {\mathrm {rel}} \mathcal {M}_2=s$ . We choose a generic diamond $(\Delta , (M_1,M_2),\mathcal {C}_1,\mathcal {C}_2,\gamma _1,\gamma _2)$ .

We first consider the rank $2$ case. Let $\Delta \subset \mathcal {M}_1\times \mathcal {M}_2$ , where $\mathcal {M}_i$ are $\mathcal {H}(2)$ or $\mathcal {H}(1,1)$ . We already proved the theorem for $\Delta \subset \mathcal {H}(2)\times \mathcal {H}(2)$ . Without loss of generality, we assume $\mathcal {M}_1 = \mathcal {H}(1,1)$ . We may choose the generic diamond such that ${\mathcal {C}_1,\mathcal {C}_2,\gamma _1,\gamma _2\subset M_1}$ . By Lemma 2.26, $\operatorname {\mathrm {Col}}_{\mathcal {C}_i,\gamma _i}\Delta \subset \mathcal {H}(2) \times \mathcal {M}_2^{\prime }$ is a quasidiagonal, so it is rank $2$ . Here, $\mathcal {M}_2$ is $\mathcal {H}(2)$ or $\mathcal {H}(1,1)$ , and $\mathcal {M}_2^{\prime }$ is a rank $2$ and a collapse of $\mathcal {M}_2$ , so it does not have marked points. By the induction hypothesis, $\operatorname {\mathrm {Col}}_{\mathcal {C}_i,\gamma _i}\Delta $ is a diagonal. Since $\operatorname {\mathrm {Col}}_{\mathcal {C}_1,\gamma _1,\mathcal {C}_2,\gamma _2}\mathcal {M}_1 = \mathcal {H}(0,0)$ , we may use the first statement of Lemma 2.29 to conclude that $\Delta $ is a diagonal.

Now we assume the rank is at least $3$ . By Lemma 2.26, $\operatorname {\mathrm {Col}}_{\mathcal {C}_i,\gamma _i}\Delta \subset \mathcal {M}_1^{\prime }\times \mathcal {M}_2^{\prime }$ is a quasidiagonal, where $\mathcal {M}_j^{\prime }$ are full rank. Since marked points do not affect the rank, we may forget marked points. Let $\mathcal {F}$ be the functor that forgets marked points. By the induction hypothesis, $\mathcal {F}\operatorname {\mathrm {Col}}_{\mathcal {C}_i,\gamma _i}\Delta $ is a diagonal or antidiagonal for $i=1,2$ . If $\mathcal {M}_1$ and $\mathcal {M}_2$ are hyperelliptic loci, then so are $\mathcal {F}\operatorname {\mathrm {Col}}_{\mathcal {C}_j,\gamma _j}\mathcal {M}_i$ , so $\mathcal {F} \operatorname {\mathrm {Col}} _{\mathcal {C}_j,\gamma _j}\Delta $ must be a diagonal (recall that for a hyperelliptic locus, diagonals and antidiagonals are the same). Then by Lemma 2.29, $\Delta $ must be a diagonal. Now it remains to consider when $\mathcal {M}_1$ or $\mathcal {M}_2$ is not hyperelliptic. In this case, the rank is at least $3$ , so by Lemma 2.28, we can find three disjoint equivalence classes of cylinders $\mathcal {C}_1,\mathcal {C}_2,\mathcal {C}_3$ such that each of $\mathcal {F}\operatorname {\mathrm {Col}} _{\mathcal {C}_i,\gamma _i}\Delta $ is a diagonal or quasidiagonal. By the pigeon hole principle, there are two $(\mathcal {C}_i,\gamma _i)$ such that $\mathcal {F}\operatorname {\mathrm {Col}} _{\mathcal {C}_i,\gamma _i}\Delta $ are either both diagonals or both quasidiagonals. Now, the second statement of Lemma 2.29 finishes the proof.