Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Конев, Р А
Konev, R A
Рыжиков, Валерий Валентинович
and
Ryzhikov, Valerii Valentinovich
2014.
О наборе спектральных кратностей $\{2,4,…,2^n\}$ для вполне эргодических $\mathbb{Z}^2$-действий.
Математические заметки,
Vol. 96,
Issue. 3,
p.
383.
Konev, R. A.
and
Ryzhikov, V. V.
2014.
On the collection of spectral multiplicities {2, 4, …, 2 n } for totally ergodic ℤ2-actions.
Mathematical Notes,
Vol. 96,
Issue. 3-4,
p.
360.
Kunde, Philipp
2016.
Smooth diffeomorphisms with homogeneous spectrum and disjointness of convolutions.
Journal of Modern Dynamics,
Vol. 10,
Issue. 02,
p.
439.
Ryzhikov, V. V.
and
Troitskaya, A. E.
2020.
Mixing Flows with Homogeneous Spectrum of Multiplicity 2.
Journal of Mathematical Sciences,
Vol. 248,
Issue. 5,
p.
642.
Kanigowski, Adam
and
Lemańczyk, Mariusz
2020.
Encyclopedia of Complexity and Systems Science.
p.
1.
Stepin, Anatoly
and
Tikhonov, Sergey
2021.
Topology, Geometry, and Dynamics.
Vol. 772,
Issue. ,
p.
311.
Danilenko, Alexandre I.
and
Silva, Cesar E.
2022.
Encyclopedia of Complexity and Systems Science.
p.
1.
Danilenko, Alexandre I.
Kosloff, Zemer
and
Roy, Emmanuel
2022.
Nonsingular Poisson Suspensions.
Journal d'Analyse Mathématique,
Vol. 146,
Issue. 2,
p.
741.
Kanigowski, Adam
and
Lemańczyk, Mariusz
2023.
Ergodic Theory.
p.
109.
Danilenko, Alexandre I.
and
Silva, Cesar E.
2023.
Ergodic Theory.
p.
233.
Ryzhikov, V. V.
2023.
Spectra of Self-Similar Ergodic Actions.
Mathematical Notes,
Vol. 113,
Issue. 1-2,
p.
274.
Ryzhikov, Valerii Valentinovich
2023.
Спектры самоподобных эргодических действий.
Математические заметки,
Vol. 113,
Issue. 2,
p.
273.
BURGUET, DAVID
and
SHI, RUXI
2024.
Multiplicity of topological systems.
Ergodic Theory and Dynamical Systems,
Vol. 44,
Issue. 10,
p.
2832.

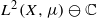 by
by 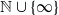 are realizable as ℳ(
are realizable as ℳ(