Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Glasner, Eli
1990.
A topological version of a theorem of Veech and almost simple flows.
Ergodic Theory and Dynamical Systems,
Vol. 10,
Issue. 3,
p.
463.
Flaminio, L.
1993.
Mixing 𝑘-fold independent processes of zero entropy.
Proceedings of the American Mathematical Society,
Vol. 118,
Issue. 4,
p.
1263.
Yancey, Kelly B.
2013.
Topologically weakly mixing homeomorphisms of the Klein bottle that are uniformly rigid.
Topology and its Applications,
Vol. 160,
Issue. 14,
p.
1853.
Yancey, Kelly B.
2013.
On weakly mixing homeomorphisms of the two-torus that are uniformly rigid.
Journal of Mathematical Analysis and Applications,
Vol. 399,
Issue. 2,
p.
524.
Glasner, E.
Thouvenot, J.-P.
and
Weiss, B.
2022.
On some generic classes of ergodic measure preserving transformations.
Transactions of the Moscow Mathematical Society,
Vol. 82,
Issue. 0,
p.
15.

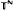 , using a category argument, we produce a large family of homeomorphisms such that for every element
, using a category argument, we produce a large family of homeomorphisms such that for every element 
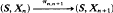 are isometric. We also show that, for every
are isometric. We also show that, for every 