Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Flatto, Leopold
and
Lagarias, Jeffrey C.
1996.
The lap-counting function for linear mod one transformations I: explicit formulas and renormalizability.
Ergodic Theory and Dynamical Systems,
Vol. 16,
Issue. 3,
p.
451.
Boyd, David
1996.
On beta expansions for Pisot numbers.
Mathematics of Computation,
Vol. 65,
Issue. 214,
p.
841.
Boyd, David
1996.
On the beta expansion for Salem numbers of degree 6.
Mathematics of Computation,
Vol. 65,
Issue. 214,
p.
861.
Point, F.
and
Bruyère, V.
1997.
On the cobham-semenov theorem.
Theory of Computing Systems,
Vol. 30,
Issue. 2,
p.
197.
Brown, G.
and
Yin, Qinghe
1999.
β-Expansions and Frequency of Zero.
Acta Mathematica Hungarica,
Vol. 84,
Issue. 4,
p.
275.
Flatto, Leopold
and
Lagarias, Jeffrey C
2000.
The lap-counting and zeta functions of the tent map.
Nonlinearity,
Vol. 13,
Issue. 4,
p.
1055.
Lagarias, Jeffrey C.
2001.
On the Normality of Arithmetical Constants.
Experimental Mathematics,
Vol. 10,
Issue. 3,
p.
355.
Groeneveld, J.
and
Klages, R.
2002.
Negative and Nonlinear Response in an Exactly Solved Dynamical Model of Particle Transport.
Journal of Statistical Physics,
Vol. 109,
Issue. 3-4,
p.
821.
Bassino, Frédérique
2002.
LATIN 2002: Theoretical Informatics.
Vol. 2286,
Issue. ,
p.
141.
Niederreiter, Harald
and
Shparlinski, Igor E.
2003.
Applied Algebra, Algebraic Algorithms and Error-Correcting Codes.
Vol. 2643,
Issue. ,
p.
6.
Fan, Ying Wai
and
Berenhaut, K.S.
2005.
A bound for linear recurrence relations with unbounded order.
Computers & Mathematics with Applications,
Vol. 50,
Issue. 3-4,
p.
509.
Berenhaut, Kenneth S.
and
Foley, John D.
2006.
Explicit bounds for multidimensional linear recurrences with restricted coefficients.
Journal of Mathematical Analysis and Applications,
Vol. 322,
Issue. 2,
p.
1159.
Barat, Guy
Berthé, Valérie
Liardet, Pierre
and
Thuswaldner, Jörg
2006.
Dynamical directions in numeration.
Annales de l'Institut Fourier,
Vol. 56,
Issue. 7,
p.
1987.
Berenhaut, Kenneth S.
and
Morton, Daniel C.
2006.
Second-order bounds for linear recurrences with negative coefficients.
Journal of Computational and Applied Mathematics,
Vol. 186,
Issue. 2,
p.
504.
Verger-Gaugry, Jean-Louis
2006.
On gaps in Rényi β-expansions of unity for β>1 an algebraic number.
Annales de l'Institut Fourier,
Vol. 56,
Issue. 7,
p.
2565.
HBAIB, M.
and
MKAOUAR, M.
2006.
SUR LE BÊTA-DÉVELOPPEMENT DE 1 DANS LE CORPS DES SÉRIES FORMELLES.
International Journal of Number Theory,
Vol. 02,
Issue. 03,
p.
365.
Berenhaut, Kenneth S.
Allen, Edward E.
and
Fraser, Sam J.
2006.
Bounds on coefficients of reciprocals of formal power series with rapidly decreasing coefficients.
Discrete Dynamics in Nature and Society,
Vol. 2006,
Issue. 1,
Jorgensen, Palle E. T.
Kornelson, Keri
and
Shuman, Karen
2007.
Harmonic analysis of iterated function systems with overlap.
Journal of Mathematical Physics,
Vol. 48,
Issue. 8,
Verger-Gaugry, Jean-Louis
2008.
On the dichotomy of Perron numbers and beta-conjugates.
Monatshefte für Mathematik,
Vol. 155,
Issue. 3-4,
p.
277.
Mukunda, Keshav
2010.
Pisot Numbers from {0, 1}-Polynomials.
Canadian Mathematical Bulletin,
Vol. 53,
Issue. 1,
p.
140.
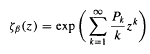
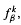 , and the lap-counting function
, and the lap-counting function 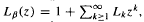 where Lk counts the number of monotonic pieces of the kth iterate
where Lk counts the number of monotonic pieces of the kth iterate 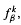 . For β-transformations these functions are related by ζβ(z) = (1 − z)Lβ(z). The function ζβ(z) is meromorphic in the unit disk, is holomorphic in {z: |z| < 1/β}, has a simple pole at z = 1/β, and has no other singularities with |z| = 1/β. Let M(β) denote the minimum modulus of any pole of ζβ(z) in |z| < 1 other than z = 1/β, and set M(β) = 1 if no other pole exists with |z| < 1. Then Pk = βk + O((M(β)−1+ε)k) for any ε > 0. This paper shows that M(β) is a continuous function, that (
. For β-transformations these functions are related by ζβ(z) = (1 − z)Lβ(z). The function ζβ(z) is meromorphic in the unit disk, is holomorphic in {z: |z| < 1/β}, has a simple pole at z = 1/β, and has no other singularities with |z| = 1/β. Let M(β) denote the minimum modulus of any pole of ζβ(z) in |z| < 1 other than z = 1/β, and set M(β) = 1 if no other pole exists with |z| < 1. Then Pk = βk + O((M(β)−1+ε)k) for any ε > 0. This paper shows that M(β) is a continuous function, that (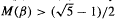 for all β, and that
for all β, and that 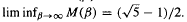 An asymptotic formula is derived for M(β) as β → 1+, which implies that M(β) < 1 for all β in an interval (1, 1 + c0). The set
An asymptotic formula is derived for M(β) as β → 1+, which implies that M(β) < 1 for all β in an interval (1, 1 + c0). The set 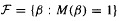 is shown to have properties analogous to the set of Pisot numbers. It is closed, totally disconnected, has smallest element ≥ 1 + C0 and contains infinitely many β falling in each interval [n, n + 1) for n ∈ ℤ+. All known members of
is shown to have properties analogous to the set of Pisot numbers. It is closed, totally disconnected, has smallest element ≥ 1 + C0 and contains infinitely many β falling in each interval [n, n + 1) for n ∈ ℤ+. All known members of 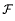 are algebraic integers which are either Pisot or Salem numbers.
are algebraic integers which are either Pisot or Salem numbers.
