Contents
Research Article
Holomorphic families of quasi-Fuchsian groups
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 207-212
-
- Article
- Export citation
Non-uniqueness of measures of maximal entropy for subshifts of finite type
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 213-235
-
- Article
- Export citation
The zeta function of the beta transformation
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 237-266
-
- Article
- Export citation
Analytic destruction of invariant circles
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 267-298
-
- Article
- Export citation
Anosov flows which are uniformly expanding at periodic points
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 299-304
-
- Article
- Export citation
Un théorème de préparation pour fonctions à développement Tchébychévien
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 305-329
-
- Article
- Export citation
Distortion results and invariant Cantor sets of unimodal maps
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 331-349
-
- Article
- Export citation
Basins of attraction near homoclinic tangencies
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 351-390
-
- Article
- Export citation
Rational functions with no recurrent critical points
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 391-414
-
- Article
- Export citation
Front matter
ETS volume 14 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
ETS volume 14 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation
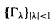 of infinitely generated quasi-Fuchsian groups such that the Hausdorff dimension of the limit set
of infinitely generated quasi-Fuchsian groups such that the Hausdorff dimension of the limit set 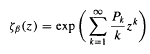
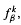 , and the lap-counting function
, and the lap-counting function 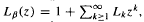 where
where 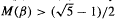 for all β, and that
for all β, and that 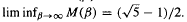 An asymptotic formula is derived for
An asymptotic formula is derived for 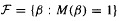 is shown to have properties analogous to the set of Pisot numbers. It is closed, totally disconnected, has smallest element ≥ 1 +
is shown to have properties analogous to the set of Pisot numbers. It is closed, totally disconnected, has smallest element ≥ 1 + 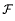 are algebraic integers which are either Pisot or Salem numbers.
are algebraic integers which are either Pisot or Salem numbers.