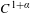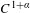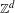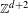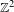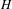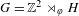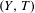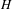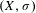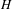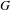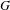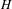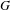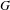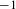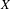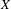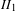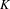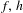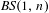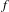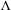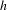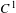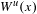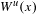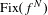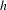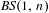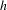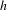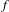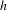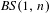Contents
Original Article
On the statistical stability of Lorenz attractors with a
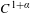 $C^{1+\unicode[STIX]{x1D6FC}}$ stable foliation
$C^{1+\unicode[STIX]{x1D6FC}}$ stable foliation
-
- Published online by Cambridge University Press:
- 16 April 2018, pp. 3169-3184
-
- Article
- Export citation
A generalization of the simulation theorem for semidirect products
-
- Published online by Cambridge University Press:
- 10 April 2018, pp. 3185-3206
-
- Article
- Export citation
Recurrence on affine Grassmannians
-
- Published online by Cambridge University Press:
- 05 April 2018, pp. 3207-3223
-
- Article
- Export citation
On the relation between Gibbs and
 $g$-measures
$g$-measures
-
- Published online by Cambridge University Press:
- 28 March 2018, pp. 3224-3249
-
- Article
- Export citation
Two special subgroups of the universal sofic group
-
- Published online by Cambridge University Press:
- 10 April 2018, pp. 3250-3261
-
- Article
- Export citation
Marked length rigidity for Fuchsian buildings
-
- Published online by Cambridge University Press:
- 13 March 2018, pp. 3262-3291
-
- Article
- Export citation
K-property for Maharam extensions of non-singular Bernoulli and Markov shifts
-
- Published online by Cambridge University Press:
- 05 April 2018, pp. 3292-3321
-
- Article
- Export citation
Weak colored local rules for planar tilings
-
- Published online by Cambridge University Press:
- 05 April 2018, pp. 3322-3346
-
- Article
- Export citation
A counterexample to the composition condition conjecture for polynomial Abel differential equations
-
- Published online by Cambridge University Press:
- 13 March 2018, pp. 3347-3352
-
- Article
- Export citation
Any Baumslag–Solitar action on surfaces with a pseudo-Anosov element has a finite orbit
-
- Published online by Cambridge University Press:
- 28 March 2018, pp. 3353-3364
-
- Article
- Export citation
Statistics of patterns in typical cut and project sets
-
- Published online by Cambridge University Press:
- 13 March 2018, pp. 3365-3387
-
- Article
- Export citation
On the arithmetic dynamics of monomial maps
-
- Published online by Cambridge University Press:
- 13 March 2018, pp. 3388-3406
-
- Article
- Export citation
Mixing for suspension flows over skew-translations and time-changes of quasi-abelian filiform nilflows
-
- Published online by Cambridge University Press:
- 28 March 2018, pp. 3407-3436
-
- Article
- Export citation
Böttcher coordinates at fixed indeterminacy points
-
- Published online by Cambridge University Press:
- 13 March 2018, pp. 3437-3456
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 39 Issue 12 Cover and Front matter
-
- Published online by Cambridge University Press:
- 04 November 2019, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
ETS volume 39 Issue 12 Cover and Back matter
-
- Published online by Cambridge University Press:
- 04 November 2019, pp. b1-b2
-
- Article
-
- You have access
- Export citation