Contents
Research Article
Augmented dimension groups and ordered cohomology
-
- Published online by Cambridge University Press:
- 01 February 2009, pp. 1-35
-
- Article
- Export citation
Aperiodic substitution systems and their Bratteli diagrams
-
- Published online by Cambridge University Press:
- 01 February 2009, pp. 37-72
-
- Article
- Export citation
On Khintchine exponents and Lyapunov exponents of continued fractions
-
- Published online by Cambridge University Press:
- 01 February 2009, pp. 73-109
-
- Article
- Export citation
Ergodic theorem for the algebra of operators in 𝕃p
-
- Published online by Cambridge University Press:
- 01 February 2009, pp. 111-116
-
- Article
- Export citation
On Anosov diffeomorphisms with asymptotically conformal periodic data
-
- Published online by Cambridge University Press:
- 01 February 2009, pp. 117-136
-
- Article
- Export citation
Bounded-type Siegel disks of a one-dimensional family of entire functions
-
- Published online by Cambridge University Press:
- 01 February 2009, pp. 137-164
-
- Article
- Export citation
Embeddings of dynamical systems into cellular automata
-
- Published online by Cambridge University Press:
- 01 February 2009, pp. 165-177
-
- Article
- Export citation
Robustly expansive codimension-one homoclinic classes are hyperbolic
-
- Published online by Cambridge University Press:
- 01 February 2009, pp. 179-200
-
- Article
- Export citation
Resonance between Cantor sets
-
- Published online by Cambridge University Press:
- 01 February 2009, pp. 201-221
-
- Article
- Export citation
An asymptotic-numerical approach for examining global solutions to an ordinary differential equation
-
- Published online by Cambridge University Press:
- 01 February 2009, pp. 223-253
-
- Article
- Export citation
Billiards in polygons and homogeneous foliations on C2
-
- Published online by Cambridge University Press:
- 01 February 2009, pp. 255-271
-
- Article
- Export citation
Abstract fluctuation theorem
-
- Published online by Cambridge University Press:
- 01 February 2009, pp. 273-279
-
- Article
- Export citation
Dimensions of compact invariant sets of some expanding maps
-
- Published online by Cambridge University Press:
- 01 February 2009, pp. 281-315
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 29 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 09 January 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
ETS volume 29 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 09 January 2009, pp. b1-b6
-
- Article
-
- You have access
- Export citation

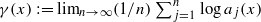 when the limit exists. The Khintchine spectrum dim
when the limit exists. The Khintchine spectrum dim  , is neither concave nor convex. This is a new phenomenon from the usual point of view of multifractal analysis. Fast Khintchine exponents defined by
, is neither concave nor convex. This is a new phenomenon from the usual point of view of multifractal analysis. Fast Khintchine exponents defined by 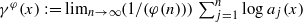 are also studied, where φ(
are also studied, where φ(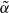 of the algebra of bounded linear operators in 𝕃
of the algebra of bounded linear operators in 𝕃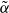 is proved.
is proved.