Contents
Research Article
Transitivity of codimension-one Anosov actions of ℝk on closed manifolds
-
- Published online by Cambridge University Press:
- 18 January 2010, pp. 1-22
-
- Article
- Export citation
Quasiregular dynamics on the n-sphere
-
- Published online by Cambridge University Press:
- 18 January 2010, pp. 23-31
-
- Article
- Export citation
Measures with uniform scaling scenery
-
- Published online by Cambridge University Press:
- 18 January 2010, pp. 33-48
-
- Article
- Export citation
A topological lens for a measure-preserving system
-
- Published online by Cambridge University Press:
- 02 February 2010, pp. 49-75
-
- Article
- Export citation
An invariant of finitary codes with finite expected square root coding length
-
- Published online by Cambridge University Press:
- 18 January 2010, pp. 77-90
-
- Article
- Export citation
Non-expansive directions for ℤ2 actions
-
- Published online by Cambridge University Press:
- 24 March 2010, pp. 91-112
-
- Article
- Export citation
Nil–Bohr sets of integers
-
- Published online by Cambridge University Press:
- 24 November 2009, pp. 113-142
-
- Article
-
- You have access
- Export citation
Multifractal analysis of weak Gibbs measures for non-uniformly expanding C1 maps
-
- Published online by Cambridge University Press:
- 18 January 2010, pp. 143-164
-
- Article
- Export citation
Entropy, horseshoes and homoclinic trajectories on trees, graphs and dendrites
-
- Published online by Cambridge University Press:
- 02 February 2010, pp. 165-175
-
- Article
- Export citation
Correction
Entropy, horseshoes and homoclinic trajectories on trees, graphs and dendrites – ERRATUM
-
- Published online by Cambridge University Press:
- 25 June 2010, p. 177
-
- Article
- Export citation
Research Article
Equilibrium states for partially hyperbolic horseshoes
-
- Published online by Cambridge University Press:
- 18 January 2010, pp. 179-195
-
- Article
- Export citation
Multipliers of periodic orbits in spaces of rational maps
-
- Published online by Cambridge University Press:
- 11 March 2010, pp. 197-243
-
- Article
- Export citation
Analytic integrability of quadratic–linear polynomial differential systems
-
- Published online by Cambridge University Press:
- 04 November 2009, pp. 245-258
-
- Article
- Export citation
Polymorphisms and adiabatic chaos
-
- Published online by Cambridge University Press:
- 02 February 2010, pp. 259-284
-
- Article
- Export citation
Rank-one ℤd actions and directional entropy
-
- Published online by Cambridge University Press:
- 11 December 2009, pp. 285-299
-
- Article
- Export citation
Non-singular Smale flows on three-dimensional manifolds and Whitehead torsion
-
- Published online by Cambridge University Press:
- 24 November 2009, pp. 301-315
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 31 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 07 January 2011, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
ETS volume 31 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 07 January 2011, pp. b1-b6
-
- Article
-
- You have access
- Export citation

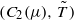 defined on the space of twofold couplings of
defined on the space of twofold couplings of 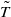 . Some of our main results are as follows: (i)
. Some of our main results are as follows: (i)