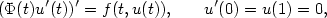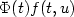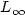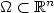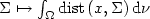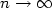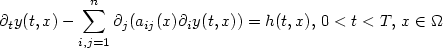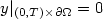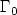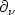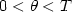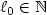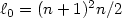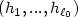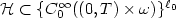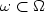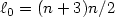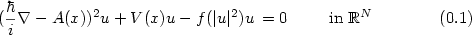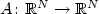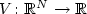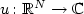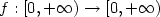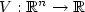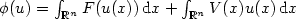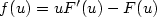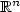Refine listing
Actions for selected content:
Contents
Research Article
Existence and L∞ estimates of some Mountain-Pass type solutions
-
- Published online by Cambridge University Press:
- 02 July 2009, pp. 499-508
-
- Article
- Export citation
Long-term planning versus short-term planning in the asymptotical location problem
-
- Published online by Cambridge University Press:
- 30 May 2008, pp. 509-524
-
- Article
- Export citation
Lipschitz stability in the determination of the principal part ofa parabolic equation
-
- Published online by Cambridge University Press:
- 19 July 2008, pp. 525-554
-
- Article
- Export citation
Spectrum of the Laplacian in a narrow curved strip with combined Dirichlet and Neumann boundary conditions
-
- Published online by Cambridge University Press:
- 30 May 2008, pp. 555-568
-
- Article
- Export citation
A geometric lower bound on Grad's number
-
- Published online by Cambridge University Press:
- 26 April 2008, pp. 569-575
-
- Article
- Export citation
Critical points of Ambrosio-Tortorelli convergeto critical points of Mumford-Shahin the one-dimensional Dirichlet case
-
- Published online by Cambridge University Press:
- 24 June 2008, pp. 576-598
-
- Article
- Export citation
Control Lyapunov functions and stabilization by meansof continuous time-varying feedback
-
- Published online by Cambridge University Press:
- 19 July 2008, pp. 599-625
-
- Article
- Export citation
Mesh-independence and preconditioning for solving parabolic control problems with mixed control-state constraints
-
- Published online by Cambridge University Press:
- 19 July 2008, pp. 626-652
-
- Article
- Export citation
Multi-peak solutions for magnetic NLS equations without non-degeneracy conditions
-
- Published online by Cambridge University Press:
- 20 August 2008, pp. 653-675
-
- Article
- Export citation
Magnetization switching on small ferromagneticellipsoidal samples
-
- Published online by Cambridge University Press:
- 19 July 2008, pp. 676-711
-
- Article
- Export citation
Nonlinear diffusion equations with variable coefficients as gradient flows in Wasserstein spaces
-
- Published online by Cambridge University Press:
- 19 July 2008, pp. 712-740
-
- Article
- Export citation
Correction
Corrigendum to: “On the circle criterionfor boundary control systems in factor form: Lyapunov stabilityand Lur'e equations”
-
- Published online by Cambridge University Press:
- 18 June 2009, pp. 741-744
-
- Article
- Export citation