Unique continuation property near a cornerand its fluid-structurecontrollability consequences

Abstract

We study a non standard unique continuation property for the biharmonic spectral problem $\Delta^2 w=-\lambda\Delta w$ 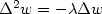in a 2D corner with homogeneous Dirichlet boundary conditions and a supplementary third order boundary condition on one side of the corner. We prove that if the corner has an angle $0<\theta_0<2\pi$ 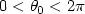, $\theta_0\not=\pi$ 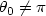and $\theta_0\not=3\pi/2$ 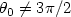, a unique continuation property holds. Approximate controllability of a 2-D linear fluid-structure problem follows from this property, with a control acting on the elastic side of a corner in a domain containing a Stokes fluid. The proof of the main result is based in a power series expansion of the eigenfunctions near the corner, the resolution of a coupled infinite set of finite dimensional linear systems, and a result of Kozlov, Kondratiev and Mazya, concerning the absence of strong zeros for the biharmonic operator [Math. USSR Izvestiya 34 (1990) 337–353]. We also show how the same methodologyused here can be adapted to exclude domains with corners to have a localversion of the Schiffer property for the Laplace operator.