Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T21:12:19.210Z Has data issue: false hasContentIssue false
  • English
  • Français

Computation of bifurcated branches in a free boundary problem arising in combustion theory

Published online by Cambridge University Press:  15 April 2002

Olivier Baconneau ,
Claude-Michel Brauner  and
Alessandra Lunardi
Olivier Baconneau
Affiliation:
Mathématiques Appliquées de Bordeaux, Université Bordeaux I, 33405 Talence Cedex, France. e-mail: Olivier.Baconneau@math.u-bordeaux.fr; Claude-Michel.Brauner@math.u-bordeaux.fr
Claude-Michel Brauner
Affiliation:
Mathématiques Appliquées de Bordeaux, Université Bordeaux I, 33405 Talence Cedex, France. e-mail: Olivier.Baconneau@math.u-bordeaux.fr; Claude-Michel.Brauner@math.u-bordeaux.fr
Alessandra Lunardi
Affiliation:
Dipartimento di Matematica, Università di Parma Via D'Azeglio 85/A, 43100 Parma, Italy. e-mail: lunardi@prmat.math.unipr.it
Get access

Abstract

We consider a parabolic 2D Free Boundary Problem, with jump conditions at the interface. Its planar travelling-wave solutions are orbitally stableprovided the bifurcation parameter $u_*$ 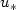does not exceed a critical value $u_{*}^{c}$ 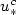. The latter isthe limit of a decreasing sequence $(u_{*}^{k})$ 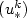of bifurcation points. The paper deals with the study of the 2D bifurcated branchesfrom the planar branch, for small k. Our technique is based on the elimination of the unknown front, turning the problem into a fully nonlinear one, to which we canapply the Crandall-Rabinowitz bifurcation theorem for a local study.We point out that the fully nonlinear reformulation of the FBP can also serve to developefficient numerical schemes in view of global information, such as techniques based on arc length continuation.

Keywords

Free Boundary Problembifurcationfully nonlinear equationscontinuation.
Type
Research Article
Information
ESAIM: Mathematical Modelling and Numerical Analysis , Volume 34 , Issue 2: Special issue for R. Teman's 60th birthday , March 2000 , pp. 223 - 339
Copyright
© EDP Sciences, SMAI, 2000

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

O. Baconneau, Bifurcation de fronts pour un problème à frontière libre en combustion. Ph.D. thesis, Université Bordeaux 1 (1998).
C.-M. Brauner, J. Hulshof and A. Lunardi, A general approach to stability in free boundary problems. J. Differential Equations (to appear).
C.-M. Brauner and A. Lunardi, Bifurcation of nonplanar travelling waves in a free boundary problem. Nonlinear Analysis T. M. A. (to appear).
Brauner, C.-M., Lunardi, A. and Schmidt-Lainé, Cl., Stability of travelling waves with interface conditions. Nonlinear Analysis T. M. A. 19 (1992) 465-484. CrossRef
Brauner, C.-M., Lunardi, A. and Schmidt-Lainé, Cl., Multidimensional stability analysis of planar travelling waves. Appl. Math. Lett. 7 (1994) 1-4. CrossRef
C.-M. Brauner, A. Lunardi and Cl. Schmidt-Lainé, Stability of travelling waves in a multidimensional free boundary problem. Nonlinear Analysis T.M.A. (to appear).
Crandall, M.G. and Rabinowitz, P.H., Bifurcation from simple eigenvalues. J. Funct. Anal. 8 (1971) 321-340. CrossRef
H.B. Keller, Numerical solution of bifurcation and non linear eigenvalue problems, P. Rabinowitz Ed., Academic Press, New York (1978) 73-94.
Sattinger, D.H., Stability of waves of nonlinear parabolic equations. Adv. Math. 22 (1976) 141-178. CrossRef
Stewart, D.S. and Ludford, G.S.S., The acceleration of fast deflagration waves. Z.A.M.M. 63 (1983) 291-302.
J.L. Vazquez, The Free Boundary Problem for the Heat Equation with fixed Gradient Condition, Proc. Int. Conf. "Free Boundary Problem and Applications'', Zakopane, Pitman Res. Notes Math. 363, Longman (1996).