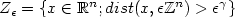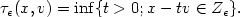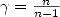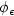Refine listing
Actions for selected content:
Contents
Research Article
Un schéma d'interpolation rationnel sur un quadrilatèrede classeC 2
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 913-922
-
- Article
- Export citation
Splitting d'opérateur pour l'équation de transportneutronique en géométrie bidimensionnelle plane
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 1109-1122
-
- Article
- Export citation
A model problem for boundary layers of thin elastic shells
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 1-30
-
- Article
- Export citation
Analysis of the hydrostatic approximation in oceanography with compression term
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 525-537
-
- Article
- Export citation
Introduction
Préface
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. I-II
-
- Article
- Export citation
Research Article
Asymptotic formulas for perturbations in the electromagnetic fields due to the presence of inhomogeneities of small diameter
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 723-748
-
- Article
- Export citation
Convergence rate of a finite volume scheme for the linear convection-diffusion equation on locally refined meshes
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 1123-1149
-
- Article
- Export citation
Fast Singular Oscillating Limits and Global Regularity for the 3D Primitive Equations of Geophysics
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 201-222
-
- Article
- Export citation
Some models of Cahn-Hilliard equationsin nonisotropic media
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 539-554
-
- Article
- Export citation
On the convergence of SCF algorithmsfor the Hartree-Fock equations
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 749-774
-
- Article
- Export citation
Bipolar Barotropic Non-Newtonian Compressible Fluids
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 923-934
-
- Article
- Export citation
A moving mesh fictitious domain approach for shape optimizationproblems
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 31-45
-
- Article
- Export citation
Local Solutions for Stochastic Navier Stokes Equations
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 241-273
-
- Article
- Export citation
existence of solutions for an elliptic-algebraic systemdescribing heat explosion in a two-phase medium
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 555-573
-
- Article
- Export citation
On the distribution of free path lengths for the periodic Lorentz gas II
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 1151-1163
-
- Article
- Export citation
A domain splitting method for heat conduction problemsin composite materials
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 47-62
-
- Article
- Export citation
On the domain geometry dependence of the LBB condition
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 935-951
-
- Article
- Export citation
Error Control and Andaptivity for a Phase Relaxation Model
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 775-797
-
- Article
- Export citation
StructuralProperties of Solutions to Total Variation Regularization Problems
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 799-810
-
- Article
- Export citation
Around 3D Boltzmann non linear operator without angular cutoff, a new formulation
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 575-590
-
- Article
- Export citation