Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-28T20:20:35.248Z Has data issue: false hasContentIssue false
  • English
  • Français

Finite Volume Box Schemes and Mixed Methods

Published online by Cambridge University Press:  15 April 2002

Jean-Pierre Croisille
Jean-Pierre Croisille*
Affiliation:
Département de Mathématiques, Université de Metz, 57045 Metz, France. (croisil@poncelet.univ-metz.fr)
Get access

Abstract

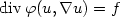We present the numerical analysis on the Poisson problem of two mixed Petrov-Galerkin finite volume schemes for equations in divergence form $\mathop{\rm div}\nolimits\varphi(u,\nabla u)=f$ . The first scheme, which has been introduced in [CITE], is a generalization in two dimensions of Keller's box-scheme. The second scheme is the dual of the first one, and is a cell-centeredscheme for u and the flux φ. For the first scheme, the two trial finite element spaces are the nonconforming space of Crouzeix-Raviartfor the primal unknown u and the div-conformingspace of Raviart-Thomas for the flux φ. The two test spaces are the functions constant per cell both for the conservative and for the fluxequations.We prove an optimal second order error estimate for the box scheme and we emphasize the link between this scheme and the post-processing of Arnold and Brezzi of the classical mixed method.

Keywords

Box methodbox schememixed finite element methodPetrov-Galerkin methodfinite volume method.
Type
Research Article
Information
ESAIM: Mathematical Modelling and Numerical Analysis , Volume 34 , Issue 5 , September 2000 , pp. 1087 - 1106
Copyright
© EDP Sciences, SMAI, 2000

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Achchab, B., Agouzal, A., Baranger, J. and Maître, J-F., Estimateur d'erreur a posteriori hiérarchique. Application aux éléments finis mixtes. Numer. Math. 80 (1998) 159-179. CrossRef
Arnold, D.N. and Brezzi, F., Mixed and non-conforming finite elements methods: implementation, postprocessing and error estimates. RAIRO - Modél. Math. Anal. Numér. 19 (1985) 7-32. CrossRef
Babuska, I., Error-Bounds for Finite Elements Method. Numer. Math. 16 (1971) 322-333. CrossRef
Bank, R.E. and Rose, D.J., Some error estimates for the box method. SIAM J. Numer. Anal. 24 (1987) 777-787. CrossRef
Baranger, J., Maître, J.F. and Oudin, F., Connection between finite volume and mixed finite element methods. RAIRO - Modél. Math. Anal. Numér. 30 (1996) 445-465. CrossRef
C. Bernardi, C. Canuto and Y. Maday, Un problème variationnel abstrait. Application à une méthode de collocation pour les équations de Stokes. C. R. Acad. Sci. Paris, t.303, Série I 19 (1986) 971-974.
Bernardi, C., Canuto, C. and Maday, Y., Generalized inf-sup conditions for Chebyshev spectral approximation of the Stokes problem. SIAM J. Numer. Anal. 25 (1988) 1237-1271. CrossRef
D. Braess, Finite Elements. Cambridge Univ. Press (1997).
S.C. Brenner and L.R. Scott, The mathematical theory of finite element methods. Texts Appl. Math. 15 (1994) Springer, New-York.
F. Brezzi, On the existence, uniqueness and approximation of saddle-point problems, arising from lagrangian multipliers. RAIRO 8 (1974) R-2, 129-151.
F. Brezzi and M. Fortin, Mixed and Hybrid Finite Element Methods. Springer Series Comp. Math. 15, Springer Verlag, New-York (1991).
Brezzi, F., Douglas, J. and Marini, L.D., Two families of Mixed Finite Element for second order elliptic problems. Numer. Math. 47 (1985) 217-235. CrossRef
Cai, Z., Mandel, J. and McCormick, S., The finite volume element method for diffusion equations on general triangulations. SIAM J. Numer. Anal. 28 (1991) 392-402. CrossRef
F. Casier, H. Deconninck and C. Hirsch, A class of central bidiagonal schemes with implicit boundary conditions for the solution of Euler's equations. AIAA-83-0126 (1983).
J.J. Chattot, Box-schemes for First Order Partial Differential Equations. Adv. Comp. Fluid Dynamics, Gordon Breach Publ. (1995) 307-331.
J.J. Chattot, A Conservative Box-scheme for the Euler Equations. Int. J. Num. Meth. Fluids (to appear).
J.J. Chattot and S. Malet, A box-schemefor the Euler equations. Lect. Notes Math. 1270, Springer-Verlag, Berlin (1987) 82-99.
Coudière, Y., Vila, J-P. and Villedieu, P., Convergence rate of a finite volume scheme for a two dimensional convection-diffusion problem. Math. Model. Numer. 33 (1999) 493-516. CrossRef
B. Courbet, Schémas boîte en réseau triangulaire, Rapport technique 18/3446 EN (1992), ONERA, unpublished.
B. Courbet, Schémas à deux points pour la simulation numérique des écoulements, La Recherche Aérospatiale n°4 (1990) 21-46.
B. Courbet, Étude d'une famille de schémas boîtes à deux points et application à la dynamique des gaz monodimensionnelle, La Recherche Aérospatiale n°5 (1991) 31-44.
Courbet, B. and Croisille, J.P., Finite Volume Box Schemes on triangular meshes. Math. Model. Numer. 32 (1998) 631-649. CrossRef
J-P. Croisille, Finite Volume Box Schemes, in Proc. of the 2nd Int. Symp. on Finite Volume for Complex Applications. Hermes, Paris (1999).
M. Crouzeix and P.A. Raviart, Conforming and non conforming finite element methods for solving the stationary Stokes equations I. RAIRO 7 (1973) R-3, 33-76.
F. Dubois, Finite volumes and mixed Petrov-Galerkin finite elements; the unidimensional problem. Num. Meth. PDE (to appear).
R. Eymard, T. Gallouët and R. Herbin, Finite Volume Methods, in Handbook of Numerical Analysis, Ciarlet-Lions Eds. 5 (1997).
Fairweather, G. and Saylor, R.D., The reformulation and numerical solution of certain nonclassical initial-boundary value problems. SIAM J. Sci. Stat. Comput. 12 (1991) 127-144. CrossRef
Fezoui, L. and Stoufflet, B., A class of implicit upwind schemes for Euler equations on unstructured grids. J. Comp. Phys. 84 (1989) 174-206. CrossRef
V. Girault and P.A. Raviart, Finite Element Approximation of the Navier-Stokes equations. Lect. Notes Math. 749, Springer, Berlin (1979).
Hackbusch, W., On first and second order box schemes. Computing 41 (1989) 277-296. CrossRef
H.B. Keller, A new difference scheme for parabolic problems, Numerical solutions of partial differential equations, II, B. Hubbard Ed., Academic Press, New-York (1971) 327-350.
R.D. Lazarov, J.E. Pasciak and P.S. Vassilevski, Coupling mixed and finite volume discretizations of convection-diffusion-reaction equations on non-matching grids, in Proc. of the 2nd Int. Symp. on Finite Volume for Complex Applications, Hermes, Paris (1999).
Marini, L.D., An inexpensive method for the evaluation of the solution of the lowest order Raviart-Thomas mixed method. SIAM J. Numer. Anal. 22 (1985) 493-496. CrossRef
Meek, P.C. and Norbury, J., Nonlinear moving boundary problems and a Keller box scheme. SIAM J. Numer. Anal. 21 (1984) 883-893. CrossRef
Nicolaides, R.A., Existence, uniqueness and approximation for generalized saddle point problems. SIAM J. Numer. Anal. 19 (1982) 349-357. CrossRef
P.A. Raviart and J.M. Thomas, A mixed finite element method for 2nd order elliptic problems. Lect. Notes Math. 606, Springer-Verlag, Berlin (1977) 292-315.
Süli, E., Convergence of finite volume schemes for Poisson's equation on non-uniform meshes. SIAM J. Numer. Anal. 28 (1991) 1419-1430. CrossRef
Süli, E., The accuracy of cell vertex finite volume methods on quadrilateral meshes. Math. of Comp. 59 (1992) 359-382. CrossRef
Schmidt, T., Box Schemes on quadrilateral meshes. Computing 51 (1993) 271-292. CrossRef
J-M Thomas and D. Trujillo, Mixed Finite Volume methods. Int. J. Num. Meth. Eng. 45 (1999) to appear.
S.F. Wornom, Application of compact difference schemes to the conservative Euler equations for one-dimensional flows. NASA Tech. Mem. 83262 (1982).
Wornom, S.F. and Hafez, M.M., Implicit conservative schemes for the Euler equations. AIAA J. 24 (1986) 215-233. CrossRef
Younes, A., Mose, R., Ackerer, P. and Chavent, G., A new formulation of the Mixed Finite Element Method for solving elliptic and parabolic PDE. J. Comp. Phys. 149 (1999) 148-167. CrossRef