We study the turnpike phenomenon for optimal control problems with mean-field dynamics that are obtained as the limit N\rightarrow \infty$N\rightarrow \infty$ of systems governed by a large number N$N$ of ordinary differential equations. We show that the optimal control problems with large time horizons give rise to a turnpike structure of the optimal state and the optimal control. For the proof, we use the fact that the turnpike structure for the problems on the level of ordinary differential equations is preserved under the corresponding mean-field limit.

We study a system of nonlocal aggregation cross-diffusion PDEs that describe the evolution of opinion densities on a network. The PDEs are coupled with a system of ODEs that describe the time evolution of the agents on the network. Firstly, we apply the Deterministic Particle Approximation (DPA) method to the aforementioned system in order to prove the existence of solutions under suitable assumptions on the interactions between agents. Later on, we present an explicit model for opinion formation on an evolving network. The opinions evolve based on both the distance between the agents on the network and the ’attitude areas’, which depend on the distance between the agents’ opinions. The position of the agents on the network evolves based on the distance between the agents’ opinions. The goal is to study radicalisation, polarisation and fragmentation of the population while changing its open-mindedness and the radius of interaction.

In this paper, we derive the effective model describing a thin-domain flow with permeable boundary through which the fluid is injected into the domain. We start with incompressible Stokes system and perform the rigorous asymptotic analysis. Choosing the appropriate scaling for the injection leads to a compressible effective model. In this paper, we derive the effective model describing a thin-domain flow with permeable boundary through which the fluid is injected into the domain. We start with incompressible Stokes system and perform the rigorous asymptotic analysis. Choosing the appropriate scaling for the injection leads to a compressible effective model.

Flowering plants depend on some animals for pollination and contribute to nourish the animals in natural environments. We call these animals pollinators and build a plants-pollinators cooperative model with impulsive effect on a periodically evolving domain. Next, we define the ecological reproduction index for single plant model and plants-pollinators system, respectively, whose threshold dynamics, including the extinction, persistence and coexistence, is established by the method of upper and lower solutions. Theoretical analysis shows that a large domain evolution rate has a positive influence on the survival of pollinators whether or not the impulsive effect occurs, and the pulse eliminates the pollinators even when the evolution rate is high. Moreover, some selective numerical simulations are still performed to explain our theoretical results.

We consider heat or mass transport from a circular cylinder under a uniform crossflow at small Reynolds numbers, 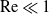\mathrm{Re}\ll 1$\mathrm{Re}\ll 1$. This problem has been thwarted in the past by limitations inherent in the classical analyses of the singular flow problem, which have used asymptotic expansions in inverse powers of 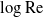\log \mathrm{Re}$\log \mathrm{Re}$. We here make use of the hybrid approximation of Kropinski, Ward & Keller [(1995) SIAM J. Appl. Math. 55, 1484], based upon a robust asymptotic expansion in powers of 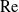\mathrm{Re}$\mathrm{Re}$. In that approximation, the “inner” streamfunction is provided by the product of a pre-factor 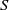S$S$, a slowly varying function of 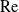\mathrm{Re}$\mathrm{Re}$, with a 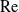\mathrm{Re}$\mathrm{Re}$-independent “canonical” solution of a simple mathematical form. The pre-factor, in turn, is determined as an implicit function of 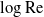\log \mathrm{Re}$\log \mathrm{Re}$ via asymptotic matching with a numerical solution of the nonlinear single-scaled “outer” problem, where the cylinder appears as a point singularity. We exploit the hybrid approximation to analyse the transport problem in the limit of large Péclet number, 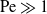\mathrm{Pe}\gg 1$\mathrm{Pe}\gg 1$. In that limit, transport is restricted to a narrow boundary layer about the cylinder surface – a province contained within the inner region of the flow problem. With 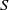S$S$ appearing as a parameter, a similarity solution is readily constructed for the boundary-layer problem. It provides the Nusselt number as 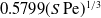0.5799(S\,\mathrm{Pe})^{1/3}$0.5799(S\,\mathrm{Pe})^{1/3}$. This asymptotic prediction is in remarkably close agreement with that of the numerical solution of the exact problem [Dennis, Hudson & Smith (1968) Phys. Fluids 11, 933] even for moderate 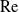\mathrm{Re}$\mathrm{Re}$-values.