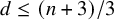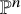1 Introduction
The problem of ‘counting’ subvarieties of a fixed projective variety has a long and illustrious history (see Section 1.4). One of the most successful modern theories for ‘counting curves’ is the Gromov–Witten (GW) theory. However, it is often the case that the virtual counts arising in GW theory do not answer the corresponding geometric enumerative questions. For example, the higher-genus GW invariants of
![]() ${\mathbb P}^3$
include many positive-dimensional contributions from the boundary of the moduli space of stable maps and therefore often fail to count smooth, embedded curves in
${\mathbb P}^3$
include many positive-dimensional contributions from the boundary of the moduli space of stable maps and therefore often fail to count smooth, embedded curves in
![]() ${\mathbb P}^3$
. For other targets, the question of whether the virtual counts are enumerative can be subtle.
${\mathbb P}^3$
. For other targets, the question of whether the virtual counts are enumerative can be subtle.
In this paper, we focus on a particular class of GW invariant, where the domain curve is fixed in moduli and required to pass through the maximum number of points. Given a smooth projective variety X over
![]() $\mathbb {C}$
, the fixed-domain GW invariant
$\mathbb {C}$
, the fixed-domain GW invariant
![]() $\text {GW}^{X,\text {fd}}_{g,\beta ,m}(p_1,\ldots ,p_m)$
is a virtual count of the number of maps
$\text {GW}^{X,\text {fd}}_{g,\beta ,m}(p_1,\ldots ,p_m)$
is a virtual count of the number of maps
![]() $f:(\widetilde {C},\widetilde {q}_1,\ldots ,\widetilde {q}_m)\to X$
where the stabilization
$f:(\widetilde {C},\widetilde {q}_1,\ldots ,\widetilde {q}_m)\to X$
where the stabilization
![]() $(C,q_1,\ldots ,q_m)$
of
$(C,q_1,\ldots ,q_m)$
of
![]() $(\widetilde {C},\widetilde {q}_1,\ldots ,\widetilde {q}_m)$
is a fixed pointed curve which is general in moduli,
$(\widetilde {C},\widetilde {q}_1,\ldots ,\widetilde {q}_m)$
is a fixed pointed curve which is general in moduli,
![]() $f(\widetilde {C})$
has class
$f(\widetilde {C})$
has class
![]() $\beta $
, and the morphism f satisfies
$\beta $
, and the morphism f satisfies
![]() $f(\widetilde {q}_i)=p_i$
for fixed general points
$f(\widetilde {q}_i)=p_i$
for fixed general points
![]() $p_1,\ldots ,p_m\in X$
. Such invariants are particularly interesting for the following reasons:
$p_1,\ldots ,p_m\in X$
. Such invariants are particularly interesting for the following reasons:
-
• A (nonprojective) Kähler manifold X might have very few complex analytic subvarieties, but GW invariants with point insertions make sense for any X.
-
• Due to the generality of the pointed curve
 $(C,q_1,\ldots ,q_m)$
and the points
$(C,q_1,\ldots ,q_m)$
and the points
 $\{p_{i}\}$
, we can hope to avoid the most pathological subvarieties of the moduli space of stable maps and therefore achieve transversality of intersections. Indeed, [Reference Lian and PandharipandeLP23, Speculation 12] asks whether, for every Fano variety X, the virtual count
$\{p_{i}\}$
, we can hope to avoid the most pathological subvarieties of the moduli space of stable maps and therefore achieve transversality of intersections. Indeed, [Reference Lian and PandharipandeLP23, Speculation 12] asks whether, for every Fano variety X, the virtual count
 $\text {GW}^{X,\text {fd}}_{g,\beta ,m}(p_1,\ldots ,p_m)$
is enumerative when the anticanonical degree is sufficiently large compared to the genus.
$\text {GW}^{X,\text {fd}}_{g,\beta ,m}(p_1,\ldots ,p_m)$
is enumerative when the anticanonical degree is sufficiently large compared to the genus. -
• Formulas for virtual counts
 $\text {GW}^{X,\text {fd}}_{g,\beta ,m}(p_1,\ldots ,p_m)$
are much simpler in many examples than arbitrary GW invariants; see, for example, [Reference Buch and PandharipandeBP21].
$\text {GW}^{X,\text {fd}}_{g,\beta ,m}(p_1,\ldots ,p_m)$
are much simpler in many examples than arbitrary GW invariants; see, for example, [Reference Buch and PandharipandeBP21].
In this paper, we solve the enumerativity question for fixed-domain GW invariants of several classes of complex Fano varieties. We give the first examples of Fano varieties for which the virtual counts
![]() $\text {GW}^{X,\text {fd}}_{g,\beta ,m}(p_1,\ldots ,p_m)$
fail to be enumerative (even in large degree), confuting [Reference Lian and PandharipandeLP23, Speculation 12]. We also give several new examples where enumerativity holds, including all smooth hypersurfaces in
$\text {GW}^{X,\text {fd}}_{g,\beta ,m}(p_1,\ldots ,p_m)$
fail to be enumerative (even in large degree), confuting [Reference Lian and PandharipandeLP23, Speculation 12]. We also give several new examples where enumerativity holds, including all smooth hypersurfaces in
![]() $\mathbb {P}^n$
of degree at most
$\mathbb {P}^n$
of degree at most
![]() $\frac {n+3}{3}$
. In practice, deciding whether
$\frac {n+3}{3}$
. In practice, deciding whether
![]() $\text {GW}^{X,\text {fd}}_{g,\beta ,m}(p_1,\ldots ,p_m)$
is enumerative comes down to the concrete geometric question of the existence of reducible pointed curves with stabilization isomorphic to
$\text {GW}^{X,\text {fd}}_{g,\beta ,m}(p_1,\ldots ,p_m)$
is enumerative comes down to the concrete geometric question of the existence of reducible pointed curves with stabilization isomorphic to
![]() $(C,q_1,\ldots ,q_m)$
and passing through the points
$(C,q_1,\ldots ,q_m)$
and passing through the points
![]() $p_1,\ldots ,p_m$
. In particular, we will not need to use any properties of the GW counts to verify asymptotic enumerativity.
$p_1,\ldots ,p_m$
. In particular, we will not need to use any properties of the GW counts to verify asymptotic enumerativity.
Remark 1.1. For certain targets X, the problem may also be considered in terms of the space of quasimaps, and the corresponding virtual counts can be related to the stable-map invariants via wall-crossing; see [Reference Ciocan-Fontanine, Kim and MaulikCFKM14, Reference Ciocan-Fontanine and KimCFK14]. Many of our arguments can be adapted equally well to the quasimap setting.
1.1 Fixed-domain GW invariants
Early computations of fixed-domain GW invariants were on Grassmannians; see, for instance, [Reference BertramBer94, Reference Bertram, Daskalopoulos and WentworthBDW96]. The Vafa–Intriligator formula, proven by Siebert–Tian [Reference Siebert and TianST97] in large degree and by Marian–Oprea in all degrees [Reference Marian and OpreaMO07], determines many virtual integrals of tautological classes on Quot schemes of trivial bundles on curves, and in particular determines the fixed-domain GW invariants of Grassmannians. More generally, descendent integrals on the space of stable quotients determine all GW invariants of Grassmannians [Reference Marian, Oprea and PandharipandeMOP11].
In the formulation we give below, the invariants
![]() $\text {GW}^{X,\text {fd}}_{g,\beta ,m}(p_1,\ldots ,p_m)$
were recently studied systematically by Buch and Pandharipande [Reference Buch and PandharipandeBP21] under the name ‘virtual Tevelev degrees’. The term ‘Tevelev degrees’ was introduced by Cela–Pandharipande–Schmitt [Reference Cela, Pandharipande and SchmittCPS22] after work of Tevelev [Reference TevelevTev20] on covers of
$\text {GW}^{X,\text {fd}}_{g,\beta ,m}(p_1,\ldots ,p_m)$
were recently studied systematically by Buch and Pandharipande [Reference Buch and PandharipandeBP21] under the name ‘virtual Tevelev degrees’. The term ‘Tevelev degrees’ was introduced by Cela–Pandharipande–Schmitt [Reference Cela, Pandharipande and SchmittCPS22] after work of Tevelev [Reference TevelevTev20] on covers of
![]() $\mathbb {P}^1$
. More recent calculations include partial results for Fano complete intersections [Reference CelaCel23] and blowups of projective spaces [Reference Cela and LianCL23, §4].
$\mathbb {P}^1$
. More recent calculations include partial results for Fano complete intersections [Reference CelaCel23] and blowups of projective spaces [Reference Cela and LianCL23, §4].
We now give a precise definition. For a smooth projective variety X, we let
![]() $N_{1}(X)_{\mathbb {Z}}$
denote the abelian group of numerical classes of curves and let
$N_{1}(X)_{\mathbb {Z}}$
denote the abelian group of numerical classes of curves and let
![]() $\mathrm {Nef}_{1}(X) \subset N_{1}(X)_{\mathbb {Z}} \otimes _{\mathbb {Z}} \mathbb {R}$
denote the nef cone of curves. Fix nonnegative integers
$\mathrm {Nef}_{1}(X) \subset N_{1}(X)_{\mathbb {Z}} \otimes _{\mathbb {Z}} \mathbb {R}$
denote the nef cone of curves. Fix nonnegative integers
![]() $g,m$
satisfying
$g,m$
satisfying
![]() $3g-3+m \ge 0$
; this guarantees that the moduli stack
$3g-3+m \ge 0$
; this guarantees that the moduli stack
![]() $\overline {\mathcal M}_{g,m}$
of stable curves of genus g with m marked points is well defined. Let
$\overline {\mathcal M}_{g,m}$
of stable curves of genus g with m marked points is well defined. Let
![]() $\beta \in N_{1}(X)_{\mathbb {Z}}$
be an effective curve class, and let
$\beta \in N_{1}(X)_{\mathbb {Z}}$
be an effective curve class, and let
![]() $\overline {\mathcal {M}}_{g,m}(X,\beta )$
denote the Kontsevich moduli stack of stable maps of genus g and class
$\overline {\mathcal {M}}_{g,m}(X,\beta )$
denote the Kontsevich moduli stack of stable maps of genus g and class
![]() $\beta $
with m marked points on X. We let
$\beta $
with m marked points on X. We let
![]() $\mathcal {M}_{g,m}(X,\beta ) \subset \overline {\mathcal M}_{g,m}(X,\beta )$
denote the open substack parametrizing stable maps with smooth domain.
$\mathcal {M}_{g,m}(X,\beta ) \subset \overline {\mathcal M}_{g,m}(X,\beta )$
denote the open substack parametrizing stable maps with smooth domain.
Consider the morphism
which combines the m-fold evaluation map with identification of the underlying curve. We would expect the fibers of this map to be finite precisely when the expected dimensions match, or equivalently, when
Definition 1.2. Given X, a fixed-domain triple is a triple
![]() $(g,\delta ,m)$
of nonnegative integers such that
$(g,\delta ,m)$
of nonnegative integers such that
If furthermore we have a numerical curve class
![]() $\beta \in \mathrm {Nef}_{1}(X)$
of anticanonical degree
$\beta \in \mathrm {Nef}_{1}(X)$
of anticanonical degree
![]() $\delta $
, the fixed-domain GW invariant
$\delta $
, the fixed-domain GW invariant
![]() $\text {GW}^{X,\text {fd}}_{g,\beta ,m}(p_1,\ldots ,p_m)$
is the degree of
$\text {GW}^{X,\text {fd}}_{g,\beta ,m}(p_1,\ldots ,p_m)$
is the degree of
![]() $\phi _{*}[\overline {\mathcal {M}}_{g,m}(X,\beta )]^{vir}$
as a multiple of the fundamental class
$\phi _{*}[\overline {\mathcal {M}}_{g,m}(X,\beta )]^{vir}$
as a multiple of the fundamental class
![]() $\overline {\mathcal {M}}_{g,m}\times X^{\times m}$
. One can more generally replace the
$\overline {\mathcal {M}}_{g,m}\times X^{\times m}$
. One can more generally replace the
![]() $p_i$
with other cohomology classes on X, but we will work only with point incidence conditions. We will henceforth suppress the points
$p_i$
with other cohomology classes on X, but we will work only with point incidence conditions. We will henceforth suppress the points
![]() $q_i,p_i$
from the notation and write simply
$q_i,p_i$
from the notation and write simply
![]() $\text {GW}^{X,\text {fd}}_{g,\beta ,m}$
.
$\text {GW}^{X,\text {fd}}_{g,\beta ,m}$
.
We say that the virtual count
![]() $\text {GW}^{X,\text {fd}}_{g,\beta ,m}$
is enumerative if a general fiber of
$\text {GW}^{X,\text {fd}}_{g,\beta ,m}$
is enumerative if a general fiber of
![]() $\phi $
consists of exactly
$\phi $
consists of exactly
![]() $\text {GW}^{X,\text {fd}}_{g,\beta ,m}$
smooth points, all of which correspond to maps
$\text {GW}^{X,\text {fd}}_{g,\beta ,m}$
smooth points, all of which correspond to maps
![]() $f:C\to X$
with irreducible (and hence smooth) domain. Note that this includes the possibility that the general fiber of
$f:C\to X$
with irreducible (and hence smooth) domain. Note that this includes the possibility that the general fiber of
![]() $\phi $
is empty and
$\phi $
is empty and
![]() ${\text {GW}^{X,\text {fd}}_{g,\beta ,m}=0}$
.
${\text {GW}^{X,\text {fd}}_{g,\beta ,m}=0}$
.
The virtual count
![]() $\text {GW}^{X,\text {fd}}_{g,\beta ,m}$
can fail to be enumerative if a general fiber of
$\text {GW}^{X,\text {fd}}_{g,\beta ,m}$
can fail to be enumerative if a general fiber of
![]() $\phi $
contains maps
$\phi $
contains maps
![]() $f:\widetilde {C}\to X$
where
$f:\widetilde {C}\to X$
where
![]() $\widetilde {C}$
is reducible, but the stable contraction of
$\widetilde {C}$
is reducible, but the stable contraction of
![]() $\widetilde {C}$
is a general point of
$\widetilde {C}$
is a general point of
![]() $\overline {{\mathcal M}}_{g,m}$
(and hence irreducible).
$\overline {{\mathcal M}}_{g,m}$
(and hence irreducible).
Example 1.3. Suppose that
![]() $X={\mathbb P}^n$
, and let
$X={\mathbb P}^n$
, and let
![]() $\beta $
be e times the class of a line, where
$\beta $
be e times the class of a line, where
If
![]() $e\ge m-1$
(or equivalently,
$e\ge m-1$
(or equivalently,
![]() $e\le ng$
), then there exist stable maps of the following form contributing to
$e\le ng$
), then there exist stable maps of the following form contributing to
![]() $\text {GW}^{X,\text {fd}}_{g,\beta ,m}$
. The domain curve consists of a smooth genus g curve C attached to
$\text {GW}^{X,\text {fd}}_{g,\beta ,m}$
. The domain curve consists of a smooth genus g curve C attached to
![]() $m-1$
rational tails. The point
$m-1$
rational tails. The point
![]() $p_m$
is on C and each of the rational tails contains one of the points
$p_m$
is on C and each of the rational tails contains one of the points
![]() $p_1,\ldots ,p_{m-1}$
. The map contracts C to
$p_1,\ldots ,p_{m-1}$
. The map contracts C to
![]() $p_m$
and maps the jth tail to a rational curve on
$p_m$
and maps the jth tail to a rational curve on
![]() ${\mathbb P}^n$
through
${\mathbb P}^n$
through
![]() $p_m$
and
$p_m$
and
![]() $p_j$
. (The condition that
$p_j$
. (The condition that
![]() $e \geq m-1$
guarantees that we can choose the degrees of the tails so that the total degree is e.) In particular, the virtual count
$e \geq m-1$
guarantees that we can choose the degrees of the tails so that the total degree is e.) In particular, the virtual count
![]() $\text {GW}^{X,\text {fd}}_{g,\beta ,m}$
fails to be enumerative.
$\text {GW}^{X,\text {fd}}_{g,\beta ,m}$
fails to be enumerative.
By definition, the geometric Tevelev degree
![]() $\text {Tev}^{X}_{g,\beta ,m}$
is the number of maps
$\text {Tev}^{X}_{g,\beta ,m}$
is the number of maps
![]() $f:C\to X$
in a general fiber of
$f:C\to X$
in a general fiber of
![]() $\phi $
with C smooth, assuming such a fiber is finite and reduced upon restriction to the open locus
$\phi $
with C smooth, assuming such a fiber is finite and reduced upon restriction to the open locus
![]() $\mathcal {M}_{g,m}(X,\beta )$
. Geometric Tevelev degrees, while having a more transparent definition, are often more difficult to compute than the corresponding GW invariants and at present are only fully understood for all curve classes when X is a projective space [Reference LianLia23b]. However, if the virtual count
$\mathcal {M}_{g,m}(X,\beta )$
. Geometric Tevelev degrees, while having a more transparent definition, are often more difficult to compute than the corresponding GW invariants and at present are only fully understood for all curve classes when X is a projective space [Reference LianLia23b]. However, if the virtual count
![]() $\text {GW}^{X,\text {fd}}_{g,\beta ,m}$
is enumerative, then
$\text {GW}^{X,\text {fd}}_{g,\beta ,m}$
is enumerative, then
![]() $\text {GW}^{X,\text {fd}}_{g,\beta ,m}=\text {Tev}^{X}_{g,\beta ,m}$
. According to our terminology, the converse is not necessarily true: It may happen that contributions to
$\text {GW}^{X,\text {fd}}_{g,\beta ,m}=\text {Tev}^{X}_{g,\beta ,m}$
. According to our terminology, the converse is not necessarily true: It may happen that contributions to
![]() $\text {GW}^{X,\text {fd}}_{g,\beta ,m}$
from curves of reducible domain exist, but all cancel upon integration against the virtual fundamental class; see Example 1.4.
$\text {GW}^{X,\text {fd}}_{g,\beta ,m}$
from curves of reducible domain exist, but all cancel upon integration against the virtual fundamental class; see Example 1.4.
Example 1.4. Suppose that
![]() $X={\mathbb P}^1\times {\mathbb P}^1$
, and let
$X={\mathbb P}^1\times {\mathbb P}^1$
, and let
![]() $\beta $
be the class of a
$\beta $
be the class of a
![]() $(e_1,e_2)$
-curve, where
$(e_1,e_2)$
-curve, where
and furthermore
![]() $m-1\le e_1<e_2$
. Note first that there are no maps
$m-1\le e_1<e_2$
. Note first that there are no maps
![]() $C\to {\mathbb P}^1\times {\mathbb P}^1$
in class
$C\to {\mathbb P}^1\times {\mathbb P}^1$
in class
![]() $\beta $
satisfying the conditions
$\beta $
satisfying the conditions
![]() $f(q_i)=p_i$
because the map
$f(q_i)=p_i$
because the map
![]() $C\to {\mathbb P}^1$
obtained by projection to the first factor would be required to satisfy
$C\to {\mathbb P}^1$
obtained by projection to the first factor would be required to satisfy
![]() $m>2e_1-g+1$
incidence conditions, which is impossible. Furthermore, we have
$m>2e_1-g+1$
incidence conditions, which is impossible. Furthermore, we have
![]() $\text {GW}^{X,\text {fd}}_{g,\beta ,m}=0$
by the GW product formula; see [Reference Buch and PandharipandeBP21, §2.2].
$\text {GW}^{X,\text {fd}}_{g,\beta ,m}=0$
by the GW product formula; see [Reference Buch and PandharipandeBP21, §2.2].
On the other hand, adapting the construction of Example 1.3 gives stable maps of
![]() $\overline {\mathcal {M}}_{g,m}(X,\beta )$
that map to a general point of
$\overline {\mathcal {M}}_{g,m}(X,\beta )$
that map to a general point of
![]() $\overline {\mathcal {M}}_{g,m}\times X^{\times m}$
. Thus, in our terminology, we say that
$\overline {\mathcal {M}}_{g,m}\times X^{\times m}$
. Thus, in our terminology, we say that
![]() $\text {GW}^{X,\text {fd}}_{g,\beta ,m}$
fails to be enumerative, despite the fact that it is equal to
$\text {GW}^{X,\text {fd}}_{g,\beta ,m}$
fails to be enumerative, despite the fact that it is equal to
![]() $\text {Tev}^{X}_{g,\beta ,m}$
.
$\text {Tev}^{X}_{g,\beta ,m}$
.
The main question we consider is:
Motivating Question 1.5. Let X be a Fano variety and fix a numerical curve class
![]() $\beta $
and nonnegative integers
$\beta $
and nonnegative integers
![]() $g,m$
satisfying
$g,m$
satisfying
![]() $3g-3+m \ge 0$
and
$3g-3+m \ge 0$
and
![]() $-K_{X} \cdot \beta + \dim (X)(1-g) = m \dim (X)$
. When is the fixed-domain GW invariant
$-K_{X} \cdot \beta + \dim (X)(1-g) = m \dim (X)$
. When is the fixed-domain GW invariant
![]() $\text {GW}^{X,\text {fd}}_{g,\beta ,m}$
enumerative?
$\text {GW}^{X,\text {fd}}_{g,\beta ,m}$
enumerative?
As we saw earlier in Example 1.3, one can only hope that
![]() $\text {GW}^{X,\text {fd}}_{g,\beta ,m}$
is enumerative when the number of points m (or equivalently, the anticanonical degree
$\text {GW}^{X,\text {fd}}_{g,\beta ,m}$
is enumerative when the number of points m (or equivalently, the anticanonical degree
![]() $\delta $
of the curve) is large compared to the genus of the underlying curve. Lian and Pandharipande [Reference Lian and PandharipandeLP23] speculate that for any Fano X, the virtual count
$\delta $
of the curve) is large compared to the genus of the underlying curve. Lian and Pandharipande [Reference Lian and PandharipandeLP23] speculate that for any Fano X, the virtual count
![]() $\text {GW}^{X,\text {fd}}_{g,\beta ,m}$
for a fixed-domain triple
$\text {GW}^{X,\text {fd}}_{g,\beta ,m}$
for a fixed-domain triple
![]() $(g,\delta ,m)$
is enumerative whenever
$(g,\delta ,m)$
is enumerative whenever
![]() $\delta $
is sufficiently large relative to g. This speculation is captured by the following definition:
$\delta $
is sufficiently large relative to g. This speculation is captured by the following definition:
Definition 1.6. We say X satisfies asymptotic enumerativity for a given genus g if, for all fixed-domain triples
![]() $(g,\delta ,m)$
with m sufficiently large (depending only on X and g), the virtual count
$(g,\delta ,m)$
with m sufficiently large (depending only on X and g), the virtual count
![]() $\text {GW}^{X,\text {fd}}_{g,\beta ,m}$
is enumerative.
$\text {GW}^{X,\text {fd}}_{g,\beta ,m}$
is enumerative.
Remark 1.7. The notion of asymptotic enumerativity differs from that of strong asymptotic enumerativity [Reference Cela and LianCL23, Definition 5] in that we do not require in genus 0 that
![]() $\text {GW}^{X,\text {fd}}_{0,\beta ,m}$
be enumerative for all fixed-domain triples
$\text {GW}^{X,\text {fd}}_{0,\beta ,m}$
be enumerative for all fixed-domain triples
![]() $(0,\delta ,m)$
.
$(0,\delta ,m)$
.
Asymptotic enumerativity has previously been verified in the following examples:
-
• X is a Grassmannian [Reference BertramBer94, Reference Bertram, Daskalopoulos and WentworthBDW96].
-
•
 $X=G/P$
is a homogeneous space [Reference Lian and PandharipandeLP23, Theorem 10].
$X=G/P$
is a homogeneous space [Reference Lian and PandharipandeLP23, Theorem 10]. -
• X is a hypersurface of degree d in
 ${\mathbb P}^n$
, where
${\mathbb P}^n$
, where
 $n-1>(d+1)(d-2)$
[Reference Lian and PandharipandeLP23, Theorem 11].
$n-1>(d+1)(d-2)$
[Reference Lian and PandharipandeLP23, Theorem 11]. -
•
 $X=\text {Bl}_{q}{\mathbb P}^n$
is the blowup of
$X=\text {Bl}_{q}{\mathbb P}^n$
is the blowup of
 ${\mathbb P}^n$
in a single point [Reference Cela and LianCL23, Theorem 23].
${\mathbb P}^n$
in a single point [Reference Cela and LianCL23, Theorem 23]. -
• X is a del Pezzo surface [Reference Cela and LianCL23, Theorem 24].
We disprove the speculation of [Reference Lian and PandharipandeLP23] by giving several examples of Fano varieties for which asymptotic enumerativity fails: certain Fano threefolds, hypersurfaces with a conical linear section and Fano projective bundles over
![]() $\mathbb {P}^n$
with sufficiently negative sections. We also give several new examples where asymptotic enumerativity holds: certain Fano threefolds and many Fano hypersurfaces.
$\mathbb {P}^n$
with sufficiently negative sections. We also give several new examples where asymptotic enumerativity holds: certain Fano threefolds and many Fano hypersurfaces.
1.2 Negative results
We present two families of examples of Fano varieties X for which asymptotic enumerativity fails. The first is Fano varieties which carry a ‘conical’ divisor.
Proposition 1.8. Let X be a smooth Fano variety of dimension N, Picard rank
![]() $1$
and Fano index r. Furthermore, assume that:
$1$
and Fano index r. Furthermore, assume that:
-
• X carries an irreducible divisor D and a point
 $p \in D$
such that every point of D is contained in an anticanonical line through p in D, and
$p \in D$
such that every point of D is contained in an anticanonical line through p in D, and -
• There is a positive integer
 $t\le \frac {N}{r}-1$
such that X carries a family of free rational curves of anticanonical degree
$t\le \frac {N}{r}-1$
such that X carries a family of free rational curves of anticanonical degree
 $tr$
.
$tr$
.
Then X fails to satisfy asymptotic enumerativity for all
![]() $g>0$
. If furthermore
$g>0$
. If furthermore
![]() $t<\frac {N}{r}-1$
, then X also fails to satisfy asymptotic enumerativity for
$t<\frac {N}{r}-1$
, then X also fails to satisfy asymptotic enumerativity for
![]() $g=0$
.
$g=0$
.
An example of a variety X satisfying the conditions of Proposition 1.8 for
![]() $g>0$
is a Fermat hypersurface X of degree
$g>0$
is a Fermat hypersurface X of degree
![]() $d\in \left [\frac {n+3}{2},n-1\right ]$
in
$d\in \left [\frac {n+3}{2},n-1\right ]$
in
![]() $\mathbb {P}^{n}$
when
$\mathbb {P}^{n}$
when
![]() $n\ge 4$
. More generally, one can apply Proposition 1.8 to any hypersurface of degree
$n\ge 4$
. More generally, one can apply Proposition 1.8 to any hypersurface of degree
![]() $d\in \left [\frac {n+3}{2},n-1\right ]$
which admits a hyperplane section which is a cone over a lower-dimensional hypersurface of the same degree. See Examples 3.2 and 3.4 for more details.
$d\in \left [\frac {n+3}{2},n-1\right ]$
which admits a hyperplane section which is a cone over a lower-dimensional hypersurface of the same degree. See Examples 3.2 and 3.4 for more details.
Our second family of examples is certain Fano projective bundles X over projective space. When X is defined by a vector bundle which is very unstable, then certain numerical classes on X cannot possibly be represented by free rational curves with balanced restricted tangent bundle. The following result ‘upgrades’ this observation to a failure of asymptotic enumerativity.
Proposition 1.9. Fix positive integers
![]() $n,r$
satisfying
$n,r$
satisfying
![]() $n> r+1$
. Consider the vector bundle
$n> r+1$
. Consider the vector bundle
![]() $\mathcal {E} = \bigoplus _{i=0}^{r} \mathcal {O}(a_{i})$
on
$\mathcal {E} = \bigoplus _{i=0}^{r} \mathcal {O}(a_{i})$
on
![]() $\mathbb {P}^{n-r}$
, where
$\mathbb {P}^{n-r}$
, where
![]() $a_{0}=0$
and
$a_{0}=0$
and
![]() $a_{i} \geq 0$
for
$a_{i} \geq 0$
for
![]() $i \geq 1$
. Suppose that
$i \geq 1$
. Suppose that
 $$ \begin{align*} \sum_{i=1}^{r} a_i \leq n-r \end{align*} $$
$$ \begin{align*} \sum_{i=1}^{r} a_i \leq n-r \end{align*} $$
so that X is Fano, and suppose further that
 $$ \begin{align*} \sum_{i=1}^{r} a_i \geq 2. \end{align*} $$
$$ \begin{align*} \sum_{i=1}^{r} a_i \geq 2. \end{align*} $$
Then asymptotic enumerativity fails for the projective bundle
![]() $X = \mathbb {P}_{\mathbb {P}^{n-r}}(\mathcal {E})$
in every genus.
$X = \mathbb {P}_{\mathbb {P}^{n-r}}(\mathcal {E})$
in every genus.
1.3 Positive results
We also identify several new situations in which asymptotic enumerativity holds. The first addresses asymptotic enumerativity for a Fano threefold X. We show that asymptotic enumerativity is only obstructed by the presence of certain divisors
![]() $Y \subset X$
.
$Y \subset X$
.
Theorem 1.10. Let X be a smooth Fano threefold. Suppose that there is no divisor
![]() $Y \subset X$
that is swept out by anticanonical lines. Then X satisfies asymptotic enumerativity for every genus g.
$Y \subset X$
that is swept out by anticanonical lines. Then X satisfies asymptotic enumerativity for every genus g.
Example 1.11. Theorem 1.10 shows that smooth cubic threefolds satisfy asymptotic enumerativity. Smooth cubic hypersurfaces of dimension
![]() $\geq 5$
satisfy asymptotic enumerativity by [Reference Lian and PandharipandeLP23, Theorem 11]. However, the case of cubic hypersurfaces of dimension
$\geq 5$
satisfy asymptotic enumerativity by [Reference Lian and PandharipandeLP23, Theorem 11]. However, the case of cubic hypersurfaces of dimension
![]() $4$
is still open.
$4$
is still open.
Theorem 4.3 is a stronger version of Theorem 1.10 which includes more information about the types of curves which can violate asymptotic enumerativity. When a smooth Fano threefold X carries a divisor Y swept out by anticanonical lines, it is usually possible to combine Theorem 4.3 with a geometric argument to determine whether one can use this divisor to violate asymptotic enumerativity. We do not prove a precise statement in this direction but instead give several examples; see Example 4.4, Example 4.5, Example 4.6 and Example 4.7.
Remark 1.12. The Fujita invariant of a polarized variety
![]() $(Y,L)$
compares the negativity of the canonical divisor against the positivity of L (see Definition 2.5). If a Fano variety X admits a subvariety Y swept out by a family of rational curves whose dimension is larger than expected, then [Reference Lehmann and TanimotoLT19, Theorem 1.1] shows that
$(Y,L)$
compares the negativity of the canonical divisor against the positivity of L (see Definition 2.5). If a Fano variety X admits a subvariety Y swept out by a family of rational curves whose dimension is larger than expected, then [Reference Lehmann and TanimotoLT19, Theorem 1.1] shows that
![]() $(Y,-K_{X})$
has Fujita invariant larger than
$(Y,-K_{X})$
has Fujita invariant larger than
![]() $1$
. Conjecturally, the reverse implication is also true.
$1$
. Conjecturally, the reverse implication is also true.
As demonstrated in the proof of Theorem 1.10, the condition on Y in Theorem 1.10 is the same as requiring that the Fujita invariant of Y with respect to
![]() $-K_{X}$
is at least
$-K_{X}$
is at least
![]() $2$
. More generally, we expect that asymptotic enumerativity will often fail for Fano varieties X which carry a subvariety with large Fujita invariant (which conjecturally admit ‘too many’ rational curves). Unfortunately, it is too much to hope for an implication in either direction. Example 4.7 gives an example of a smooth Fano threefold which satisfies asymptotic enumerativity in every genus even though it carries a divisor of Fujita invariant
$2$
. More generally, we expect that asymptotic enumerativity will often fail for Fano varieties X which carry a subvariety with large Fujita invariant (which conjecturally admit ‘too many’ rational curves). Unfortunately, it is too much to hope for an implication in either direction. Example 4.7 gives an example of a smooth Fano threefold which satisfies asymptotic enumerativity in every genus even though it carries a divisor of Fujita invariant
![]() $2$
. Conversely, Example 3.6 shows that one can construct curves which violate asymptotic enumerativity even when no irreducible component of the curve lies on a subvariety Y with Fujita invariant
$2$
. Conversely, Example 3.6 shows that one can construct curves which violate asymptotic enumerativity even when no irreducible component of the curve lies on a subvariety Y with Fujita invariant
![]() $>1$
.
$>1$
.
Our final result builds off of [Reference Lian and PandharipandeLP23] to prove new examples of asymptotic enumerativity for hypersurfaces.
Theorem 1.13. Suppose X is a smooth hypersurface of degree d in
![]() $\mathbb {P}^n$
such that
$\mathbb {P}^n$
such that
-
(1)
 $d \leq n-2$
and X is general, or
$d \leq n-2$
and X is general, or -
(2)
 $d \leq (n+3)/3$
.
$d \leq (n+3)/3$
.
Then, X satisfies asymptotic enumerativity for every genus g.
In particular, we obtain transversality in the geometric calculations of [Reference LianLia23a] when
![]() $d\le (n+2)/2$
and X in addition satisfies (1) or (2). Note that the linear bound (2) is a significant improvement over the quadratic bound of [Reference Lian and PandharipandeLP23, Theorem 11]. We expect that the condition in (2) can be weakened to ‘
$d\le (n+2)/2$
and X in addition satisfies (1) or (2). Note that the linear bound (2) is a significant improvement over the quadratic bound of [Reference Lian and PandharipandeLP23, Theorem 11]. We expect that the condition in (2) can be weakened to ‘
![]() $d \leq \frac {n+1}{2}$
.’ Our proof method could conceivably extend to this larger degree range, but it would require solving a conjecture concerning the dimension of the space of nonfree lines for the corresponding hypersurfaces.
$d \leq \frac {n+1}{2}$
.’ Our proof method could conceivably extend to this larger degree range, but it would require solving a conjecture concerning the dimension of the space of nonfree lines for the corresponding hypersurfaces.
1.4 History
For a compact Kähler manifold, what effective complex analytic cycles can we ‘count’, and are those ‘counts’ invariant under deformation? In the special case of complex projective manifolds, this is one of the oldest problems in algebraic geometry, dating back at least 150 years to work of Steiner, Chasles, de Jonquiéres and, especially, Schubert [Reference Eisenbud and HarrisEH16]. Hilbert’s search for a rigorous foundation for Schubert’s (unpublished) methods for counting cycles eventually led to the invention of the cohomology ring [Reference KleimanKle76]. The modern perspective on ‘counting’ cycles of complex dimension
![]() $1$
led to the invention of the quantum cohomology ring whose ring product is a deformation of the usual cup product with ‘corrections’ coming from GW invariants. In particular, these are invariant under complex deformation and even under symplectic deformation. However, this does not completely solve the problem of counting cycles, since GW invariants allow contributions that are classically prohibited, for example, GW invariants can be fractional and even negative whereas true ‘counts’ are nonnegative integers. This leads to a sharper question: When are GW invariants of a Kähler manifold enumerative?
$1$
led to the invention of the quantum cohomology ring whose ring product is a deformation of the usual cup product with ‘corrections’ coming from GW invariants. In particular, these are invariant under complex deformation and even under symplectic deformation. However, this does not completely solve the problem of counting cycles, since GW invariants allow contributions that are classically prohibited, for example, GW invariants can be fractional and even negative whereas true ‘counts’ are nonnegative integers. This leads to a sharper question: When are GW invariants of a Kähler manifold enumerative?
Recall a Kähler manifold is a connected, compact differentiable manifold M whose (real) dimension is even, say
![]() $2n$
, together with a symplectic form
$2n$
, together with a symplectic form
![]() $\omega $
(real, closed, everywhere nondegenerate differential
$\omega $
(real, closed, everywhere nondegenerate differential
![]() $2$
-form) with class
$2$
-form) with class
![]() $[\omega ]\in H^2(M;\mathbb {R})$
and an
$[\omega ]\in H^2(M;\mathbb {R})$
and an
![]() $\omega $
-compatible complex structure J, that is, the bilinear form
$\omega $
-compatible complex structure J, that is, the bilinear form
![]() $\omega (\bullet , J(\bullet ))$
is everywhere symmetric and positive definite. There are many cohomology classes associated to
$\omega (\bullet , J(\bullet ))$
is everywhere symmetric and positive definite. There are many cohomology classes associated to
![]() $(M,\omega ,J)$
that are invariant under complex deformations and even under symplectic deformations of
$(M,\omega ,J)$
that are invariant under complex deformations and even under symplectic deformations of
![]() $\omega $
, for example, the Chern classes
$\omega $
, for example, the Chern classes
![]() $c_i(T_{M,J})$
of the holomorphic tangent bundle for
$c_i(T_{M,J})$
of the holomorphic tangent bundle for
![]() $i=0,\dots ,n$
and thus also all polynomials in these classes. In fact, these are all of Hodge
$i=0,\dots ,n$
and thus also all polynomials in these classes. In fact, these are all of Hodge
![]() $(p,p)$
-type, so potentially in the image of the cycle class map so perhaps arising from cycles that we can count. In fact, there are many Kähler manifolds where the only connected, closed analytic cycles are M and points. By contrast, note that the real
$(p,p)$
-type, so potentially in the image of the cycle class map so perhaps arising from cycles that we can count. In fact, there are many Kähler manifolds where the only connected, closed analytic cycles are M and points. By contrast, note that the real
![]() $(1,1)$
-class
$(1,1)$
-class
![]() $[\omega ]$
is almost never invariant under symplectic deformations, yet it is always the image of an effective
$[\omega ]$
is almost never invariant under symplectic deformations, yet it is always the image of an effective
![]() $\mathbb {Q}$
-cycle if this
$\mathbb {Q}$
-cycle if this
![]() $(1,1)$
-class is in
$(1,1)$
-class is in
![]() $H^2(M;\mathbb {Q})$
by the Kodaira embedding theorem. We can finesse this by restricting to Kähler manifolds
$H^2(M;\mathbb {Q})$
by the Kodaira embedding theorem. We can finesse this by restricting to Kähler manifolds
![]() $(M,\omega ,J)$
such that
$(M,\omega ,J)$
such that
![]() $[\omega ]$
is a specified positive rational multiple of
$[\omega ]$
is a specified positive rational multiple of
![]() $c_1(T_{M,J})$
, that is, Fano manifolds, or such that
$c_1(T_{M,J})$
, that is, Fano manifolds, or such that
![]() $[\omega ]$
is a specified negative rational multiple of
$[\omega ]$
is a specified negative rational multiple of
![]() $c_1(T_{M,J})$
, that is, manifolds of general type with ample canonical divisor class.
$c_1(T_{M,J})$
, that is, manifolds of general type with ample canonical divisor class.
In [Reference GromovGro85], Gromov showed that often there are complex analytic subvarieties of complex dimension
![]() $1$
, and these J-holomorphic curves can often be ‘counted’ to produce a rational number that is independent of symplectic deformations. Over the next decade, with much input from Witten and other physicists, this developed into the GW theory. The definition within algebraic geometry applies to every smooth projective variety X defined over an arbitrary field k (of arbitrary characteristic). The foundational papers for GW invariants in algebraic geometry are [Reference KontsevichKon95], [Reference Behrend and FantechiBF97], [Reference Behrend and ManinBM96], [Reference BehrendBeh97], [Reference Li and TianLT98] and [Reference PomaPom15]. There are excellent surveys of the constructions in algebraic geometry: [Reference Fulton and PandharipandeFP97] and [Reference Cox and KatzCK99]. (For constructions in symplectic side, we refer to [Reference RuanRua96, Reference Ruan and TianRT95].)
$1$
, and these J-holomorphic curves can often be ‘counted’ to produce a rational number that is independent of symplectic deformations. Over the next decade, with much input from Witten and other physicists, this developed into the GW theory. The definition within algebraic geometry applies to every smooth projective variety X defined over an arbitrary field k (of arbitrary characteristic). The foundational papers for GW invariants in algebraic geometry are [Reference KontsevichKon95], [Reference Behrend and FantechiBF97], [Reference Behrend and ManinBM96], [Reference BehrendBeh97], [Reference Li and TianLT98] and [Reference PomaPom15]. There are excellent surveys of the constructions in algebraic geometry: [Reference Fulton and PandharipandeFP97] and [Reference Cox and KatzCK99]. (For constructions in symplectic side, we refer to [Reference RuanRua96, Reference Ruan and TianRT95].)
A ‘curve class’
![]() $\beta $
on X can either be interpreted as an element in
$\beta $
on X can either be interpreted as an element in
![]() $H^{2n-2}(X)$
for an appropriate Weil cohomology theory or, more often, as an element in the finitely generated group
$H^{2n-2}(X)$
for an appropriate Weil cohomology theory or, more often, as an element in the finitely generated group
![]() $N_1(X)_{\mathbb {Z}}:=\text {Hom}_{\mathbb {Z}-\text {mod}}(\text {Pic}(X)/\text {Pic}^0(X),\mathbb {Z})$
. For every integer
$N_1(X)_{\mathbb {Z}}:=\text {Hom}_{\mathbb {Z}-\text {mod}}(\text {Pic}(X)/\text {Pic}^0(X),\mathbb {Z})$
. For every integer
![]() $g\geq 0$
, for every integer
$g\geq 0$
, for every integer
![]() $m\geq 0$
, and for every curve class
$m\geq 0$
, and for every curve class
![]() $\beta $
, there is a (homological) algebraic cycle class (with
$\beta $
, there is a (homological) algebraic cycle class (with
![]() $\mathbb {Q}$
-coefficients),
$\mathbb {Q}$
-coefficients),
where
![]() $d=d^{X,\beta }_{g,m}$
is the virtual dimension
$d=d^{X,\beta }_{g,m}$
is the virtual dimension
and where
![]() $\mathfrak {M}_{g,m}$
is the Artin stack of genus-g, m-pointed, prestable curves. This Artin stack is smooth of dimension
$\mathfrak {M}_{g,m}$
is the Artin stack of genus-g, m-pointed, prestable curves. This Artin stack is smooth of dimension
![]() $3g-3+m$
. Thus, for (cohomological) classes
$3g-3+m$
. Thus, for (cohomological) classes
![]() $\gamma _i$
of (complex) codimensions
$\gamma _i$
of (complex) codimensions
![]() $d_i$
on X for
$d_i$
on X for
![]() $i=1,\dots ,m$
, and for a (cohomological) class
$i=1,\dots ,m$
, and for a (cohomological) class
![]() $\lambda $
of (complex) codimension e on
$\lambda $
of (complex) codimension e on
![]() $\mathfrak {M}_{g,m}$
, the cap product pairing of the homological cycle class
$\mathfrak {M}_{g,m}$
, the cap product pairing of the homological cycle class
![]() $GW^{X,\beta }_{g,m}$
against the cohomological classes gives an associated number,
$GW^{X,\beta }_{g,m}$
against the cohomological classes gives an associated number,
which is zero unless the sum
![]() $d_1+\dots + d_m + e$
equals
$d_1+\dots + d_m + e$
equals
![]() $d^{X,\beta }_{g,m}$
. This is the typical formulation of GW invariants: as a functional on the set of
$d^{X,\beta }_{g,m}$
. This is the typical formulation of GW invariants: as a functional on the set of
![]() $m+1$
-tuples of cohomological classes.
$m+1$
-tuples of cohomological classes.
The cycle class
![]() $GW^{X,\beta }_{g,m}$
is the proper pushforward with respect to a regular
$GW^{X,\beta }_{g,m}$
is the proper pushforward with respect to a regular
![]() $1$
-morphism of Artin stacks
$1$
-morphism of Artin stacks
of a virtual fundamental class
Here,
![]() $\overline {\mathcal {M}}_{g,m}(X,\beta )$
is an Artin stack with finite diagonal (in characteristic
$\overline {\mathcal {M}}_{g,m}(X,\beta )$
is an Artin stack with finite diagonal (in characteristic
![]() $0$
it is a Deligne–Mumford stack). It parametrizes isomorphism classes of flat families of genus-g, m-pointed stable maps
$0$
it is a Deligne–Mumford stack). It parametrizes isomorphism classes of flat families of genus-g, m-pointed stable maps
![]() $(u: \widetilde {C} \to X,\widetilde {q}_1,\dots ,\widetilde {q}_m)$
to X from a connected, proper, reduced, at-worst-nodal curve
$(u: \widetilde {C} \to X,\widetilde {q}_1,\dots ,\widetilde {q}_m)$
to X from a connected, proper, reduced, at-worst-nodal curve
![]() $\widetilde {C}$
of arithmetic genus g with m specified (rational) points
$\widetilde {C}$
of arithmetic genus g with m specified (rational) points
![]() $\widetilde {q}_1,\dots ,\widetilde {q}_m$
contained in the smooth locus of
$\widetilde {q}_1,\dots ,\widetilde {q}_m$
contained in the smooth locus of
![]() $\widetilde {C}$
, and with a specified morphism
$\widetilde {C}$
, and with a specified morphism
![]() $u:\widetilde {C}\to X$
such that the log dualizing sheaf
$u:\widetilde {C}\to X$
such that the log dualizing sheaf
![]() $\omega _{\widetilde {C}}(\underline {\widetilde {q}}_1+\dots +\underline {\widetilde {q}}_m)$
is u-ample. The
$\omega _{\widetilde {C}}(\underline {\widetilde {q}}_1+\dots +\underline {\widetilde {q}}_m)$
is u-ample. The
![]() $1$
-morphism
$1$
-morphism
![]() $\Phi $
gives the stabilization of the m-pointed, prestable curve
$\Phi $
gives the stabilization of the m-pointed, prestable curve
![]() $(\widetilde {C},\widetilde {q}_1,\dots ,\widetilde {q}_m)$
, and
$(\widetilde {C},\widetilde {q}_1,\dots ,\widetilde {q}_m)$
, and
![]() $\text {ev}$
gives the m-tuple
$\text {ev}$
gives the m-tuple
![]() $(u(\widetilde {q}_1),\dots ,u(\widetilde {q}_m))$
.
$(u(\widetilde {q}_1),\dots ,u(\widetilde {q}_m))$
.
In particular, primary GW invariants are those with
![]() $\lambda $
equal to
$\lambda $
equal to
![]() $1$
. When also each class
$1$
. When also each class
![]() $\gamma _i$
is the Poincaré dual of the class of a closed subscheme
$\gamma _i$
is the Poincaré dual of the class of a closed subscheme
![]() $Z_i$
of X with pure dimension
$Z_i$
of X with pure dimension
![]() $d_i$
, then the cap product above is the pushforward of a
$d_i$
, then the cap product above is the pushforward of a
![]() $0$
-cycle inside the closed substack
$0$
-cycle inside the closed substack
![]() $\text {ev}^{-1}(Z_1\times \dots \times Z_m) \subset \overline {\mathcal {M}}_{g,m}(X,\beta )$
parameterizing stable maps with
$\text {ev}^{-1}(Z_1\times \dots \times Z_m) \subset \overline {\mathcal {M}}_{g,m}(X,\beta )$
parameterizing stable maps with
![]() $u(\widetilde {q}_i)$
contained in
$u(\widetilde {q}_i)$
contained in
![]() $Z_i$
. When this closed substack is a disjoint union (possibly empty) of points, then the GW invariant is enumerative: The GW invariant equals the number of stable maps mapping each marked point
$Z_i$
. When this closed substack is a disjoint union (possibly empty) of points, then the GW invariant is enumerative: The GW invariant equals the number of stable maps mapping each marked point
![]() $p_i$
into
$p_i$
into
![]() $Z_i$
.
$Z_i$
.
Notice that the expected dimension is negative if
![]() $\langle c_1(T_X),\beta \rangle $
is negative and we replace
$\langle c_1(T_X),\beta \rangle $
is negative and we replace
![]() $\beta $
by a suitably positive multiple
$\beta $
by a suitably positive multiple
![]() $e\beta $
of the curve class. For this reason, most enumerative results are proved under the hypothesis that
$e\beta $
of the curve class. For this reason, most enumerative results are proved under the hypothesis that
![]() $\langle c_1(T_X),\beta \rangle $
is positive for all nonzero, effective curve classes
$\langle c_1(T_X),\beta \rangle $
is positive for all nonzero, effective curve classes
![]() $\beta $
: this is conjecturally equivalent to the condition that X is Fano.
$\beta $
: this is conjecturally equivalent to the condition that X is Fano.
Some of the most striking examples of enumerativity are the oldest: For example, every smooth cubic hypersurface in
![]() $\mathbb {P}^3$
contains precisely 27 lines. One can leverage this into proving enumerativity for genus
$\mathbb {P}^3$
contains precisely 27 lines. One can leverage this into proving enumerativity for genus
![]() $0$
curves on cubic surfaces (and del Pezzo manifolds more generally) of higher anticanonical degree, for example, [Reference Göttsche and PandharipandeGP98]. Combining techniques from the Mori program with techniques (particularly deformation theory) introduced for GW theory, there are now many enumerativity theorems for genus
$0$
curves on cubic surfaces (and del Pezzo manifolds more generally) of higher anticanonical degree, for example, [Reference Göttsche and PandharipandeGP98]. Combining techniques from the Mori program with techniques (particularly deformation theory) introduced for GW theory, there are now many enumerativity theorems for genus
![]() $0$
GW invariants on Fano manifolds: for example, [Reference ThomsenTho98, Reference Kim and PandharipandeKP01, Reference Harris, Roth and StarrHRS04, Reference Beheshti and KumarBK13, Reference Riedl and YangRY19, Reference BourquiBou16, Reference CastravetCas04, Reference TestaTes09, Reference Coskun and StarrCS09, Reference Lehmann and TanimotoLT19, Reference Lehmann and TanimotoLT21, Reference Lehmann and TanimotoLT24, Reference Lehmann and TanimotoLT22, Reference Beheshti, Lehmann, Riedl and TanimotoBLRT22, Reference Shimizu and TanimotoST22, Reference Burke and JovinellyBJ22, Reference OkamuraOka24].
$0$
GW invariants on Fano manifolds: for example, [Reference ThomsenTho98, Reference Kim and PandharipandeKP01, Reference Harris, Roth and StarrHRS04, Reference Beheshti and KumarBK13, Reference Riedl and YangRY19, Reference BourquiBou16, Reference CastravetCas04, Reference TestaTes09, Reference Coskun and StarrCS09, Reference Lehmann and TanimotoLT19, Reference Lehmann and TanimotoLT21, Reference Lehmann and TanimotoLT24, Reference Lehmann and TanimotoLT22, Reference Beheshti, Lehmann, Riedl and TanimotoBLRT22, Reference Shimizu and TanimotoST22, Reference Burke and JovinellyBJ22, Reference OkamuraOka24].
Returning to an arbitrary Kähler manifold
![]() $X=(M,J)$
, as mentioned before, the only connected complex analytic subvarieties might be M and points. Thus, the only primary GW invariants for which we can always discuss enumerativity are the primary GW invariants where every
$X=(M,J)$
, as mentioned before, the only connected complex analytic subvarieties might be M and points. Thus, the only primary GW invariants for which we can always discuss enumerativity are the primary GW invariants where every
![]() $\gamma _i$
equals the Poincaré dual of the class of a point. Of course the invariant is zero for degree reasons unless
$\gamma _i$
equals the Poincaré dual of the class of a point. Of course the invariant is zero for degree reasons unless
Recall that we restrict in this paper to GW invariants with point insertions where we also fix the isomorphism type of the underlying stable curve. Just as for all GW invariants, there are many cases where the virtual count
![]() $\text {GW}^{X,\text {fd}}_{g,\beta ,m}$
is not enumerative. What is remarkable is that there are many cases where these counts are enumerative. For example, it had essentially been understood that fixed-domain GW invariants of Grassmannians, as computed (in various guises) in [Reference BertramBer94, Reference Bertram, Daskalopoulos and WentworthBDW96, Reference Siebert and TianST97, Reference Marian and OpreaMO07, Reference Marian, Oprea and PandharipandeMOP11], give geometric counts of curves when the anticanonical degree is sufficiently large. This philosophy was revisited for more general targets in [Reference Lian and PandharipandeLP23]. Equally remarkable, the proofs are asymptotic in the anticanonical degree without any careful analysis of a ‘base case.’ This finally brings us to our motivating question: For which Fano manifolds are the virtual counts
$\text {GW}^{X,\text {fd}}_{g,\beta ,m}$
is not enumerative. What is remarkable is that there are many cases where these counts are enumerative. For example, it had essentially been understood that fixed-domain GW invariants of Grassmannians, as computed (in various guises) in [Reference BertramBer94, Reference Bertram, Daskalopoulos and WentworthBDW96, Reference Siebert and TianST97, Reference Marian and OpreaMO07, Reference Marian, Oprea and PandharipandeMOP11], give geometric counts of curves when the anticanonical degree is sufficiently large. This philosophy was revisited for more general targets in [Reference Lian and PandharipandeLP23]. Equally remarkable, the proofs are asymptotic in the anticanonical degree without any careful analysis of a ‘base case.’ This finally brings us to our motivating question: For which Fano manifolds are the virtual counts
![]() $\text {GW}^{X,\text {fd}}_{g,\beta ,m}$
asymptotically enumerative?
$\text {GW}^{X,\text {fd}}_{g,\beta ,m}$
asymptotically enumerative?
2 Background
We recall some basic definitions regarding Fano varieties and expected dimension.
Definition 2.1. A smooth projective variety X of positive dimension is a Fano manifold of Picard rank one if every ample divisor class is
![]() $\mathbb {Q}$
-numerically equivalent to a positive multiple of the first Chern class of the tangent bundle,
$\mathbb {Q}$
-numerically equivalent to a positive multiple of the first Chern class of the tangent bundle,
![]() $c_1(T_X) = -K_X$
. The Fano index is the largest positive integer r such that
$c_1(T_X) = -K_X$
. The Fano index is the largest positive integer r such that
![]() $c_1(T_X)$
equals r times an integral divisor class.
$c_1(T_X)$
equals r times an integral divisor class.
Example 2.2. For every
![]() $n\geq 3$
, a smooth codimension-c intersection in
$n\geq 3$
, a smooth codimension-c intersection in
![]() $\mathbb {P}^{n+c}$
of c hypersurfaces of degrees
$\mathbb {P}^{n+c}$
of c hypersurfaces of degrees
![]() $(d_1,\dots ,d_c)$
is a Fano manifold of Picard rank one if and only if
$(d_1,\dots ,d_c)$
is a Fano manifold of Picard rank one if and only if
![]() $d_1 + \dots + d_c\leq n+c$
, in which case the Fano index equals
$d_1 + \dots + d_c\leq n+c$
, in which case the Fano index equals
![]() $(n+c+1)-(d_1+\dots +d_c)$
.
$(n+c+1)-(d_1+\dots +d_c)$
.
For morphisms u to a smooth projective variety Z from local complete intersection curves C of arithmetic genus g such that the morphism has a finite automorphism group, there is a deformation-obstruction theory that gives an isomorphism of the completion of the local ring of the moduli space of such maps at the point corresponding to
![]() $(u:C\to Z)$
with the quotient of a power series ring of dimension
$(u:C\to Z)$
with the quotient of a power series ring of dimension
![]() $h^0$
by an ideal generated by
$h^0$
by an ideal generated by
![]() $h^1$
elements, for integers
$h^1$
elements, for integers
![]() $h^0$
and
$h^0$
and
![]() $h^1$
that satisfy the identity,
$h^1$
that satisfy the identity,
By Krull’s Hauptidealsatz, this is a lower bound for the dimension of the moduli space near
![]() $(u:C\to Z)$
, and the moduli space is locally a complete intersection (as a Deligne–Mumford stack) if this lower bound equals the dimension.
$(u:C\to Z)$
, and the moduli space is locally a complete intersection (as a Deligne–Mumford stack) if this lower bound equals the dimension.
Definition 2.3. The difference
![]() $h^0-h^1$
above is the virtual dimension or expected dimension of the moduli space near the point
$h^0-h^1$
above is the virtual dimension or expected dimension of the moduli space near the point
![]() $(u:C\to Z)$
.
$(u:C\to Z)$
.
The following notion plays a crucial role in this paper:
Definition 2.4. Let X be a smooth projective variety. Let
![]() $f : \mathbb P^1 \to X$
be a rational curve that is not contracted to a point. We say f is free if the restricted tangent bundle
$f : \mathbb P^1 \to X$
be a rational curve that is not contracted to a point. We say f is free if the restricted tangent bundle
![]() $f^*T_X$
is nef. We say it is very free if
$f^*T_X$
is nef. We say it is very free if
![]() $f^*T_X$
is ample.
$f^*T_X$
is ample.
When f is free, the obstruction space
![]() $H^1(\mathbb P^1, N_f)$
vanishes where
$H^1(\mathbb P^1, N_f)$
vanishes where
![]() $N_f$
is the normal sheaf. In particular, the moduli stack
$N_f$
is the normal sheaf. In particular, the moduli stack
![]() $\mathcal M_{0,0}(X)$
is smooth at the point corresponding to f.
$\mathcal M_{0,0}(X)$
is smooth at the point corresponding to f.
If f is a free curve, then the deformations of f yield a dominant family of rational curves on X. Conversely, if we have a dominant family of rational curves then for a general point
![]() $x \in X$
every curve f that meets x is free. (See [Reference KollárKol96, II.3.5 Proposition].) By [Reference KollárKol96, II.3.13 Lemma], every free curve
$x \in X$
every curve f that meets x is free. (See [Reference KollárKol96, II.3.5 Proposition].) By [Reference KollárKol96, II.3.13 Lemma], every free curve
![]() $f: \mathbb {P}^{1} \to X$
must satisfy
$f: \mathbb {P}^{1} \to X$
must satisfy
![]() $\deg (f^{*}T_{X}) \geq 2$
.
$\deg (f^{*}T_{X}) \geq 2$
.
We also need the following birational invariant in the analysis of Fano threefolds:
Definition 2.5. Let X be a smooth projective variety and L be a big and nef
![]() $\mathbb Q$
-Cartier divisor on X. We define the Fujita invariant
$\mathbb Q$
-Cartier divisor on X. We define the Fujita invariant
![]() $a(X, L)$
to be
$a(X, L)$
to be
It follows from [Reference Boucksom, Demailly, Paun and PeternellBDPP13] that
![]() $a(X, L)$
is positive if and only if X is uniruled. When L is nef but not big, we formally set
$a(X, L)$
is positive if and only if X is uniruled. When L is nef but not big, we formally set
![]() $a(X, L) = +\infty $
.
$a(X, L) = +\infty $
.
When X is singular, we define the Fujita invariant
![]() $a(X, L)$
by taking a smooth resolution
$a(X, L)$
by taking a smooth resolution
![]() $\beta : \widetilde {X} \to X$
:
$\beta : \widetilde {X} \to X$
:
This is well defined due to the birational invariance of
![]() $a(X, L)$
(see [Reference Hassett, Tanimoto and TschinkelHTT15, Proposition 2.7]).
$a(X, L)$
(see [Reference Hassett, Tanimoto and TschinkelHTT15, Proposition 2.7]).
2.1 Notation
In this paper, we use Grothendieck’s notation for projective bundles, that is,
![]() $\mathbb P(V)$
parametrizes rank
$\mathbb P(V)$
parametrizes rank
![]() $1$
quotients of V.
$1$
quotients of V.
We will use the following notation when we discuss GW invariants. We will denote an object parametrized by
![]() $\overline {\mathcal {M}}_{g,m}(X,\beta )$
using the notation
$\overline {\mathcal {M}}_{g,m}(X,\beta )$
using the notation
![]() $f: (\widetilde {C}, \widetilde {q}_{1}, \ldots , \widetilde {q}_{m}) \to X$
, where
$f: (\widetilde {C}, \widetilde {q}_{1}, \ldots , \widetilde {q}_{m}) \to X$
, where
![]() $f: \widetilde {C} \to X$
is a stable map and the
$f: \widetilde {C} \to X$
is a stable map and the
![]() $\widetilde {q}_{i}$
are the marked points on
$\widetilde {q}_{i}$
are the marked points on
![]() $\widetilde {C}$
. We will also let
$\widetilde {C}$
. We will also let
![]() $(C,q_{1},\ldots ,q_{m}) \in \overline {\mathcal M}_{g,m}$
denote the stabilization of the prestable curve
$(C,q_{1},\ldots ,q_{m}) \in \overline {\mathcal M}_{g,m}$
denote the stabilization of the prestable curve
![]() $(\widetilde {C}, \widetilde {q}_{1}, \ldots , \widetilde {q}_{m})$
. Note that for every irreducible component
$(\widetilde {C}, \widetilde {q}_{1}, \ldots , \widetilde {q}_{m})$
. Note that for every irreducible component
![]() $C_{j}$
of C there is a unique irreducible component
$C_{j}$
of C there is a unique irreducible component
![]() $\widetilde {C}_{j} \subset \widetilde {C}$
that maps birationally to
$\widetilde {C}_{j} \subset \widetilde {C}$
that maps birationally to
![]() $C_{j}$
under the stabilization map. (When
$C_{j}$
under the stabilization map. (When
![]() $\widetilde {C}_{j}$
and
$\widetilde {C}_{j}$
and
![]() $C_{j}$
are isomorphic, we will often abuse notation and write
$C_{j}$
are isomorphic, we will often abuse notation and write
![]() $C_{j} \subset \widetilde {C}$
.) Since every marked point
$C_{j} \subset \widetilde {C}$
.) Since every marked point
![]() $q_{i}$
is contained in a unique irreducible component
$q_{i}$
is contained in a unique irreducible component
![]() $C_{j}$
, we can uniquely identify corresponding points
$C_{j}$
, we can uniquely identify corresponding points
![]() $q_{i} \in \widetilde {C}_{j} \subset \widetilde {C}$
(which may be either marked points or nodes in
$q_{i} \in \widetilde {C}_{j} \subset \widetilde {C}$
(which may be either marked points or nodes in
![]() $\widetilde {C}$
).
$\widetilde {C}$
).
3 Failure of asymptotic enumerativity
In this section, we describe two types of Fano varieties X not satisfying asymptotic enumerativity, giving counterexamples to [Reference Lian and PandharipandeLP23, Speculation 12].
3.1 Conical Fano manifolds
For this subsection, X will denote a Fano manifold of Picard rank
![]() $1$
and Fano index r and we say that a rational curve C on X is a line if it has anticanonical degree r (or equivalently, degree
$1$
and Fano index r and we say that a rational curve C on X is a line if it has anticanonical degree r (or equivalently, degree
![]() $1$
against an ample generator of the Picard group).
$1$
against an ample generator of the Picard group).
Definition 3.1. Let X be a Fano manifold with Picard rank
![]() $1$
and Fano index r. For any positive integer t, we say that X is t-general if there exists a family of free rational curves of anticanonical degree
$1$
and Fano index r. For any positive integer t, we say that X is t-general if there exists a family of free rational curves of anticanonical degree
![]() $tr$
on X.
$tr$
on X.
We say that X is conical if also there exists an irreducible divisor D in X containing a point p, the vertex, such that every point of D is contained in a line
![]() $\ell \subset D$
through p.
$\ell \subset D$
through p.
Example 3.2. Let
![]() $X\subset \mathbb {P}^{n}$
be a smooth hypersurface of degree
$X\subset \mathbb {P}^{n}$
be a smooth hypersurface of degree
![]() $d\le n$
with
$d\le n$
with
![]() $n\ge 4$
. Then, X has Picard rank 1 and Fano index
$n\ge 4$
. Then, X has Picard rank 1 and Fano index
![]() $n-d+1$
. If
$n-d+1$
. If
![]() $d\le n-1$
, then X is 1-general [Reference DebarreDeb15, Proposition 2.13], that is, covered by free lines. If
$d\le n-1$
, then X is 1-general [Reference DebarreDeb15, Proposition 2.13], that is, covered by free lines. If
![]() $d=n$
, then X is 2-general, that is, covered by free conics [Reference LewisLew85]; see also [Reference DebarreDeb15, Exercise 3.8]. More generally, a smooth Fano complete intersection X of type
$d=n$
, then X is 2-general, that is, covered by free conics [Reference LewisLew85]; see also [Reference DebarreDeb15, Exercise 3.8]. More generally, a smooth Fano complete intersection X of type
![]() $(d_1,\dots ,d_c)$
in
$(d_1,\dots ,d_c)$
in
![]() $\mathbb {P}^{n}$
is 1-general if the Fano index
$\mathbb {P}^{n}$
is 1-general if the Fano index
![]() $n-(d_1+\cdots +d_c)+1$
is at least 2 and 2-general if
$n-(d_1+\cdots +d_c)+1$
is at least 2 and 2-general if
![]() $n=d_1+\dots +d_c$
(see [Reference Coskun and RiedlCR19, Theorem 5.2]).
$n=d_1+\dots +d_c$
(see [Reference Coskun and RiedlCR19, Theorem 5.2]).
A smooth Fano complete intersection X as above is also conical if there exists a hyperplane section D of X that is itself a cone over a complete intersection of type
![]() $(d_1,\dots ,d_c)$
in
$(d_1,\dots ,d_c)$
in
![]() $\mathbb {P}^{n-2}$
. For example, a Fermat hypersurface X satisfies this property. Indeed, if a Fermat hypersurface is defined by the equation
$\mathbb {P}^{n-2}$
. For example, a Fermat hypersurface X satisfies this property. Indeed, if a Fermat hypersurface is defined by the equation
in
![]() $\mathbb P^n$
, then the hyperplane section D given by
$\mathbb P^n$
, then the hyperplane section D given by
![]() $x_0 -(-1)^{\frac {1}{d}}x_1 =0$
is a cone with the vertex
$x_0 -(-1)^{\frac {1}{d}}x_1 =0$
is a cone with the vertex
![]() $p = ((-1)^{\frac {1}{d}}:1:0:\cdots :0)$
.
$p = ((-1)^{\frac {1}{d}}:1:0:\cdots :0)$
.
Proposition 3.3. Let X be a conical Fano manifold of dimension N, Picard rank
![]() $1$
and Fano index r. Suppose that X is t-general for some positive integer t such that
$1$
and Fano index r. Suppose that X is t-general for some positive integer t such that
Then X fails to satisfy asymptotic enumerativity for all
![]() $g>0$
. If furthermore
$g>0$
. If furthermore
then X also fails to satisfy asymptotic enumerativity for
![]() $g=0$
.
$g=0$
.
Note that the hypothesis on t can only hold if
![]() $r\le \frac {N}{2}$
.
$r\le \frac {N}{2}$
.
Proof. Let
![]() $(C,q_1,\ldots ,q_m)\in \mathcal {M}_{g,m}$
be a general curve, and let
$(C,q_1,\ldots ,q_m)\in \mathcal {M}_{g,m}$
be a general curve, and let
![]() $p_1,\ldots ,p_m\in X$
be general points. Let
$p_1,\ldots ,p_m\in X$
be general points. Let
![]() $e,m$
be any integers for which
$e,m$
be any integers for which
For all m if
![]() $g> 0$
and m sufficiently large if
$g> 0$
and m sufficiently large if
![]() $ g=0$
, we have
$ g=0$
, we have
Let
![]() $(\widetilde {C},\widetilde {q}_1,\ldots ,\widetilde {q}_m)$
be the nodal curve depicted in Figure 1, obtained by attaching to C at each
$(\widetilde {C},\widetilde {q}_1,\ldots ,\widetilde {q}_m)$
be the nodal curve depicted in Figure 1, obtained by attaching to C at each
![]() $q_i$
a chain of two rational curves
$q_i$
a chain of two rational curves
![]() $R_i\cup S_i$
, where
$R_i\cup S_i$
, where
![]() $R_i$
intersects C at
$R_i$
intersects C at
![]() $q_i$
and
$q_i$
and
![]() $S_i$
at
$S_i$
at
![]() $z_i$
, and
$z_i$
, and
![]() $\widetilde {q}_i\in S_i$
is a smooth point.
$\widetilde {q}_i\in S_i$
is a smooth point.

Figure 1 The curve
![]() $\widetilde {C}=C\cup (R_1\cup S_1)\cdots \cup (R_{m}\cup S_m)$
.
$\widetilde {C}=C\cup (R_1\cup S_1)\cdots \cup (R_{m}\cup S_m)$
.
We define a stable map
![]() $f:\widetilde {C}\to X$
as follows:
$f:\widetilde {C}\to X$
as follows:
-
•
 $f|_{C}:C\to X$
is a constant map with image
$f|_{C}:C\to X$
is a constant map with image
 $p\in D$
.
$p\in D$
. -
•
 $f|_{S_i}:S_i\to X$
is a free curve of degree
$f|_{S_i}:S_i\to X$
is a free curve of degree
 $tr$
with
$tr$
with
 $f(\widetilde {q}_i)=p_i$
and
$f(\widetilde {q}_i)=p_i$
and
 $f(z_i)\in D$
: Such a map
$f(z_i)\in D$
: Such a map
 $f|_{S_i}$
exists because X is t-general and of Picard rank 1, hence D is ample.
$f|_{S_i}$
exists because X is t-general and of Picard rank 1, hence D is ample. -
•
 $f|_{R_i}:R_i\to X$
is an isomorphism onto a line in D with
$f|_{R_i}:R_i\to X$
is an isomorphism onto a line in D with
 $f(q_i)=p$
and
$f(q_i)=p$
and
 $f|_{R_i}(z_i)=f|_{S_i}(z_i)$
.
$f|_{R_i}(z_i)=f|_{S_i}(z_i)$
.
As defined above, f has degree
![]() $m(t+1)r\le er$
but can be modified to be a stable map of degree exactly
$m(t+1)r\le er$
but can be modified to be a stable map of degree exactly
![]() $er$
by replacing any
$er$
by replacing any
![]() $f|_{R_i}$
with a multiple cover of the appropriate degree.
$f|_{R_i}$
with a multiple cover of the appropriate degree.
Since f is a point in the boundary of
![]() $\overline {\mathcal {M}}_{g,m}(X,\beta )$
over a general point of
$\overline {\mathcal {M}}_{g,m}(X,\beta )$
over a general point of
![]() $\overline {\mathcal {M}}_{g,m}\times X^{\times m}$
,
$\overline {\mathcal {M}}_{g,m}\times X^{\times m}$
,
![]() $\text {GW}^{X,\text {fd}}_{g,\beta ,m}$
fails to be enumerative.
$\text {GW}^{X,\text {fd}}_{g,\beta ,m}$
fails to be enumerative.
Example 3.4. In particular, when X is a Fermat hypersurface X of degree d in
![]() $\mathbb {P}^{n}$
such that
$\mathbb {P}^{n}$
such that
![]() $n-1 \geq d> \frac {n+3}{2}$
, then asymptotic enumerativity fails in every genus.
$n-1 \geq d> \frac {n+3}{2}$
, then asymptotic enumerativity fails in every genus.
Example 3.5. Suppose X is a smooth quartic threefold with a conical hyperplane section D. Proposition 3.3 shows that X does not satisfy asymptotic enumerativity for any
![]() $g>0$
.
$g>0$
.
Example 3.6. Recall that in Remark 1.12 we discussed the relationship between Fujita invariants and the failure of asymptotic enumerativity. Proposition 3.3 shows one of the claims in Remark 1.12: The failure of asymptotic enumerativity cannot always be explained by the Fujita invariant. More precisely, suppose that X is a smooth hypersurface of degree d in
![]() $\mathbb {P}^{n}$
which admits a conical hyperplane section D. Furthermore, suppose the degree d satisfies
$\mathbb {P}^{n}$
which admits a conical hyperplane section D. Furthermore, suppose the degree d satisfies
The proof of Proposition 3.3 shows that we can violate asymptotic enumerativity using curves which connect through the conical hyperplane section D. However, we show that
![]() $a(D,-K_{X}) < a(X,-K_{X})$
. (This should be contrasted with Theorem 4.3 which guarantees that no such example exists amongst Fano threefolds.)
$a(D,-K_{X}) < a(X,-K_{X})$
. (This should be contrasted with Theorem 4.3 which guarantees that no such example exists amongst Fano threefolds.)
Note that D is a cone over a hypersurface Z of dimension
![]() $n-3$
and degree d in
$n-3$
and degree d in
![]() $\mathbb {P}^{n-2}$
. The variety
$\mathbb {P}^{n-2}$
. The variety
![]() $\widetilde {D} = \mathbb {P}_{Z}(\mathcal {O} \oplus \mathcal {O}(1))$
is a resolution of singularities of D. We let
$\widetilde {D} = \mathbb {P}_{Z}(\mathcal {O} \oplus \mathcal {O}(1))$
is a resolution of singularities of D. We let
![]() $\xi $
denote a divisor representing
$\xi $
denote a divisor representing
![]() $\mathcal {O}_{\widetilde {D}/Z}(1)$
and L denote the pullback of a hyperplane on Z. Then
$\mathcal {O}_{\widetilde {D}/Z}(1)$
and L denote the pullback of a hyperplane on Z. Then
The pseudo-effective cone of divisors on
![]() $K_{\widetilde {D}}$
is generated by L and by
$K_{\widetilde {D}}$
is generated by L and by
![]() $\xi - L$
. Consider divisors of the form
$\xi - L$
. Consider divisors of the form
![]() $K_{\widetilde {D}} + a\xi $
. The assumption
$K_{\widetilde {D}} + a\xi $
. The assumption
![]() $d < n-2$
implies that the smallest value of a for which this divisor lies in the pseudo-effective cone of
$d < n-2$
implies that the smallest value of a for which this divisor lies in the pseudo-effective cone of
![]() $\widetilde {D}$
is
$\widetilde {D}$
is
![]() $a = n-d$
. Since
$a = n-d$
. Since
![]() $-\phi ^{*}K_{X} = (n+1-d)\xi $
, we conclude that
$-\phi ^{*}K_{X} = (n+1-d)\xi $
, we conclude that
3.2 Projective bundles
Choose positive integers
![]() $n,r$
with
$n,r$
with
![]() $n>r+1$
, and choose an r-tuple
$n>r+1$
, and choose an r-tuple
![]() $(a_{1},\ldots ,a_{r})$
of nonnegative integers arranged in nondecreasing order. Set
$(a_{1},\ldots ,a_{r})$
of nonnegative integers arranged in nondecreasing order. Set
![]() $\mathcal {E} = \mathcal {O}_{\mathbb {P}^{n-r}} \oplus \mathcal {O}_{\mathbb {P}^{n-r}}(a_{1}) \oplus \ldots \mathcal {O}_{\mathbb {P}^{n-r}}(a_{r})$
. (Note that the first summand of
$\mathcal {E} = \mathcal {O}_{\mathbb {P}^{n-r}} \oplus \mathcal {O}_{\mathbb {P}^{n-r}}(a_{1}) \oplus \ldots \mathcal {O}_{\mathbb {P}^{n-r}}(a_{r})$
. (Note that the first summand of
![]() $\mathcal {E}$
is trivial.)
$\mathcal {E}$
is trivial.)
Let
![]() $X = \mathbb {P}_{\mathbb {P}^{n-r}}(\mathcal {E})$
equipped with the projective bundle morphism
$X = \mathbb {P}_{\mathbb {P}^{n-r}}(\mathcal {E})$
equipped with the projective bundle morphism
![]() $\pi : X \to \mathbb {P}^{n-r}$
. We let Z denote the ‘most rigid’ section of
$\pi : X \to \mathbb {P}^{n-r}$
. We let Z denote the ‘most rigid’ section of
![]() $\pi $
corresponding to the surjection
$\pi $
corresponding to the surjection
![]() $\mathcal {E} \to \mathcal {O}$
onto the first factor. If we let H denote the
$\mathcal {E} \to \mathcal {O}$
onto the first factor. If we let H denote the
![]() $\pi $
-pullback of the hyperplane class from
$\pi $
-pullback of the hyperplane class from
![]() $\mathbb {P}^{n-r}$
and
$\mathbb {P}^{n-r}$
and
![]() $\xi $
denote the class of the relative
$\xi $
denote the class of the relative
![]() $\mathcal {O}(1)$
, then
$\mathcal {O}(1)$
, then
Dually, if we let
![]() $\ell $
denote the class of a line in a fiber of
$\ell $
denote the class of a line in a fiber of
![]() $\pi $
and C denote the class of a line in Z, then
$\pi $
and C denote the class of a line in Z, then
The anticanonical divisor is
![]() $-K_{X} = (r+1)\xi + (n-r+1 - \sum _{i=1}^{r} a_{i})H$
. In particular, X will be Fano if and only if
$-K_{X} = (r+1)\xi + (n-r+1 - \sum _{i=1}^{r} a_{i})H$
. In particular, X will be Fano if and only if
![]() $\sum _{i=1}^{r} a_{i} \leq n-r$
.
$\sum _{i=1}^{r} a_{i} \leq n-r$
.
In this section, we show that fixed-domain GW invariants
![]() $\text {GW}^{X,\text {fd}}_{g,\beta ,m}$
fail to be enumerative for many Fano varieties X given by the construction above.
$\text {GW}^{X,\text {fd}}_{g,\beta ,m}$
fail to be enumerative for many Fano varieties X given by the construction above.
Proposition 3.7. Let
![]() $X = {\mathbb P}_{\mathbb {P}^{n-r}}(\mathcal {E})$
be a Fano projective bundle with
$X = {\mathbb P}_{\mathbb {P}^{n-r}}(\mathcal {E})$
be a Fano projective bundle with
![]() $n> r+1$
and with notation as above. Suppose that
$n> r+1$
and with notation as above. Suppose that
 $$ \begin{align*} \sum_{i=1}^{r} a_i \geq 2. \end{align*} $$
$$ \begin{align*} \sum_{i=1}^{r} a_i \geq 2. \end{align*} $$
Let
![]() $g\ge 0$
be any genus.
$g\ge 0$
be any genus.
Then, there exist fixed-domain triples
![]() $(g,\delta ,m)$
with m arbitrarily large for which there exists a positive-dimensional family of genus g reducible curves of degree
$(g,\delta ,m)$
with m arbitrarily large for which there exists a positive-dimensional family of genus g reducible curves of degree
![]() $\delta $
with fixed moduli through m general points. In particular, asymptotic enumerativity fails for X in every genus.
$\delta $
with fixed moduli through m general points. In particular, asymptotic enumerativity fails for X in every genus.
The construction is simple: Through m general points, we can find a comb whose handle is a genus g curve which lies in Z and whose teeth are rational curves in the fibers of
![]() $\pi $
. Such combs will have higher than expected dimension.
$\pi $
. Such combs will have higher than expected dimension.
Proof. For any
![]() $g,m\ge 0$
with
$g,m\ge 0$
with
![]() $3g-3+m\ge 0$
, define
$3g-3+m\ge 0$
, define
![]() $\delta = n(m+g-1)$
so that
$\delta = n(m+g-1)$
so that
![]() $(g,\delta ,m)$
is a fixed-domain triple. Fix general points
$(g,\delta ,m)$
is a fixed-domain triple. Fix general points
![]() $p_{1},\ldots ,p_{m} \in X$
, and let
$p_{1},\ldots ,p_{m} \in X$
, and let
![]() $(C,q_1,\ldots ,q_m)\in {\mathcal M}_{g,m}$
be a general curve. Let
$(C,q_1,\ldots ,q_m)\in {\mathcal M}_{g,m}$
be a general curve. Let
![]() $(\widetilde {C},\widetilde {q}_1,\ldots ,\widetilde {q}_m)$
be the nodal curve obtained by attaching to C at
$(\widetilde {C},\widetilde {q}_1,\ldots ,\widetilde {q}_m)$
be the nodal curve obtained by attaching to C at
![]() $q_i$
a single rational tail
$q_i$
a single rational tail
![]() $T_i$
with smooth marked point
$T_i$
with smooth marked point
![]() $\widetilde {q}_i$
; see Figure 2.
$\widetilde {q}_i$
; see Figure 2.

Figure 2 The curve
![]() $\widetilde {C}=C\cup T_1\cup \cdots \cup T_{m}$
.
$\widetilde {C}=C\cup T_1\cup \cdots \cup T_{m}$
.
Consider the set of morphisms
![]() $f:\widetilde {C} \to X$
of the following form.
$f:\widetilde {C} \to X$
of the following form.
-
• each
 $T_{i}$
is mapped to a rational curve in the fiber of
$T_{i}$
is mapped to a rational curve in the fiber of
 $\pi $
such that
$\pi $
such that
 $f(\widetilde {q}_i)=p_{i}$
and
$f(\widetilde {q}_i)=p_{i}$
and
 $f(q_i)\in Z$
;
$f(q_i)\in Z$
; -
• C is mapped to Z, necessarily containing the points
 $f|_{T_i}(q_i)$
.
$f|_{T_i}(q_i)$
.
Write
![]() $\gamma =n - r + 1 - \sum _{i=1}^{r}a_{i}$
. Let
$\gamma =n - r + 1 - \sum _{i=1}^{r}a_{i}$
. Let
![]() $\delta _0$
be the degree of
$\delta _0$
be the degree of
![]() $f|_{C}$
in Z, and let
$f|_{C}$
in Z, and let
![]() $m'$
denote the intersection
$m'$
denote the intersection
![]() $\xi \cdot \left ( \sum _{j=1}^{m} f(T_{j}) \right )$
recording the total degree of the teeth
$\xi \cdot \left ( \sum _{j=1}^{m} f(T_{j}) \right )$
recording the total degree of the teeth
![]() $T_1,\ldots ,T_m$
with respect to the relative hyperplane class. The condition
$T_1,\ldots ,T_m$
with respect to the relative hyperplane class. The condition
![]() $\delta = n(m+g-1)$
implies that these constants must satisfy
$\delta = n(m+g-1)$
implies that these constants must satisfy
Fix a sufficiently large positive integer k, and set
![]() $m=k\gamma -g+1$
. We may choose our curve
$m=k\gamma -g+1$
. We may choose our curve
![]() $\widetilde {C}$
so that
$\widetilde {C}$
so that
![]() $m' = (k+1) \gamma \ge m$
. We find that
$m' = (k+1) \gamma \ge m$
. We find that
Since we are assuming that
![]() $n>r+1$
, the degree
$n>r+1$
, the degree
![]() $\delta _{0}$
is positive for k sufficiently large.
$\delta _{0}$
is positive for k sufficiently large.
Next, consider the space parametrizing morphisms
![]() $f_0:C\to Z\cong \mathbb {P}^{n-r}$
of degree
$f_0:C\to Z\cong \mathbb {P}^{n-r}$
of degree
![]() $\delta _0$
for which
$\delta _0$
for which
![]() $f_0(q_i)=f|_{T_i}(q_i)$
. This space is nonempty of dimension
$f_0(q_i)=f|_{T_i}(q_i)$
. This space is nonempty of dimension
so long as this number is nonnegative, by [Reference LarsonLar16, Corollary 1.3] and the Brill–Noether theorem. Substituting our earlier value for
![]() $\delta _{0}$
, this number is equal to
$\delta _{0}$
, this number is equal to
 $$ \begin{align*} (k(n-r-1)-(r+1))&(n-r+1) + (n-r) - (m+g)(n-r) \\ =k[&(n-r-1)(n-r+1)-\gamma(n-r)]+B, \end{align*} $$
$$ \begin{align*} (k(n-r-1)-(r+1))&(n-r+1) + (n-r) - (m+g)(n-r) \\ =k[&(n-r-1)(n-r+1)-\gamma(n-r)]+B, \end{align*} $$
where B only depends on
![]() $n,r,g$
. Thus, the dimension of this space of maps is positive as long as k is sufficiently large and
$n,r,g$
. Thus, the dimension of this space of maps is positive as long as k is sufficiently large and
 $$ \begin{align*} n-r+1-\sum_{i=1}^r a_i = \gamma<\frac{(n-r-1)(n-r+1)}{n-r}, \end{align*} $$
$$ \begin{align*} n-r+1-\sum_{i=1}^r a_i = \gamma<\frac{(n-r-1)(n-r+1)}{n-r}, \end{align*} $$
which happens whenever
![]() $\sum _{i=1}^r a_i \ge 2$
.
$\sum _{i=1}^r a_i \ge 2$
.
Thus, there is a positive-dimensional family of such
![]() $f:\widetilde {C}\to X$
with the needed properties, completing the proof.
$f:\widetilde {C}\to X$
with the needed properties, completing the proof.
Remark 3.8. The bound
![]() $\sum _{i=1}^{r}a_i\ge 2$
is sharp. When
$\sum _{i=1}^{r}a_i\ge 2$
is sharp. When
![]() $r=1$
and
$r=1$
and
![]() $a_1=1$
,
$a_1=1$
,
![]() $X=\mathbb {P}_{\mathbb {P}^{n-1}}({\mathcal O}\oplus {\mathcal O}(1))$
is isomorphic to the blowup of
$X=\mathbb {P}_{\mathbb {P}^{n-1}}({\mathcal O}\oplus {\mathcal O}(1))$
is isomorphic to the blowup of
![]() $\mathbb {P}^n$
at one point, for which asymptotic enumerativity holds by [Reference Cela and LianCL23, Theorem 23].
$\mathbb {P}^n$
at one point, for which asymptotic enumerativity holds by [Reference Cela and LianCL23, Theorem 23].
Example 3.9. The unique example of a Fano projective bundle of dimension
![]() $3$
that satisfies the conditions of Proposition 3.7 is
$3$
that satisfies the conditions of Proposition 3.7 is
![]() $X=\mathbb {P}_{\mathbb {P}^{2}}({\mathcal O}\oplus {\mathcal O}(2))$
.
$X=\mathbb {P}_{\mathbb {P}^{2}}({\mathcal O}\oplus {\mathcal O}(2))$
.
4 Fano threefolds
In this section, we study enumerativity of fixed-domain GW invariants for Fano threefolds. Our intuition is shaped by [Reference Beheshti, Lehmann, Riedl and TanimotoBLRT22, Theorem 1.2] which shows that if X carries a nondominant family of rational curves then these curves must sweep out a surface
![]() $Y \subset X$
satisfying one of the following conditions:
$Y \subset X$
satisfying one of the following conditions:
-
1. Y is swept out by anticanonical lines, or
-
2. Y is an exceptional divisor for a birational contraction on X.
In other words, divisors Y as above account for all ‘unexpected’ families of rational curves. We prove that the failure of asymptotic enumerativity for a Fano threefold is also explained by the presence of such divisors Y.
We will frequently use Mori’s classification of the exceptional divisors E on smooth Fano threefolds into five types ([Reference MoriMor82]):
-
• E1: an exceptional divisor for a blowup along a smooth curve
-
• E2: an exceptional divisor for a blowup at a smooth point
-
• E3: the polarized surface
 $(E, -K_X|_E)$
is isomorphic to
$(E, -K_X|_E)$
is isomorphic to
 $(Q, \mathcal O(1, 1))$
where Q is a smooth quadric surface
$(Q, \mathcal O(1, 1))$
where Q is a smooth quadric surface -
• E4: the polarized surface
 $(E, -K_X|_E)$
is isomorphic to
$(E, -K_X|_E)$
is isomorphic to
 $(Q, \mathcal O(1))$
where Q is a quadric cone in
$(Q, \mathcal O(1))$
where Q is a quadric cone in
 $\mathbb {P}^{3}$
$\mathbb {P}^{3}$
-
• E5: the polarized surface
 $(E, -K_X|_E)$
is isomorphic to
$(E, -K_X|_E)$
is isomorphic to
 $(\mathbb P^2, \mathcal O(1))$
.
$(\mathbb P^2, \mathcal O(1))$
.
In this section, we will say that a rational curve
![]() $C \subset X$
is a line (respectively, conic, cubic) if C has anticanonical degree
$C \subset X$
is a line (respectively, conic, cubic) if C has anticanonical degree
![]() $1$
(resp.
$1$
(resp.
![]() $2$
,
$2$
,
![]() $3$
). Note that this differs from the conventions for complete intersections in
$3$
). Note that this differs from the conventions for complete intersections in
![]() $\mathbb {P}^{n}$
used in Section 3.1 and Section 5. We first need the following result of [Reference Lian and PandharipandeLP23] which applies to stable maps with irreducible domain:
$\mathbb {P}^{n}$
used in Section 3.1 and Section 5. We first need the following result of [Reference Lian and PandharipandeLP23] which applies to stable maps with irreducible domain:
Lemma 4.1 ([Reference Lian and PandharipandeLP23] Proposition 13 and Proposition 14)
Let X be a smooth projective variety, and fix
![]() $m \geq g+1$
. Suppose that
$m \geq g+1$
. Suppose that
![]() $s: ({C},{q}_{1},\ldots ,{q}_{m}) \to X$
is an element of
$s: ({C},{q}_{1},\ldots ,{q}_{m}) \to X$
is an element of
![]() $\mathcal {M}_{g,m}(X,\beta )$
that lies over a general point
$\mathcal {M}_{g,m}(X,\beta )$
that lies over a general point
![]() $((C,q_{1},\ldots ,q_{m}),p_{1},\ldots ,p_{m}) \in \mathcal {M}_{g,m} \times X^{\times m}$
. Then the local dimension of
$((C,q_{1},\ldots ,q_{m}),p_{1},\ldots ,p_{m}) \in \mathcal {M}_{g,m} \times X^{\times m}$
. Then the local dimension of
![]() $\mathcal {M}_{g,m}(X,\beta )$
at s has the expected value
$\mathcal {M}_{g,m}(X,\beta )$
at s has the expected value
We also need the following estimate for stable maps with irreducible domain:
Lemma 4.2. Let X be a smooth projective variety, and fix
![]() $m \geq 1$
. Suppose that
$m \geq 1$
. Suppose that
![]() $s: ({C},{q}_{1},\ldots ,{q}_{m}) \to X$
is an element of
$s: ({C},{q}_{1},\ldots ,{q}_{m}) \to X$
is an element of
![]() $\mathcal {M}_{g,m}(X,\beta )$
that lies over a general point
$\mathcal {M}_{g,m}(X,\beta )$
that lies over a general point
![]() $(C,p_1)\in {\mathcal M}_g\times X$
, where
$(C,p_1)\in {\mathcal M}_g\times X$
, where
![]() $p_{1}$
denotes the image of
$p_{1}$
denotes the image of
![]() ${q}_{1}$
under the first evaluation map
${q}_{1}$
under the first evaluation map
![]() $ev_{1}: \mathcal {M}_{g,m}(X,\beta )\to X$
. Then the local dimension of
$ev_{1}: \mathcal {M}_{g,m}(X,\beta )\to X$
. Then the local dimension of
![]() $\mathcal {M}_{g,m}(X,\beta )$
at s satisfies
$\mathcal {M}_{g,m}(X,\beta )$
at s satisfies
Proof. It follows from deformation theory that we have
Since
![]() $s : {C} \to X$
deforms to cover X, we conclude that
$s : {C} \to X$
deforms to cover X, we conclude that
![]() $N_{s/X}$
is generically globally generated. (See, e.g., [Reference Lehmann and TanimotoLT22, Proposition 3.3]) It follows from [Reference Lehmann, Riedl and TanimotoLRT23, Lemma 2.8] that we have
$N_{s/X}$
is generically globally generated. (See, e.g., [Reference Lehmann and TanimotoLT22, Proposition 3.3]) It follows from [Reference Lehmann, Riedl and TanimotoLRT23, Lemma 2.8] that we have
Thus, our assertion follows.
Our main statement for Fano threefolds relates the enumerativity of fixed-domain GW invariants with the existence of subvarieties
![]() $Y \subset X$
with large Fujita invariant. Recall that for an m-pointed genus g curve of anticanonical degree d on a Fano threefold the fixed-domain triple condition is
$Y \subset X$
with large Fujita invariant. Recall that for an m-pointed genus g curve of anticanonical degree d on a Fano threefold the fixed-domain triple condition is
![]() $d = 3m+3g-3$
.
$d = 3m+3g-3$
.
Theorem 4.3. Let X be a smooth Fano threefold. Let
![]() $g\ge 0$
be a fixed genus. Suppose that there exist arbitrarily large
$g\ge 0$
be a fixed genus. Suppose that there exist arbitrarily large
![]() $m\ge 0$
with the following property. There exists
$m\ge 0$
with the following property. There exists
![]() $\beta \in N_{1}(X)_{\mathbb {Z}}$
of anticanonical degree
$\beta \in N_{1}(X)_{\mathbb {Z}}$
of anticanonical degree
![]() $d\le 3m+3g-3$
and an irreducible component
$d\le 3m+3g-3$
and an irreducible component
![]() $M_m \subset \overline {{\mathcal M}}_{g,m}(X,\beta )$
such that
$M_m \subset \overline {{\mathcal M}}_{g,m}(X,\beta )$
such that
![]() $M_m$
is contained in the boundary of
$M_m$
is contained in the boundary of
![]() $\overline {{\mathcal M}}_{g,m}(X,\beta )$
and such that the map
$\overline {{\mathcal M}}_{g,m}(X,\beta )$
and such that the map
is dominant.
Then, for any m sufficiently large, a general point
![]() $f:(\widetilde {C},\widetilde {q}_1,\ldots ,\widetilde {q}_m)\to X$
of the fiber
$f:(\widetilde {C},\widetilde {q}_1,\ldots ,\widetilde {q}_m)\to X$
of the fiber
![]() $M_{m, 0}\subset M_m$
over a general point
$M_{m, 0}\subset M_m$
over a general point
![]() $(C,q_1,\ldots ,q_m)\in {\mathcal M}_{g,m}$
has one of the following three properties.
$(C,q_1,\ldots ,q_m)\in {\mathcal M}_{g,m}$
has one of the following three properties.
-
(i) f contracts the central genus g component
 $C\subset \widetilde {C}$
to a point
$C\subset \widetilde {C}$
to a point
 $p\in X$
(independent of the
$p\in X$
(independent of the
 $q_i$
), through which there exists a one-parameter *family of* lines in X,
$q_i$
), through which there exists a one-parameter *family of* lines in X, -
(ii) the central genus g component
 $C\subset \widetilde {C}$
sweeps out a curve
$C\subset \widetilde {C}$
sweeps out a curve
 $Z\subset X$
(independent of the
$Z\subset X$
(independent of the
 $q_i$
) which is contained in an E5 divisor
$q_i$
) which is contained in an E5 divisor
 $Y\subset X$
, or
$Y\subset X$
, or -
(iii) the central genus g component
 $C\subset \widetilde {C}$
sweeps out a surface
$C\subset \widetilde {C}$
sweeps out a surface
 $Z \subset X$
with the property that
$Z \subset X$
with the property that
 $a(Z,-K_{X}|_{Z}) \ge 2$
.
$a(Z,-K_{X}|_{Z}) \ge 2$
.
[Reference Lehmann, Tanimoto and TschinkelLTT18, Proposition 4.1] shows that any surface
![]() $Z \subset X$
swept out by lines satisfies
$Z \subset X$
swept out by lines satisfies
![]() $a(Z,-K_{X}|_{Z}) \geq 2$
. Thus, in case (i) the surface Z swept out by the one-parameter lines through p will still have Fujita invariant at least 2. In case (ii), the E5 divisor Y has Fujita invariant 3. Therefore, X must contain a divisor of Fujita invariant at least 2 in all three cases.
$a(Z,-K_{X}|_{Z}) \geq 2$
. Thus, in case (i) the surface Z swept out by the one-parameter lines through p will still have Fujita invariant at least 2. In case (ii), the E5 divisor Y has Fujita invariant 3. Therefore, X must contain a divisor of Fujita invariant at least 2 in all three cases.
Proof. Suppose that
![]() $f:(\widetilde {C},\widetilde {q}_1,\ldots ,\widetilde {q}_m)\to X$
is a general stable map parametrized by
$f:(\widetilde {C},\widetilde {q}_1,\ldots ,\widetilde {q}_m)\to X$
is a general stable map parametrized by
![]() $M_m$
over a general point of
$M_m$
over a general point of
![]() $\overline {{\mathcal M}}_{g,m}\times X^{\times m}$
. Then the domain of f is the union of an irreducible genus g curve C with b genus
$\overline {{\mathcal M}}_{g,m}\times X^{\times m}$
. Then the domain of f is the union of an irreducible genus g curve C with b genus
![]() $0$
trees
$0$
trees
![]() $T_{1},\ldots ,T_{b}$
. After relabeling, we may suppose that if
$T_{1},\ldots ,T_{b}$
. After relabeling, we may suppose that if
![]() $T_i$
contains any marked point then it contains
$T_i$
contains any marked point then it contains
![]() $\widetilde {q}_i$
, and it meets C at
$\widetilde {q}_i$
, and it meets C at
![]() $q_i$
. We fix the moduli of the stabilized curve
$q_i$
. We fix the moduli of the stabilized curve
![]() $(C,q_1,\ldots ,q_m)$
throughout the proof and assume that
$(C,q_1,\ldots ,q_m)$
throughout the proof and assume that
![]() $\phi |_{M_m}$
remains dominant upon pullback over
$\phi |_{M_m}$
remains dominant upon pullback over
![]() $[(C,q_1,\ldots ,q_m)]\in {\mathcal M}_{g,m}$
for arbitrarily large m. That is, we assume that
$[(C,q_1,\ldots ,q_m)]\in {\mathcal M}_{g,m}$
for arbitrarily large m. That is, we assume that
![]() $M_{m, 0}$
dominates
$M_{m, 0}$
dominates
![]() $X^{\times m}$
.
$X^{\times m}$
.
We first make a series of reductions to constrain the topology of f. At the cost of decreasing d (preserving the inequality
![]() $d\le 3m+3g-3$
), we may assume that the tree
$d\le 3m+3g-3$
), we may assume that the tree
![]() $T_i$
contains the marked point
$T_i$
contains the marked point
![]() $\widetilde {q}_i$
by deleting all trees
$\widetilde {q}_i$
by deleting all trees
![]() $T_i$
that do not contain a marked point. We may furthermore assume that
$T_i$
that do not contain a marked point. We may furthermore assume that
![]() $T_i$
is a chain of rational curves with
$T_i$
is a chain of rational curves with
![]() $\widetilde {q}_i$
on the component furthest away from C, by successively deleting leaves on
$\widetilde {q}_i$
on the component furthest away from C, by successively deleting leaves on
![]() $T_i$
not containing
$T_i$
not containing
![]() $q_i$
, also at the cost of decreasing d.
$q_i$
, also at the cost of decreasing d.
Now, suppose that
![]() $T_i$
has anticanonical degree at least 4. Then, deleting
$T_i$
has anticanonical degree at least 4. Then, deleting
![]() $T_i$
and the points
$T_i$
and the points
![]() $p_i\in X$
and
$p_i\in X$
and
![]() $q_i\in C$
decreases d by at least 4 and m by 1, so still have
$q_i\in C$
decreases d by at least 4 and m by 1, so still have
![]() $d\le 3m+3g-3$
. On the other hand, this operation can be performed at most
$d\le 3m+3g-3$
. On the other hand, this operation can be performed at most
![]() $\frac {d}{4}\le \frac {3}{4}m+O(1)$
times, where here and in the rest of the proof the implicit constant
$\frac {d}{4}\le \frac {3}{4}m+O(1)$
times, where here and in the rest of the proof the implicit constant
![]() $O(1)$
is allowed to depend on
$O(1)$
is allowed to depend on
![]() $g,X$
but not on m. In particular, we still have
$g,X$
but not on m. In particular, we still have
![]() $m\to \infty $
after this reduction. (We may also relabel the chains
$m\to \infty $
after this reduction. (We may also relabel the chains
![]() $T_i$
with the indices
$T_i$
with the indices
![]() $i=1,2,\ldots ,b$
after deleting some indices i.)
$i=1,2,\ldots ,b$
after deleting some indices i.)
If any components are deleted in the process described above, then we have
![]() $d<3m+3g-3$
. If the resulting curve
$d<3m+3g-3$
. If the resulting curve
![]() $\widetilde {C}$
is irreducible (that is,
$\widetilde {C}$
is irreducible (that is,
![]() $b=0$
) and m is sufficiently large, then by Lemma 4.1, the map
$b=0$
) and m is sufficiently large, then by Lemma 4.1, the map
![]() $\phi |_{M_m}$
cannot be dominant. Thus, we may assume that
$\phi |_{M_m}$
cannot be dominant. Thus, we may assume that
![]() $b>0$
.
$b>0$
.
Because the image of each chain
![]() $T_{i}$
contains a general point of X, we have
$T_{i}$
contains a general point of X, we have
![]() $\deg (T_{i}) \geq 2$
for each
$\deg (T_{i}) \geq 2$
for each
![]() $i \leq b$
. Indeed, the tree
$i \leq b$
. Indeed, the tree
![]() $T_i$
must contain a free curve of class
$T_i$
must contain a free curve of class
![]() $\beta _i$
, that is, we have a dominant map
$\beta _i$
, that is, we have a dominant map
![]() $\text {ev}:M_{0,1}(X,\beta _i)\to X$
. Lemma 4.1 shows that the anticanonical degree of
$\text {ev}:M_{0,1}(X,\beta _i)\to X$
. Lemma 4.1 shows that the anticanonical degree of
![]() $\beta _i$
must be at least 2. Thus, we may assume that
$\beta _i$
must be at least 2. Thus, we may assume that
![]() $\deg (T_i)\in \{2,3\}$
whenever
$\deg (T_i)\in \{2,3\}$
whenever
![]() $T_i$
is nonempty.
$T_i$
is nonempty.
If
![]() $\deg (T_{i}) = 2$
, then the image of
$\deg (T_{i}) = 2$
, then the image of
![]() $T_{i}$
is an irreducible conic through a general point. Amongst the set of chains
$T_{i}$
is an irreducible conic through a general point. Amongst the set of chains
![]() $T_{1},\ldots ,T_{b}$
, we let
$T_{1},\ldots ,T_{b}$
, we let
![]() $T_{1},\ldots ,T_{c}$
denote the trees which have anticanonical degree
$T_{1},\ldots ,T_{c}$
denote the trees which have anticanonical degree
![]() $2$
. The stability of f requires that such
$2$
. The stability of f requires that such
![]() $T_i$
are irreducible.
$T_i$
are irreducible.
If
![]() $\deg (T_{i}) = 3$
, then the image of
$\deg (T_{i}) = 3$
, then the image of
![]() $T_{i}$
with
$T_{i}$
with
![]() $i \leq b$
is either the union of a conic with a line or it is an irreducible cubic. Let
$i \leq b$
is either the union of a conic with a line or it is an irreducible cubic. Let
![]() $T_{c+1},\ldots ,T_{c+s}$
denote the chains which have anticanonical degree
$T_{c+1},\ldots ,T_{c+s}$
denote the chains which have anticanonical degree
![]() $3$
and contain a unique free component of degree 3. Again, the stability of f requires that such
$3$
and contain a unique free component of degree 3. Again, the stability of f requires that such
![]() $T_i$
are irreducible. Let
$T_i$
are irreducible. Let
![]() $T_{c+s+1},\ldots ,T_{b}$
denote the remaining trees which have anticanonical degree
$T_{c+s+1},\ldots ,T_{b}$
denote the remaining trees which have anticanonical degree
![]() $3$
and therefore contain both a line and a free conic. Write
$3$
and therefore contain both a line and a free conic. Write
![]() $s'=b-c-s$
. Then, by the stability of f and the assumption that
$s'=b-c-s$
. Then, by the stability of f and the assumption that
![]() $T_i$
is a chain, we must have
$T_i$
is a chain, we must have
![]() $T_i=L_i\cup C_i$
, where the line
$T_i=L_i\cup C_i$
, where the line
![]() $L_i$
appears between C and the free conic
$L_i$
appears between C and the free conic
![]() $C_i$
, which contains
$C_i$
, which contains
![]() $\widetilde {q}_i$
.
$\widetilde {q}_i$
.
The topology of
![]() $\widetilde {C}$
is depicted in Figure 3. We write
$\widetilde {C}$
is depicted in Figure 3. We write
![]() $d_0=d-2c-3s-3s'$
for the anticanonical degree of C and
$d_0=d-2c-3s-3s'$
for the anticanonical degree of C and
![]() $s_+=s+s'$
.
$s_+=s+s'$
.

Figure 3 The curve
![]() $\widetilde {C}=C\cup T_1\cdots \cup T_{b}$
.
$\widetilde {C}=C\cup T_1\cdots \cup T_{b}$
.
As we vary the points
![]() $p_1,\ldots ,p_m\in X$
in moduli, the corresponding maps
$p_1,\ldots ,p_m\in X$
in moduli, the corresponding maps
![]() $f:\widetilde {C}\to X$
will also deform. Let
$f:\widetilde {C}\to X$
will also deform. Let
![]() $Z\subset X$
be the subvariety of X swept out by C. We analyze the maps that appear depending on the dimension of Z, and show that, in order for such stable maps f through general points
$Z\subset X$
be the subvariety of X swept out by C. We analyze the maps that appear depending on the dimension of Z, and show that, in order for such stable maps f through general points
![]() $p_1,\ldots ,p_m$
to exist with m arbitrarily large, the stable map f must be of one of the three possible forms in the statement of the Theorem.
$p_1,\ldots ,p_m$
to exist with m arbitrarily large, the stable map f must be of one of the three possible forms in the statement of the Theorem.
Case 1:
![]() $\dim (Z)=0$
.
$\dim (Z)=0$
.
In this case, f contracts C to a point
![]() $p\in X$
. Neither a family of free conics nor cubics through a general point of X may pass through a fixed point
$p\in X$
. Neither a family of free conics nor cubics through a general point of X may pass through a fixed point
![]() $p\in X$
because passing through p imposes the expected number of conditions on any family of free curves. So we have
$p\in X$
because passing through p imposes the expected number of conditions on any family of free curves. So we have
![]() $c=s=0$
and
$c=s=0$
and
![]() $s'>0$
. We have
$s'>0$
. We have
![]() $T_1=L_1\cup C_1$
, where
$T_1=L_1\cup C_1$
, where
![]() $L_1\ni p$
is a line and
$L_1\ni p$
is a line and
![]() $C_1$
is a free conic. If there is no positive-dimensional family of lines through p, then there are only finitely many options for
$C_1$
is a free conic. If there is no positive-dimensional family of lines through p, then there are only finitely many options for
![]() $L_{1}$
. On the other hand, a general member of a family of free conics will avoid any fixed codimension
$L_{1}$
. On the other hand, a general member of a family of free conics will avoid any fixed codimension
![]() $2$
locus in X. Thus, a free conic
$2$
locus in X. Thus, a free conic
![]() $C_1$
through a general point cannot meet any of the finitely many lines through p, a contradiction. Thus, (i) must hold.
$C_1$
through a general point cannot meet any of the finitely many lines through p, a contradiction. Thus, (i) must hold.
Case 2:
![]() $Z=X$
.
$Z=X$
.
Because C sweeps out all of X, by Lemma 4.2 the space of deformations of
![]() $f|_{C}$
that preserve the pointed moduli of C has dimension at most
$f|_{C}$
that preserve the pointed moduli of C has dimension at most
![]() $d_0+O(1)$
. We now estimate the dimension of the image of
$d_0+O(1)$
. We now estimate the dimension of the image of
![]() $M_{m, 0}$
under
$M_{m, 0}$
under
![]() $\phi $
. First, observe that, given a fixed choice of
$\phi $
. First, observe that, given a fixed choice of
![]() $f|_C$
, we have:
$f|_C$
, we have:
-
• One parameter for the choice of a point
 $p_i$
on a free conic through
$p_i$
on a free conic through
 $f(q_i)$
, and
$f(q_i)$
, and -
• Two parameters for the choice of a point
 $p_i$
on a free cubic through
$p_i$
on a free cubic through
 $f(q_i)$
.
$f(q_i)$
.
that is, if the restriction of f to C is specified, then we get one (resp. two) additional degrees of freedom for the position of
![]() $f(\widetilde {q}_i)=p_i$
if
$f(\widetilde {q}_i)=p_i$
if
![]() $T_i\ni \widetilde {q}_i$
is a free conic (resp. free cubic).
$T_i\ni \widetilde {q}_i$
is a free conic (resp. free cubic).
Suppose instead that
![]() $T_i$
is a chain
$T_i$
is a chain
![]() $L_i\cup C_i$
. We may have a full three-parameter family of
$L_i\cup C_i$
. We may have a full three-parameter family of
![]() $p_i$
arising from choices of such
$p_i$
arising from choices of such
![]() $T_i$
. However, returning to our original setup, note that the lines
$T_i$
. However, returning to our original setup, note that the lines
![]() $L_{i}$
on X sweep out a finite union of divisors
$L_{i}$
on X sweep out a finite union of divisors
![]() $\{E_{j}\}$
. Since by assumption the deformations of C in the family
$\{E_{j}\}$
. Since by assumption the deformations of C in the family
![]() $M_{m,0}$
dominate X, the same is true if we consider the larger sublocus of
$M_{m,0}$
dominate X, the same is true if we consider the larger sublocus of
![]() $M_{m}$
where we fix C but allow the points
$M_{m}$
where we fix C but allow the points
![]() $(q_{1},\ldots ,q_{m})$
to vary in moduli on C. In this larger family, we see that forcing
$(q_{1},\ldots ,q_{m})$
to vary in moduli on C. In this larger family, we see that forcing
![]() $q_{i}$
to map to one of the divisors
$q_{i}$
to map to one of the divisors
![]() $E_{j}$
imposes one condition on the family of maps
$E_{j}$
imposes one condition on the family of maps
![]() $f|_C$
. Since our original curve
$f|_C$
. Since our original curve
![]() $(C,q_{1},\ldots ,q_{m})$
is general in moduli, the conditions imposed at all such
$(C,q_{1},\ldots ,q_{m})$
is general in moduli, the conditions imposed at all such
![]() $q_i$
are independent. Therefore, we conclude that the dimension of the image of
$q_i$
are independent. Therefore, we conclude that the dimension of the image of
![]() $M_{m,0}$
under
$M_{m,0}$
under
![]() $\phi $
is at most
$\phi $
is at most
 $$ \begin{align*} d_0+O(1)+c+2s+2s' &=d-(c+s_+)+O(1)\\ &=3m-b+O(1). \end{align*} $$
$$ \begin{align*} d_0+O(1)+c+2s+2s' &=d-(c+s_+)+O(1)\\ &=3m-b+O(1). \end{align*} $$
On the other hand, in order for
![]() $M_{m, 0}$
to dominate
$M_{m, 0}$
to dominate
![]() $X^{\times m}$
, we need
$X^{\times m}$
, we need
hence
![]() $b\le O(1)$
. In particular,
$b\le O(1)$
. In particular,
![]() $m-b\ge g+1$
if m is sufficiently large. Then, by Lemma 4.1, it follows that
$m-b\ge g+1$
if m is sufficiently large. Then, by Lemma 4.1, it follows that
![]() $f|_{C}$
moves in a family of the expected dimension of
$f|_{C}$
moves in a family of the expected dimension of
![]() $d_0-3g+3$
(we have subtracted
$d_0-3g+3$
(we have subtracted
![]() $3g-3+m$
from the right-hand side of the formula of Lemma 4.1 to account for the fact that we have fixed the moduli of C). We now repeat the calculation of the dimension of the space of deformations of f, with this more precise estimate. The dimension of the image of
$3g-3+m$
from the right-hand side of the formula of Lemma 4.1 to account for the fact that we have fixed the moduli of C). We now repeat the calculation of the dimension of the space of deformations of f, with this more precise estimate. The dimension of the image of
![]() $M_{m,0}$
under
$M_{m,0}$
under
![]() $\phi $
is at most
$\phi $
is at most
 $$ \begin{align*} (d_0-3g+3)+c+2s_+&=(d-3g+3)-(c+s_+)\\ &=(d-3g+3)-b, \end{align*} $$
$$ \begin{align*} (d_0-3g+3)+c+2s_+&=(d-3g+3)-(c+s_+)\\ &=(d-3g+3)-b, \end{align*} $$
which is b less than the expected dimension. Thus, the deformations of f cannot dominate
![]() $X^{\times m}$
, which has dimension
$X^{\times m}$
, which has dimension
![]() $3m>(d-3g+3)-b$
.
$3m>(d-3g+3)-b$
.
Case 3:
![]() $\dim (Z)=1$
.
$\dim (Z)=1$
.
As in the case where C is contracted, we need
![]() $c=0$
since a free conic through a general point does not meet a fixed curve
$c=0$
since a free conic through a general point does not meet a fixed curve
![]() $Z\subset X$
. Also, we need
$Z\subset X$
. Also, we need
![]() $b=m$
or else C sweeps out all of X. Thus,
$b=m$
or else C sweeps out all of X. Thus,
and in particular, the space of deformations of
![]() $f|_{C}$
has bounded dimension
$f|_{C}$
has bounded dimension
![]() $O(1)$
. First, suppose that a general point of Z is not contained in a one-parameter family of lines. Then arguing in the previous case, the space of deformations of f has dimension at most
$O(1)$
. First, suppose that a general point of Z is not contained in a one-parameter family of lines. Then arguing in the previous case, the space of deformations of f has dimension at most
Thus, this space of deformations cannot dominate
![]() $X^{\times m}$
.
$X^{\times m}$
.
On the other hand, if a general (and hence, every) point of Z is contained in a one-parameter family of lines, then these lines must sweep out a surface Y carrying a two-dimensional family of lines. By [Reference Beheshti, Lehmann, Riedl and TanimotoBLRT22, Lemma 4.4], Y is an E5 divisor, and we are now in case (ii) of the theorem.
Case 4:
![]() $\dim (Z)=2$
.
$\dim (Z)=2$
.
Let
![]() $\psi : \widetilde {Z} \to X$
denote the composition of a resolution of Z with the inclusion. Let
$\psi : \widetilde {Z} \to X$
denote the composition of a resolution of Z with the inclusion. Let
![]() $\widetilde {f}: C\to \widetilde {Z}$
be the map obtained by strict transform from a general point of
$\widetilde {f}: C\to \widetilde {Z}$
be the map obtained by strict transform from a general point of
![]() $M_{m, 0}$
over
$M_{m, 0}$
over
![]() $(C,q_1,\ldots ,q_m)$
. Then, by Lemma 4.2, the map
$(C,q_1,\ldots ,q_m)$
. Then, by Lemma 4.2, the map
![]() $\widetilde {f}$
moves in a family of dimension at most
$\widetilde {f}$
moves in a family of dimension at most
Suppose for a contradiction that we have
![]() $a(\widetilde {Z},\psi ^{*}(-K_{X})) < 2$
. Since deformations of C sweep out Z, we have
$a(\widetilde {Z},\psi ^{*}(-K_{X})) < 2$
. Since deformations of C sweep out Z, we have
Choose
![]() $\epsilon> 0$
so that
$\epsilon> 0$
so that
![]() $2 - \epsilon> a(\widetilde {Z},\psi ^{*}(-K_{X}))$
. Then for any
$2 - \epsilon> a(\widetilde {Z},\psi ^{*}(-K_{X}))$
. Then for any
![]() $O(1)$
constants, we find that in sufficiently large degrees
$O(1)$
constants, we find that in sufficiently large degrees
where
![]() $d_0=-K_X\cdot f_{*}[C]$
as before. The same estimate also gives an upper bound on the dimension of the space of deformations of
$d_0=-K_X\cdot f_{*}[C]$
as before. The same estimate also gives an upper bound on the dimension of the space of deformations of
![]() $f|_{C}:C\to Z$
.
$f|_{C}:C\to Z$
.
Consider now the space of deformations of f. As in case 2, the free conics and cubics add one and two parameters, respectively. We claim that reducible chains of the form
![]() $T_i=L_i\cup C_i$
also add two parameters. First, suppose that
$T_i=L_i\cup C_i$
also add two parameters. First, suppose that
![]() $f(q_i)$
is contained in a 1-parameter family of lines. Then, because
$f(q_i)$
is contained in a 1-parameter family of lines. Then, because
![]() $f(q_i)$
is a general point of the divisor Z, and a family of lines cannot cover X, this one-parameter family of lines must be contained in Z and thus sweeps out Z. Therefore, the lines have anticanonical degree at least 2 on
$f(q_i)$
is a general point of the divisor Z, and a family of lines cannot cover X, this one-parameter family of lines must be contained in Z and thus sweeps out Z. Therefore, the lines have anticanonical degree at least 2 on
![]() $\widetilde {Z}$
, which contradicts the assumption that
$\widetilde {Z}$
, which contradicts the assumption that
![]() $a(Z,-K_{X}|_Z) < 2$
. Thus, only finitely many lines pass through
$a(Z,-K_{X}|_Z) < 2$
. Thus, only finitely many lines pass through
![]() $f(q_i)$
. Then, there is a one-parameter family of free conics
$f(q_i)$
. Then, there is a one-parameter family of free conics
![]() $C_i$
incident to
$C_i$
incident to
![]() $L_i$
, and there is a one-parameter family of points on
$L_i$
, and there is a one-parameter family of points on
![]() $C_i$
. In total, the chains
$C_i$
. In total, the chains
![]() $T_i$
also add two parameters to the space of deformations of f.
$T_i$
also add two parameters to the space of deformations of f.
We conclude that the space of deformations of f has dimension at most
 $$ \begin{align*} (2-\epsilon)(d-2c-3s_+)+O(1)+c+2s_+&\le (2-\epsilon)(3m-2c-3s_+)+c+2s_{+}+O(1)\\ &=(6-3\epsilon)m-(3-2\epsilon)c-(4-3\epsilon)s_{+}+O(1)\\ &=(3-\epsilon)m-(1-\epsilon)s_{+}+O(1) \\ & <3m, \end{align*} $$
$$ \begin{align*} (2-\epsilon)(d-2c-3s_+)+O(1)+c+2s_+&\le (2-\epsilon)(3m-2c-3s_+)+c+2s_{+}+O(1)\\ &=(6-3\epsilon)m-(3-2\epsilon)c-(4-3\epsilon)s_{+}+O(1)\\ &=(3-\epsilon)m-(1-\epsilon)s_{+}+O(1) \\ & <3m, \end{align*} $$
for m sufficiently large. In the next-to-last line, we have used the equality
![]() $c+s_{+} = b = m$
. In the last line, we have used the fact that
$c+s_{+} = b = m$
. In the last line, we have used the fact that
![]() $(1-\epsilon )s_{+}\ge 0$
if
$(1-\epsilon )s_{+}\ge 0$
if
![]() $\epsilon \le 1$
, whereas if
$\epsilon \le 1$
, whereas if
![]() $\epsilon>1$
, then
$\epsilon>1$
, then
![]() $(3-\epsilon )m-(1-\epsilon )s_+=2m+(1-\epsilon )(m-s_+)<2m$
. Thus,
$(3-\epsilon )m-(1-\epsilon )s_+=2m+(1-\epsilon )(m-s_+)<2m$
. Thus,
![]() $M_{m, 0}$
cannot dominate
$M_{m, 0}$
cannot dominate
![]() $X^{\times m}$
.
$X^{\times m}$
.
Proof of Theorem 1.10
Let X be a smooth Fano threefold, and assume first that there is an infinite sequence of positive integers m and nef curve classes
![]() $\beta $
on X such that
$\beta $
on X such that
![]() $(g,-K_{X} \cdot \beta ,m)$
is a fixed-domain triple and a sequence of irreducible components
$(g,-K_{X} \cdot \beta ,m)$
is a fixed-domain triple and a sequence of irreducible components
![]() $M_m \subset \overline {\mathcal {M}}_{g,m}(X,\beta )$
such that a general fiber of the morphism
$M_m \subset \overline {\mathcal {M}}_{g,m}(X,\beta )$
such that a general fiber of the morphism
![]() $M_m \to \overline {\mathcal {M}}_{g,m} \times X^{\times m}$
consists only of maps with reducible domains. By Theorem 4.3, X admits a divisor Y with
$M_m \to \overline {\mathcal {M}}_{g,m} \times X^{\times m}$
consists only of maps with reducible domains. By Theorem 4.3, X admits a divisor Y with
![]() $a(Y,-K_{X}|_{Y}) \geq 2$
.
$a(Y,-K_{X}|_{Y}) \geq 2$
.
According to [Reference Beheshti, Lehmann, Riedl and TanimotoBLRT22, Theorem 4.1], if X is a smooth Fano threefold and
![]() $Y \subset X$
is a surface satisfying
$Y \subset X$
is a surface satisfying
![]() $a(Y,-K_{X}|_{Y})> 1$
, then either Y is swept out by anticanonical lines or Y is an exceptional divisor on X. The exceptional divisors with Fujita invariant
$a(Y,-K_{X}|_{Y})> 1$
, then either Y is swept out by anticanonical lines or Y is an exceptional divisor on X. The exceptional divisors with Fujita invariant
![]() $\geq 2$
have types E1, E3, E4, E5, and each admits a dominant family of anticanonical lines.
$\geq 2$
have types E1, E3, E4, E5, and each admits a dominant family of anticanonical lines.
Therefore, if X is a smooth Fano threefold without a divisor Y as in the statement of Theorem 1.10, then a general fiber of the morphism
![]() $\overline {\mathcal {M}}_{g,m}(X,\beta ) \to \overline {\mathcal {M}}_{g,m} \times X^{\times m}$
consists only of maps with irreducible (hence smooth) domains, for any fixed-domain triple
$\overline {\mathcal {M}}_{g,m}(X,\beta ) \to \overline {\mathcal {M}}_{g,m} \times X^{\times m}$
consists only of maps with irreducible (hence smooth) domains, for any fixed-domain triple
![]() $(g,-K_{X} \cdot \beta ,m)$
with m sufficiently large compared to g. By [Reference Lian and PandharipandeLP23, Proposition 13 and Proposition 14], the generic fiber of
$(g,-K_{X} \cdot \beta ,m)$
with m sufficiently large compared to g. By [Reference Lian and PandharipandeLP23, Proposition 13 and Proposition 14], the generic fiber of
![]() $\phi $
is furthermore reduced of dimension 0. It follows that X satisfies asymptotic enumerativity.
$\phi $
is furthermore reduced of dimension 0. It follows that X satisfies asymptotic enumerativity.
When X is a smooth Fano threefold which carries a divisor swept out by lines it is usually straightforward to tell directly whether one can obstruct asymptotic enumerativity using stable maps consisting of rational curves attached to a central genus g curve C as described by Theorem 4.3.
Example 4.4. Consider the Fano threefold
![]() $X = \mathbb {P}_{\mathbb {P}^{2}}(\mathcal {O} \oplus \mathcal {O}(2))$
. The rigid section Z of the
$X = \mathbb {P}_{\mathbb {P}^{2}}(\mathcal {O} \oplus \mathcal {O}(2))$
. The rigid section Z of the
![]() $\mathbb {P}^{1}$
-bundle
$\mathbb {P}^{1}$
-bundle
![]() $X \to \mathbb {P}^{2}$
is an E5 divisor with Fujita invariant 3. Proposition 3.7 demonstrated the failure of asymptotic enumerativity on X using the existence of the divisor Z. As predicted by Theorem 4.3, the ‘bad’ curves are obtained by attaching m fibers of the projective bundle to a genus g curve in Z.
$X \to \mathbb {P}^{2}$
is an E5 divisor with Fujita invariant 3. Proposition 3.7 demonstrated the failure of asymptotic enumerativity on X using the existence of the divisor Z. As predicted by Theorem 4.3, the ‘bad’ curves are obtained by attaching m fibers of the projective bundle to a genus g curve in Z.
Example 4.5. Let
![]() $X\subset {\mathbb P}^4$
be a conical quartic threefold. Then X fails to satisfy asymptotic enumerativity by Example 3.5. By definition the conical divisor of X contains a one-parameter family of lines through the cone point p. As predicted by the proof of Theorem 4.3, asymptotic enumerativity is violated by curves
$X\subset {\mathbb P}^4$
be a conical quartic threefold. Then X fails to satisfy asymptotic enumerativity by Example 3.5. By definition the conical divisor of X contains a one-parameter family of lines through the cone point p. As predicted by the proof of Theorem 4.3, asymptotic enumerativity is violated by curves
![]() $\widetilde {C}$
for which the central genus g curve C is contracted to p.
$\widetilde {C}$
for which the central genus g curve C is contracted to p.
Example 4.6. Let X be the Fano threefold
![]() ${\mathbb P}_{{\mathbb P}^1\times {\mathbb P}^1}(\mathcal {\mathcal O} \oplus \mathcal {\mathcal O}(1,1))$
, and let
${\mathbb P}_{{\mathbb P}^1\times {\mathbb P}^1}(\mathcal {\mathcal O} \oplus \mathcal {\mathcal O}(1,1))$
, and let
![]() $\pi :X\to {\mathbb P}^1\times {\mathbb P}^1$
be the projection. Let
$\pi :X\to {\mathbb P}^1\times {\mathbb P}^1$
be the projection. Let
![]() $Z\subset X$
be the section of
$Z\subset X$
be the section of
![]() $\pi $
corresponding to the projection
$\pi $
corresponding to the projection
![]() ${\mathcal O} \oplus \mathcal {\mathcal O}(1,1)\to {\mathcal O}$
. Then Z is an E1 divisor with Fujita invariant 2. However, no point on Z (or X) is contained in a one-parameter family of lines.
${\mathcal O} \oplus \mathcal {\mathcal O}(1,1)\to {\mathcal O}$
. Then Z is an E1 divisor with Fujita invariant 2. However, no point on Z (or X) is contained in a one-parameter family of lines.
Repeating the contruction of §3.2, for any positive integer m with
![]() $m+g\equiv 1\pmod {2}$
, we construct reducible curves of genus g with general moduli through m general points of
$m+g\equiv 1\pmod {2}$
, we construct reducible curves of genus g with general moduli through m general points of
![]() $p_i\in X$
of anticanonical degree
$p_i\in X$
of anticanonical degree
![]() $3m+g-1$
as follows. Attach a
$3m+g-1$
as follows. Attach a
![]() $\left (\frac {m+g-1}{2},\frac {m+g-1}{2}\right )$
-curve of genus g in
$\left (\frac {m+g-1}{2},\frac {m+g-1}{2}\right )$
-curve of genus g in
![]() $Z\cong {\mathbb P}^1\times {\mathbb P}^1$
at the points
$Z\cong {\mathbb P}^1\times {\mathbb P}^1$
at the points
![]() $q_i\in C$
to rational tails mapping isomorphically to the fibers of
$q_i\in C$
to rational tails mapping isomorphically to the fibers of
![]() $\pi $
over the
$\pi $
over the
![]() $p_i$
. Such a curve with general moduli in Z exists, for example, by [Reference LarsonLar16, Corollary 1.3]. If
$p_i$
. Such a curve with general moduli in Z exists, for example, by [Reference LarsonLar16, Corollary 1.3]. If
![]() $g>0$
, then one may replace the rational tails with multiple covers of arbitrary degree to obtain a map of degree exactly
$g>0$
, then one may replace the rational tails with multiple covers of arbitrary degree to obtain a map of degree exactly
![]() $3m+3g-3$
. In this way, X fails to satisfy asymptotic enumerativity for any
$3m+3g-3$
. In this way, X fails to satisfy asymptotic enumerativity for any
![]() $g>0$
.
$g>0$
.
The following example shows that a Fano threefold can satisfy asymptotic enumerativity in every genus even if it carries a divisor with Fujita invariant
![]() $2$
.
$2$
.
Example 4.7. Let X be the blowup of
![]() $\mathbb {P}^{3}$
along the intersection Z of a smooth quadric and a smooth cubic. Then X carries two divisors with Fujita invariant
$\mathbb {P}^{3}$
along the intersection Z of a smooth quadric and a smooth cubic. Then X carries two divisors with Fujita invariant
![]() $2$
: the exceptional divisor E for the blowup (of type E1) and the strict transform Q of the quadric (of type E3). However, no point of X is contained in a one-parameter family of lines.
$2$
: the exceptional divisor E for the blowup (of type E1) and the strict transform Q of the quadric (of type E3). However, no point of X is contained in a one-parameter family of lines.
We claim that X satisfies asymptotic enumerativity in every genus. By Theorem 4.3, it suffices to show that asymptotic enumerativity cannot be violated by families of reducible curves where the central genus g curve C deforms to sweep out Q or E.
First, we show that it is not possible to obstruct asymptotic enumerativity using a family of reducible curves
![]() $\widetilde {C}$
such that the genus g component C sweeps out Q. The only dominant family of anticanonical conics T on X is given by the strict transforms of lines meeting Z twice. For every such curve,
$\widetilde {C}$
such that the genus g component C sweeps out Q. The only dominant family of anticanonical conics T on X is given by the strict transforms of lines meeting Z twice. For every such curve,
![]() $Q \cdot T = 0$
and thus a general conic cannot meet Q. To finish the argument, we repeat the computation in Case 4 of the proof of Theorem 4.3. In the notation of this proof, we have shown that
$Q \cdot T = 0$
and thus a general conic cannot meet Q. To finish the argument, we repeat the computation in Case 4 of the proof of Theorem 4.3. In the notation of this proof, we have shown that
![]() $c = 0$
so that
$c = 0$
so that
![]() $s_{+} = m$
. The computation in this proof shows that curves of this type deform in dimension at most
$s_{+} = m$
. The computation in this proof shows that curves of this type deform in dimension at most
![]() $2m + O(1)$
. Since the dimension of
$2m + O(1)$
. Since the dimension of
![]() $X^{\times m}$
is
$X^{\times m}$
is
![]() $3m$
, we see that asymptotic enumerativity cannot be violated using such curves.
$3m$
, we see that asymptotic enumerativity cannot be violated using such curves.
Next, we show that it is not possible to obstruct asymptotic enumerativity using a family of reducible curves
![]() $\widetilde {C}$
such that the genus g component C sweeps out E. Since Z has genus
$\widetilde {C}$
such that the genus g component C sweeps out E. Since Z has genus
![]() $4$
, it does not receive a map from a general curve of genus g for any g. Thus, the only way to violate enumerativity using maps to E is if C is a multiple cover of a fiber of
$4$
, it does not receive a map from a general curve of genus g for any g. Thus, the only way to violate enumerativity using maps to E is if C is a multiple cover of a fiber of
![]() $E \to Z$
or is contracted to a point. Note that such a curve can meet at most one general anticanonical conic. Repeating the computation in Case 4 of the proof of Theorem 4.3, we see that
$E \to Z$
or is contracted to a point. Note that such a curve can meet at most one general anticanonical conic. Repeating the computation in Case 4 of the proof of Theorem 4.3, we see that
![]() $s_{+} \geq m-1$
so that curves of this type deform in dimension at most
$s_{+} \geq m-1$
so that curves of this type deform in dimension at most
![]() $2m + O(1)$
. Thus, asymptotic enumerativity cannot be violated using such curves.
$2m + O(1)$
. Thus, asymptotic enumerativity cannot be violated using such curves.
5 Hypersurfaces
The goal in this section is to prove the following theorem describing enumerativity of fixed-domain GW invariants for certain hypersurfaces.
Theorem 5.1. Suppose X is a smooth hypersurface of degree d in
![]() $\mathbb {P}^n$
such that
$\mathbb {P}^n$
such that
-
(1)
 $d \leq n-2$
and X is general, or
$d \leq n-2$
and X is general, or -
(2)
 $d \leq (n+3)/3$
.
$d \leq (n+3)/3$
.
Then X satisfies asymptotic enumerativity for every genus g.
The strategy of proof is as follows. It is enough to establish an upper bound, independent of g, on
![]() $h^1$
of the restricted tangent bundle for a stable map of genus g to X with general stabilized domain passing through m points. (See Lemma 5.4 for a precise statement.) We obtain such a bound by degeneration. When
$h^1$
of the restricted tangent bundle for a stable map of genus g to X with general stabilized domain passing through m points. (See Lemma 5.4 for a precise statement.) We obtain such a bound by degeneration. When
![]() $g=0$
, we replace the general domain curve with a maximally degenerate chain of rational curves, see Lemma 5.5 and Proposition 5.6, using results established in §5.1 to obtain bounds on
$g=0$
, we replace the general domain curve with a maximally degenerate chain of rational curves, see Lemma 5.5 and Proposition 5.6, using results established in §5.1 to obtain bounds on
![]() $h^1$
. The case of arbitrary genus is finally reduced to the case of genus
$h^1$
. The case of arbitrary genus is finally reduced to the case of genus
![]() $0$
by replacing a general pointed curve of genus g by one with a rational tail containing all of the marked points.
$0$
by replacing a general pointed curve of genus g by one with a rational tail containing all of the marked points.
In this section, we will say that a rational curve
![]() $C \subset X$
is a line or conic if C is a line or conic in the ambient projective space.
$C \subset X$
is a line or conic if C is a line or conic in the ambient projective space.
5.1 Chains of curves on hypersurfaces
Let X be a smooth hypersurface of degree d in
![]() $\mathbb {P}^n$
. We assume throughout that
$\mathbb {P}^n$
. We assume throughout that
![]() $d\le n$
and that
$d\le n$
and that
![]() $n\ge 4$
. By the parameter space of chains of rational curves of degree e with t components, we mean the closure of the locus in
$n\ge 4$
. By the parameter space of chains of rational curves of degree e with t components, we mean the closure of the locus in
![]() $\overline {M}_{0,0}(X,e)$
parametrizing stable maps
$\overline {M}_{0,0}(X,e)$
parametrizing stable maps
![]() $f: C \to X$
of degree e such that C is a chain
$f: C \to X$
of degree e such that C is a chain
![]() $C=C_1 \cup \dots \cup C_t$
of t smooth rational curves such that
$C=C_1 \cup \dots \cup C_t$
of t smooth rational curves such that
![]() $C_i$
intersects
$C_i$
intersects
![]() $C_{i-1}$
and
$C_{i-1}$
and
![]() $C_{i+1}$
. The expected dimension of the parameter space of chains of rational curves on X of degree e with t components is
$C_{i+1}$
. The expected dimension of the parameter space of chains of rational curves on X of degree e with t components is
When X is general and
![]() $d\leq n-2$
, by [Reference Riedl and YangRY19, Theorem 3.3], the space of rational curves of a given degree through any point of X has the expected dimension
$d\leq n-2$
, by [Reference Riedl and YangRY19, Theorem 3.3], the space of rational curves of a given degree through any point of X has the expected dimension
![]() $e(n+1-d)-2$
, so every component of the parameter space of chains of rational curves in X has the expected dimension.
$e(n+1-d)-2$
, so every component of the parameter space of chains of rational curves in X has the expected dimension.
Proposition 5.2. If
![]() $X \subset \mathbb {P}^n$
is a smooth hypersurface of degree d, then the space of nonfree lines on X has dimension at most
$X \subset \mathbb {P}^n$
is a smooth hypersurface of degree d, then the space of nonfree lines on X has dimension at most
![]() $n+d-5$
.
$n+d-5$
.
Proof. Suppose S is a family of nonfree lines sweeping out an irreducible subvariety Y in X. Let l be a general line parametrized by S. Then by [Reference Beheshti and RiedlBR21, Theorem 2.4],
![]() $\dim S \leq \dim Y +n-3-h^0(N_{l/X}(-1)) \leq 2n-5-h^0(N_{l/X}(-1))$
. Since l is not free, the proof of [Reference Beheshti and RiedlBR21, Theorem 2.4] shows that
$\dim S \leq \dim Y +n-3-h^0(N_{l/X}(-1)) \leq 2n-5-h^0(N_{l/X}(-1))$
. Since l is not free, the proof of [Reference Beheshti and RiedlBR21, Theorem 2.4] shows that
![]() $h^0(N_{l/X}(-1)) \geq n-d$
and we get the desired result.
$h^0(N_{l/X}(-1)) \geq n-d$
and we get the desired result.
Proposition 5.3. Let
![]() $X \subset \mathbb {P}^n$
be any smooth hypersurface of degree
$X \subset \mathbb {P}^n$
be any smooth hypersurface of degree
![]() $d\leq (n+3)/3$
. Then every irreducible component of the space parametrizing chains of lines and free conics has the expected dimension.
$d\leq (n+3)/3$
. Then every irreducible component of the space parametrizing chains of lines and free conics has the expected dimension.
Proof. We argue by induction on the number of irreducible components t in the chain. If
![]() $t=1$
, then we either have a line or a free conic. By [Reference Beheshti and RiedlBR21, Theorem 1.3], the space of lines has the expected dimension
$t=1$
, then we either have a line or a free conic. By [Reference Beheshti and RiedlBR21, Theorem 1.3], the space of lines has the expected dimension
![]() $2n-d-3$
for every smooth hypersurface of degree
$2n-d-3$
for every smooth hypersurface of degree
![]() $\leq (n+4)/2$
. Thus, in both cases the dimension is the expected dimension.
$\leq (n+4)/2$
. Thus, in both cases the dimension is the expected dimension.
For the induction step, suppose the statement holds for
![]() $t' < t$
. Write
$t' < t$
. Write
![]() $\widetilde {C}=C_1 \cup \dots \cup C_t$
for the irreducible components of
$\widetilde {C}=C_1 \cup \dots \cup C_t$
for the irreducible components of
![]() $\widetilde {C}$
. First, suppose that
$\widetilde {C}$
. First, suppose that
![]() $C_t$
is a free conic or a free line. By induction, the deformation space of the chain of curves
$C_t$
is a free conic or a free line. By induction, the deformation space of the chain of curves
![]() $C_{1} \cup \ldots \cup C_{t-1}$
has the expected dimension. Since we are attaching a free curve to this chain, the total family also has the expected dimension. Indeed, the deformation space of the free curve has the expected dimension, and the requirement that the free curve be incident to the chain at any fixed point also imposes the expected number of conditions on the free curve.
$C_{1} \cup \ldots \cup C_{t-1}$
has the expected dimension. Since we are attaching a free curve to this chain, the total family also has the expected dimension. Indeed, the deformation space of the free curve has the expected dimension, and the requirement that the free curve be incident to the chain at any fixed point also imposes the expected number of conditions on the free curve.
Next, suppose
![]() $C_t$
is a nonfree line. There are two cases:
$C_t$
is a nonfree line. There are two cases:
-
•
 $C_{t-1}$
is a line: In this case, the space of deformations of
$C_{t-1}$
is a line: In this case, the space of deformations of
 $C_1 \cup \dots \cup C_{t-2}$
has dimension at most
$C_1 \cup \dots \cup C_{t-2}$
has dimension at most
 $(e-2)(n+1-d)+n-3-(t-2)$
by our induction hypothesis, and the space of nonfree lines has dimension
$(e-2)(n+1-d)+n-3-(t-2)$
by our induction hypothesis, and the space of nonfree lines has dimension
 $\leq n+d-5$
by Proposition 5.2. Since we are assuming that
$\leq n+d-5$
by Proposition 5.2. Since we are assuming that
 $d \leq (n+3)/3$
, the total dimension is at most where the terms in brackets come from the deformations of the chain and the component
$d \leq (n+3)/3$
, the total dimension is at most where the terms in brackets come from the deformations of the chain and the component $$ \begin{align*} &[(e-2)(n+1-d)+n-3-(t-2)]+1+[n+d-5]+1 \\ \leq \quad &e(n+1-d)+n-3-t, \end{align*} $$
$$ \begin{align*} &[(e-2)(n+1-d)+n-3-(t-2)]+1+[n+d-5]+1 \\ \leq \quad &e(n+1-d)+n-3-t, \end{align*} $$
 $C_{t-1}$
, respectively, and the additional summands
$C_{t-1}$
, respectively, and the additional summands
 $+1$
from the possible degrees of freedom from the points to which these components are attached.
$+1$
from the possible degrees of freedom from the points to which these components are attached.
-
•
 $C_{t-1}$
is a free conic: The argument is similar to the previous case. First, note that the space of free conics through any two fixed points of X has dimension
$C_{t-1}$
is a free conic: The argument is similar to the previous case. First, note that the space of free conics through any two fixed points of X has dimension
 $\leq n-d+1$
. Indeed,
$\leq n-d+1$
. Indeed,
 $N_{C/X}$
is a subbundle of
$N_{C/X}$
is a subbundle of
 $N_{C/{\mathbb P}^n}={\mathcal O}(4) \oplus {\mathcal O}(2)^{n-2}$
of degree
$N_{C/{\mathbb P}^n}={\mathcal O}(4) \oplus {\mathcal O}(2)^{n-2}$
of degree
 $2n-2d$
with no negative summand. Thus,
$2n-2d$
with no negative summand. Thus,
 $N_{C/X}(-2)$
has either: 1) at most
$N_{C/X}(-2)$
has either: 1) at most
 $n-d$
summands of degree
$n-d$
summands of degree
 $0$
and all the other summands negative or 2) at most
$0$
and all the other summands negative or 2) at most
 $n-d-2$
summands of degree
$n-d-2$
summands of degree
 $0$
,
$0$
,
 $1$
summand of degree
$1$
summand of degree
 $2$
, and all the rest negative. In both cases,
$2$
, and all the rest negative. In both cases,
 $H^{0}(C,N_{C/X}(-2))$
is at most
$H^{0}(C,N_{C/X}(-2))$
is at most
 $n-d+1$
.
$n-d+1$
.By our induction hypothesis, the space of deformations of
 $C_1 \cup \dots \cup C_{t-2}$
has dimension at most
$C_1 \cup \dots \cup C_{t-2}$
has dimension at most
 $(e-3)(n+1-d)+n-3-(t-2)$
. By choosing the connection points of the free conic
$(e-3)(n+1-d)+n-3-(t-2)$
. By choosing the connection points of the free conic
 $C_{t-1}$
with the curves
$C_{t-1}$
with the curves
 $C_{t-2}, C_{t}$
, we get that the dimension of the space of such chains is at most
$C_{t-2}, C_{t}$
, we get that the dimension of the space of such chains is at most  $$ \begin{align*} &[(e-3)(n+1-d)+n-3-(t-2)]+1+[n+d-5]+1+[n-d+1] \\ \leq\quad & e(n+1-d)+n-3-t.\\[-42pt] \end{align*} $$
$$ \begin{align*} &[(e-3)(n+1-d)+n-3-(t-2)]+1+[n+d-5]+1+[n-d+1] \\ \leq\quad & e(n+1-d)+n-3-t.\\[-42pt] \end{align*} $$
5.2 Asymptotic enumerativity for hypersurfaces
We build up the proof of Theorem 5.1 in several steps. Consider the map
Lemma 5.4. Let X be a smooth hypersurface of degree d in
![]() $\mathbb {P}^{n}$
and fix a genus g.
$\mathbb {P}^{n}$
and fix a genus g.
Suppose that there is a constant A depending only on X and g such that, for any positive integers
![]() $m,e$
with
$m,e$
with
![]() $e(n+1-d)=(n-1)(m+g-1)$
, for a general
$e(n+1-d)=(n-1)(m+g-1)$
, for a general
![]() $([C], p_1, \dots , p_m) \in \overline {{\mathcal M}}_{g,m}\times X^{\times m}$
, and for any
$([C], p_1, \dots , p_m) \in \overline {{\mathcal M}}_{g,m}\times X^{\times m}$
, and for any
![]() $(\widetilde {C}, f, \widetilde {q}_1, \dots , \widetilde {q}_m)$
in the fiber of
$(\widetilde {C}, f, \widetilde {q}_1, \dots , \widetilde {q}_m)$
in the fiber of
![]() $\phi $
over
$\phi $
over
![]() $([C],p_1,\dots ,p_m)$
, we have
$([C],p_1,\dots ,p_m)$
, we have
![]() $h^1(\widetilde {C},f^*T_X)\le A$
.
$h^1(\widetilde {C},f^*T_X)\le A$
.
Suppose further that X satisfies one of the hypotheses (1), (2) of Theorem 5.1. Then, Theorem 5.1 holds for X and genus g.
Proof. Suppose otherwise. Then, for arbitrarily large m and e and for general
![]() $([C], p_1, \dots , p_m) \in \overline {{\mathcal M}}_{g,m}\times X^{\times m}$
, there exist
$([C], p_1, \dots , p_m) \in \overline {{\mathcal M}}_{g,m}\times X^{\times m}$
, there exist
![]() $(\widetilde {C}, f, \widetilde {q}_1, \dots , \widetilde {q}_m)$
in the fiber of
$(\widetilde {C}, f, \widetilde {q}_1, \dots , \widetilde {q}_m)$
in the fiber of
![]() $\phi $
such that
$\phi $
such that
![]() $\widetilde {C}$
is reducible. Indeed, when
$\widetilde {C}$
is reducible. Indeed, when
![]() $\widetilde {C}$
is irreducible, our assertion follows from [Reference Lian and PandharipandeLP23, Proposition 13 and Proposition 14]. It follows that
$\widetilde {C}$
is irreducible, our assertion follows from [Reference Lian and PandharipandeLP23, Proposition 13 and Proposition 14]. It follows that
![]() $\widetilde {C}$
has a component isomorphic to C, to which trees of rational curves, each containing at most one marked point, are attached. Assume without loss of generality that the first t marked points are on the attached trees and the last
$\widetilde {C}$
has a component isomorphic to C, to which trees of rational curves, each containing at most one marked point, are attached. Assume without loss of generality that the first t marked points are on the attached trees and the last
![]() $m-t$
marked points are on C; see Figure 4.
$m-t$
marked points are on C; see Figure 4.

Figure 4 The curve
![]() $\widetilde {C}$
, obtained from C by attaching rational trees.
$\widetilde {C}$
, obtained from C by attaching rational trees.
Let
![]() $\iota :C\to \widetilde {C}$
be the natural closed embedding. From the surjection
$\iota :C\to \widetilde {C}$
be the natural closed embedding. From the surjection
![]() $f^{*}T_X\to \iota _{*}\iota ^{*}f^{*}T_X$
of sheaves on
$f^{*}T_X\to \iota _{*}\iota ^{*}f^{*}T_X$
of sheaves on
![]() $\widetilde {C}$
, we have
$\widetilde {C}$
, we have
First, suppose that
![]() $d<(n+3)/2$
. Then, as X has Fano index at least
$d<(n+3)/2$
. Then, as X has Fano index at least
![]() $n/2$
, the hypothesis (ii) from [Reference Lian and PandharipandeLP23, Proposition 22] is satisfied. Furthermore, because
$n/2$
, the hypothesis (ii) from [Reference Lian and PandharipandeLP23, Proposition 22] is satisfied. Furthermore, because
![]() $h^1(C,f^{*}T_X|_{C}) \le A$
, we have condition
$h^1(C,f^{*}T_X|_{C}) \le A$
, we have condition
![]() $(\star )_g$
, hence condition
$(\star )_g$
, hence condition
![]() $(\star \star )_g$
; see [Reference Lian and PandharipandeLP23, Definition 18], at least upon restriction to f over a general point of
$(\star \star )_g$
; see [Reference Lian and PandharipandeLP23, Definition 18], at least upon restriction to f over a general point of
![]() $\phi $
. Therefore, [Reference Lian and PandharipandeLP23, Proposition 22] (which only requires working over a general point of
$\phi $
. Therefore, [Reference Lian and PandharipandeLP23, Proposition 22] (which only requires working over a general point of
![]() $\phi $
) applies, and the conclusion of Theorem 5.1 follows. In particular, if X has degree
$\phi $
) applies, and the conclusion of Theorem 5.1 follows. In particular, if X has degree
![]() $d \leq (n+3)/3$
, then we obtain the conclusion.
$d \leq (n+3)/3$
, then we obtain the conclusion.
Now, suppose that
![]() $d\le n-2$
and that X is general. Let
$d\le n-2$
and that X is general. Let
![]() $C'$
be the connected curve obtained by successively deleting components on the attached trees which do not contain a marked point and whose removal does not make the tree disconnected. Let
$C'$
be the connected curve obtained by successively deleting components on the attached trees which do not contain a marked point and whose removal does not make the tree disconnected. Let
![]() $e_i$
be the degree of f restricted to the irreducible component containing the ith marked point for
$e_i$
be the degree of f restricted to the irreducible component containing the ith marked point for
![]() $1 \leq i \leq t$
. Let
$1 \leq i \leq t$
. Let
![]() $C"$
be the curve obtained by removing the components with marked points on the attached trees in
$C"$
be the curve obtained by removing the components with marked points on the attached trees in
![]() $C'$
, and suppose the total degree of
$C'$
, and suppose the total degree of
![]() $f|_{C^{\prime \prime }}$
is
$f|_{C^{\prime \prime }}$
is
![]() $e^{\prime \prime }$
. The curves
$e^{\prime \prime }$
. The curves
![]() $C',C"$
are depicted in Figure 5.
$C',C"$
are depicted in Figure 5.

Figure 5 The curves
![]() $C'$
(left) and
$C'$
(left) and
![]() $C"$
(right), obtained by deleting components from
$C"$
(right), obtained by deleting components from
![]() $\widetilde {C}$
.
$\widetilde {C}$
.
Because
![]() $h^1(C",f^*T_X|_{C^{\prime \prime }})\le A$
, we have that
$h^1(C",f^*T_X|_{C^{\prime \prime }})\le A$
, we have that
![]() $f|_{C"}:C"\to X$
moves in a family of dimension at most
$f|_{C"}:C"\to X$
moves in a family of dimension at most
and
![]() $C'$
, which is obtained from
$C'$
, which is obtained from
![]() $C"$
by attaching t free curves of degree
$C"$
by attaching t free curves of degree
![]() $e_i$
, moves in a family of dimension at most
$e_i$
, moves in a family of dimension at most
 $$ \begin{align*}e^{\prime\prime}(n+1-d) + (n-1)(1-g) + A + \sum_{i=1}^t (e_i(n+1-d)-1).\end{align*} $$
$$ \begin{align*}e^{\prime\prime}(n+1-d) + (n-1)(1-g) + A + \sum_{i=1}^t (e_i(n+1-d)-1).\end{align*} $$
Because
![]() $C'$
also passes through m general points, we also have
$C'$
also passes through m general points, we also have
 $$ \begin{align*}e^{\prime\prime}(n+1-d) + (n-1)(1-g) + A + \sum_{i=1}^t (e_i(n+1-d)-1) \geq m(n-1).\end{align*} $$
$$ \begin{align*}e^{\prime\prime}(n+1-d) + (n-1)(1-g) + A + \sum_{i=1}^t (e_i(n+1-d)-1) \geq m(n-1).\end{align*} $$
Since
![]() $m(n-1)= e(n+1-d)+(n-1)(1-g)$
and
$m(n-1)= e(n+1-d)+(n-1)(1-g)$
and
![]() $e \geq e^{\prime \prime } +\sum _{i=1}^t e_i$
, we get
$e \geq e^{\prime \prime } +\sum _{i=1}^t e_i$
, we get
![]() $t \leq A$
. Therefore, for large enough m, we have
$t \leq A$
. Therefore, for large enough m, we have
![]() $m-t \geq g+1$
. We conclude from [Reference Lian and PandharipandeLP23, Proposition 13 and Proposition 14] that
$m-t \geq g+1$
. We conclude from [Reference Lian and PandharipandeLP23, Proposition 13 and Proposition 14] that
![]() $h^1(C,f^*T_X|_C)=0$
. In particular,
$h^1(C,f^*T_X|_C)=0$
. In particular,
![]() $f|_{C}:C\to X$
moves in a family of the expected dimension.
$f|_{C}:C\to X$
moves in a family of the expected dimension.
Now, by [Reference Riedl and YangRY19], the space of rational curves passing through any fixed point of X has the expected dimension, and therefore the space of trees of rational curves passing through any fixed point of X has the expected dimension. As
![]() $f|_{C}:C\to X$
also moves in a family of the expected dimension, the same is true of f. By assumption, the domain of f is reducible, so f moves in a family of dimension strictly less than
$f|_{C}:C\to X$
also moves in a family of the expected dimension, the same is true of f. By assumption, the domain of f is reducible, so f moves in a family of dimension strictly less than
![]() $e(n+1-d)+(n-1)(1-g)=m(n-1)$
, which therefore cannot dominate
$e(n+1-d)+(n-1)(1-g)=m(n-1)$
, which therefore cannot dominate
![]() $X^{\times m}$
. This completes the proof.
$X^{\times m}$
. This completes the proof.
We still need to verify the
![]() $h^{1}$
condition used in Lemma 5.4. We first need a lemma.
$h^{1}$
condition used in Lemma 5.4. We first need a lemma.
Lemma 5.5. Let
![]() $m\ge 3$
be an integer. Let
$m\ge 3$
be an integer. Let
![]() $X\subset \mathbb {P}^n$
be a smooth hypersurface of degree
$X\subset \mathbb {P}^n$
be a smooth hypersurface of degree
![]() $d \leq (n+3)/3$
, and let
$d \leq (n+3)/3$
, and let
![]() $p_1, \dots , p_m$
in X be general points. Let
$p_1, \dots , p_m$
in X be general points. Let
![]() $(B,q_1,\ldots ,q_m)\in \overline {M}_{0,m}$
be the unique point of
$(B,q_1,\ldots ,q_m)\in \overline {M}_{0,m}$
be the unique point of
![]() $\overline {M}_{0,m}$
if
$\overline {M}_{0,m}$
if
![]() $m=3$
and the pointed stable curve depicted in Figure 6 if
$m=3$
and the pointed stable curve depicted in Figure 6 if
![]() $m \geq 4$
. So if
$m \geq 4$
. So if
![]() $m \geq 4$
, then B is given by a chain of smooth rational curves
$m \geq 4$
, then B is given by a chain of smooth rational curves
![]() $B_1\cup \cdots \cup B_{m-2}$
with
$B_1\cup \cdots \cup B_{m-2}$
with
![]() $q_i\in B_{i-1}$
for
$q_i\in B_{i-1}$
for
![]() $i=2,\ldots ,m-1$
and additionally
$i=2,\ldots ,m-1$
and additionally
![]() $q_1\in B_1$
and
$q_1\in B_1$
and
![]() $q_m\in B_{m-2}$
. Assume that there exists an m-pointed stable map
$q_m\in B_{m-2}$
. Assume that there exists an m-pointed stable map
![]() $f:\widetilde {B}\to X$
with
$f:\widetilde {B}\to X$
with
![]() $f(\widetilde {q_i})=p_i$
for
$f(\widetilde {q_i})=p_i$
for
![]() $i=1,2,\ldots ,m$
such that the stable contraction of the domain
$i=1,2,\ldots ,m$
such that the stable contraction of the domain
![]() $(\widetilde {B},\widetilde {q_1},\ldots ,\widetilde {q_m})$
is equal to
$(\widetilde {B},\widetilde {q_1},\ldots ,\widetilde {q_m})$
is equal to
![]() $(B,q_1,\ldots ,q_m)$
.
$(B,q_1,\ldots ,q_m)$
.

Figure 6 The curve
![]() $B=B_1\cup \cdots B_{m-2}$
.
$B=B_1\cup \cdots B_{m-2}$
.
Then,
![]() $e(n+1-d)-(m-1)(n-1) \geq 0$
and if
$e(n+1-d)-(m-1)(n-1) \geq 0$
and if
![]() $e(n+1-d)-(m-1)(n-1) =0$
, then
$e(n+1-d)-(m-1)(n-1) =0$
, then
![]() $\widetilde {B}=B$
.
$\widetilde {B}=B$
.
Proof. Let
![]() $c:\widetilde {B}\to B$
be the stabilization map. If
$c:\widetilde {B}\to B$
be the stabilization map. If
![]() $m \geq 4$
, then we abusively denote by
$m \geq 4$
, then we abusively denote by
![]() $B_i$
the unique component of
$B_i$
the unique component of
![]() $\widetilde {B}$
mapping isomorphically to
$\widetilde {B}$
mapping isomorphically to
![]() $B_i\subset B$
. For
$B_i\subset B$
. For
![]() $i=1,2,\ldots ,m-3$
, let
$i=1,2,\ldots ,m-3$
, let
![]() $B_{i,i+1}\subset \widetilde {B}$
be the unique chain of rational curves connecting
$B_{i,i+1}\subset \widetilde {B}$
be the unique chain of rational curves connecting
![]() $B_i$
to
$B_i$
to
![]() $B_{i+1}$
(but not containing either component). Note that
$B_{i+1}$
(but not containing either component). Note that
![]() $B_{i,i+1}$
may be (and in fact, in the end, will be) empty. For
$B_{i,i+1}$
may be (and in fact, in the end, will be) empty. For
![]() $i=1,2,\ldots ,m-3$
, let
$i=1,2,\ldots ,m-3$
, let
![]() $S_i=B_i\cup B_{i,i+1}$
, and let
$S_i=B_i\cup B_{i,i+1}$
, and let
![]() $S_{m-2}=B_{m-2}$
. Let
$S_{m-2}=B_{m-2}$
. Let
![]() $\widetilde {B}_s\subset \widetilde {B}$
be the union of all of the
$\widetilde {B}_s\subset \widetilde {B}$
be the union of all of the
![]() $S_i$
. A piece of the curve
$S_i$
. A piece of the curve
![]() $\widetilde {B}$
is depicted in Figure 7.
$\widetilde {B}$
is depicted in Figure 7.

Figure 7 A piece of the curve
![]() $\widetilde {B}$
. Here, the subcurve
$\widetilde {B}$
. Here, the subcurve
![]() $B_{i,i+1}$
is given by the union of the four components connecting
$B_{i,i+1}$
is given by the union of the four components connecting
![]() $B_i$
to
$B_i$
to
![]() $B_{i+1}$
, and
$B_{i+1}$
, and
![]() $S_i$
is the chain of five curves
$S_i$
is the chain of five curves
![]() $B_i\cup B_{i,i+1}$
. The bold components are part of the spine
$B_i\cup B_{i,i+1}$
. The bold components are part of the spine
![]() $\widetilde {B_s}$
, whereas the gray components are among the trees T.
$\widetilde {B_s}$
, whereas the gray components are among the trees T.
Note that
![]() $\widetilde {B}_s\subset \widetilde {B}$
is itself a chain of rational curves, and
$\widetilde {B}_s\subset \widetilde {B}$
is itself a chain of rational curves, and
![]() $\widetilde {B}$
is obtained from
$\widetilde {B}$
is obtained from
![]() $\widetilde {B}_s$
by attaching pairwise disjoint trees of rational curves at smooth points. Let T be such a rational tree. The stability of f shows that T cannot be contracted by f.
$\widetilde {B}_s$
by attaching pairwise disjoint trees of rational curves at smooth points. Let T be such a rational tree. The stability of f shows that T cannot be contracted by f.
Let
![]() $\widetilde {B}_i$
be the union of
$\widetilde {B}_i$
be the union of
![]() $S_i$
and all of the rational trees T attached to
$S_i$
and all of the rational trees T attached to
![]() $S_i$
. Thus,
$S_i$
. Thus,
![]() $\widetilde {B}$
is the union of all
$\widetilde {B}$
is the union of all
![]() $\widetilde {B}_i$
, for
$\widetilde {B}_i$
, for
![]() $i=1,2,\ldots ,m-2$
, and every component of
$i=1,2,\ldots ,m-2$
, and every component of
![]() $\widetilde {B}$
belongs to exactly one
$\widetilde {B}$
belongs to exactly one
![]() $\widetilde {B}_i$
.
$\widetilde {B}_i$
.
We now proceed to the proof of the Lemma. We may assume that
![]() $e(n+1-d) \leq (m-1)(n-1)$
; we argue by induction on m that equality must hold (and the resulting curve has the claimed form). If
$e(n+1-d) \leq (m-1)(n-1)$
; we argue by induction on m that equality must hold (and the resulting curve has the claimed form). If
![]() $m=3$
, then let
$m=3$
, then let
![]() $\widetilde {B}_s$
be the unique component of
$\widetilde {B}_s$
be the unique component of
![]() $\widetilde {B}$
mapping isomorphically to B. Then
$\widetilde {B}$
mapping isomorphically to B. Then
![]() $e\le \frac {2(n-1)}{n+1-d}$
, and since
$e\le \frac {2(n-1)}{n+1-d}$
, and since
![]() $d \leq (n+3)/3$
, we have
$d \leq (n+3)/3$
, we have
![]() $e\le 2$
. So we have the following cases:
$e\le 2$
. So we have the following cases:
-
1.
 $\deg (\widetilde {B}_s)=2$
, in which case
$\deg (\widetilde {B}_s)=2$
, in which case
 $\widetilde {B}$
must be irreducible,
$\widetilde {B}$
must be irreducible, -
2.
 $\deg (\widetilde {B}_s)=1$
, in which case
$\deg (\widetilde {B}_s)=1$
, in which case
 $\widetilde {B}_s$
must map to a line between two of
$\widetilde {B}_s$
must map to a line between two of
 $p_1,p_2,p_3$
, and a second component
$p_1,p_2,p_3$
, and a second component
 $T\subset \widetilde {B}$
must map to a line through the third point, or
$T\subset \widetilde {B}$
must map to a line through the third point, or -
3.
 $\deg (\widetilde {B}_s)=0$
, in which case
$\deg (\widetilde {B}_s)=0$
, in which case
 $\widetilde {B}_s$
must be contracted to one of
$\widetilde {B}_s$
must be contracted to one of
 $p_1,p_2,p_3$
, and two other components must be attached to
$p_1,p_2,p_3$
, and two other components must be attached to
 $\widetilde {B}_s$
at the other two points, mapping isomorphically to lines on X.
$\widetilde {B}_s$
at the other two points, mapping isomorphically to lines on X.
In the first case,
![]() $f:\widetilde {B}\to X$
is an irreducible free conic, thus moving in a family of the expected dimension, and such an f passes through three general points only when
$f:\widetilde {B}\to X$
is an irreducible free conic, thus moving in a family of the expected dimension, and such an f passes through three general points only when
![]() $e(n+1-d)=(m-1)(n-1)$
. (Here, we get simply
$e(n+1-d)=(m-1)(n-1)$
. (Here, we get simply
![]() $d=2$
, that is, X is a quadric.) In the second case, f is a chain of two free lines, which moves (as a pointed stable map) in a family of the expected dimension of
$d=2$
, that is, X is a quadric.) In the second case, f is a chain of two free lines, which moves (as a pointed stable map) in a family of the expected dimension of
![]() $e(n+1-d)+(n-1)-1< m(n-1)$
, so f cannot pass through
$e(n+1-d)+(n-1)-1< m(n-1)$
, so f cannot pass through
![]() $m=3$
general points. The third case is similarly impossible. This establishes the base case.
$m=3$
general points. The third case is similarly impossible. This establishes the base case.
Suppose now that the Lemma holds for every
![]() $m'<m$
. We use the induction hypotheses and the assumption
$m'<m$
. We use the induction hypotheses and the assumption
![]() $d\leq (n+3)/3$
to show that
$d\leq (n+3)/3$
to show that
![]() $\widetilde {B}$
is a chain of lines and free conics to which some free lines are attached. Fix an index i, and let
$\widetilde {B}$
is a chain of lines and free conics to which some free lines are attached. Fix an index i, and let
![]() $\widetilde {B}'=\bigcup _{j<i}\widetilde {B_j}$
and
$\widetilde {B}'=\bigcup _{j<i}\widetilde {B_j}$
and
![]() $\widetilde {B}^{\prime \prime }=\bigcup _{j>i}\widetilde {B_j}$
. Note that
$\widetilde {B}^{\prime \prime }=\bigcup _{j>i}\widetilde {B_j}$
. Note that
![]() $\widetilde {B}'$
or
$\widetilde {B}'$
or
![]() $\widetilde {B}^{\prime \prime }$
is empty if
$\widetilde {B}^{\prime \prime }$
is empty if
![]() $i=1$
or
$i=1$
or
![]() $i=m-2$
, respectively. Let
$i=m-2$
, respectively. Let
![]() $e',e^{\prime \prime }$
be the total degree of f restricted to
$e',e^{\prime \prime }$
be the total degree of f restricted to
![]() $\widetilde {B}',\widetilde {B}^{\prime \prime }$
, respectively, and let
$\widetilde {B}',\widetilde {B}^{\prime \prime }$
, respectively, and let
![]() $e_i$
be the degree upon restriction to
$e_i$
be the degree upon restriction to
![]() $\widetilde {B_i}$
.
$\widetilde {B_i}$
.
Let
![]() $a' = e'(n+1-d)-(i-1)(n-1)$
and
$a' = e'(n+1-d)-(i-1)(n-1)$
and
![]() $a^{\prime \prime } = e^{\prime \prime }(n+1-d)-((m-i-1)-1)(n-1)$
. If
$a^{\prime \prime } = e^{\prime \prime }(n+1-d)-((m-i-1)-1)(n-1)$
. If
![]() $3 \leq i \leq m-2$
, then by our induction hypothesis
$3 \leq i \leq m-2$
, then by our induction hypothesis
![]() $a' \geq 0$
. If
$a' \geq 0$
. If
![]() $i=2$
, then either
$i=2$
, then either
![]() $d=1$
, or
$d=1$
, or
![]() $d \geq 2$
and there is no line through two general points of X, so
$d \geq 2$
and there is no line through two general points of X, so
![]() $e' \geq 2$
. So in all cases
$e' \geq 2$
. So in all cases
![]() $a' \geq 0$
. Similarly,
$a' \geq 0$
. Similarly,
![]() $a^{\prime \prime } \geq 0$
. Because
$a^{\prime \prime } \geq 0$
. Because
![]() $e=e'+e^{\prime \prime }+e_i$
, we have
$e=e'+e^{\prime \prime }+e_i$
, we have
 $$ \begin{align*} a'+a^{\prime\prime} &=e(n+1-d)-(m-1)(n-1) -e_i(n+1-d)+2(n-1) \\ &\leq -e_i(n+1-d)+2(n-1). \end{align*} $$
$$ \begin{align*} a'+a^{\prime\prime} &=e(n+1-d)-(m-1)(n-1) -e_i(n+1-d)+2(n-1) \\ &\leq -e_i(n+1-d)+2(n-1). \end{align*} $$
If
![]() $e_i(n+1-d)>2(n-1),$
we obtain a contradiction. Therefore, we have
$e_i(n+1-d)>2(n-1),$
we obtain a contradiction. Therefore, we have
![]() $e_i \leq \frac {2(n-1)}{n+1-d} <3$
, so
$e_i \leq \frac {2(n-1)}{n+1-d} <3$
, so
![]() $e_i\leq 2$
.
$e_i\leq 2$
.
We now reduce to the case in which every component of
![]() $\widetilde {B}$
that is a leaf (that is, is connected to only one other component of
$\widetilde {B}$
that is a leaf (that is, is connected to only one other component of
![]() $\widetilde {B}$
) contains a marked point. Indeed, if
$\widetilde {B}$
) contains a marked point. Indeed, if
![]() $\widetilde {B}$
contains a leaf without a marked point, then deleting that component, and stabilizing f if necessary, decreases e while leaving m the same. Thus, it suffices to show that the new stable map, of strictly smaller degree, cannot exist.
$\widetilde {B}$
contains a leaf without a marked point, then deleting that component, and stabilizing f if necessary, decreases e while leaving m the same. Thus, it suffices to show that the new stable map, of strictly smaller degree, cannot exist.
In particular, any tree attached to
![]() $\widetilde {B}_s$
must contain a marked point. By construction, this marked point is unique, so in fact, the tree must be a chain, and all components must map to X with positive degree.
$\widetilde {B}_s$
must contain a marked point. By construction, this marked point is unique, so in fact, the tree must be a chain, and all components must map to X with positive degree.
Now, let
![]() $s_i=\deg (S_i)$
and
$s_i=\deg (S_i)$
and
![]() $t_i=\deg (\widetilde {B}_i)-\deg (S_i)$
. Since
$t_i=\deg (\widetilde {B}_i)-\deg (S_i)$
. Since
![]() $e_{i} \leq 2$
, the only possibilities are that:
$e_{i} \leq 2$
, the only possibilities are that:
-
1.
 $t_i=0$
, in which case
$t_i=0$
, in which case
 $s_i\le 2$
,
$s_i\le 2$
, -
2.
 $t_i=1$
, in which case
$t_i=1$
, in which case
 $s_i\le 1$
, or
$s_i\le 1$
, or -
3.
 $t_i=2$
, in which case
$t_i=2$
, in which case
 $s_i=0$
.
$s_i=0$
.
Case (3) is only possible if
![]() $i=1$
or
$i=1$
or
![]() $i=m-2$
. Indeed, if
$i=m-2$
. Indeed, if
![]() $2\le i\le m-3$
, then after contracting
$2\le i\le m-3$
, then after contracting
![]() $S_i$
and deleting the (necessarily unique) tree attached to it, we obtain an instance of this Lemma with e replaced by
$S_i$
and deleting the (necessarily unique) tree attached to it, we obtain an instance of this Lemma with e replaced by
![]() $e-2$
and m replaced by
$e-2$
and m replaced by
![]() $m-1$
. In this case, since
$m-1$
. In this case, since
![]() $d \leq (n+3)/3$
, we have
$d \leq (n+3)/3$
, we have
![]() $(e-2)(n+1-d)-(m-2)(n-1) <0$
, so f cannot exist by the inductive hypothesis. On the other hand, if
$(e-2)(n+1-d)-(m-2)(n-1) <0$
, so f cannot exist by the inductive hypothesis. On the other hand, if
![]() $i=1$
or
$i=1$
or
![]() $i=m-2$
, then the same argument and the stability of f force
$i=m-2$
, then the same argument and the stability of f force
![]() $S_i$
to consist of a single contracted component, with two free lines passing through the two points
$S_i$
to consist of a single contracted component, with two free lines passing through the two points
![]() $p_1,p_2$
or
$p_1,p_2$
or
![]() $p_{m-1},p_{m}$
.
$p_{m-1},p_{m}$
.
In case (2), the unique tree attached to
![]() $S_i$
must consist of a single line containing a marked point, so in particular, the line is free. In case (1),
$S_i$
must consist of a single line containing a marked point, so in particular, the line is free. In case (1),
![]() $S_i$
consists of a free irreducible conic or a union of two lines.
$S_i$
consists of a free irreducible conic or a union of two lines.
To conclude,
![]() $\widetilde {B}$
consists of a chain of components of degree 0, 1 or free components of degree 2 (and the contracted components are necessarily stable), with possibly some additional free lines containing marked points
$\widetilde {B}$
consists of a chain of components of degree 0, 1 or free components of degree 2 (and the contracted components are necessarily stable), with possibly some additional free lines containing marked points
![]() $\widetilde {q_i}$
attached to the chain. Note that after contracting the degree
$\widetilde {q_i}$
attached to the chain. Note that after contracting the degree
![]() $0$
components in
$0$
components in
![]() $\widetilde {B}_s$
, we get a chain of lines and free conics, so by Proposition 5.3,
$\widetilde {B}_s$
, we get a chain of lines and free conics, so by Proposition 5.3,
![]() $\widetilde {B}_s$
moves in a family of expected dimension. Since the family of free lines through any point of X has the expected dimension
$\widetilde {B}_s$
moves in a family of expected dimension. Since the family of free lines through any point of X has the expected dimension
![]() $n-d-1$
, it follows that f moves in a family of the expected dimension and can therefore only pass through all of the
$n-d-1$
, it follows that f moves in a family of the expected dimension and can therefore only pass through all of the
![]() $p_i$
if
$p_i$
if
![]() $e(n+1-d)-(m-1)(n-1) =0$
and
$e(n+1-d)-(m-1)(n-1) =0$
and
![]() $\widetilde {B}=B$
.
$\widetilde {B}=B$
.
We first prove the genus
![]() $0$
case of Theorem 5.1 using the previous lemmas. We then build off this case to prove the statement for arbitrary genus.
$0$
case of Theorem 5.1 using the previous lemmas. We then build off this case to prove the statement for arbitrary genus.
Proposition 5.6. Let X be a smooth hypersurface of degree d in
![]() $\mathbb {P}^n$
as in Theorem 5.1. For any integer
$\mathbb {P}^n$
as in Theorem 5.1. For any integer
![]() $a \geq 0$
, there is a constant
$a \geq 0$
, there is a constant
![]() $Q_a$
with the following property: If
$Q_a$
with the following property: If
![]() $e, m$
are such that
$e, m$
are such that
![]() $e(n+1-d)-(m-1)(n-1) \leq a$
, then for a general
$e(n+1-d)-(m-1)(n-1) \leq a$
, then for a general
![]() $(C, p_1, \dots , p_m) \in \overline {M}_{0,m} \times X^{\times m}$
and for every
$(C, p_1, \dots , p_m) \in \overline {M}_{0,m} \times X^{\times m}$
and for every
![]() $(\widetilde {C}, f, \widetilde {q}_1,\dots , \widetilde {q}_m)$
in the fiber of
$(\widetilde {C}, f, \widetilde {q}_1,\dots , \widetilde {q}_m)$
in the fiber of
![]() $\phi $
over
$\phi $
over
![]() $(C,p_1, \dots , p_m)$
, we have
$(C,p_1, \dots , p_m)$
, we have
![]() $h^1(\widetilde {C},f^*T_X) \leq Q_a$
.
$h^1(\widetilde {C},f^*T_X) \leq Q_a$
.
Proof. We prove the statement by induction on a. First, suppose
![]() $a=0$
. If X is general, then the statement follows from the irreducibility of the space of rational curves of any given degree on a general hypersurface of degree
$a=0$
. If X is general, then the statement follows from the irreducibility of the space of rational curves of any given degree on a general hypersurface of degree
![]() $\leq n-2$
in
$\leq n-2$
in
![]() $\mathbb {P}^n$
.
$\mathbb {P}^n$
.
Now, assume
![]() $a=0$
and X is an arbitrary smooth hypersurface of degree
$a=0$
and X is an arbitrary smooth hypersurface of degree
![]() $d \leq (n+3)/3$
in
$d \leq (n+3)/3$
in
![]() $\mathbb {P}^n$
. Then by Proposition 5.3 the spaces of chains of lines and free conics in X have the expected dimension. We show for general
$\mathbb {P}^n$
. Then by Proposition 5.3 the spaces of chains of lines and free conics in X have the expected dimension. We show for general
![]() $[C] \in \overline {M}_{0,m}$
and for general points
$[C] \in \overline {M}_{0,m}$
and for general points
![]() $p_1, \dots , p_m \in X$
, we have
$p_1, \dots , p_m \in X$
, we have
![]() $h^1(\widetilde {C},f^*T_X)=0$
for every
$h^1(\widetilde {C},f^*T_X)=0$
for every
![]() $[f]$
in the fiber of
$[f]$
in the fiber of
![]() $\phi $
over
$\phi $
over
![]() $([C],p_1, \dots , p_m)$
, so
$([C],p_1, \dots , p_m)$
, so
![]() $Q_0=0$
. By upper semicontinuity of
$Q_0=0$
. By upper semicontinuity of
![]() $h^1$
, it is enough to show there exists
$h^1$
, it is enough to show there exists
![]() $(C,p_1, \dots , p_m) \in \overline {M}_{0,m} \times X^{\times m}$
such that
$(C,p_1, \dots , p_m) \in \overline {M}_{0,m} \times X^{\times m}$
such that
![]() $h^1(\widetilde {C},f^*T_X)=0$
for every point
$h^1(\widetilde {C},f^*T_X)=0$
for every point
![]() $[f]$
in the fiber of
$[f]$
in the fiber of
![]() $\phi $
over
$\phi $
over
![]() $(C,p_1, \dots , p_m)$
. Taking C to be the point
$(C,p_1, \dots , p_m)$
. Taking C to be the point
![]() $(B,q_1,\ldots ,q_m)\in \overline {M}_{0,m}$
defined in the statement of Lemma 5.5, the conclusion of the same lemma shows that C has the required property.
$(B,q_1,\ldots ,q_m)\in \overline {M}_{0,m}$
defined in the statement of Lemma 5.5, the conclusion of the same lemma shows that C has the required property.
Next, suppose the statement holds for any integer smaller than a. Then for general C,
![]() $p_1, \dots , p_m$
, we use the same argument as in Lemma 5.5. We define
$p_1, \dots , p_m$
, we use the same argument as in Lemma 5.5. We define
![]() $C_i,C_{i,i+1},S_i,\widetilde {C}_s,\widetilde {C}_i\subset \widetilde {C}$
as in the proof of Lemma 5.5 (where we have replaced all instances of B with C), and for any index i, define
$C_i,C_{i,i+1},S_i,\widetilde {C}_s,\widetilde {C}_i\subset \widetilde {C}$
as in the proof of Lemma 5.5 (where we have replaced all instances of B with C), and for any index i, define
![]() $e', e^{\prime \prime },a', a^{\prime \prime },e_i$
, as before. Then,
$e', e^{\prime \prime },a', a^{\prime \prime },e_i$
, as before. Then,
Thus, if
![]() $e_i \geq 3$
for some i, then since
$e_i \geq 3$
for some i, then since
![]() $a',a^{\prime \prime } \geq 0$
, we have
$a',a^{\prime \prime } \geq 0$
, we have
![]() $a', a^{\prime \prime } <a$
. Also,
$a', a^{\prime \prime } <a$
. Also,
![]() $e_i$
is bounded in terms of
$e_i$
is bounded in terms of
![]() $a, n,d$
(since, for example,
$a, n,d$
(since, for example,
![]() $a-e_i(n+1-d)+2(n-1) \geq 0$
). Thus, there is a constant A which depends only on
$a-e_i(n+1-d)+2(n-1) \geq 0$
). Thus, there is a constant A which depends only on
![]() $a, n,d$
such that the contribution to
$a, n,d$
such that the contribution to
![]() $h^1$
from
$h^1$
from
![]() $\widetilde {C_i}$
is at most A. Therefore,
$\widetilde {C_i}$
is at most A. Therefore,
![]() $h^1(\widetilde {C},f^*T_X)\le A+Q_{a'}+Q_{a"}+2n-2,$
and we are done.
$h^1(\widetilde {C},f^*T_X)\le A+Q_{a'}+Q_{a"}+2n-2,$
and we are done.
So we may assume
![]() $e_i \leq 2$
for every i. As in the proof of Lemma 5.5, we next reduce to the case in which all leaves of
$e_i \leq 2$
for every i. As in the proof of Lemma 5.5, we next reduce to the case in which all leaves of
![]() $\widetilde {C}$
contain a marked point. A leaf without a marked point would need to have degree 1 or 2, and deleting it from
$\widetilde {C}$
contain a marked point. A leaf without a marked point would need to have degree 1 or 2, and deleting it from
![]() $\widetilde {C}$
and stabilizing the resulting stable map gives an instance of the Proposition with a replaced by some
$\widetilde {C}$
and stabilizing the resulting stable map gives an instance of the Proposition with a replaced by some
![]() $a'<a$
. Then,
$a'<a$
. Then,
![]() $h^1(\widetilde {C},f^{*}T_X)\le Q_{a'}+A+(n-1)$
, where A denotes here the maximum value of
$h^1(\widetilde {C},f^{*}T_X)\le Q_{a'}+A+(n-1)$
, where A denotes here the maximum value of
![]() $h^1(f^{*}T_X)$
for a line or conic on X. As this operation can be performed no more than a times, we obtain an upper bound on
$h^1(f^{*}T_X)$
for a line or conic on X. As this operation can be performed no more than a times, we obtain an upper bound on
![]() $h^1(\widetilde {C},f^{*}T_X)$
depending only on a.
$h^1(\widetilde {C},f^{*}T_X)$
depending only on a.
Now, we have the same three cases for the degrees of
![]() $s_i,t_i$
as in Lemma 5.5. As before, if we are in case (3) and there exists a tree of degree at least 2 attached to
$s_i,t_i$
as in Lemma 5.5. As before, if we are in case (3) and there exists a tree of degree at least 2 attached to
![]() $\widetilde {C}_s$
, then deleting it and contracting
$\widetilde {C}_s$
, then deleting it and contracting
![]() $S_i$
yields an instance of the Proposition with a replaced by some
$S_i$
yields an instance of the Proposition with a replaced by some
![]() $a'<a$
. As before,
$a'<a$
. As before,
![]() $h^1(\widetilde {C},f^{*}T_X)$
is bounded above in terms of (the finitely many constants)
$h^1(\widetilde {C},f^{*}T_X)$
is bounded above in terms of (the finitely many constants)
![]() $Q_{a'}$
, n and the maximum value of
$Q_{a'}$
, n and the maximum value of
![]() $h^1(f^{*}T_X)$
for a line or conic on X.
$h^1(f^{*}T_X)$
for a line or conic on X.
Finally, we conclude that otherwise, as in Lemma 5.5, f is given by a chain of lines and free conics, possibly along with free lines attached as tails and contracted components. In particular, f moves in a family of the expected dimension. Note that all conics comprising f are free, as they arise from case (1) of the analysis of Lemma 5.5.
On the other hand, f may contain nonfree lines L, which necessarily do not contain any of the marked points. We claim, however, that there can be at most a such components. Indeed, each additional component with no marked point decreases the expected dimension, hence the actual dimension by
![]() $1$
. By assumption, the expected dimension of the space of maps is a more than the dimension of
$1$
. By assumption, the expected dimension of the space of maps is a more than the dimension of
![]() ${\mathcal M}_{g,m}\times X^{\times m}$
. So if there are more than a nonfree components, the space of maps cannot dominate
${\mathcal M}_{g,m}\times X^{\times m}$
. So if there are more than a nonfree components, the space of maps cannot dominate
![]() ${\mathcal M}_{g,m}\times X^{\times m}$
.
${\mathcal M}_{g,m}\times X^{\times m}$
.
Now, the only nontrivial contributions to
![]() $h^1(\widetilde {C},f^{*}T_X)$
come from such components L, of which there are a bounded number. Note that
$h^1(\widetilde {C},f^{*}T_X)$
come from such components L, of which there are a bounded number. Note that
![]() $h^1(L,T_X|_L)$
is uniformly bounded depending only on X. It follows again that
$h^1(L,T_X|_L)$
is uniformly bounded depending only on X. It follows again that
![]() $h^1(\widetilde {C},f^{*}T_X)$
is bounded uniformly in terms of X and a.
$h^1(\widetilde {C},f^{*}T_X)$
is bounded uniformly in terms of X and a.
Proof of Theorem 5.1 for arbitrary g
It suffices to verify the hypothesis of Lemma 5.4. Assume that no such constant A as in the statement of the Lemma exists. Then, given any integer
![]() $A'$
, there exist integers m and e satisfying
$A'$
, there exist integers m and e satisfying
![]() $e(n+1-d)=(m+g-1)(n-1)$
and with the following property. Let
$e(n+1-d)=(m+g-1)(n-1)$
and with the following property. Let
![]() ${[C]=(C, q_1, \dots , q_m)}$
be a point of
${[C]=(C, q_1, \dots , q_m)}$
be a point of
![]() $\overline {\mathcal {M}}_{g,m}$
given by a union of a general pointed curve
$\overline {\mathcal {M}}_{g,m}$
given by a union of a general pointed curve
![]() $(C_0,q_1,\ldots ,q_m)\in M_{0,m}$
and a smooth curve
$(C_0,q_1,\ldots ,q_m)\in M_{0,m}$
and a smooth curve
![]() $C_g$
of genus g, attached at a smooth point of
$C_g$
of genus g, attached at a smooth point of
![]() $C_0$
; see Figure 8. Then, there exists
$C_0$
; see Figure 8. Then, there exists
![]() $(\widetilde {C}, f, \widetilde {q}_1, \dots , \widetilde {q}_m)$
in the fiber over
$(\widetilde {C}, f, \widetilde {q}_1, \dots , \widetilde {q}_m)$
in the fiber over
![]() $([C],p_1,\ldots ,p_m)\in \mathcal {M}_{g,m}\times X^{\times m}$
such that
$([C],p_1,\ldots ,p_m)\in \mathcal {M}_{g,m}\times X^{\times m}$
such that
![]() $h^1(\widetilde {C},f^*T_X)>A'$
.
$h^1(\widetilde {C},f^*T_X)>A'$
.

Figure 8 The curve
![]() $C=C_g\cup C_0$
with
$C=C_g\cup C_0$
with
![]() $q_i\in C_0$
.
$q_i\in C_0$
.
Write
![]() $\widetilde {C}=\widetilde {C}'\cup \widetilde {C}^{\prime \prime }$
so that
$\widetilde {C}=\widetilde {C}'\cup \widetilde {C}^{\prime \prime }$
so that
![]() $\widetilde {C}'$
is a tree of rational curves and contains all m marked points, and
$\widetilde {C}'$
is a tree of rational curves and contains all m marked points, and
![]() $\widetilde {C}^{\prime \prime }$
contains
$\widetilde {C}^{\prime \prime }$
contains
![]() $C_g$
, possibly along with additional rational components. Let
$C_g$
, possibly along with additional rational components. Let
![]() $e',e"$
be the total degrees of the restriction of f to
$e',e"$
be the total degrees of the restriction of f to
![]() $\widetilde {C}', \widetilde {C}^{\prime \prime }$
, respectively.
$\widetilde {C}', \widetilde {C}^{\prime \prime }$
, respectively.
Then
so by Proposition 5.6,
![]() $h^1(f^*T_X|_{\widetilde {C}'})$
is bounded by a constant. On the other hand, if
$h^1(f^*T_X|_{\widetilde {C}'})$
is bounded by a constant. On the other hand, if
then
so the case
![]() $g=0$
implies that no such f can exist. Therefore,
$g=0$
implies that no such f can exist. Therefore,
![]() $e"$
is bounded, so
$e"$
is bounded, so
![]() $h^1(f^*T_X|_{\widetilde {C}"})$
is bounded as well.
$h^1(f^*T_X|_{\widetilde {C}"})$
is bounded as well.
On the other hand, we have assumed that
![]() $h^1(\widetilde {C},f^*T_X)>A'$
for some
$h^1(\widetilde {C},f^*T_X)>A'$
for some
![]() $A'$
arbitrarily large, so we have reached a contradiction. The conclusion now follows from Lemma 5.4.
$A'$
arbitrarily large, so we have reached a contradiction. The conclusion now follows from Lemma 5.4.
Remark 5.7. The same induction argument as in the proofs of Lemma 5.5 and Proposition 5.6 shows that when
![]() $d<(n+3)/2$
, we may only consider the case where
$d<(n+3)/2$
, we may only consider the case where
![]() $e_i \leq 3$
for every i. So the statements, and hence the statement of Theorem 1.13, hold for any smooth hypersurface X in this degree range if we know families of certain trees of lines, conics and free cubics on X have the expected dimension. In fact, one can use Bend-and-Break to reduce this statement to a question about families of trees of lines.
$e_i \leq 3$
for every i. So the statements, and hence the statement of Theorem 1.13, hold for any smooth hypersurface X in this degree range if we know families of certain trees of lines, conics and free cubics on X have the expected dimension. In fact, one can use Bend-and-Break to reduce this statement to a question about families of trees of lines.
Acknowledgements
Part of this project has been conducted during the SQuaRE workshop ‘Geometric Manin’s Conjecture in characteristic p’ at the American Institute of Mathematics. The authors would like to thank AIM for the generous support. We thank Felix Janda for his comments and we also thank the referee for detailed comments which improved the exposition of the paper.
Competing interest
The authors have no competing interest to declare.
Funding statement
Roya Beheshti was supported by NSF grant DMS-2101935. Brian Lehmann was supported by Simons Foundation grant award number 851129. Carl Lian was supported by an NSF postdoctoral fellowship, grant DMS-2001976, the MATH+ incubator grant ‘Tevelev degrees’, and an AMS-Simons travel grant. Eric Riedl was supported by NSF CAREER grant DMS-1945944. Sho Tanimoto was partially supported by JST FOREST program grant number JPMJFR212Z, by JSPS KAKENHI Grant-in-Aid (B) 23K25764 and by JSPS Bilateral Joint Research Projects grant number JPJSBP120219935.