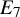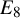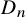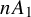1 Introduction
If W is a finite simply laced Weyl group, then it is possible to find a basis of the reflection representation V of W that consists of orthogonal positive roots when W has type
![]() $E_7$
,
$E_7$
,
![]() $E_8$
or
$E_8$
or
![]() $D_n$
for n even. The goal of this paper is to demonstrate that the set
$D_n$
for n even. The goal of this paper is to demonstrate that the set
![]() $X=X(W)$
of such bases has a rich combinatorial structure, both by identifying X with a subset of a Macdonald representation of W and by regarding X as a quasiparabolic set in the sense of Rains and Vazirani [Reference Rains and Vazirani43]. A quasiparabolic set for a Weyl group W is a W-set equipped with an integer-valued height function satisfying two axioms that specify how the action of a reflection changes the height. The axioms generalize properties satisfied by quotients of arbitrary Coxeter groups by their parabolic subgroups that allow one to deform the action of Coxeter group on the quotient to create a corresponding module for the Iwahori–Hecke algebra of the group.
$X=X(W)$
of such bases has a rich combinatorial structure, both by identifying X with a subset of a Macdonald representation of W and by regarding X as a quasiparabolic set in the sense of Rains and Vazirani [Reference Rains and Vazirani43]. A quasiparabolic set for a Weyl group W is a W-set equipped with an integer-valued height function satisfying two axioms that specify how the action of a reflection changes the height. The axioms generalize properties satisfied by quotients of arbitrary Coxeter groups by their parabolic subgroups that allow one to deform the action of Coxeter group on the quotient to create a corresponding module for the Iwahori–Hecke algebra of the group.
Let W be a finite Weyl group with root system
![]() $\Phi $
and Dynkin diagram
$\Phi $
and Dynkin diagram
![]() $\Gamma $
. Let V be the reflection representation of W defined over
$\Gamma $
. Let V be the reflection representation of W defined over
![]() ${\mathbb Q}$
(see Section 2.1), and let
${\mathbb Q}$
(see Section 2.1), and let
![]() $V^*$
be the dual of V over
$V^*$
be the dual of V over
![]() ${\mathbb Q}$
. The space of all rational-valued polynomial functions on V is then the symmetric algebra
${\mathbb Q}$
. The space of all rational-valued polynomial functions on V is then the symmetric algebra
![]() $\textrm {Sym}(V^*)$
, which is a W-module via the contragredient action
$\textrm {Sym}(V^*)$
, which is a W-module via the contragredient action
![]() $(w\cdot \phi )(x) = \phi (w^{-1}(x))$
. Let
$(w\cdot \phi )(x) = \phi (w^{-1}(x))$
. Let
![]() $\Psi $
be a subsystem of
$\Psi $
be a subsystem of
![]() $\Phi $
, meaning that
$\Phi $
, meaning that
![]() $\emptyset \ne \Psi \subset \Phi $
and that
$\emptyset \ne \Psi \subset \Phi $
and that
![]() $\Psi $
is also a root system, and let
$\Psi $
is also a root system, and let
![]() $\Phi ^+$
and
$\Phi ^+$
and
![]() $\Psi ^+$
be the set of positive roots in
$\Psi ^+$
be the set of positive roots in
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
, respectively. Following [Reference Macdonald39], we use the (positive definite) inner product on V to identify V with
$\Psi $
, respectively. Following [Reference Macdonald39], we use the (positive definite) inner product on V to identify V with
![]() $V^*$
, and we define the Macdonald representation
$V^*$
, and we define the Macdonald representation
![]() $j^{\Gamma }_{\Psi }({\mathrm {sgn}}) = j^{\Phi }_{\Psi }({\mathrm {sgn}})$
of W given by
$j^{\Gamma }_{\Psi }({\mathrm {sgn}}) = j^{\Phi }_{\Psi }({\mathrm {sgn}})$
of W given by
![]() $\Psi $
to be the cyclic
$\Psi $
to be the cyclic
![]() ${\mathbb Q} W$
-submodule of
${\mathbb Q} W$
-submodule of
![]() $\textrm {Sym}(V^*)\cong \textrm {Sym}(V)$
generated by
$\textrm {Sym}(V^*)\cong \textrm {Sym}(V)$
generated by
![]() $\pi _\Psi $
, where
$\pi _\Psi $
, where
A short argument shows that the Macdonald representation is an absolutely irreducible W-module.
When W has type
![]() $E_7, E_8$
or
$E_7, E_8$
or
![]() $D_n$
for n even,
$D_n$
for n even,
![]() $\Phi $
contains subsystems of type
$\Phi $
contains subsystems of type
![]() $nA_1$
. The set
$nA_1$
. The set
![]() $\Psi ^+$
for any such subsystem
$\Psi ^+$
for any such subsystem
![]() $\Psi $
consists of n orthogonal positive roots, and we call an element of the form
$\Psi $
consists of n orthogonal positive roots, and we call an element of the form
![]() $w.\pi _\Psi $
(for
$w.\pi _\Psi $
(for
![]() $w \in W$
) an n-root. Thus, an n-root has the form
$w \in W$
) an n-root. Thus, an n-root has the form
![]() $\alpha = \prod _{i = 1}^n \beta _i$
where the elements
$\alpha = \prod _{i = 1}^n \beta _i$
where the elements
![]() $\beta _i$
are orthogonal roots. Conversely, since W acts transitively on the set of maximal sets of orthogonal roots (Lemma 3.2), every product of n orthogonal roots is an n-root. The transitivity of this W-action also implies that any two subsystems of type
$\beta _i$
are orthogonal roots. Conversely, since W acts transitively on the set of maximal sets of orthogonal roots (Lemma 3.2), every product of n orthogonal roots is an n-root. The transitivity of this W-action also implies that any two subsystems of type
![]() $nA_1$
in
$nA_1$
in
![]() $\Phi $
give rise to the same Macdonald representation, which we will thus simply denote as
$\Phi $
give rise to the same Macdonald representation, which we will thus simply denote as
![]() $j^{\Phi }_{nA_1}({\mathrm {sgn}})$
. The representation
$j^{\Phi }_{nA_1}({\mathrm {sgn}})$
. The representation
![]() $j^{\Phi }_{nA_1}({\mathrm {sgn}})$
and the n-roots within it are the central objects of study in this paper, and we summarize their definition below.
$j^{\Phi }_{nA_1}({\mathrm {sgn}})$
and the n-roots within it are the central objects of study in this paper, and we summarize their definition below.
Definition 1.1. Let
![]() $\Phi $
be a root system of type
$\Phi $
be a root system of type
![]() $E_7, E_8$
or
$E_7, E_8$
or
![]() $D_n$
for n even. Let W be the Weyl group of
$D_n$
for n even. Let W be the Weyl group of
![]() $\Phi $
, and let V be the reflection representation of W. We denote the Macdonald representation
$\Phi $
, and let V be the reflection representation of W. We denote the Macdonald representation
![]() $j^{\Phi }_{\Psi }({\mathrm {sgn}})\subset \textrm {Sym}(V^*)\cong \textrm {Sym}(V)$
arising from any subsystem
$j^{\Phi }_{\Psi }({\mathrm {sgn}})\subset \textrm {Sym}(V^*)\cong \textrm {Sym}(V)$
arising from any subsystem
![]() $\Psi $
of type
$\Psi $
of type
![]() $nA_1$
in
$nA_1$
in
![]() $\Phi $
by
$\Phi $
by
![]() $j^{\Phi }_{nA_1}({\mathrm {sgn}})$
. We call each element of the form
$j^{\Phi }_{nA_1}({\mathrm {sgn}})$
. We call each element of the form
![]() $\alpha =\prod _{i=1}^n \beta _i\in j^{\Phi }_{nA_1}({\mathrm {sgn}})$
, where
$\alpha =\prod _{i=1}^n \beta _i\in j^{\Phi }_{nA_1}({\mathrm {sgn}})$
, where
![]() $\beta _1,\cdots ,\beta _n$
are orthogonal roots of
$\beta _1,\cdots ,\beta _n$
are orthogonal roots of
![]() $\Phi $
an n-root of W.
$\Phi $
an n-root of W.
Given an n-root
![]() $\alpha =\prod _{i=1}^n\beta _i$
, the factors
$\alpha =\prod _{i=1}^n\beta _i$
, the factors
![]() $\beta _i$
are unique up to reordering and multiplication by nonzero scalars because they are the irreducible factors of
$\beta _i$
are unique up to reordering and multiplication by nonzero scalars because they are the irreducible factors of
![]() $\alpha $
in the unique factorization domain
$\alpha $
in the unique factorization domain
![]() ${\mathbb Q}[\alpha _1, \alpha _2, \ldots , \alpha _n]$
, where the
${\mathbb Q}[\alpha _1, \alpha _2, \ldots , \alpha _n]$
, where the
![]() $\alpha _i$
correspond to the simple roots of
$\alpha _i$
correspond to the simple roots of
![]() $\Phi $
. We say
$\Phi $
. We say
![]() $\alpha $
is positive if all the factors
$\alpha $
is positive if all the factors
![]() $\beta _i$
may be taken to be positive or, equivalently, if evenly many of the components are negative. If
$\beta _i$
may be taken to be positive or, equivalently, if evenly many of the components are negative. If
![]() $\alpha =\prod _{i=1}^n \beta _i$
is a positive root with all the
$\alpha =\prod _{i=1}^n \beta _i$
is a positive root with all the
![]() $\beta _i$
positive, we call the roots
$\beta _i$
positive, we call the roots
![]() $\beta _i$
the components of
$\beta _i$
the components of
![]() $\alpha $
. An n-root
$\alpha $
. An n-root
![]() $\alpha $
is negative if
$\alpha $
is negative if
![]() $-\alpha $
is positive. It is immediate from the definitions that if
$-\alpha $
is positive. It is immediate from the definitions that if
![]() $\alpha $
is an n-root, then
$\alpha $
is an n-root, then
![]() $-\alpha $
is also an n-root, and that precisely one of
$-\alpha $
is also an n-root, and that precisely one of
![]() $\alpha $
and
$\alpha $
and
![]() $-\alpha $
is positive, similarly to how roots appear in positive-negative pairs in ordinary root systems. If
$-\alpha $
is positive, similarly to how roots appear in positive-negative pairs in ordinary root systems. If
![]() $\alpha $
is either a root or an n-root, we define the absolute value of
$\alpha $
is either a root or an n-root, we define the absolute value of
![]() $\alpha $
, denoted
$\alpha $
, denoted
![]() $\lvert \alpha \rvert $
, to be the positive element in the pair
$\lvert \alpha \rvert $
, to be the positive element in the pair
![]() $\{\alpha ,-\alpha \}$
. (We may view both ordinary roots and n-roots as special cases of k-roots, by which we mean products in
$\{\alpha ,-\alpha \}$
. (We may view both ordinary roots and n-roots as special cases of k-roots, by which we mean products in
![]() $\textrm {Sym}(V^*)$
of k orthogonal roots of W for any fixed integer
$\textrm {Sym}(V^*)$
of k orthogonal roots of W for any fixed integer
![]() $1\le k\le n$
. The notion of k-roots plays an important role in our previous papers [Reference Green and Xu30] and [Reference Green28], and we will occasionally speak of
$1\le k\le n$
. The notion of k-roots plays an important role in our previous papers [Reference Green and Xu30] and [Reference Green28], and we will occasionally speak of
![]() $4$
-roots, even when
$4$
-roots, even when
![]() $n\neq 4$
, in this paper.)
$n\neq 4$
, in this paper.)
The set
![]() $\Phi ^+_n$
of all positive n-roots admits a natural W-action given by
$\Phi ^+_n$
of all positive n-roots admits a natural W-action given by
![]() $w(\alpha )=\lvert w(\alpha ) \rvert $
. Similarly, the set X of sets of n orthogonal roots admits a natural W-action given by
$w(\alpha )=\lvert w(\alpha ) \rvert $
. Similarly, the set X of sets of n orthogonal roots admits a natural W-action given by
![]() $w(\{\beta _1,\cdots ,\beta _n\})=\{\lvert w(\beta _1) \rvert , \cdots , \lvert w(\beta _n) \rvert \}$
. The map sending each set
$w(\{\beta _1,\cdots ,\beta _n\})=\{\lvert w(\beta _1) \rvert , \cdots , \lvert w(\beta _n) \rvert \}$
. The map sending each set
![]() $\{\beta _1,\cdots ,\beta _n\}\in X$
to the product
$\{\beta _1,\cdots ,\beta _n\}\in X$
to the product
![]() $\prod _{i=1}^n \beta _i\in \Phi ^+_n$
respects these two W-actions, and we use it to identify X with
$\prod _{i=1}^n \beta _i\in \Phi ^+_n$
respects these two W-actions, and we use it to identify X with
![]() $\Phi ^+_n$
. In other words, we identify each positive n-root with its set of components.
$\Phi ^+_n$
. In other words, we identify each positive n-root with its set of components.
We show that X has the structure of a quasiparabolic set under a suitable height function
![]() $\lambda $
(Theorem 4.5). As we explain in sections 3 and 4, to understand this structure, it is useful to consider quadruples
$\lambda $
(Theorem 4.5). As we explain in sections 3 and 4, to understand this structure, it is useful to consider quadruples
![]() $Q = \{\beta _1, \beta _2, \beta _3, \beta _4\}$
of four orthogonal roots with the property that
$Q = \{\beta _1, \beta _2, \beta _3, \beta _4\}$
of four orthogonal roots with the property that
![]() $(\beta _1 + \beta _2 + \beta _3 + \beta _4)/2$
is also a root. We call such quadruples coplanar quadruples and show that they fall into three distinct types, called crossings, nestings and alignments. The height function
$(\beta _1 + \beta _2 + \beta _3 + \beta _4)/2$
is also a root. We call such quadruples coplanar quadruples and show that they fall into three distinct types, called crossings, nestings and alignments. The height function
![]() $\lambda $
is given by
$\lambda $
is given by
![]() $\lambda (\gamma )=C(\gamma )+2N(\gamma )$
, where
$\lambda (\gamma )=C(\gamma )+2N(\gamma )$
, where
![]() $C(\gamma )$
and
$C(\gamma )$
and
![]() $N(\gamma )$
are the numbers of crossings and nestings in
$N(\gamma )$
are the numbers of crossings and nestings in
![]() $\gamma $
, respectively, for each
$\gamma $
, respectively, for each
![]() $\gamma \in X$
. The terms ‘crossing’, ‘nesting’ and ‘alignment’ are motivated by the theory of perfect matchings (Remark 3.11).
$\gamma \in X$
. The terms ‘crossing’, ‘nesting’ and ‘alignment’ are motivated by the theory of perfect matchings (Remark 3.11).
As a quasiparabolic set, the set X is equipped with a partial order
![]() $\le _Q$
, which is the weakest partial order such that
$\le _Q$
, which is the weakest partial order such that
![]() $x\le _Q rx$
whenever r is a reflection such that
$x\le _Q rx$
whenever r is a reflection such that
![]() $\lambda (x)\le \lambda (rx)$
. We use the theory of quasiparabolic sets to prove that X has a unique maximally aligned n-root,
$\lambda (x)\le \lambda (rx)$
. We use the theory of quasiparabolic sets to prove that X has a unique maximally aligned n-root,
![]() $\theta _A$
, and a unique maximally nesting n-root,
$\theta _A$
, and a unique maximally nesting n-root,
![]() $\theta _N$
; these two elements are the unique minimal and maximal element of X with respect to
$\theta _N$
; these two elements are the unique minimal and maximal element of X with respect to
![]() $\le _Q$
, respectively (Proposition 4.11). The n-roots that avoid alignments, or the alignment-free n-roots, form a quasiparabolic set
$\le _Q$
, respectively (Proposition 4.11). The n-roots that avoid alignments, or the alignment-free n-roots, form a quasiparabolic set
![]() $X_I \subset X$
of a certain maximal parabolic subgroup
$X_I \subset X$
of a certain maximal parabolic subgroup
![]() $W_I$
of W. The corresponding partial order on
$W_I$
of W. The corresponding partial order on
![]() $X_I$
allows us to show that X also has a maximally crossing element,
$X_I$
allows us to show that X also has a maximally crossing element,
![]() $\theta _C$
, and that it is the unique minimal element of
$\theta _C$
, and that it is the unique minimal element of
![]() $X_I$
(Proposition 5.2 (iii)). The set
$X_I$
(Proposition 5.2 (iii)). The set
![]() $X_I$
has a natural bipartite structure, with the n-roots in
$X_I$
has a natural bipartite structure, with the n-roots in
![]() $X_I$
with even levels and those with odd levels partitioning
$X_I$
with even levels and those with odd levels partitioning
![]() $X_I$
into two equal-sized components that are interchanged by every reflection in
$X_I$
into two equal-sized components that are interchanged by every reflection in
![]() $W_I$
(Remark 5.3).
$W_I$
(Remark 5.3).
The alignment-free n-roots in X are one of three families that avoid a particular type of coplanar quadruple, the other two being those that avoid crossings and avoid nestings. Section 5 studies these three families together. We use a version of Bergman’s diamond lemma to show that the noncrossing elements of X form a basis for the Macdonald representation, as do the nonnesting positive n-roots (Theorem 5.5). In addition, the noncrossing basis behaves somewhat like a simple system in a root system (Theorem 5.7) and may be viewed as a canonical basis (Remark 5.8). The nonnesting basis is naturally parametrized by a particular interval
![]() $[1, w_N]$
in the weak Bruhat order of W and has the structure of a distributive lattice (Theorem 5.13). The element
$[1, w_N]$
in the weak Bruhat order of W and has the structure of a distributive lattice (Theorem 5.13). The element
![]() $w_N$
, which we call the nonnesting element of W, is the unique shortest element taking the maximally crossing n-root
$w_N$
, which we call the nonnesting element of W, is the unique shortest element taking the maximally crossing n-root
![]() $\theta _C$
to the maximally aligned element
$\theta _C$
to the maximally aligned element
![]() $\theta _A$
. We note that the noncrossing basis is essentially the same as a basis that appears in the work of Fan [Reference Fan23, Section 6] and others, although the realization of the basis as polynomials in roots seems to be new.
$\theta _A$
. We note that the noncrossing basis is essentially the same as a basis that appears in the work of Fan [Reference Fan23, Section 6] and others, although the realization of the basis as polynomials in roots seems to be new.
We say that two positive n-roots are sum equivalent or
![]() $\sigma $
-equivalent if their sets of components have the same sum. We show that the
$\sigma $
-equivalent if their sets of components have the same sum. We show that the
![]() $\sigma $
-equivalence classes are in canonical bijection with the nonnesting and the noncrossing elements of X in the following way: each
$\sigma $
-equivalence classes are in canonical bijection with the nonnesting and the noncrossing elements of X in the following way: each
![]() $\sigma $
-equivalence class is an interval
$\sigma $
-equivalence class is an interval
![]() $[\beta _1,\beta _2]_Q=\{\gamma \in X:\beta _1\le _Q \gamma \le _Q \beta _2\}$
in the quasiparabolic order
$[\beta _1,\beta _2]_Q=\{\gamma \in X:\beta _1\le _Q \gamma \le _Q \beta _2\}$
in the quasiparabolic order
![]() $\le _Q$
, where the minimal element
$\le _Q$
, where the minimal element
![]() $\beta _1$
and maximal element
$\beta _1$
and maximal element
![]() $\beta _2$
are the unique nonnesting and noncrossing n-roots in the class, respectively. The alignment-free elements in X form a single
$\beta _2$
are the unique nonnesting and noncrossing n-roots in the class, respectively. The alignment-free elements in X form a single
![]() $\sigma $
-equivalence class that is maximal with respect to a natural order (Proposition 5.15). Any set of
$\sigma $
-equivalence class that is maximal with respect to a natural order (Proposition 5.15). Any set of
![]() $\sigma $
-equivalence class representatives forms a basis for the Macdonald representation, and the change of basis matrix between any two such bases, such as the one between the nonnesting and noncrossing basis, is always unitriangular with integer entries once the bases are suitably ordered (Theorem 5.16).
$\sigma $
-equivalence class representatives forms a basis for the Macdonald representation, and the change of basis matrix between any two such bases, such as the one between the nonnesting and noncrossing basis, is always unitriangular with integer entries once the bases are suitably ordered (Theorem 5.16).
As we explain in Section 7.3, the feature-avoiding n-roots and
![]() $\sigma $
-equivalence classes in the set X can all be characterized abstractly using the quasiparabolic structure of X, without using the combinatorics of sets of roots. This raises the possibility of extending the notions of alignment-free, noncrossing and nonnesting elements to more general quasiparabolic sets.
$\sigma $
-equivalence classes in the set X can all be characterized abstractly using the quasiparabolic structure of X, without using the combinatorics of sets of roots. This raises the possibility of extending the notions of alignment-free, noncrossing and nonnesting elements to more general quasiparabolic sets.
The theory developed in this paper has various natural connections to many previous works. In type
![]() $D_n$
for an even integer
$D_n$
for an even integer
![]() $n=2k$
, the n-roots correspond naturally to perfect matchings of the set
$n=2k$
, the n-roots correspond naturally to perfect matchings of the set
![]() $[n]=\{1,2,\dots ,n\}$
, and the crossings, nestings and alignments in n-roots recover the corresponding notions in the theory of matchings. Besides matchings, the quasiparabolic set X can be identified with the set of fixed-point free involutions in
$[n]=\{1,2,\dots ,n\}$
, and the crossings, nestings and alignments in n-roots recover the corresponding notions in the theory of matchings. Besides matchings, the quasiparabolic set X can be identified with the set of fixed-point free involutions in
![]() $S_n$
, which is one of the original motivating examples of a quasiparabolic set [Reference Rains and Vazirani43, Section 4]. The level function
$S_n$
, which is one of the original motivating examples of a quasiparabolic set [Reference Rains and Vazirani43, Section 4]. The level function
![]() $\lambda =C+2N$
appears as a useful statistic on matchings in [Reference Simion and Stanton52, Reference Díaz and Pariguan20, Reference Cheon and Jung15] and has a natural interpretation in the context of combinatorial game theory [Reference Irie36]; see Section 6.1.
$\lambda =C+2N$
appears as a useful statistic on matchings in [Reference Simion and Stanton52, Reference Díaz and Pariguan20, Reference Cheon and Jung15] and has a natural interpretation in the context of combinatorial game theory [Reference Irie36]; see Section 6.1.
The Macdonald representation
![]() $j^{\Phi }_{nA_1}({\mathrm {sgn}})$
in type
$j^{\Phi }_{nA_1}({\mathrm {sgn}})$
in type
![]() $D_n$
for n even recovers a Specht module in a very natural way: the action of the Weyl group W factors through an obvious sign-forgetting map (Equation (2.2)) to induce an
$D_n$
for n even recovers a Specht module in a very natural way: the action of the Weyl group W factors through an obvious sign-forgetting map (Equation (2.2)) to induce an
![]() $S_n$
-module structure on the Macdonald representation for the symmetric group
$S_n$
-module structure on the Macdonald representation for the symmetric group
![]() $S_n$
, and the resulting module is isomorphic to a realization of the Specht module corresponding to the two-row partition
$S_n$
, and the resulting module is isomorphic to a realization of the Specht module corresponding to the two-row partition
![]() $(k,k)$
due to Rhoades [Reference Rhoades47] (Proposition 6.2). The noncrossing bases and nonnesting bases have been studied extensively as the web basis and the Specht basis, respectively, of the Specht module [Reference Russell and Tymoczko48, Reference Im and Zhu35, Reference Hwang, Jang and Oh34, Reference Heard and Kujawa32]; see Section 6.1.
$(k,k)$
due to Rhoades [Reference Rhoades47] (Proposition 6.2). The noncrossing bases and nonnesting bases have been studied extensively as the web basis and the Specht basis, respectively, of the Specht module [Reference Russell and Tymoczko48, Reference Im and Zhu35, Reference Hwang, Jang and Oh34, Reference Heard and Kujawa32]; see Section 6.1.
In type
![]() $E_7$
, the Macdonald representation contains 135 positive 7-roots and has degree 15 [Reference Colombo, van Geemen, Looijenga and Honor19, Proposition 4.12]. This representation has a long history, going back the work of Coble in 1916 [Reference Coble16, (65)] on the Göpel variety. There are also applications of
$E_7$
, the Macdonald representation contains 135 positive 7-roots and has degree 15 [Reference Colombo, van Geemen, Looijenga and Honor19, Proposition 4.12]. This representation has a long history, going back the work of Coble in 1916 [Reference Coble16, (65)] on the Göpel variety. There are also applications of
![]() $7$
-roots to quantum information theory and supergravity [Reference Cerchiai and van Geemen12, Section IV G], [Reference Duff and Ferrara22]. In this case, the elements of the quasiparabolic set
$7$
-roots to quantum information theory and supergravity [Reference Cerchiai and van Geemen12, Section IV G], [Reference Duff and Ferrara22]. In this case, the elements of the quasiparabolic set
![]() $X_I$
are in canonical bijection with the 30 distinct labellings of the Fano plane, and the maximal and minimal elements are given by
$X_I$
are in canonical bijection with the 30 distinct labellings of the Fano plane, and the maximal and minimal elements are given by
![]() $\{136, 145, 127, 235, 246, 347, 567\}$
and
$\{136, 145, 127, 235, 246, 347, 567\}$
and
![]() $\{123, 145, 246, 257, 347, 356, 167\}$
, respectively (Proposition 6.5).
$\{123, 145, 246, 257, 347, 356, 167\}$
, respectively (Proposition 6.5).
In type
![]() $E_8$
, there are 2025 positive
$E_8$
, there are 2025 positive
![]() $8$
-roots. The bases of orthogonal roots have applications to physics, where they can be used to prove the Kochen–Specker theorem in quantum mechanics [Reference Waegell and Aravind57] (Section 7.2). The Macdonald representation in this case has degree
$8$
-roots. The bases of orthogonal roots have applications to physics, where they can be used to prove the Kochen–Specker theorem in quantum mechanics [Reference Waegell and Aravind57] (Section 7.2). The Macdonald representation in this case has degree
![]() $50$
but seems not to have been studied much before. The quasiparabolic set
$50$
but seems not to have been studied much before. The quasiparabolic set
![]() $X_I$
in this case is a bipartite structure with 240 elements. As we explain in Section 6.3, either partite component can be used to define a graph that has an interesting relationship with two strongly regular graphs studied recently by Schmidt [Reference Schmidt51] (Remark 6.13). Those two graphs each have 120 vertices, and they have the remarkable property of being quantum isomorphic (in the sense of [Reference Atserias, Mančinska, Roberson, Šámal, Severini and Varvitsiotis3]) but not isomorphic.
$X_I$
in this case is a bipartite structure with 240 elements. As we explain in Section 6.3, either partite component can be used to define a graph that has an interesting relationship with two strongly regular graphs studied recently by Schmidt [Reference Schmidt51] (Remark 6.13). Those two graphs each have 120 vertices, and they have the remarkable property of being quantum isomorphic (in the sense of [Reference Atserias, Mančinska, Roberson, Šámal, Severini and Varvitsiotis3]) but not isomorphic.
The properties of n-roots summarized in the last three paragraphs are explained in more detail in Section 6. It is worth noting that while these properties are type-specific, we have attempted to develop the theory of n-roots in a type-independent way in the other parts of the paper in general. In particular, we give a uniform proof for the fact that the positive n-roots form a quasiparabolic set in types
![]() $E_7, E_8,$
and
$E_7, E_8,$
and
![]() $D_{2k}$
(Theorem 4.5). While it is possible to verify the theorem for types
$D_{2k}$
(Theorem 4.5). While it is possible to verify the theorem for types
![]() $E_7$
and
$E_7$
and
![]() $E_8$
using direct computation (which we did, using the software SageMath [Reference Developers49]) and then separately deduce the theorem for type
$E_8$
using direct computation (which we did, using the software SageMath [Reference Developers49]) and then separately deduce the theorem for type
![]() $D_{2k}$
by considering the
$D_{2k}$
by considering the
![]() $S_{2k}$
-action on its fixed-point free involutions, our uniform proof of the theorem relying on Proposition 4.7 has the advantage of being more conceptual and revealing more details about the action of reflections on n-roots. Some of these details will be further used in a forthcoming paper [Reference Green and Xu31], where we will generalize aspects of this paper and study quasiparabolic sets arising from k-roots for more general values of k.
$S_{2k}$
-action on its fixed-point free involutions, our uniform proof of the theorem relying on Proposition 4.7 has the advantage of being more conceptual and revealing more details about the action of reflections on n-roots. Some of these details will be further used in a forthcoming paper [Reference Green and Xu31], where we will generalize aspects of this paper and study quasiparabolic sets arising from k-roots for more general values of k.
The rest of the paper is organized as follows. We recall the basics of root systems in Section 2. Section 3 introduces the key notions of crossings, nestings and alignments in an n-root, and we connect them to the theory of quasiparabolic sets in Section 4. Section 5 studies the alignment-free, noncrossing and nonnesting n-roots. Section 6 discusses the details of n-roots in the types
![]() $D_n$
with n even,
$D_n$
with n even,
![]() $E_7$
and
$E_7$
and
![]() $E_8$
. Section 7 concludes the paper and includes discussions of the Poincaré polynomial of the set X and of orbits of n-roots under the action of Coxeter elements.
$E_8$
. Section 7 concludes the paper and includes discussions of the Poincaré polynomial of the set X and of orbits of n-roots under the action of Coxeter elements.
2 Review of root systems
In this section, we recall the basic properties of simply laced root systems of finite type. We will mostly follow the notation of the first two chapters of [Reference Humphreys33], except in the case of type
![]() $E_7$
, where we follow [Reference Green26, Section 4].
$E_7$
, where we follow [Reference Green26, Section 4].
2.1 Weyl groups, root systems and reflection representations
The root systems in this paper will be irreducible simply laced root systems of finite type, whose Dynkin diagrams are shown in Figure 1. The vertices of the Dynkin diagram
![]() $\Gamma $
index the simple roots
$\Gamma $
index the simple roots
![]() $\Pi = \{\alpha _i : i \in \Gamma \}$
. The root lattice
$\Pi = \{\alpha _i : i \in \Gamma \}$
. The root lattice
![]() ${\mathbb Z}\Pi $
is the free
${\mathbb Z}\Pi $
is the free
![]() ${\mathbb Z}$
-module on
${\mathbb Z}$
-module on
![]() $\Pi $
. We define a
$\Pi $
. We define a
![]() ${\mathbb Z}$
-bilinear form B on
${\mathbb Z}$
-bilinear form B on
![]() ${\mathbb Z}\Pi \times {\mathbb Z}\Pi $
by
${\mathbb Z}\Pi \times {\mathbb Z}\Pi $
by
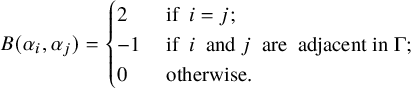
If
![]() $\alpha _i \in \Pi $
, then we define the simple reflection
$\alpha _i \in \Pi $
, then we define the simple reflection
![]() $s_i=s_{\alpha _i}$
to be the
$s_i=s_{\alpha _i}$
to be the
![]() ${\mathbb Z}$
-linear operator
${\mathbb Z}$
-linear operator
![]() ${\mathbb Z}\Pi \rightarrow {\mathbb Z}\Pi $
given by
${\mathbb Z}\Pi \rightarrow {\mathbb Z}\Pi $
given by
The Weyl group
![]() $W = W(\Gamma )$
is the finite group generated by the simple reflections.
$W = W(\Gamma )$
is the finite group generated by the simple reflections.
The root system of W is the set
![]() $\Phi = \{w(\alpha _i) : \alpha _i \in \Pi , w \in W\}$
. Each element of
$\Phi = \{w(\alpha _i) : \alpha _i \in \Pi , w \in W\}$
. Each element of
![]() $\Phi $
is called a root. The group W acts transitively on
$\Phi $
is called a root. The group W acts transitively on
![]() $\Phi $
, and the form B is W-invariant in the sense that
$\Phi $
, and the form B is W-invariant in the sense that
![]() $B(\alpha , \beta ) = B(w(\alpha ), w(\beta ))$
for all
$B(\alpha , \beta ) = B(w(\alpha ), w(\beta ))$
for all
![]() $w \in W$
and all
$w \in W$
and all
![]() $\alpha , \beta \in \Phi $
. We say two roots are
$\alpha , \beta \in \Phi $
. We say two roots are
![]() $\alpha ,\beta \in \Phi $
are orthogonal if
$\alpha ,\beta \in \Phi $
are orthogonal if
![]() $B(\alpha ,\beta )=0$
.
$B(\alpha ,\beta )=0$
.
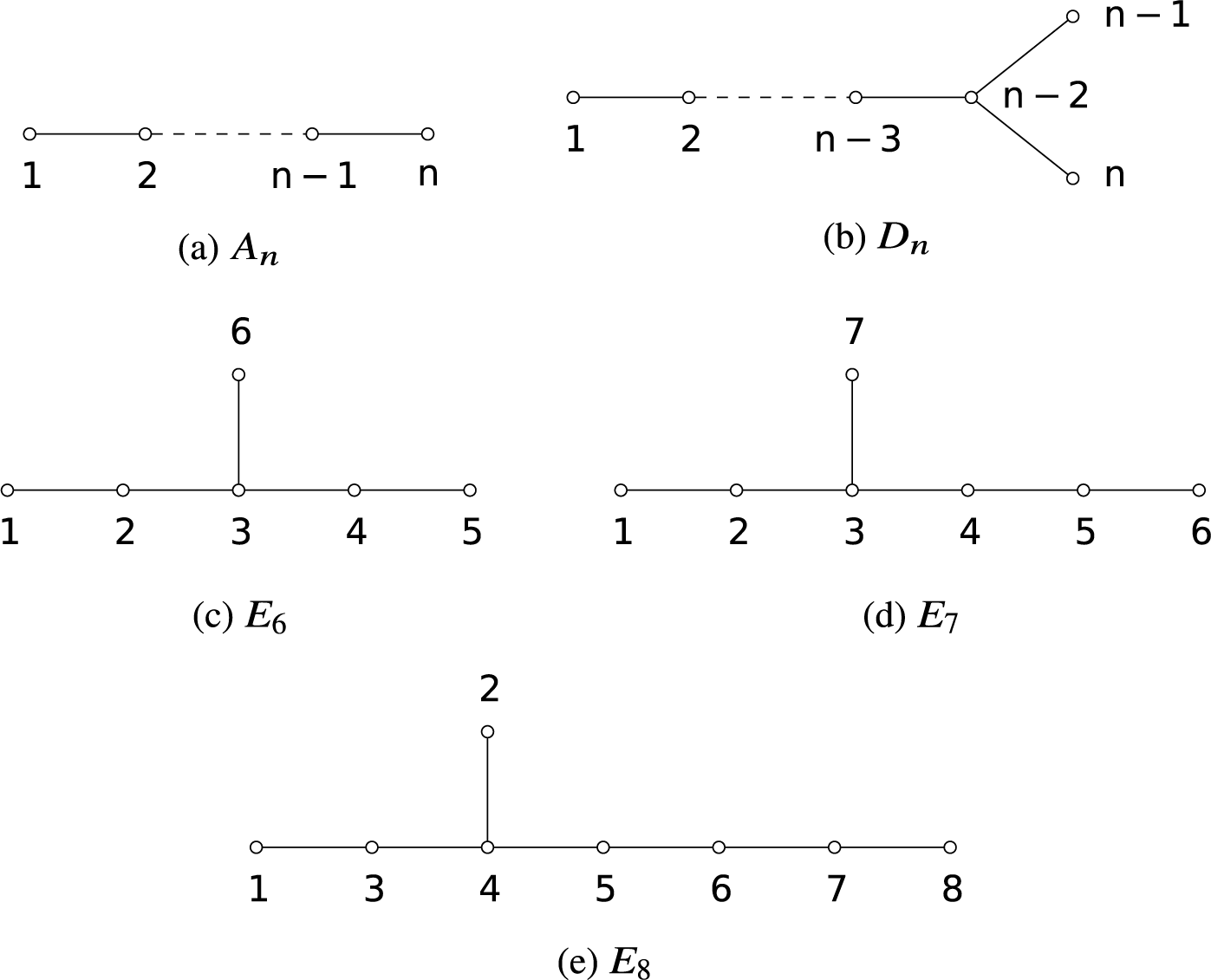
Figure 1 Dynkin diagrams of irreducible simply laced Weyl groups.
Each root
![]() $\alpha \in \Phi $
gives rise to a reflection in W, which is the self-inverse
$\alpha \in \Phi $
gives rise to a reflection in W, which is the self-inverse
![]() ${\mathbb Z}$
-linear operator
${\mathbb Z}$
-linear operator
![]() ${s_\alpha :{\mathbb Z}\Pi \rightarrow {\mathbb Z}\Pi} $
generalizing simple reflections and given by the formula
${s_\alpha :{\mathbb Z}\Pi \rightarrow {\mathbb Z}\Pi} $
generalizing simple reflections and given by the formula
The reflections in W form a single conjugacy class. The
![]() ${\mathbb Q}$
-vector space
${\mathbb Q}$
-vector space
![]() $V := {\mathbb Q} \otimes _{\mathbb Z} {\mathbb Z}\Pi $
affords the reflection representation of W, where each reflection
$V := {\mathbb Q} \otimes _{\mathbb Z} {\mathbb Z}\Pi $
affords the reflection representation of W, where each reflection
![]() $s_\alpha $
acts by Equation (2.1).
$s_\alpha $
acts by Equation (2.1).
A subset
![]() $\Psi $
of
$\Psi $
of
![]() $\Phi $
is called a subsystem if
$\Phi $
is called a subsystem if
![]() $\Psi $
is itself a root system (in the sense of [Reference Humphreys33, Section 1.2]). For each root
$\Psi $
is itself a root system (in the sense of [Reference Humphreys33, Section 1.2]). For each root
![]() $\alpha \in \Phi $
, the set
$\alpha \in \Phi $
, the set
![]() $\Phi _\alpha :=\{\beta \in \Phi :B(\alpha ,\beta )=0\}$
is automatically a subsystem.
$\Phi _\alpha :=\{\beta \in \Phi :B(\alpha ,\beta )=0\}$
is automatically a subsystem.
2.2 Positive and simple systems
A subset
![]() $\Delta $
of a root system
$\Delta $
of a root system
![]() $\Phi $
is called a simple system if
$\Phi $
is called a simple system if
![]() $\Delta $
is a vector space basis for V and every root is a linear combination of
$\Delta $
is a vector space basis for V and every root is a linear combination of
![]() $\Delta $
with coefficients of like sign. Given such a system
$\Delta $
with coefficients of like sign. Given such a system
![]() $\Delta $
, we say a root
$\Delta $
, we say a root
![]() $\alpha = \sum _{i \in \Gamma } c_i \alpha _i$
is positive (with respect to
$\alpha = \sum _{i \in \Gamma } c_i \alpha _i$
is positive (with respect to
![]() $\Delta $
) if
$\Delta $
) if
![]() $c_i\ge 0$
for all i, and we call
$c_i\ge 0$
for all i, and we call
![]() $\alpha $
negative if
$\alpha $
negative if
![]() $c_i\le 0$
for all i. The sets of positive and negative roots are denoted by
$c_i\le 0$
for all i. The sets of positive and negative roots are denoted by
![]() $\Phi _\Delta ^+$
and
$\Phi _\Delta ^+$
and
![]() $\Phi _\Delta ^-$
, and they are setwise negations of each other. For each root
$\Phi _\Delta ^-$
, and they are setwise negations of each other. For each root
![]() $\alpha $
, the integer
$\alpha $
, the integer
![]() $\textrm {ht}(\alpha ) = \sum _{i \in \Gamma } c_i$
is called the height of
$\textrm {ht}(\alpha ) = \sum _{i \in \Gamma } c_i$
is called the height of
![]() $\alpha $
. The set
$\alpha $
. The set
![]() $\{\alpha _i:c_i\neq 0\}$
is called the support of
$\{\alpha _i:c_i\neq 0\}$
is called the support of
![]() $\alpha $
(with respect to
$\alpha $
(with respect to
![]() $\Delta $
).
$\Delta $
).
Each simple system
![]() $\Delta $
also gives rise to a partial order
$\Delta $
also gives rise to a partial order
![]() $\le _\Delta $
on
$\le _\Delta $
on
![]() $\Phi $
, which is defined by the condition that
$\Phi $
, which is defined by the condition that
![]() $\alpha \leq \beta $
if and only if
$\alpha \leq \beta $
if and only if
![]() $\beta - \alpha $
is a nonnegative linear combination of
$\beta - \alpha $
is a nonnegative linear combination of
![]() $\Delta $
. With respect to this partial order,
$\Delta $
. With respect to this partial order,
![]() $\Phi $
has a unique maximal element,
$\Phi $
has a unique maximal element,
![]() $\theta _\Delta $
, called the highest root.
$\theta _\Delta $
, called the highest root.
The set of simple roots
![]() $\Pi $
is an example of a simple system, and the corresponding set of positive roots is an example of a positive system. Recall that each positive system P contains a unique simple system, which is the set
$\Pi $
is an example of a simple system, and the corresponding set of positive roots is an example of a positive system. Recall that each positive system P contains a unique simple system, which is the set
![]() $\Delta _P$
of all elements in P that cannot be expressed as positive linear combinations of other elements of P. The maps
$\Delta _P$
of all elements in P that cannot be expressed as positive linear combinations of other elements of P. The maps
![]() $\Delta \mapsto \Phi _\Delta ^+$
and
$\Delta \mapsto \Phi _\Delta ^+$
and
![]() $P\mapsto \Delta _P$
are mutually inverse bijections between the sets of simple systems and positive systems in
$P\mapsto \Delta _P$
are mutually inverse bijections between the sets of simple systems and positive systems in
![]() $\Phi $
[Reference Humphreys33, Theorem 1.3]. The simple systems of
$\Phi $
[Reference Humphreys33, Theorem 1.3]. The simple systems of
![]() $\Phi $
are conjugate to each other under the action of W, as are the positive systems.
$\Phi $
are conjugate to each other under the action of W, as are the positive systems.
From now on, we choose
![]() $\Pi $
as the default simple system of
$\Pi $
as the default simple system of
![]() $\Phi $
and choose
$\Phi $
and choose
![]() $\Phi ^+_\Pi $
as the default positive system. For each notion defined above relative to a general simple system
$\Phi ^+_\Pi $
as the default positive system. For each notion defined above relative to a general simple system
![]() $\Delta $
, an omission of the subscript in the corresponding notation will indicate that
$\Delta $
, an omission of the subscript in the corresponding notation will indicate that
![]() $\Pi $
is chosen as
$\Pi $
is chosen as
![]() $\Delta $
. For example, the set of positive roots with respect to
$\Delta $
. For example, the set of positive roots with respect to
![]() $\Pi $
will be denoted by
$\Pi $
will be denoted by
![]() $\Phi ^+$
.
$\Phi ^+$
.
For any subsystem
![]() $\Psi $
of
$\Psi $
of
![]() $\Phi $
, the set
$\Phi $
, the set
![]() $\Psi ^+:=\Psi \cap \Phi ^+$
is automatically a positive system of
$\Psi ^+:=\Psi \cap \Phi ^+$
is automatically a positive system of
![]() $\Psi $
. We call
$\Psi $
. We call
![]() $\Psi ^+$
the induced positive system of
$\Psi ^+$
the induced positive system of
![]() $\Psi $
with respect to
$\Psi $
with respect to
![]() $\Phi ^+$
. We call the corresponding simple system of
$\Phi ^+$
. We call the corresponding simple system of
![]() $\Psi $
the induced simple system of
$\Psi $
the induced simple system of
![]() $\Psi $
.
$\Psi $
.
If
![]() $\Psi $
is a subsystem of the form
$\Psi $
is a subsystem of the form
![]() $\Phi _\alpha $
(i.e., if
$\Phi _\alpha $
(i.e., if
![]() $\Psi $
is the subsystem of roots orthogonal to a root
$\Psi $
is the subsystem of roots orthogonal to a root
![]() $\alpha $
), then we denote the induced simple system by
$\alpha $
), then we denote the induced simple system by
![]() $\Pi _\alpha $
. The elements of
$\Pi _\alpha $
. The elements of
![]() $\Pi _\alpha $
are thus the positive roots orthogonal to
$\Pi _\alpha $
are thus the positive roots orthogonal to
![]() $\alpha $
that cannot be expressed as a nonnegative linear combination of other positive roots orthogonal to
$\alpha $
that cannot be expressed as a nonnegative linear combination of other positive roots orthogonal to
![]() $\alpha $
. Note that the elements of
$\alpha $
. Note that the elements of
![]() $\Pi _\alpha $
may not all lie in
$\Pi _\alpha $
may not all lie in
![]() $\Pi $
, but every simple root
$\Pi $
, but every simple root
![]() $\alpha _i\in \Pi $
that lies in
$\alpha _i\in \Pi $
that lies in
![]() $\Psi $
and is orthogonal to
$\Psi $
and is orthogonal to
![]() $\alpha $
will lie in
$\alpha $
will lie in
![]() $\Pi _\alpha $
. We denote the Weyl group corresponding to
$\Pi _\alpha $
. We denote the Weyl group corresponding to
![]() $\Pi _\alpha $
by
$\Pi _\alpha $
by
![]() $W_\alpha $
, so that
$W_\alpha $
, so that
![]() $\Phi _\alpha $
is the root system of
$\Phi _\alpha $
is the root system of
![]() $W_\alpha $
. It is known that
$W_\alpha $
. It is known that
![]() $W_\alpha $
is the stabilizer of
$W_\alpha $
is the stabilizer of
![]() $\alpha $
under the action of W and
$\alpha $
under the action of W and
![]() $W_\alpha $
is a direct product of irreducible simply laced Weyl groups [Reference Brink7, Reference Allcock1]. We will recall the known Dynkin type of the groups
$W_\alpha $
is a direct product of irreducible simply laced Weyl groups [Reference Brink7, Reference Allcock1]. We will recall the known Dynkin type of the groups
![]() $W_\alpha $
in the next subsection.
$W_\alpha $
in the next subsection.
Example 2.1. Let W be the Weyl group of type
![]() $D_5$
and let
$D_5$
and let
![]() $\alpha _2$
be the simple root of W under the labelling used in Figure 1. The induced simple system of
$\alpha _2$
be the simple root of W under the labelling used in Figure 1. The induced simple system of
![]() $\Phi _{\alpha _2}$
is given by the disjoint union
$\Phi _{\alpha _2}$
is given by the disjoint union
where each root in one part of the union is orthogonal to every root in the other part. The Weyl group
![]() $W_{\alpha _2}$
corresponding to
$W_{\alpha _2}$
corresponding to
![]() $\Phi _{\alpha _2}$
is the direct product
$\Phi _{\alpha _2}$
is the direct product
![]() $W(A_1)\times W(A_3)$
of the Weyl groups of types
$W(A_1)\times W(A_3)$
of the Weyl groups of types
![]() $A_1$
and
$A_1$
and
![]() $A_3$
, generated respectively by the sets
$A_3$
, generated respectively by the sets
![]() $\{s_{\beta _1}\}$
and
$\{s_{\beta _1}\}$
and
![]() $\{s_{\beta _2}, s_{\beta _3}, s_{\beta _4}\}$
.
$\{s_{\beta _2}, s_{\beta _3}, s_{\beta _4}\}$
.
2.3 Explicit constructions
We now recall well-known explicit realizations of the root systems of types
![]() $A,D$
and E in coordinate systems. Let
$A,D$
and E in coordinate systems. Let
![]() $\varepsilon _1, \varepsilon _2, \ldots , \varepsilon _n$
be the usual standard basis of the Euclidean space
$\varepsilon _1, \varepsilon _2, \ldots , \varepsilon _n$
be the usual standard basis of the Euclidean space
![]() ${\mathbb R}^n$
. The vectors
${\mathbb R}^n$
. The vectors
![]() $\{\varepsilon _i - \varepsilon _j : 1 \leq i \ne j \leq n\}$
form a root system of type
$\{\varepsilon _i - \varepsilon _j : 1 \leq i \ne j \leq n\}$
form a root system of type
![]() $A_{n-1}$
. The simple roots
$A_{n-1}$
. The simple roots
![]() $\Pi =\{\alpha _1, \alpha _2, \ldots , \alpha _{n-1}\}$
are given by
$\Pi =\{\alpha _1, \alpha _2, \ldots , \alpha _{n-1}\}$
are given by
![]() $\alpha _i = \varepsilon _i - \varepsilon _{i+1}$
. A root
$\alpha _i = \varepsilon _i - \varepsilon _{i+1}$
. A root
![]() $\varepsilon _i - \varepsilon _j$
is positive if
$\varepsilon _i - \varepsilon _j$
is positive if
![]() $i < j$
and negative if
$i < j$
and negative if
![]() $i> j$
. The highest root (with respect to
$i> j$
. The highest root (with respect to
![]() $\Pi $
) is
$\Pi $
) is
![]() $\varepsilon _1 - \varepsilon _n$
. The bilinear form B is the Euclidean inner product on
$\varepsilon _1 - \varepsilon _n$
. The bilinear form B is the Euclidean inner product on
![]() ${\mathbb R}^n$
, and two roots are orthogonal if and only if they have disjoint support. The Weyl group is isomorphic to
${\mathbb R}^n$
, and two roots are orthogonal if and only if they have disjoint support. The Weyl group is isomorphic to
![]() $S_n$
and acts by permuting the standard basis
$S_n$
and acts by permuting the standard basis
![]() $\varepsilon _1,..,\varepsilon _n$
. The stabilizer
$\varepsilon _1,..,\varepsilon _n$
. The stabilizer
![]() $W_\alpha $
of each root
$W_\alpha $
of each root
![]() $\alpha $
is a Weyl group of type
$\alpha $
is a Weyl group of type
![]() $A_{n-3}$
, which is trivial if
$A_{n-3}$
, which is trivial if
![]() $n \leq 3$
.
$n \leq 3$
.
The vectors
![]() $\{\pm \varepsilon _i \pm \varepsilon _j : 1 \leq i < j \leq n\}$
form a root system of type
$\{\pm \varepsilon _i \pm \varepsilon _j : 1 \leq i < j \leq n\}$
form a root system of type
![]() $D_n$
. The simple roots
$D_n$
. The simple roots
![]() $\{\alpha _1, \alpha _2, \ldots , \alpha _n\}$
are given by
$\{\alpha _1, \alpha _2, \ldots , \alpha _n\}$
are given by
![]() $\alpha _i = \varepsilon _i - \varepsilon _{i+1}$
for
$\alpha _i = \varepsilon _i - \varepsilon _{i+1}$
for
![]() $i < n$
, and
$i < n$
, and
![]() $\alpha _n = \varepsilon _{n-1} + \varepsilon _{n}$
. If
$\alpha _n = \varepsilon _{n-1} + \varepsilon _{n}$
. If
![]() $i < j$
, then the roots
$i < j$
, then the roots
![]() $\varepsilon _i \pm \varepsilon _j$
are positive, and the roots
$\varepsilon _i \pm \varepsilon _j$
are positive, and the roots
![]() $-\varepsilon _i \pm \varepsilon _j$
are negative. The highest root is
$-\varepsilon _i \pm \varepsilon _j$
are negative. The highest root is
![]() $\varepsilon _1 + \varepsilon _2$
. The bilinear form B is the Euclidean inner product, and two roots
$\varepsilon _1 + \varepsilon _2$
. The bilinear form B is the Euclidean inner product, and two roots
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are orthogonal if and only if either (a)
$\beta $
are orthogonal if and only if either (a)
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
have disjoint support or (b)
$\beta $
have disjoint support or (b)
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
have the same support and
$\beta $
have the same support and
![]() $\alpha \ne \pm \beta $
. The Weyl group has order
$\alpha \ne \pm \beta $
. The Weyl group has order
![]() $2^{n-1}n!$
and acts by signed permutations of the standard basis, with the restriction that each element effects an even number of sign changes [Reference Humphreys33, Section 2.10]. The stabilizer of a root is a Weyl group of type
$2^{n-1}n!$
and acts by signed permutations of the standard basis, with the restriction that each element effects an even number of sign changes [Reference Humphreys33, Section 2.10]. The stabilizer of a root is a Weyl group of type
![]() $A_1 + D_{n-2}$
, meaning
$A_1 + D_{n-2}$
, meaning
![]() $W(A_1) \times W(D_{n-2})$
, where we interpret
$W(A_1) \times W(D_{n-2})$
, where we interpret
![]() $D_3$
as
$D_3$
as
![]() $A_3$
and
$A_3$
and
![]() $D_2$
as
$D_2$
as
![]() $A_1 + A_1$
. There is a well-known homomorphism
$A_1 + A_1$
. There is a well-known homomorphism
![]() $\phi $
from
$\phi $
from
![]() $W(D_{2n})$
to the symmetric group
$W(D_{2n})$
to the symmetric group
![]() $S_{2n}$
resulting from forgetting the signs in a signed permutation; it is given by the following formula:
$S_{2n}$
resulting from forgetting the signs in a signed permutation; it is given by the following formula:
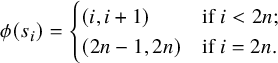
Let
![]() $\varepsilon _0, \varepsilon _1, \ldots , \varepsilon _7$
be the standard basis of
$\varepsilon _0, \varepsilon _1, \ldots , \varepsilon _7$
be the standard basis of
![]() ${\mathbb R}^8$
. The root system of type
${\mathbb R}^8$
. The root system of type
![]() $E_7$
may be regarded as a subset of
$E_7$
may be regarded as a subset of
![]() ${\mathbb R}^8$
as follows. There are 56 roots of the form
${\mathbb R}^8$
as follows. There are 56 roots of the form
![]() $\pm 2(\varepsilon _i - \varepsilon _j)$
where
$\pm 2(\varepsilon _i - \varepsilon _j)$
where
![]() $0 \leq i \ne j \leq 7$
, and there are 70 roots of the form
$0 \leq i \ne j \leq 7$
, and there are 70 roots of the form
![]() $\sum _{i = 0}^7 \pm \varepsilon _i$
, where the signs are chosen so that there are four
$\sum _{i = 0}^7 \pm \varepsilon _i$
, where the signs are chosen so that there are four
![]() $+$
and four
$+$
and four
![]() $-$
. The simple roots are
$-$
. The simple roots are
![]() $\alpha _1, \alpha _2, \ldots , \alpha _7$
, where
$\alpha _1, \alpha _2, \ldots , \alpha _7$
, where
![]() $\alpha _i = 2(\varepsilon _i - \varepsilon _{i+1})$
for
$\alpha _i = 2(\varepsilon _i - \varepsilon _{i+1})$
for
![]() $1 \leq i \leq 6$
, and
$1 \leq i \leq 6$
, and
A root of the form
![]() $2(\varepsilon _i - \varepsilon _j)$
is positive if
$2(\varepsilon _i - \varepsilon _j)$
is positive if
![]() $0 < i < j$
or
$0 < i < j$
or
![]() $j = 0$
, and negative otherwise. A root of the form
$j = 0$
, and negative otherwise. A root of the form
![]() $\sum _{i = 0}^7 \pm \varepsilon _i$
is positive if and only if
$\sum _{i = 0}^7 \pm \varepsilon _i$
is positive if and only if
![]() $\varepsilon _0$
occurs with negative coefficient. The highest root is
$\varepsilon _0$
occurs with negative coefficient. The highest root is
![]() $2(\varepsilon _1 - \varepsilon _0)$
. The bilinear form B is
$2(\varepsilon _1 - \varepsilon _0)$
. The bilinear form B is
![]() $1/4$
of the Euclidean inner product. The stabilizer of a root is a Weyl group of type
$1/4$
of the Euclidean inner product. The stabilizer of a root is a Weyl group of type
![]() $D_6$
. We call the coordinates
$D_6$
. We call the coordinates
![]() $\varepsilon _i$
Fano coordinates because they are particularly compatible with the combinatorics of the Fano plane; this will be important in Section 6.2.
$\varepsilon _i$
Fano coordinates because they are particularly compatible with the combinatorics of the Fano plane; this will be important in Section 6.2.
Let
![]() $\varepsilon _1, \varepsilon _2, \ldots , \varepsilon _8$
be the standard basis of
$\varepsilon _1, \varepsilon _2, \ldots , \varepsilon _8$
be the standard basis of
![]() ${\mathbb R}^8$
. The root system of type
${\mathbb R}^8$
. The root system of type
![]() $E_8$
may be regarded as a subset of
$E_8$
may be regarded as a subset of
![]() ${\mathbb R}^8$
as follows. There are 112 roots of the form
${\mathbb R}^8$
as follows. There are 112 roots of the form
![]() $\pm 2(\varepsilon _i \pm \varepsilon _j)$
where
$\pm 2(\varepsilon _i \pm \varepsilon _j)$
where
![]() $1 \leq i \ne j \leq 8$
, and there are 128 roots of the form
$1 \leq i \ne j \leq 8$
, and there are 128 roots of the form
![]() $\sum _{i = 1}^8 \pm \varepsilon _i$
, where the signs are chosen so that the total number of
$\sum _{i = 1}^8 \pm \varepsilon _i$
, where the signs are chosen so that the total number of
![]() $-$
is even. The simple roots are
$-$
is even. The simple roots are
![]() $\alpha _1, \alpha _2, \ldots , \alpha _8$
, where
$\alpha _1, \alpha _2, \ldots , \alpha _8$
, where
![]() $\alpha _2 = \varepsilon _1 + \varepsilon _2$
, and
$\alpha _2 = \varepsilon _1 + \varepsilon _2$
, and
![]() $\alpha _i = \varepsilon _{i-1} - \varepsilon _{i-2}$
for all
$\alpha _i = \varepsilon _{i-1} - \varepsilon _{i-2}$
for all
![]() $3 \leq i \leq 8$
. If k is the largest integer such that
$3 \leq i \leq 8$
. If k is the largest integer such that
![]() $\varepsilon _k$
appears in
$\varepsilon _k$
appears in
![]() $\alpha $
with nonzero coefficient c, then
$\alpha $
with nonzero coefficient c, then
![]() $\alpha $
is positive if and only if
$\alpha $
is positive if and only if
![]() $c> 0$
. The highest root is
$c> 0$
. The highest root is
![]() $2(\varepsilon _7 + \varepsilon _8)$
. The bilinear form B is
$2(\varepsilon _7 + \varepsilon _8)$
. The bilinear form B is
![]() $1/4$
of the Euclidean inner product. The stabilizer of a root is a Weyl group of type
$1/4$
of the Euclidean inner product. The stabilizer of a root is a Weyl group of type
![]() $E_7$
. We call the coordinates
$E_7$
. We call the coordinates
![]() $\varepsilon _i$
the standard coordinates for
$\varepsilon _i$
the standard coordinates for
![]() $E_8$
.
$E_8$
.
3 Combinatorics of coplanar quadruples
A matching of
![]() $[2n] := \{1, 2, \ldots , 2n\}$
is a collection of pairwise disjoint size-2 subsets, or 2-blocks, of
$[2n] := \{1, 2, \ldots , 2n\}$
is a collection of pairwise disjoint size-2 subsets, or 2-blocks, of
![]() $[2n]$
. The matching is perfect if the union of the 2-blocks is the whole of
$[2n]$
. The matching is perfect if the union of the 2-blocks is the whole of
![]() $[2n]$
. If
$[2n]$
. If
![]() $1 \leq a < b < c < d \leq 2n$
, then a crossing is a subset of the matching of the form
$1 \leq a < b < c < d \leq 2n$
, then a crossing is a subset of the matching of the form
![]() $\{\{a, c\}, \ \{b, d\}\}$
, a nesting is a subset of the form
$\{\{a, c\}, \ \{b, d\}\}$
, a nesting is a subset of the form
![]() $\{\{a, d\}, \ \{b, c\}\}$
, and an alignment is a subset of the form
$\{\{a, d\}, \ \{b, c\}\}$
, and an alignment is a subset of the form
![]() $\{\{a, b\}, \ \{c, d\}\}$
. For convenience, we will often denote each 2-block
$\{\{a, b\}, \ \{c, d\}\}$
. For convenience, we will often denote each 2-block
![]() $\{a,b\}$
in a matching simply by
$\{a,b\}$
in a matching simply by
![]() $ab$
from now on.
$ab$
from now on.
In this section, we generalize crossings, nestings and alignments to the notion of coplanar quadruples in the context of orthogonal sets of roots (Definition 3.9, Remark 3.11). As explained in the introduction, we can naturally identify each n-root
![]() $\alpha =\prod _{i=1}^n\beta _i$
in the Macdonald representation
$\alpha =\prod _{i=1}^n\beta _i$
in the Macdonald representation
![]() $j^{\Phi }_{nA_1}({\mathrm {sgn}})$
(Definition 1.1) with the set of its orthogonal components, and it turns out that coplanar quadruples are very useful for understanding the action of W on the orthogonal sets arising this way. We develop some key properties of coplanar quadruples in Theorem 3.10, which is the main result of Section 3. We also show that crossings, nestings and alignments can be distinguished from each other based on the heights of the roots that they contain (Proposition 3.13), and we give a precise description of the ways in which two coplanar quadruples can overlap (Proposition 3.20).
$j^{\Phi }_{nA_1}({\mathrm {sgn}})$
(Definition 1.1) with the set of its orthogonal components, and it turns out that coplanar quadruples are very useful for understanding the action of W on the orthogonal sets arising this way. We develop some key properties of coplanar quadruples in Theorem 3.10, which is the main result of Section 3. We also show that crossings, nestings and alignments can be distinguished from each other based on the heights of the roots that they contain (Proposition 3.13), and we give a precise description of the ways in which two coplanar quadruples can overlap (Proposition 3.20).
3.1 Coplanar quadruples
We gather a few facts about n-roots and define coplanar quadruples in this subsection. The following two results on maximal orthogonal sets of roots are well known, but we include proofs for ease of reference.
Lemma 3.1. Let W be a Weyl group of type
![]() $D_n$
for n even. Suppose that
$D_n$
for n even. Suppose that
![]() $n=2k\ge 4$
.
$n=2k\ge 4$
.
-
(i) Every maximal orthogonal set of roots is of the form
where we have $$ \begin{align*} \{& \pm(\varepsilon_{i_1} + \varepsilon_{j_1}),\ \pm(\varepsilon_{i_1} - \varepsilon_{j_1}),\ \pm(\varepsilon_{i_2} + \varepsilon_{j_2}),\ \pm(\varepsilon_{i_2} - \varepsilon_{j_2}),\ \ldots, & \pm(\varepsilon_{i_k} + \varepsilon_{j_k}),\ \pm(\varepsilon_{i_k} - \varepsilon_{j_k}) \},\end{align*} $$
$$ \begin{align*} \{& \pm(\varepsilon_{i_1} + \varepsilon_{j_1}),\ \pm(\varepsilon_{i_1} - \varepsilon_{j_1}),\ \pm(\varepsilon_{i_2} + \varepsilon_{j_2}),\ \pm(\varepsilon_{i_2} - \varepsilon_{j_2}),\ \ldots, & \pm(\varepsilon_{i_k} + \varepsilon_{j_k}),\ \pm(\varepsilon_{i_k} - \varepsilon_{j_k}) \},\end{align*} $$
 $\{i_1,j_1,\dots ,i_k,j_k\}=\{1,2,\dots , 2k-1,2k\}$
as sets and the signs are chosen independently.
$\{i_1,j_1,\dots ,i_k,j_k\}=\{1,2,\dots , 2k-1,2k\}$
as sets and the signs are chosen independently.
-
(ii) Every maximal orthogonal set of positive roots is of the form
and these sets are in bijection with perfect matchings $$ \begin{align*}\{ \varepsilon_{i_1} + \varepsilon_{j_1}, \ \varepsilon_{i_1} - \varepsilon_{j_1}, \ \varepsilon_{i_2} + \varepsilon_{j_2}, \ \varepsilon_{i_2} - \varepsilon_{j_2}, \ \ldots, \varepsilon_{i_k} + \varepsilon_{j_k}, \ \varepsilon_{i_k} - \varepsilon_{j_k} \} ,\end{align*} $$
$$ \begin{align*}\{ \varepsilon_{i_1} + \varepsilon_{j_1}, \ \varepsilon_{i_1} - \varepsilon_{j_1}, \ \varepsilon_{i_2} + \varepsilon_{j_2}, \ \varepsilon_{i_2} - \varepsilon_{j_2}, \ \ldots, \varepsilon_{i_k} + \varepsilon_{j_k}, \ \varepsilon_{i_k} - \varepsilon_{j_k} \} ,\end{align*} $$
 $\{ \{i_1, j_1\}, \ \{i_2, j_2\},\ \ldots , \{i_k, j_k\}\}$
of the set
$\{ \{i_1, j_1\}, \ \{i_2, j_2\},\ \ldots , \{i_k, j_k\}\}$
of the set
 $[n]$
that satisfy
$[n]$
that satisfy
 $i_r < j_r$
for all
$i_r < j_r$
for all
 $1 \leq r \leq k$
.
$1 \leq r \leq k$
.
Proof. Let R be a maximal orthogonal set of roots. By symmetry, we may reduce to the case where all the roots in R are positive. If R contains the root
![]() $\varepsilon _i \pm \varepsilon _j$
, then R must also contain the root
$\varepsilon _i \pm \varepsilon _j$
, then R must also contain the root
![]() $\varepsilon _i \mp \varepsilon _j$
because otherwise
$\varepsilon _i \mp \varepsilon _j$
because otherwise
![]() $R \cup \{\varepsilon _i \mp \varepsilon _j\}$
would be a set of orthogonal roots that was larger than R. It follows that R consists of
$R \cup \{\varepsilon _i \mp \varepsilon _j\}$
would be a set of orthogonal roots that was larger than R. It follows that R consists of
![]() $n/2$
pairs of roots such that each pair has the same support, and roots from distinct pairs have disjoint supports. This completes the proof of (i).
$n/2$
pairs of roots such that each pair has the same support, and roots from distinct pairs have disjoint supports. This completes the proof of (i).
Part (ii) follows from (i) and the fact that if
![]() $1 \leq i < j \leq n$
, then the roots
$1 \leq i < j \leq n$
, then the roots
![]() $\varepsilon _i \pm \varepsilon _j$
are positive.
$\varepsilon _i \pm \varepsilon _j$
are positive.
It follows from Lemma 3.1 (ii) that a maximal orthogonal set of positive roots in type
![]() $D_n$
(for n even) contains the root
$D_n$
(for n even) contains the root
![]() $\varepsilon _i - \varepsilon _j$
if and only if it contains the root
$\varepsilon _i - \varepsilon _j$
if and only if it contains the root
![]() $\varepsilon _i + \varepsilon _j$
. We will call such a pair of roots
$\varepsilon _i + \varepsilon _j$
. We will call such a pair of roots
![]() $\{\varepsilon _i \pm \varepsilon _j\}$
a collinear pair of roots.
$\{\varepsilon _i \pm \varepsilon _j\}$
a collinear pair of roots.
Lemma 3.2. If W is a Weyl group of type
![]() $E_7$
,
$E_7$
,
![]() $E_8$
or
$E_8$
or
![]() $D_n$
with
$D_n$
with
![]() $n \geq 4$
even, then W acts transitively on the set
$n \geq 4$
even, then W acts transitively on the set
![]() $\mathcal {M}(W)$
of unordered maximal sets of orthogonal roots of W.
$\mathcal {M}(W)$
of unordered maximal sets of orthogonal roots of W.
Proof. Recall from Section 2 that the group
![]() $W(D_n)$
can be regarded as the group of signed permutations of n objects in which there is an even number of sign changes. Such a group acts transitively on the set described in Lemma 3.1 (i).
$W(D_n)$
can be regarded as the group of signed permutations of n objects in which there is an even number of sign changes. Such a group acts transitively on the set described in Lemma 3.1 (i).
Now suppose W has type
![]() $E_7$
, and let
$E_7$
, and let
![]() $\alpha $
be a root of W. Then by Section 2, the stabilizer
$\alpha $
be a root of W. Then by Section 2, the stabilizer
![]() $W_\alpha $
is a Weyl group of type
$W_\alpha $
is a Weyl group of type
![]() $D_6$
whose root system is the set
$D_6$
whose root system is the set
![]() $\Phi _\alpha $
of roots that are orthogonal to
$\Phi _\alpha $
of roots that are orthogonal to
![]() $\alpha $
. Since
$\alpha $
. Since
![]() $W_\alpha $
acts transitively on
$W_\alpha $
acts transitively on
![]() $\Phi _\alpha $
, it follows that there is a well-defined bijection
$\Phi _\alpha $
, it follows that there is a well-defined bijection
![]() $[R]\mapsto [R\cup \{\alpha \}]$
from the set of
$[R]\mapsto [R\cup \{\alpha \}]$
from the set of
![]() $W_\alpha $
-orbits on
$W_\alpha $
-orbits on
![]() $\mathcal {M}(W_\alpha )$
to the set of W-orbits on
$\mathcal {M}(W_\alpha )$
to the set of W-orbits on
![]() $\mathcal {M}(W)$
, where the orbit
$\mathcal {M}(W)$
, where the orbit
![]() $[R]$
of every 6-tuple
$[R]$
of every 6-tuple
![]() $R\in \mathcal {M}(W_\alpha )$
is sent to the orbit
$R\in \mathcal {M}(W_\alpha )$
is sent to the orbit
![]() $[R\cup \{\alpha \}]$
of the 7-tuple
$[R\cup \{\alpha \}]$
of the 7-tuple
![]() $R\cup \{\alpha \}$
. It then follows that W acts transitively on
$R\cup \{\alpha \}$
. It then follows that W acts transitively on
![]() $\mathcal {M}(W)$
, as desired.
$\mathcal {M}(W)$
, as desired.
Finally, if W has type
![]() $E_8$
, then for each root
$E_8$
, then for each root
![]() $\alpha $
of W, the stablizer
$\alpha $
of W, the stablizer
![]() $W_\alpha $
is of type
$W_\alpha $
is of type
![]() $E_7$
. A similar argument to the one above shows that W acts transitively on
$E_7$
. A similar argument to the one above shows that W acts transitively on
![]() $\mathcal {M}(W)$
because
$\mathcal {M}(W)$
because
![]() $W_\alpha $
acts transitively on
$W_\alpha $
acts transitively on
![]() $\mathcal {M}(W_\alpha )$
.
$\mathcal {M}(W_\alpha )$
.
We are ready to define coplanar quadruples. The following proposition offers multiple equivalent characterizations of them.
Proposition 3.3. Let
![]() $Q = \{\beta _1, \beta _2, \beta _3, \beta _4\}$
be a set of four mutually orthogonal roots for a simply laced Weyl group W with root system
$Q = \{\beta _1, \beta _2, \beta _3, \beta _4\}$
be a set of four mutually orthogonal roots for a simply laced Weyl group W with root system
![]() $\Phi $
, and let
$\Phi $
, and let
![]() $\gamma = (\beta _1 + \beta _2 + \beta _3 + \beta _4)/2$
. The following are equivalent:
$\gamma = (\beta _1 + \beta _2 + \beta _3 + \beta _4)/2$
. The following are equivalent:
-
(i)
 $\gamma $
is a root (i.e., the elements of Q sum to twice a root);
$\gamma $
is a root (i.e., the elements of Q sum to twice a root); -
(ii) Q is contained in a subsystem
 $\Psi $
of type
$\Psi $
of type
 $D_4$
;
$D_4$
; -
(iii) there is a unique subsystem
 $\Psi $
of type
$\Psi $
of type
 $D_4$
such that
$D_4$
such that
 $(Q\cup \{\gamma \}) \subset \Psi \subseteq \Phi $
, and we have where all the signs are chosen independently.
$(Q\cup \{\gamma \}) \subset \Psi \subseteq \Phi $
, and we have where all the signs are chosen independently. $$ \begin{align*}\Psi = \left\{\pm \beta_1, \ \pm \beta_2, \ \pm \beta_3, \ \pm \beta_4, \ (\pm \beta_1 \pm \beta_2 \pm \beta_3 \pm \beta_4)/2\right\} ,\end{align*} $$
$$ \begin{align*}\Psi = \left\{\pm \beta_1, \ \pm \beta_2, \ \pm \beta_3, \ \pm \beta_4, \ (\pm \beta_1 \pm \beta_2 \pm \beta_3 \pm \beta_4)/2\right\} ,\end{align*} $$
Proof. We first prove that (i) implies (iii). Assume that
![]() $\gamma $
is a root. Any root subsystem containing
$\gamma $
is a root. Any root subsystem containing
![]() $Q\cup \{\gamma \}$
also contains
$Q\cup \{\gamma \}$
also contains
![]() $s_{\beta _i}(\beta _i) = -\beta _i$
for each i, as well as all roots of the form
$s_{\beta _i}(\beta _i) = -\beta _i$
for each i, as well as all roots of the form
where we have
![]() $\epsilon _i \in \{0, 1\}$
for all i. The 16 roots listed above can also be expressed as
$\epsilon _i \in \{0, 1\}$
for all i. The 16 roots listed above can also be expressed as
We have constructed all 24 roots in the set
![]() $\Psi $
listed in the statement, and this is the cardinality of a root system of type
$\Psi $
listed in the statement, and this is the cardinality of a root system of type
![]() $D_4$
. To prove (iii), it now suffices to show that
$D_4$
. To prove (iii), it now suffices to show that
![]() $\Psi $
is a root system of type
$\Psi $
is a root system of type
![]() $D_4$
. Because the elements of Q are orthogonal vectors of the same length, we may choose Euclidean coordinates
$D_4$
. Because the elements of Q are orthogonal vectors of the same length, we may choose Euclidean coordinates
![]() $\beta _1 = \varepsilon _1 - \varepsilon _2$
,
$\beta _1 = \varepsilon _1 - \varepsilon _2$
,
![]() $\beta _2 = \varepsilon _1 + \varepsilon _2$
,
$\beta _2 = \varepsilon _1 + \varepsilon _2$
,
![]() $\beta _3 = \varepsilon _3 - \varepsilon _4$
and
$\beta _3 = \varepsilon _3 - \varepsilon _4$
and
![]() $\beta _4 = \varepsilon _3 + \varepsilon _4$
. With respect to these coordinates, we have
$\beta _4 = \varepsilon _3 + \varepsilon _4$
. With respect to these coordinates, we have
which indeed forms a root system of type
![]() $D_4$
, as desired.
$D_4$
, as desired.
It is immediate that (iii) implies (ii).
In the usual notation for the simple roots of type
![]() $D_4$
, the orthogonal roots
$D_4$
, the orthogonal roots
![]() $\alpha _1$
,
$\alpha _1$
,
![]() $\alpha _3$
,
$\alpha _3$
,
![]() $\alpha _4$
, and
$\alpha _4$
, and
![]() $\alpha _1 + 2\alpha _2 + \alpha _3 + \alpha _4$
sum to
$\alpha _1 + 2\alpha _2 + \alpha _3 + \alpha _4$
sum to
![]() $2 \alpha $
, where
$2 \alpha $
, where
![]() $\alpha $
is the root
$\alpha $
is the root
![]() $\alpha _1 + \alpha _2 + \alpha _3 + \alpha _4$
. Lemma 3.2 applied to a root system of type
$\alpha _1 + \alpha _2 + \alpha _3 + \alpha _4$
. Lemma 3.2 applied to a root system of type
![]() $D_4$
then implies that the sum of every orthogonal quadruple of roots in a root system of type
$D_4$
then implies that the sum of every orthogonal quadruple of roots in a root system of type
![]() $D_4$
is equal to
$D_4$
is equal to
![]() $2 \alpha '$
for some root
$2 \alpha '$
for some root
![]() $\alpha '$
. It follows that (ii) implies (i), which completes the proof.
$\alpha '$
. It follows that (ii) implies (i), which completes the proof.
Definition 3.4. A set Q of four mutually orthogonal roots for a simply laced Weyl group is called a coplanar quadruple if it satisfies the equivalent conditions of Proposition 3.3. In this case, we call the set
![]() $\Psi $
from Proposition 3.3 the
$\Psi $
from Proposition 3.3 the
![]() $D_4$
-subsystem associated to Q.
$D_4$
-subsystem associated to Q.
Coplanar quadruples can be described explicitly in coordinates in type D:
Lemma 3.5. Let W be a Weyl group of type
![]() $D_n$
for n even and
$D_n$
for n even and
![]() $n\ge 4$
. Then four positive roots of W form a coplanar quadruple if and only if they consist of two collinear pairs of roots (i.e., if and only if they are of the form
$n\ge 4$
. Then four positive roots of W form a coplanar quadruple if and only if they consist of two collinear pairs of roots (i.e., if and only if they are of the form
![]() $\varepsilon _i+\varepsilon _j, \varepsilon _i-\varepsilon _j, \varepsilon _k+\varepsilon _l,\varepsilon _k-\varepsilon _l$
for four distinct indices
$\varepsilon _i+\varepsilon _j, \varepsilon _i-\varepsilon _j, \varepsilon _k+\varepsilon _l,\varepsilon _k-\varepsilon _l$
for four distinct indices
![]() $i,j,k,l$
where
$i,j,k,l$
where
![]() $i<j$
and
$i<j$
and
![]() $k<l$
).
$k<l$
).
Remark 3.6. In the setting of Lemma 3.5, we may naturally identify the coplanar quadruple
![]() $\{\varepsilon _i\pm \varepsilon _j,\varepsilon _k\pm \varepsilon _l\}$
with the matching
$\{\varepsilon _i\pm \varepsilon _j,\varepsilon _k\pm \varepsilon _l\}$
with the matching
![]() $\{ij,kl\}$
of the set
$\{ij,kl\}$
of the set
![]() $\{i,j,k,l\}$
.
$\{i,j,k,l\}$
.
Remark 3.7. Recall that reflections in
![]() $W(D_n)$
act on the reflection representation as signed permutations, with
$W(D_n)$
act on the reflection representation as signed permutations, with
![]() $s_{\alpha }(\varepsilon _i)=\varepsilon _j$
if
$s_{\alpha }(\varepsilon _i)=\varepsilon _j$
if
![]() $\alpha =\varepsilon _i-\varepsilon _j$
and
$\alpha =\varepsilon _i-\varepsilon _j$
and
![]() $s_\alpha (\varepsilon _i)=-\varepsilon _j$
if
$s_\alpha (\varepsilon _i)=-\varepsilon _j$
if
![]() $\alpha =\varepsilon _i+\varepsilon _j$
. It follows that
$\alpha =\varepsilon _i+\varepsilon _j$
. It follows that
![]() $W(D_n)$
acts on the set
$W(D_n)$
acts on the set
![]() $\{\varepsilon _1^2,\cdots ,\varepsilon _n^2\}$
as ordinary permutations, with
$\{\varepsilon _1^2,\cdots ,\varepsilon _n^2\}$
as ordinary permutations, with
![]() $s_\alpha (\varepsilon _i^2)=\varepsilon _j^2$
for all distinct
$s_\alpha (\varepsilon _i^2)=\varepsilon _j^2$
for all distinct
![]() $i, j$
. When n is even, it then follows from Lemmas 3.1 and 3.5 that the action of
$i, j$
. When n is even, it then follows from Lemmas 3.1 and 3.5 that the action of
![]() $W(D_n)$
on n-roots factors through the map
$W(D_n)$
on n-roots factors through the map
![]() $\phi :W(D_n)\rightarrow S_n$
from Equation (2.2) to induce an action of
$\phi :W(D_n)\rightarrow S_n$
from Equation (2.2) to induce an action of
![]() $S_n$
on n-roots. In particular, each reflection
$S_n$
on n-roots. In particular, each reflection
![]() $r\in W(D_n)$
acts in the same way as
$r\in W(D_n)$
acts in the same way as
![]() $\phi (r)$
on every n-root of
$\phi (r)$
on every n-root of
![]() $W(D_n)$
.
$W(D_n)$
.
Proof of Lemma 3.5.
The ‘if’ implication holds since the four roots in the given form sum to twice the positive root
![]() $\varepsilon _i+\varepsilon _k$
. To prove the ‘only if’ implication, let
$\varepsilon _i+\varepsilon _k$
. To prove the ‘only if’ implication, let
![]() $Q=\{\beta _1,\beta _2,\beta _3,\beta _4\}$
be a coplanar quadruple. Recall from Section 2 that two roots in type
$Q=\{\beta _1,\beta _2,\beta _3,\beta _4\}$
be a coplanar quadruple. Recall from Section 2 that two roots in type
![]() $D_n$
are orthogonal if and only if they have the same or disjoint support. It follows that if no two roots in Q have the same support, then the supports of
$D_n$
are orthogonal if and only if they have the same or disjoint support. It follows that if no two roots in Q have the same support, then the supports of
![]() $\beta _1,\beta _2,\beta _3,\beta _4$
contain a total of eight distinct coordinates
$\beta _1,\beta _2,\beta _3,\beta _4$
contain a total of eight distinct coordinates
![]() $\varepsilon _i$
, in which case the sum
$\varepsilon _i$
, in which case the sum
![]() $\gamma =\beta _1+\beta _2+\beta _3+\beta _4$
cannot be twice a root. We may therefore assume, without loss of generality, that
$\gamma =\beta _1+\beta _2+\beta _3+\beta _4$
cannot be twice a root. We may therefore assume, without loss of generality, that
![]() $\{\beta _1,\beta _2\}=\{\varepsilon _i\pm \varepsilon _j\}$
for some
$\{\beta _1,\beta _2\}=\{\varepsilon _i\pm \varepsilon _j\}$
for some
![]() $i<j$
. This implies
$i<j$
. This implies
![]() $\beta _1+\beta _2=2\varepsilon _i$
. The condition that Q is an orthogonal set summing to twice a root then forces us to have
$\beta _1+\beta _2=2\varepsilon _i$
. The condition that Q is an orthogonal set summing to twice a root then forces us to have
![]() $\{\beta _3,\beta _4\}=\{\varepsilon _k\pm \varepsilon _l\}$
for some elements
$\{\beta _3,\beta _4\}=\{\varepsilon _k\pm \varepsilon _l\}$
for some elements
![]() $k,l$
distinct from i and j with
$k,l$
distinct from i and j with
![]() $k<l$
.
$k<l$
.
The next proposition shows that the action of W on n-roots is local to coplanar quadruples in the following sense: whenever a reflection in W does not fix a maximal orthogonal set R of roots, it must change exactly four elements of R that form a coplanar quadruple, and it changes these four elements to another coplanar quadruple with the same associated
![]() $D_4$
-subsystem.
$D_4$
-subsystem.
Proposition 3.8. Let W be a Weyl group of type
![]() $E_7$
,
$E_7$
,
![]() $E_8$
or
$E_8$
or
![]() $D_n$
for n even, let
$D_n$
for n even, let
![]() $\alpha $
be a root, and let R be a maximal set of orthogonal positive roots. Suppose that neither
$\alpha $
be a root, and let R be a maximal set of orthogonal positive roots. Suppose that neither
![]() $\alpha $
nor
$\alpha $
nor
![]() $-\alpha $
is an element of R.
$-\alpha $
is an element of R.
-
(i) The root
 $\alpha $
is orthogonal to all but precisely four elements
$\alpha $
is orthogonal to all but precisely four elements
 $Q = \{\beta _1, \beta _2, \beta _3, \beta _4\}$
of R. The elements of Q form a coplanar quadruple, and we have
$Q = \{\beta _1, \beta _2, \beta _3, \beta _4\}$
of R. The elements of Q form a coplanar quadruple, and we have
 $ 2\alpha = \pm \beta _1 \pm \beta _2 \pm \beta _3 \pm \beta _4$
for suitable choices of signs.
$ 2\alpha = \pm \beta _1 \pm \beta _2 \pm \beta _3 \pm \beta _4$
for suitable choices of signs. -
(ii) Let
 $\Psi $
be the
$\Psi $
be the
 $D_4$
subsystem associated to Q. Then we have
$D_4$
subsystem associated to Q. Then we have
 $\alpha \in \Psi $
, and the set
$\alpha \in \Psi $
, and the set
 $s_\alpha (Q)=\{s_\alpha (\beta _i):1\le i\le 4\}$
is also a coplanar quadruple whose associated
$s_\alpha (Q)=\{s_\alpha (\beta _i):1\le i\le 4\}$
is also a coplanar quadruple whose associated
 $D_4$
-subsystem is
$D_4$
-subsystem is
 $\Psi $
.
$\Psi $
.
Proof. To prove (i), it suffices by Lemma 3.2 to do so for a fixed R. Suppose first that W is of type
![]() $D_n$
, and choose
$D_n$
, and choose
The root
![]() $\alpha $
must be of the form
$\alpha $
must be of the form
![]() $\pm \varepsilon _i \pm \varepsilon _j$
, where i and j come from different parts of the partition
$\pm \varepsilon _i \pm \varepsilon _j$
, where i and j come from different parts of the partition
![]() $\{\{1, 2\}, \{3, 4\}, \ldots , \{n-1, n\}\}$
. It follows that the support of
$\{\{1, 2\}, \{3, 4\}, \ldots , \{n-1, n\}\}$
. It follows that the support of
![]() $\alpha $
has one element in common with the support of each of precisely four elements of R making up two collinear pairs, and that
$\alpha $
has one element in common with the support of each of precisely four elements of R making up two collinear pairs, and that
![]() $\alpha $
is orthogonal to all the other elements of R. Furthermore, the roots
$\alpha $
is orthogonal to all the other elements of R. Furthermore, the roots
![]() $\beta _1$
,
$\beta _1$
,
![]() $\beta _2$
,
$\beta _2$
,
![]() $\beta _3$
and
$\beta _3$
and
![]() $\beta _4$
that are not orthogonal to
$\beta _4$
that are not orthogonal to
![]() $\alpha $
are of the form
$\alpha $
are of the form
![]() $\pm \varepsilon _h \pm \varepsilon _i$
and
$\pm \varepsilon _h \pm \varepsilon _i$
and
![]() $\pm \varepsilon _j \pm \varepsilon _k$
, where
$\pm \varepsilon _j \pm \varepsilon _k$
, where
![]() $|\{h, i, j, k\}| = 4$
. It follows that
$|\{h, i, j, k\}| = 4$
. It follows that
![]() $2\alpha $
can be written in the form
$2\alpha $
can be written in the form
![]() $\pm \beta _1\pm \beta _2\pm \beta _3\pm \beta _4$
for suitable choices of signs.
$\pm \beta _1\pm \beta _2\pm \beta _3\pm \beta _4$
for suitable choices of signs.
Next, suppose that W has type
![]() $E_8$
, and choose
$E_8$
, and choose
If
![]() $\alpha $
has the form
$\alpha $
has the form
![]() $2(\pm \varepsilon _i \pm \varepsilon _j)$
, then the proof is completed using the same argument as in type
$2(\pm \varepsilon _i \pm \varepsilon _j)$
, then the proof is completed using the same argument as in type
![]() $D_8$
. The other possibility is that we have
$D_8$
. The other possibility is that we have
![]() $\alpha = \sum _{i = 1}^8 \pm \varepsilon _i$
, where the signs are chosen so that there is an even number of minus signs. In this case,
$\alpha = \sum _{i = 1}^8 \pm \varepsilon _i$
, where the signs are chosen so that there is an even number of minus signs. In this case,
![]() $\alpha $
is orthogonal to precisely one of the roots
$\alpha $
is orthogonal to precisely one of the roots
![]() $\{2(\varepsilon _j - \varepsilon _{j+1}), \ 2(\varepsilon _j + \varepsilon _{j+1})\}$
, according as
$\{2(\varepsilon _j - \varepsilon _{j+1}), \ 2(\varepsilon _j + \varepsilon _{j+1})\}$
, according as
![]() $\varepsilon _j$
and
$\varepsilon _j$
and
![]() $\varepsilon _{j+1}$
occur in
$\varepsilon _{j+1}$
occur in
![]() $\alpha $
with the same or with opposite coefficients. It follows that
$\alpha $
with the same or with opposite coefficients. It follows that
![]() $\alpha $
is orthogonal to precisely four elements of R and that
$\alpha $
is orthogonal to precisely four elements of R and that
![]() $2 \alpha $
can be expressed in the required form.
$2 \alpha $
can be expressed in the required form.
Now suppose that W has type
![]() $E_7$
. By Section 2.3, we may identify the root system of W with the set of roots orthogonal to the highest root
$E_7$
. By Section 2.3, we may identify the root system of W with the set of roots orthogonal to the highest root
![]() $\theta $
in the root system of type
$\theta $
in the root system of type
![]() $E_8$
, so that
$E_8$
, so that
![]() $R \cup \{\theta \}$
is a maximal set of orthogonal roots in type
$R \cup \{\theta \}$
is a maximal set of orthogonal roots in type
![]() $E_8$
. By the above paragraph,
$E_8$
. By the above paragraph,
![]() $\alpha $
is orthogonal to four of the roots in
$\alpha $
is orthogonal to four of the roots in
![]() $R \cup \{\theta \}$
, but one of these roots is
$R \cup \{\theta \}$
, but one of these roots is
![]() $\theta $
itself. It follows that
$\theta $
itself. It follows that
![]() $\alpha $
is orthogonal to three elements of R and that
$\alpha $
is orthogonal to three elements of R and that
![]() $2 \alpha $
can be expressed as a signed sum of the other four elements of R, as required. This completes the proof of (i).
$2 \alpha $
can be expressed as a signed sum of the other four elements of R, as required. This completes the proof of (i).
It follows from (i) that we have
![]() $\alpha \in \Psi $
, because condition (i) implies condition (iii) in Proposition 3.3. The element
$\alpha \in \Psi $
, because condition (i) implies condition (iii) in Proposition 3.3. The element
![]() $\gamma =(\beta _1+\beta _2+\beta _3+\beta _4)/2$
is a root because Q is a coplanar quadruple, and the set
$\gamma =(\beta _1+\beta _2+\beta _3+\beta _4)/2$
is a root because Q is a coplanar quadruple, and the set
![]() $s_\alpha (Q)$
is a coplanar quadruple because its elements sum to twice
$s_\alpha (Q)$
is a coplanar quadruple because its elements sum to twice
![]() $s_\alpha (\gamma )$
, which is a root because
$s_\alpha (\gamma )$
, which is a root because
![]() $\gamma $
is. We also have
$\gamma $
is. We also have
![]() $s_\alpha (Q)\subseteq \Psi $
because both
$s_\alpha (Q)\subseteq \Psi $
because both
![]() $\alpha $
and Q are in
$\alpha $
and Q are in
![]() $\Psi $
. This implies that
$\Psi $
. This implies that
![]() $\Psi $
must be the
$\Psi $
must be the
![]() $D_4$
-subsystem associated to
$D_4$
-subsystem associated to
![]() $s_\alpha (Q)$
, proving (ii).
$s_\alpha (Q)$
, proving (ii).
3.2 Crossings, nestings and alignments
We examine coplanar quadruples more closely in this subsection and classify them into three types – namely, crossings, nestings and alignments. As we will explain in Remark 3.11, our terminology comes from the theory of matchings, but the following definition makes sense for all the simply laced root systems considered in this paper.
Definition 3.9. Let
![]() $Q = \{\beta _1, \beta _2, \beta _3, \beta _4\}$
be a coplanar quadruple of positive orthogonal roots, let
$Q = \{\beta _1, \beta _2, \beta _3, \beta _4\}$
be a coplanar quadruple of positive orthogonal roots, let
![]() $\Psi $
be the
$\Psi $
be the
![]() $D_4$
-subsystem associated to Q, let
$D_4$
-subsystem associated to Q, let
![]() $\leq $
be the partial order on
$\leq $
be the partial order on
![]() $\Psi $
relative to the induced simple roots of
$\Psi $
relative to the induced simple roots of
![]() $\Psi $
, and let
$\Psi $
, and let
![]() $\gamma $
be the root
$\gamma $
be the root
![]() $(\beta _1 + \beta _2 + \beta _3 + \beta _4)/2$
. We say that Q is
$(\beta _1 + \beta _2 + \beta _3 + \beta _4)/2$
. We say that Q is
-
(i) a crossing if
 $\beta _i \leq \gamma $
for all i and Q contains the unique
$\beta _i \leq \gamma $
for all i and Q contains the unique
 $\leq $
-maximal element of
$\leq $
-maximal element of
 $Q \cup (-s_\gamma (Q))$
;
$Q \cup (-s_\gamma (Q))$
; -
(ii) a nesting if
 $\beta _i \leq \gamma $
for all i and Q contains the unique
$\beta _i \leq \gamma $
for all i and Q contains the unique
 $\leq $
-minimal element of
$\leq $
-minimal element of
 $Q \cup (-s_\gamma (Q))$
;
$Q \cup (-s_\gamma (Q))$
; -
(iii) an alignment otherwise.
We also call each crossing, nesting and alignment a feature of type C, type N and type A, respectively.
Theorem 3.10. Let
![]() $\Phi $
be a root system for a Weyl group of type
$\Phi $
be a root system for a Weyl group of type
![]() $E_7$
,
$E_7$
,
![]() $E_8$
or
$E_8$
or
![]() $D_n$
for n even. Let Q be a coplanar quadruple of positive roots of
$D_n$
for n even. Let Q be a coplanar quadruple of positive roots of
![]() $\Phi $
, let
$\Phi $
, let
![]() $\Psi $
be the associated
$\Psi $
be the associated
![]() $D_4$
-subsystem, and let
$D_4$
-subsystem, and let
![]() $\Psi ^+ = \Psi \cap \Phi ^+$
be the induced positive system of
$\Psi ^+ = \Psi \cap \Phi ^+$
be the induced positive system of
![]() $\Psi $
.
$\Psi $
.
-
(i) The set
 $\Psi ^+$
contains precisely three distinct quadruples of mutually orthogonal roots. These quadruples are pairwise disjoint and partition
$\Psi ^+$
contains precisely three distinct quadruples of mutually orthogonal roots. These quadruples are pairwise disjoint and partition
 $\Psi ^+$
.
$\Psi ^+$
. -
(ii) The three quadruples of orthogonal roots in
 $\Psi ^+$
are all coplanar. Among them there is exactly one crossing,
$\Psi ^+$
are all coplanar. Among them there is exactly one crossing,
 $\Psi ^+_C$
, exactly one nesting,
$\Psi ^+_C$
, exactly one nesting,
 $\Psi ^+_N$
, and exactly one alignment,
$\Psi ^+_N$
, and exactly one alignment,
 $\Psi ^+_A$
. In particular, the quadruple Q cannot be both a crossing and a nesting, and the three conditions in Definition 3.9 are mutually exclusive.
$\Psi ^+_A$
. In particular, the quadruple Q cannot be both a crossing and a nesting, and the three conditions in Definition 3.9 are mutually exclusive. -
(iii) Each quadruple in
 $\{\Psi ^+_C,\Psi ^+_N, \Psi ^+_A\}$
uniquely determines both of the other two.
$\{\Psi ^+_C,\Psi ^+_N, \Psi ^+_A\}$
uniquely determines both of the other two. -
(iv) If R is a set of mutually orthogonal roots that is disjoint from
 $\Psi $
, then either each of the three sets
$\Psi $
, then either each of the three sets
 $\{R \cup \Psi ^+_C, \ R \cup \Psi ^+_N, \ R \cup \Psi ^+_A\}$
consists of mutually orthogonal roots, or none of them does.
$\{R \cup \Psi ^+_C, \ R \cup \Psi ^+_N, \ R \cup \Psi ^+_A\}$
consists of mutually orthogonal roots, or none of them does. -
(v) The crossing
 $\Psi ^+_C$
contains no root from the induced simple system of
$\Psi ^+_C$
contains no root from the induced simple system of
 $\Psi $
.
$\Psi $
. -
(vi) For each
 $x\in \{C,N,A\}$
, let
$x\in \{C,N,A\}$
, let
 $\gamma _x$
be the product of the roots in
$\gamma _x$
be the product of the roots in
 $\Psi ^+_x$
, and let
$\Psi ^+_x$
, and let
 $\sigma (\gamma _x)$
be the sum of the components of
$\sigma (\gamma _x)$
be the sum of the components of
 $\gamma _x$
. Then we have
$\gamma _x$
. Then we have
 $\sigma (\gamma _A) < \sigma (\gamma _N) = \sigma (\gamma _C)$
and
$\sigma (\gamma _A) < \sigma (\gamma _N) = \sigma (\gamma _C)$
and
 $\gamma _C = \gamma _N + \gamma _A.$
Moreover, if
$\gamma _C = \gamma _N + \gamma _A.$
Moreover, if
 $\alpha $
is any component in one of the three
$\alpha $
is any component in one of the three
 $4$
-roots
$4$
-roots
 $\gamma _C,\gamma _N$
and
$\gamma _C,\gamma _N$
and
 $\gamma _A$
, then the reflection
$\gamma _A$
, then the reflection
 $s_\alpha $
sends the other two
$s_\alpha $
sends the other two
 $4$
-roots to each other; for example, if
$4$
-roots to each other; for example, if
 $\alpha \in \Psi ^+_C$
, then
$\alpha \in \Psi ^+_C$
, then
 $s_\alpha $
sends
$s_\alpha $
sends
 $\gamma _N$
and
$\gamma _N$
and
 $\gamma _A$
to each other.
$\gamma _A$
to each other.
Proof. By Section 2.3, the roots orthogonal to a given root in type
![]() $D_4$
form a subsystem of type
$D_4$
form a subsystem of type
![]() $3A_1$
. Therefore, each positive root lies in a unique quadruple of mutually orthogonal positive roots, which proves (i).
$3A_1$
. Therefore, each positive root lies in a unique quadruple of mutually orthogonal positive roots, which proves (i).
Let
![]() $\{\alpha _1,\alpha _2,\alpha _3,\alpha _4\}$
be the induced simple roots of
$\{\alpha _1,\alpha _2,\alpha _3,\alpha _4\}$
be the induced simple roots of
![]() $\Psi $
, with
$\Psi $
, with
![]() $\alpha _2$
corresponding to the branch node in the Dynkin diagram. Then the three quadruples from (i) are given by
$\alpha _2$
corresponding to the branch node in the Dynkin diagram. Then the three quadruples from (i) are given by
The roots in
![]() $\Psi ^+_3$
add up to twice the root
$\Psi ^+_3$
add up to twice the root
![]() $\alpha = \alpha _1 + \alpha _2 + \alpha _3 + \alpha _4$
. The root
$\alpha = \alpha _1 + \alpha _2 + \alpha _3 + \alpha _4$
. The root
![]() $\alpha $
is strictly lower in the
$\alpha $
is strictly lower in the
![]() $\le $
order than one of the roots in
$\le $
order than one of the roots in
![]() $\Psi ^+_3$
; therefore,
$\Psi ^+_3$
; therefore,
![]() $\Psi ^+_3$
is an alignment by Definition 3.9. The roots in
$\Psi ^+_3$
is an alignment by Definition 3.9. The roots in
![]() $\Psi ^+_1$
and
$\Psi ^+_1$
and
![]() $\Psi ^+_2$
both add up to
$\Psi ^+_2$
both add up to
![]() $2 \theta $
, where
$2 \theta $
, where
![]() $\theta = \alpha _1 + 2\alpha _2 + \alpha _3 + \alpha _4$
. The root
$\theta = \alpha _1 + 2\alpha _2 + \alpha _3 + \alpha _4$
. The root
![]() $\theta $
is strictly higher in the
$\theta $
is strictly higher in the
![]() $\le $
order than each element of
$\le $
order than each element of
![]() $\Psi ^+_1$
and
$\Psi ^+_1$
and
![]() $\Psi ^+_2$
. Note that we have
$\Psi ^+_2$
. Note that we have
![]() $s_\theta (\Psi ^+_1) = -\Psi ^+_2$
and
$s_\theta (\Psi ^+_1) = -\Psi ^+_2$
and
![]() $s_\theta (\Psi ^+_2) = -\Psi ^+_1$
. Furthermore, the roots
$s_\theta (\Psi ^+_2) = -\Psi ^+_1$
. Furthermore, the roots
![]() $\alpha _2$
and
$\alpha _2$
and
![]() $\alpha _1 + \alpha _2 + \alpha _3 + \alpha _4$
are the unique
$\alpha _1 + \alpha _2 + \alpha _3 + \alpha _4$
are the unique
![]() $\leq $
-minimal and unique
$\leq $
-minimal and unique
![]() $\leq $
-maximal elements of
$\leq $
-maximal elements of
![]() $\Psi ^+_1 \ \cup \ \Psi ^+_2$
, respectively. This implies that
$\Psi ^+_1 \ \cup \ \Psi ^+_2$
, respectively. This implies that
![]() $\Psi ^+_1$
is a crossing and that
$\Psi ^+_1$
is a crossing and that
![]() $\Psi ^+_2$
is a nesting, and it also follows that none of
$\Psi ^+_2$
is a nesting, and it also follows that none of
![]() $\Psi ^+_1, \Psi ^+_2$
and
$\Psi ^+_1, \Psi ^+_2$
and
![]() $\Psi ^+_3$
is both a crossing and a nesting. The quadruple Q must be one of
$\Psi ^+_3$
is both a crossing and a nesting. The quadruple Q must be one of
![]() $\Psi ^+_1, \Psi ^+_2$
and
$\Psi ^+_1, \Psi ^+_2$
and
![]() $\Psi ^+_3$
, and (ii) follows.
$\Psi ^+_3$
, and (ii) follows.
Part (iii) follows from (ii) since each of
![]() $\Psi ^+_C, \Psi ^+_N$
and
$\Psi ^+_C, \Psi ^+_N$
and
![]() $\Psi ^+_A$
uniquely determines
$\Psi ^+_A$
uniquely determines
![]() $\Psi ^+$
as its associated
$\Psi ^+$
as its associated
![]() $D_4$
-subsystem by Proposition 3.3 (iii).
$D_4$
-subsystem by Proposition 3.3 (iii).
Part (iv) holds as each of the quadruples in
![]() $\{\Psi ^+_C, \Psi ^+_N, \Psi ^+_A\}$
is a basis for the span of
$\{\Psi ^+_C, \Psi ^+_N, \Psi ^+_A\}$
is a basis for the span of
![]() $\Psi ^+$
, so that any root that is orthogonal to every element of one quadruple is also orthogonal to every element of each of the other quadruples.
$\Psi ^+$
, so that any root that is orthogonal to every element of one quadruple is also orthogonal to every element of each of the other quadruples.
Finally, the claims in (v) and (vi) can all be verified by inspection or direct computation based on the description of
![]() $\Psi ^+_C=\Psi ^+_1, \Psi ^+_N=\Psi ^+_2$
and
$\Psi ^+_C=\Psi ^+_1, \Psi ^+_N=\Psi ^+_2$
and
![]() $\Psi ^+_A=\Psi ^+_3$
. For the equation
$\Psi ^+_A=\Psi ^+_3$
. For the equation
![]() $\gamma _C=\gamma _N+\gamma _A$
and the assertion about
$\gamma _C=\gamma _N+\gamma _A$
and the assertion about
![]() $s_\alpha $
in (vi), one can alternatively prove them using the usual realizations of the root system and Weyl group of type
$s_\alpha $
in (vi), one can alternatively prove them using the usual realizations of the root system and Weyl group of type
![]() $D_4$
, where the simple roots are
$D_4$
, where the simple roots are
![]() $\alpha _1 = \varepsilon _1 - \varepsilon _2$
,
$\alpha _1 = \varepsilon _1 - \varepsilon _2$
,
![]() $\alpha _2 = \varepsilon _2 - \varepsilon _3$
,
$\alpha _2 = \varepsilon _2 - \varepsilon _3$
,
![]() $\alpha _3 = \varepsilon _3 - \varepsilon _4$
and
$\alpha _3 = \varepsilon _3 - \varepsilon _4$
and
![]() $\alpha _4 = \varepsilon _3 + \varepsilon _4$
and the group W acts as signed permutations. Under this realization, we have
$\alpha _4 = \varepsilon _3 + \varepsilon _4$
and the group W acts as signed permutations. Under this realization, we have
and the equation
![]() $\gamma _C=\gamma _N+\gamma _A$
follows as the terms expressed in coordinates satisfy the Ptolemy relation
$\gamma _C=\gamma _N+\gamma _A$
follows as the terms expressed in coordinates satisfy the Ptolemy relation
Remark 3.11. In the setting of Theorem 3.10, the coordinate forms of the
![]() $4$
-roots
$4$
-roots
![]() $\gamma _C, \gamma _N, \gamma _A$
given in Equation (3.1) correspond via the bijection of Lemma 3.1 (ii) to the perfect matchings of the set
$\gamma _C, \gamma _N, \gamma _A$
given in Equation (3.1) correspond via the bijection of Lemma 3.1 (ii) to the perfect matchings of the set
![]() $[4]$
given by the crossing
$[4]$
given by the crossing
![]() $m_C=\{\{1,3\}, \{2,4\}\}$
, the nesting
$m_C=\{\{1,3\}, \{2,4\}\}$
, the nesting
![]() $m_N=\{\{1,4\},\{2,3\}\},$
and the alignment
$m_N=\{\{1,4\},\{2,3\}\},$
and the alignment
![]() $m_A=\{\{1,2\}, \{3,4\}\}$
, respectively. Definition 3.9 generalizes the notion of crossings, nestings and alignments in the sense that a coplanar quadruple in the sense of the definition is a crossing, nesting or alignment if and only if the corresponding perfect matching of the set
$m_A=\{\{1,2\}, \{3,4\}\}$
, respectively. Definition 3.9 generalizes the notion of crossings, nestings and alignments in the sense that a coplanar quadruple in the sense of the definition is a crossing, nesting or alignment if and only if the corresponding perfect matching of the set
![]() $[4]$
is a crossing, nesting or alignment, respectively, in the context of matchings.
$[4]$
is a crossing, nesting or alignment, respectively, in the context of matchings.
Remark 3.12. Let R be a maximal orthogonal set of positive roots and let
![]() $\alpha $
be a positive root not in R. Proposition 3.8 shows that the reflection
$\alpha $
be a positive root not in R. Proposition 3.8 shows that the reflection
![]() $s_\alpha $
changes precisely four elements in R which form a coplanar quadruple Q and that
$s_\alpha $
changes precisely four elements in R which form a coplanar quadruple Q and that
![]() $Q'=s_\alpha (Q)$
is another coplanar quadruple with the same associated
$Q'=s_\alpha (Q)$
is another coplanar quadruple with the same associated
![]() $D_4$
-subsystem as Q. Theorem 3.10 (vi) reveals more about
$D_4$
-subsystem as Q. Theorem 3.10 (vi) reveals more about
![]() $\alpha ,Q$
and
$\alpha ,Q$
and
![]() $Q'$
: it shows that Q and
$Q'$
: it shows that Q and
![]() $Q'$
are two distinct features from the set
$Q'$
are two distinct features from the set
![]() $\{\Psi ^+_C,\Psi ^+_N,\Psi ^+_A\}$
inside the
$\{\Psi ^+_C,\Psi ^+_N,\Psi ^+_A\}$
inside the
![]() $D_4$
-subsystem
$D_4$
-subsystem
![]() $\Psi $
associated to Q, while
$\Psi $
associated to Q, while
![]() $\alpha $
is in the remaining feature. We will say that
$\alpha $
is in the remaining feature. We will say that
![]() $s_\alpha $
moves Q in this case; we will also say that
$s_\alpha $
moves Q in this case; we will also say that
![]() $s_\alpha $
(or
$s_\alpha $
(or
![]() $\alpha $
) moves an X to a Y and call
$\alpha $
) moves an X to a Y and call
![]() $s_\alpha $
an XY move, where X and Y are the distinct types of Q and
$s_\alpha $
an XY move, where X and Y are the distinct types of Q and
![]() $Q'$
, respectively. Note that knowledge of Q and Y is enough to determine
$Q'$
, respectively. Note that knowledge of Q and Y is enough to determine
![]() $Q'$
by Theorem 3.10 (iii), even if
$Q'$
by Theorem 3.10 (iii), even if
![]() $\alpha $
is not known. Note also that Theorem 3.10 (vi) guarantees that
$\alpha $
is not known. Note also that Theorem 3.10 (vi) guarantees that
![]() $XY$
moves exist for any distinct elements X, Y in
$XY$
moves exist for any distinct elements X, Y in
![]() $\{C,N,A\}$
, so any two coplanar quadruples sharing the same
$\{C,N,A\}$
, so any two coplanar quadruples sharing the same
![]() $D_4$
-subsystem can be connected, up to sign, by a reflection.
$D_4$
-subsystem can be connected, up to sign, by a reflection.
The next proposition shows how to distinguish crossings, nestings and alignments from each other using only the heights of their components. Recall from Section 2.2 that in a root system with simple system
![]() $\{\alpha _1,\alpha _2, \cdots ,\alpha _n\}$
, the height of each root
$\{\alpha _1,\alpha _2, \cdots ,\alpha _n\}$
, the height of each root
![]() $\alpha =\sum _{i=1}^n c_i\alpha _i$
is the integer
$\alpha =\sum _{i=1}^n c_i\alpha _i$
is the integer
![]() $\textrm {ht}(\alpha )=\sum _{i=1}^n c_i$
.
$\textrm {ht}(\alpha )=\sum _{i=1}^n c_i$
.
Proposition 3.13. Let W be a Weyl group of type
![]() $E_7$
,
$E_7$
,
![]() $E_8$
or
$E_8$
or
![]() $D_n$
for n even. Let
$D_n$
for n even. Let
![]() $Q = \{\beta _1, \beta _2, \beta _3, \beta _4\}$
be a coplanar quadruple of orthogonal positive roots, ordered so that we have
$Q = \{\beta _1, \beta _2, \beta _3, \beta _4\}$
be a coplanar quadruple of orthogonal positive roots, ordered so that we have
![]() $h_1 \leq h_2 \leq h_3 \leq h_4$
where
$h_1 \leq h_2 \leq h_3 \leq h_4$
where
![]() $h_i=\textrm {ht}(\beta _i)$
for each i.
$h_i=\textrm {ht}(\beta _i)$
for each i.
-
(i) We have
 $h_1 + h_2 + h_3 \ne h_4$
and
$h_1 + h_2 + h_3 \ne h_4$
and
 $h_2 + h_3 \ne h_1 + h_4$
.
$h_2 + h_3 \ne h_1 + h_4$
. -
(ii) If
 $h_1 + h_2 + h_3 < h_4$
, then Q is an alignment.
$h_1 + h_2 + h_3 < h_4$
, then Q is an alignment. -
(iii) If
 $h_1 + h_2 + h_3> h_4$
and
$h_1 + h_2 + h_3> h_4$
and
 $h_2 + h_3> h_1 + h_4$
, then Q is a nesting. In this case, we also have
$h_2 + h_3> h_1 + h_4$
, then Q is a nesting. In this case, we also have
 $h_1 < h_2$
.
$h_1 < h_2$
. -
(iv) If
 $h_1 + h_2 + h_3> h_4$
and
$h_1 + h_2 + h_3> h_4$
and
 $h_2 + h_3 < h_1 + h_4$
, then Q is a crossing. In this case, we also have
$h_2 + h_3 < h_1 + h_4$
, then Q is a crossing. In this case, we also have
 $h_1> 1$
and
$h_1> 1$
and
 $h_3 < h_4$
.
$h_3 < h_4$
.
Proof. Let
![]() $\Psi $
be the type
$\Psi $
be the type
![]() $D_4$
subsystem associated to Q, and let
$D_4$
subsystem associated to Q, and let
![]() $\{\alpha _1, \alpha _2, \alpha _3, \alpha _4\}$
be the simple system of
$\{\alpha _1, \alpha _2, \alpha _3, \alpha _4\}$
be the simple system of
![]() $\Psi $
induced by
$\Psi $
induced by
![]() $\Phi ^+$
, with
$\Phi ^+$
, with
![]() $\alpha _2$
corresponding to the branch node in the Dynkin diagram. Then as in the proof of Theorem 3.10, the set
$\alpha _2$
corresponding to the branch node in the Dynkin diagram. Then as in the proof of Theorem 3.10, the set
![]() $\Psi ^+$
decomposes into the union of the crossing
$\Psi ^+$
decomposes into the union of the crossing
![]() $\Psi ^+_C$
, nesting
$\Psi ^+_C$
, nesting
![]() $\Psi ^+_N$
and alignment
$\Psi ^+_N$
and alignment
![]() $\Psi ^+_A$
given below:
$\Psi ^+_A$
given below:
If
![]() $Q=\Psi ^+_A$
, then we have
$Q=\Psi ^+_A$
, then we have
![]() $\beta _4 - \beta _1 - \beta _2 - \beta _3 = 2\alpha _2$
, and
$\beta _4 - \beta _1 - \beta _2 - \beta _3 = 2\alpha _2$
, and
![]() $\beta _4 + \beta _1 - \beta _2 - \beta _3 = 2\alpha _2 + 2\alpha _i$
for some
$\beta _4 + \beta _1 - \beta _2 - \beta _3 = 2\alpha _2 + 2\alpha _i$
for some
![]() $i \in \{1, 3, 4\}$
.
$i \in \{1, 3, 4\}$
.
If
![]() $Q=\Psi ^+_N$
, then we have
$Q=\Psi ^+_N$
, then we have
![]() $\beta _1 < \beta _j$
for all
$\beta _1 < \beta _j$
for all
![]() $j \in \{2, 3, 4\}$
. We also have
$j \in \{2, 3, 4\}$
. We also have
![]() $\beta _4 - \beta _1 - \beta _2 - \beta _3 = -2\alpha _i - 2\alpha _2$
for some
$\beta _4 - \beta _1 - \beta _2 - \beta _3 = -2\alpha _i - 2\alpha _2$
for some
![]() $i \in \{1, 3, 4\}$
, and
$i \in \{1, 3, 4\}$
, and
![]() $\beta _4 + \beta _1 - \beta _2 - \beta _3 = -2\alpha _i$
for some
$\beta _4 + \beta _1 - \beta _2 - \beta _3 = -2\alpha _i$
for some
![]() $i \in \{1, 3, 4\}$
.
$i \in \{1, 3, 4\}$
.
If
![]() $Q=\Psi ^+_C$
, then we have
$Q=\Psi ^+_C$
, then we have
![]() $\beta _4> \beta _j$
for all
$\beta _4> \beta _j$
for all
![]() $j \in \{1, 2, 3\}$
. We also have
$j \in \{1, 2, 3\}$
. We also have
![]() $\beta _4 - \beta _1 - \beta _2 - \beta _3 = -2\alpha _2$
and
$\beta _4 - \beta _1 - \beta _2 - \beta _3 = -2\alpha _2$
and
![]() $\beta _4 + \beta _1 - \beta _2 - \beta _3 = 2\alpha _i$
for some
$\beta _4 + \beta _1 - \beta _2 - \beta _3 = 2\alpha _i$
for some
![]() $i \in \{1, 3, 4\}$
. Furthermore, none of the
$i \in \{1, 3, 4\}$
. Furthermore, none of the
![]() $\beta _i$
is a simple root of
$\beta _i$
is a simple root of
![]() $\Phi $
because none of the
$\Phi $
because none of the
![]() $\beta _i$
is even a simple root of
$\beta _i$
is even a simple root of
![]() $\Psi $
.
$\Psi $
.
All the claims in the proposition follow from the above observations. Note that the conditions in (ii), (iii), and (iv) are exclusive and exhaustive because of part (i).
Remark 3.14. It can be shown that if W is a Weyl group of type
![]() $E_7, E_8$
or
$E_7, E_8$
or
![]() $D_n$
for n even and the components of a positive n-root
$D_n$
for n even and the components of a positive n-root
![]() $\beta $
have heights
$\beta $
have heights
![]() $h_1, h_2, \ldots , h_n$
, then the number
$h_1, h_2, \ldots , h_n$
, then the number
![]() $\sum _{i = 1}^n h_i^2$
depends only on W and is independent of the choice of
$\sum _{i = 1}^n h_i^2$
depends only on W and is independent of the choice of
![]() $\beta $
.
$\beta $
.
3.3 Intersections of coplanar quadruples
Let R be a maximal orthogonal set of roots of W. In this subsection, we first focus on type
![]() $E_8$
and show that coplanar quadruples in R gives rise to a Steiner quadruple system in this type. We will then use this result to count coplanar quadruples in R and deduce how coplanar quadruples in R can overlap with each other, in the general case.
$E_8$
and show that coplanar quadruples in R gives rise to a Steiner quadruple system in this type. We will then use this result to count coplanar quadruples in R and deduce how coplanar quadruples in R can overlap with each other, in the general case.
Definition 3.15. A Steiner system
![]() $S(t,k,N)$
is a collection B of k-element subsets of the set
$S(t,k,N)$
is a collection B of k-element subsets of the set
![]() $[N]=\{1,2,\dots , N\}$
with the property that every t-element subset is contained in a unique element of B. The elements of B are called blocks, and we write each block
$[N]=\{1,2,\dots , N\}$
with the property that every t-element subset is contained in a unique element of B. The elements of B are called blocks, and we write each block
![]() $\{a,b,c,\dots \}$
where
$\{a,b,c,\dots \}$
where
![]() $a<b<c<\dots $
as
$a<b<c<\dots $
as
![]() $abc\dots $
. We call B a Steiner triple system if
$abc\dots $
. We call B a Steiner triple system if
![]() $k=3$
and a Steiner quadruple system if
$k=3$
and a Steiner quadruple system if
![]() $k=4$
.
$k=4$
.
Remark 3.16. A Steiner system
![]() $S(t,k,N)$
is also known as a t-
$S(t,k,N)$
is also known as a t-
![]() $(N,k,1)$
design, which is a special kind of t-designs [Reference Colbourn and Dinitz18, Section 4.1]. It is well known that, up to isomorphism (by permutations), there is a unique Steiner triple system
$(N,k,1)$
design, which is a special kind of t-designs [Reference Colbourn and Dinitz18, Section 4.1]. It is well known that, up to isomorphism (by permutations), there is a unique Steiner triple system
![]() $S(2,3,7)$
and a unique Steiner quadruple system
$S(2,3,7)$
and a unique Steiner quadruple system
![]() $S(3,4,8)$
[Reference Barrau4]. The following 14 quadruples form an example of a Steiner quadruple system, and removing the element 8 from all the quadruples on the left results in a Steiner triple system.
$S(3,4,8)$
[Reference Barrau4]. The following 14 quadruples form an example of a Steiner quadruple system, and removing the element 8 from all the quadruples on the left results in a Steiner triple system.
 $$ \begin{align*} \begin{array}{cc} \displaystyle 1\ 2\ 4\ 8 \quad& \quad \displaystyle 3\ 5\ 6\ 7 \\ \displaystyle 2\ 3\ 5\ 8 \quad &\quad \displaystyle 1\ 4\ 6\ 7 \\ \displaystyle 3\ 4\ 6\ 8 \quad& \quad \displaystyle 1\ 2\ 5\ 7 \\ \displaystyle 4\ 5\ 7\ 8 \quad& \quad \displaystyle 1\ 2\ 3\ 6 \\ \displaystyle 1\ 5\ 6\ 8 \quad& \quad \displaystyle 2\ 3\ 4\ 7 \\ \displaystyle 2\ 6\ 7\ 8 \quad& \quad \displaystyle 1\ 3\ 4\ 5 \\ \displaystyle 1\ 3\ 7\ 8 \quad& \quad \displaystyle 2\ 4\ 5\ 6 \\ \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{cc} \displaystyle 1\ 2\ 4\ 8 \quad& \quad \displaystyle 3\ 5\ 6\ 7 \\ \displaystyle 2\ 3\ 5\ 8 \quad &\quad \displaystyle 1\ 4\ 6\ 7 \\ \displaystyle 3\ 4\ 6\ 8 \quad& \quad \displaystyle 1\ 2\ 5\ 7 \\ \displaystyle 4\ 5\ 7\ 8 \quad& \quad \displaystyle 1\ 2\ 3\ 6 \\ \displaystyle 1\ 5\ 6\ 8 \quad& \quad \displaystyle 2\ 3\ 4\ 7 \\ \displaystyle 2\ 6\ 7\ 8 \quad& \quad \displaystyle 1\ 3\ 4\ 5 \\ \displaystyle 1\ 3\ 7\ 8 \quad& \quad \displaystyle 2\ 4\ 5\ 6 \\ \end{array} \end{align*} $$
Lemma 3.17. Let
![]() $\beta _1, \beta _2, \beta _3$
be three mutually orthogonal positive roots of type
$\beta _1, \beta _2, \beta _3$
be three mutually orthogonal positive roots of type
![]() $E_8$
.
$E_8$
.
-
(i) There exists a unique positive root
 $\beta _4$
such that
$\beta _4$
such that
 $\{\beta _1, \beta _2, \beta _3, \beta _4\}$
is a coplanar quadruple.
$\{\beta _1, \beta _2, \beta _3, \beta _4\}$
is a coplanar quadruple. -
(ii) If R is a maximal orthogonal set of positive roots of type
 $E_8$
, and
$E_8$
, and
 $\{\beta _1, \beta _2, \beta _3\} \subset R$
, then we have
$\{\beta _1, \beta _2, \beta _3\} \subset R$
, then we have
 $\beta _4 \in R$
.
$\beta _4 \in R$
.
Proof. By [Reference Carter11, Lemma 11 (iii)] and its proof, if
![]() $W = W(E_8)$
, then W acts transitively on ordered triples of orthogonal roots, and the set of roots orthogonal to three given mutually orthogonal roots is a root system of type
$W = W(E_8)$
, then W acts transitively on ordered triples of orthogonal roots, and the set of roots orthogonal to three given mutually orthogonal roots is a root system of type
![]() $A_1 + D_4$
. Since the action of orthogonal triples of roots is transitive, it suffices to prove (i) for a fixed choice of
$A_1 + D_4$
. Since the action of orthogonal triples of roots is transitive, it suffices to prove (i) for a fixed choice of
![]() $\beta _1$
,
$\beta _1$
,
![]() $\beta _2$
and
$\beta _2$
and
![]() $\beta _3$
. If we choose
$\beta _3$
. If we choose
![]() $\beta _1 = \alpha _3 = 2(\varepsilon _2 - \varepsilon _1)$
,
$\beta _1 = \alpha _3 = 2(\varepsilon _2 - \varepsilon _1)$
,
![]() $\beta _2 = \alpha _5 = 2(\varepsilon _4 - \varepsilon _3)$
and
$\beta _2 = \alpha _5 = 2(\varepsilon _4 - \varepsilon _3)$
and
![]() $\beta _3 = \alpha _7 = 2(\varepsilon _6 - \varepsilon _5)$
, then it follows from the explicit description of the root system in Section 2.3 that the only positive root that forms a coplanar quadruple with
$\beta _3 = \alpha _7 = 2(\varepsilon _6 - \varepsilon _5)$
, then it follows from the explicit description of the root system in Section 2.3 that the only positive root that forms a coplanar quadruple with
![]() $\beta _1,\beta _2$
and
$\beta _1,\beta _2$
and
![]() $\beta _3$
is the root
$\beta _3$
is the root
![]() $\beta _4 = 2(\varepsilon _8 - \varepsilon _7)$
. This proves (i).
$\beta _4 = 2(\varepsilon _8 - \varepsilon _7)$
. This proves (i).
The uniqueness property of (i) proves that the set of coplanar quadruples corresponds to the
![]() $A_1$
summand of the
$A_1$
summand of the
![]() $A_1 + D_4$
subsystem. This implies that if
$A_1 + D_4$
subsystem. This implies that if
![]() $\beta $
is any positive root that is orthogonal to all of
$\beta $
is any positive root that is orthogonal to all of
![]() $\beta _1$
,
$\beta _1$
,
![]() $\beta _2$
and
$\beta _2$
and
![]() $\beta _3$
, then either
$\beta _3$
, then either
![]() $\beta _4 = \beta $
, or
$\beta _4 = \beta $
, or
![]() $\beta _4$
is orthogonal to
$\beta _4$
is orthogonal to
![]() $\beta $
. The maximality of R in the statement of (ii) implies that
$\beta $
. The maximality of R in the statement of (ii) implies that
![]() $\beta _4$
cannot be orthogonal to all elements of R. It follows that
$\beta _4$
cannot be orthogonal to all elements of R. It follows that
![]() $\beta _4 \in R$
, which proves (ii).
$\beta _4 \in R$
, which proves (ii).
Lemma 3.18. Let W be a Weyl group of type
![]() $E_8$
, and let R be a maximal orthogonal set of roots.
$E_8$
, and let R be a maximal orthogonal set of roots.
-
(i) The coplanar quadruples of R endow R with the structure of a Steiner quadruple system
 $S(3,4,8)$
.
$S(3,4,8)$
. -
(ii) Any two coplanar quadruples of R intersect in either
 $0$
,
$0$
,
 $2$
, or
$2$
, or
 $4$
elements.
$4$
elements.
Proof. Part (i) is immediate from Lemma 3.17. To prove part (ii), we need to show that any two distinct quadruples from the Steiner quadruple system are either disjoint or overlap in precisely two elements. This can be proved by an exhaustive check, or by arguing as follows.
The quadruples in the left column of the table consist of the element 8 together with three points forming a line in the Fano plane (see Section 6.2). Any two such quadruples intersect in two elements: the element 8 and the unique point on the intersection of the two lines of the Fano plane. The general case follows by combining this observation with the fact that each quadruple in the right column is the complement of the corresponding quadruple in the left column.
Corollary 3.19. Let W be a Weyl group of type
![]() $E_7$
,
$E_7$
,
![]() $E_8$
or
$E_8$
or
![]() $D_n$
for n even and
$D_n$
for n even and
![]() $n=2k\ge 4$
. Let R be a maximal orthogonal set of positive roots. Then the number M of coplanar quadruples contained in R does not depend on R. We have
$n=2k\ge 4$
. Let R be a maximal orthogonal set of positive roots. Then the number M of coplanar quadruples contained in R does not depend on R. We have
![]() $M = \binom {k}{2}$
if W has type
$M = \binom {k}{2}$
if W has type
![]() $D_{2k}$
,
$D_{2k}$
,
![]() $M = 7$
if W has type
$M = 7$
if W has type
![]() $E_7$
, and
$E_7$
, and
![]() $M = 14$
if W has type
$M = 14$
if W has type
![]() $E_8$
.
$E_8$
.
Proof. If W has type
![]() $D_{2k}$
, then R determines a perfect matching of the set
$D_{2k}$
, then R determines a perfect matching of the set
![]() $\{1, 2, \ldots , 2k\}$
with k blocks by Lemma 3.1, and the coplanar quadruples in R correspond bijectively to pairs of these blocks by Remark 3.6. It follows that M does not depend on R and equals
$\{1, 2, \ldots , 2k\}$
with k blocks by Lemma 3.1, and the coplanar quadruples in R correspond bijectively to pairs of these blocks by Remark 3.6. It follows that M does not depend on R and equals
![]() $\binom {k}{2}$
.
$\binom {k}{2}$
.
In type
![]() $E_8$
, the result follows from Lemma 3.18 (i).
$E_8$
, the result follows from Lemma 3.18 (i).
If W has type
![]() $E_7$
, then as in the proof of Proposition 3.8, we may again identify the root system of W with the set of roots orthogonal to the the highest root
$E_7$
, then as in the proof of Proposition 3.8, we may again identify the root system of W with the set of roots orthogonal to the the highest root
![]() $\theta $
in the root system of type
$\theta $
in the root system of type
![]() $E_8$
. The set
$E_8$
. The set
![]() $R \cup \{\theta \}$
is then a maximal orthogonal set of roots in type
$R \cup \{\theta \}$
is then a maximal orthogonal set of roots in type
![]() $E_8$
. The coplanar quadruples of R are in bijection with the quadruples of
$E_8$
. The coplanar quadruples of R are in bijection with the quadruples of
![]() $S(3,4,8)$
that exclude a fixed element, and there are
$S(3,4,8)$
that exclude a fixed element, and there are
![]() $7$
such quadruples, so we are done.
$7$
such quadruples, so we are done.
Proposition 3.20. Let W be a Weyl group of type
![]() $E_7$
,
$E_7$
,
![]() $E_8$
or
$E_8$
or
![]() $D_n$
for n even. Let R be a maximal orthogonal subset of positive roots, and suppose
$D_n$
for n even. Let R be a maximal orthogonal subset of positive roots, and suppose
![]() $Q_1$
and
$Q_1$
and
![]() $Q_2$
are coplanar quadruples of roots contained in R.
$Q_2$
are coplanar quadruples of roots contained in R.
-
(i) The intersection
 $Q_1 \cap Q_2$
has size 0, 2 or 4.
$Q_1 \cap Q_2$
has size 0, 2 or 4. -
(ii) If
 $|Q_1 \cap Q_2| = 2$
, then there is a root subsystem
$|Q_1 \cap Q_2| = 2$
, then there is a root subsystem
 $\Psi \subseteq \Phi $
of type
$\Psi \subseteq \Phi $
of type
 $D_6$
that contains both
$D_6$
that contains both
 $Q_1$
and
$Q_1$
and
 $Q_2$
. In this case, each of the sets
$Q_2$
. In this case, each of the sets
 $Q_1$
,
$Q_1$
,
 $Q_2$
,
$Q_2$
,
 $Q_1 \cap Q_2$
, and
$Q_1 \cap Q_2$
, and
 $Q_1 \cup Q_2$
consists of collinear pairs of roots with respect to
$Q_1 \cup Q_2$
consists of collinear pairs of roots with respect to
 $\Psi $
, and the symmetric difference
$\Psi $
, and the symmetric difference
 $Q_1 \ \Delta \ Q_2$
is also a coplanar quadruple.
$Q_1 \ \Delta \ Q_2$
is also a coplanar quadruple.
Proof. If W has type
![]() $D_n$
, then the assertions follow from Lemma 3.5.
$D_n$
, then the assertions follow from Lemma 3.5.
Suppose that W has type
![]() $E_8$
. In this case, part (i) follows from Lemma 3.18 (ii). If
$E_8$
. In this case, part (i) follows from Lemma 3.18 (ii). If
![]() $|Q_1 \cap Q_2| = 2$
, then
$|Q_1 \cap Q_2| = 2$
, then
![]() $|Q_1 \cup Q_2| = 6$
, and there are precisely two elements
$|Q_1 \cup Q_2| = 6$
, and there are precisely two elements
![]() $\alpha , \beta \in R$
that are orthogonal to every root in
$\alpha , \beta \in R$
that are orthogonal to every root in
![]() $Q_1 \cup Q_2$
. Let
$Q_1 \cup Q_2$
. Let
![]() $\Psi $
be the set of roots in
$\Psi $
be the set of roots in
![]() $\Phi $
that are orthogonal to
$\Phi $
that are orthogonal to
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
. Then
$\beta $
. Then
![]() $\Psi $
forms a root system of type
$\Psi $
forms a root system of type
![]() $D_6$
by Section 2.3, proving the first assertion of (ii), and the sets
$D_6$
by Section 2.3, proving the first assertion of (ii), and the sets
![]() $Q_1, Q_2, Q_1\cap Q_2$
and
$Q_1, Q_2, Q_1\cap Q_2$
and
![]() $Q_1\cup Q_2$
all lie in
$Q_1\cup Q_2$
all lie in
![]() $\Psi $
. The other assertions of (ii) now follow by applying the type
$\Psi $
. The other assertions of (ii) now follow by applying the type
![]() $D_n$
case of the result to
$D_n$
case of the result to
![]() $\Psi $
.
$\Psi $
.
Finally, suppose that W has type
![]() $E_7$
. We identify the root system with the set of roots orthogonal to the the highest root
$E_7$
. We identify the root system with the set of roots orthogonal to the the highest root
![]() $\theta $
in the root system of type
$\theta $
in the root system of type
![]() $E_8$
as usual. Then
$E_8$
as usual. Then
![]() $R \cup \{\theta \}$
is a maximal orthogonal set of roots in type
$R \cup \{\theta \}$
is a maximal orthogonal set of roots in type
![]() $E_8$
. The assertions in this case follow by applying the argument of the previous paragraph with
$E_8$
. The assertions in this case follow by applying the argument of the previous paragraph with
![]() $\alpha = \theta $
.
$\alpha = \theta $
.
4 Quasiparabolic structure
Let
![]() $X=X(W)$
be the set of all maximal orthogonal sets of positive roots of W, and recall from the introduction that W acts on X naturally via the action
$X=X(W)$
be the set of all maximal orthogonal sets of positive roots of W, and recall from the introduction that W acts on X naturally via the action
![]() $w(\{\beta _1,\cdots ,\beta _n\})=\{\lvert w(\beta _1) \rvert , \cdots , \lvert w(\beta _n) \rvert \}$
. In this section, we recall the notion of a quasiparabolic set as defined by Rains and Vazirani [Reference Rains and Vazirani43], and we use the concepts of crossings and nestings to endow the W-set X with a quasiparabolic structure.
$w(\{\beta _1,\cdots ,\beta _n\})=\{\lvert w(\beta _1) \rvert , \cdots , \lvert w(\beta _n) \rvert \}$
. In this section, we recall the notion of a quasiparabolic set as defined by Rains and Vazirani [Reference Rains and Vazirani43], and we use the concepts of crossings and nestings to endow the W-set X with a quasiparabolic structure.
4.1 Quasiparabolic sets
Quasiparabolic sets were introduced by Rains and Vazirani for a general Coxeter system as follows.
Definition 4.1 [Reference Rains and Vazirani43, Section 2, Section 5]. Let W be a Coxeter group with generating set S and set of reflections T. A scaled W-set is a pair
![]() $(\mathcal {X}, \lambda )$
, where
$(\mathcal {X}, \lambda )$
, where
![]() $\mathcal {X}$
is a W-set and
$\mathcal {X}$
is a W-set and
![]() $\lambda : \mathcal {X} \rightarrow {\mathbb Z}$
is a function satisfying
$\lambda : \mathcal {X} \rightarrow {\mathbb Z}$
is a function satisfying
![]() $|\lambda (sx) - \lambda (x)| \leq 1$
for all
$|\lambda (sx) - \lambda (x)| \leq 1$
for all
![]() $s \in S$
. An element
$s \in S$
. An element
![]() $x \in \mathcal {X}$
is W-minimal if
$x \in \mathcal {X}$
is W-minimal if
![]() $\lambda (sx) \geq \lambda (x)$
and is W-maximal if
$\lambda (sx) \geq \lambda (x)$
and is W-maximal if
![]() $\lambda (sx) \leq \lambda (x)$
for all
$\lambda (sx) \leq \lambda (x)$
for all
![]() $s \in S$
.
$s \in S$
.
A quasiparabolic set for W is a scaled W-set
![]() $\mathcal {X}$
satisfying the following two properties:
$\mathcal {X}$
satisfying the following two properties:
-
(QP1) for any
 $r \in T$
and
$r \in T$
and
 $x \in \mathcal {X}$
, if
$x \in \mathcal {X}$
, if
 $\lambda (rx) = \lambda (x)$
, then
$\lambda (rx) = \lambda (x)$
, then
 $rx = x$
;
$rx = x$
; -
(QP2) for any
 $r \in T$
,
$r \in T$
,
 $x \in \mathcal {X}$
, and
$x \in \mathcal {X}$
, and
 $s \in S$
, if
$s \in S$
, if
 $\lambda (rx)> \lambda (x)$
and
$\lambda (rx)> \lambda (x)$
and
 $\lambda (srx) < \lambda (sx)$
, then
$\lambda (srx) < \lambda (sx)$
, then
 $rx = sx$
.
$rx = sx$
.
For a quasiparabolic set
![]() $\mathcal {X}$
, we define
$\mathcal {X}$
, we define
![]() $\le _Q$
to be the weakest partial order such that
$\le _Q$
to be the weakest partial order such that
![]() $x \leq _Q rx$
whenever
$x \leq _Q rx$
whenever
![]() $x \in \mathcal {X}$
,
$x \in \mathcal {X}$
,
![]() $r \in T$
, and
$r \in T$
, and
![]() $\lambda (x) \leq \lambda (rx)$
.
$\lambda (x) \leq \lambda (rx)$
.
Rains and Vazirani call
![]() $\lambda (x)$
the height of x, and
$\lambda (x)$
the height of x, and
![]() $\leq _Q$
the Bruhat order, but we will refer to them as the level of x and the quasiparabolic order because of the potential for confusion in the context of this paper. It follows from [Reference Rains and Vazirani43, Proposition 5.16] that
$\leq _Q$
the Bruhat order, but we will refer to them as the level of x and the quasiparabolic order because of the potential for confusion in the context of this paper. It follows from [Reference Rains and Vazirani43, Proposition 5.16] that
![]() $\lambda $
is a rank function with respect to the partial order
$\lambda $
is a rank function with respect to the partial order
![]() $\leq _Q$
, so that every covering relation
$\leq _Q$
, so that every covering relation
![]() $x <_Q y$
satisfies
$x <_Q y$
satisfies
![]() $\lambda (y) = \lambda (x) + 1$
.
$\lambda (y) = \lambda (x) + 1$
.
We will show that the set
![]() $X=X(W)$
forms a quasiparabolic set for the Weyl group W in type
$X=X(W)$
forms a quasiparabolic set for the Weyl group W in type
![]() $E_7, E_8$
or
$E_7, E_8$
or
![]() $D_{n}$
with n even under a suitable level function defined in terms of coplanar quadruples. We define the level function and some other useful statistics below.
$D_{n}$
with n even under a suitable level function defined in terms of coplanar quadruples. We define the level function and some other useful statistics below.
Definition 4.2. Let W be a Weyl group of type
![]() $E_7, E_8$
or
$E_7, E_8$
or
![]() $D_{n}$
for n even. Let R be a set of mutually orthogonal roots of W, and let
$D_{n}$
for n even. Let R be a set of mutually orthogonal roots of W, and let
![]() $\beta $
be a positive n-root of W.
$\beta $
be a positive n-root of W.
-
(i) We define the crossing number
 $C(R)$
, the nesting number
$C(R)$
, the nesting number
 $N(R)$
and the alignment number
$N(R)$
and the alignment number
 $A(R)$
of R to be the numbers of crossings, nestings and alignments contained in
$A(R)$
of R to be the numbers of crossings, nestings and alignments contained in
 $R^+$
, respectively.
$R^+$
, respectively. -
(ii) We define the type of R to be the monomial
 $A^{A(R)}C^{C(R)}N^{N(R)}$
, and define the level
$A^{A(R)}C^{C(R)}N^{N(R)}$
, and define the level
 $\lambda (R)$
of R to be
$\lambda (R)$
of R to be
 $C(R) + 2N(R)$
.
$C(R) + 2N(R)$
. -
(iii) If R is a maximal orthogonal set of roots, then we say that R is noncrossing, nonnesting and alignment-free if
 $C(R)=0$
,
$C(R)=0$
,
 $N(R)=0$
and
$N(R)=0$
and
 $A(R)=0$
, respectively; we also call R maximally crossing, maximally nesting or maximally aligned if we have
$A(R)=0$
, respectively; we also call R maximally crossing, maximally nesting or maximally aligned if we have
 $N(R)=A(R)=0$
,
$N(R)=A(R)=0$
,
 $C(R)=A(R)=0$
or
$C(R)=A(R)=0$
or
 $C(R)=N(R)=0$
, respectively.
$C(R)=N(R)=0$
, respectively.
We also apply all the above definitions to
![]() $\beta $
by applying them to the set of components of
$\beta $
by applying them to the set of components of
![]() $\beta $
. (Note that the definitions of type in (ii) and in Definition 3.9 are consistent.)
$\beta $
. (Note that the definitions of type in (ii) and in Definition 3.9 are consistent.)
Remark 4.3. By Corollary 3.19, when R is a maximal orthogonal set of positive roots, the sum of the numbers
![]() $C(R), N(R)$
and
$C(R), N(R)$
and
![]() $A(R)$
is a constant depending only on W and not on R; therefore, each of these numbers achieves the maximal possible value when the other two equal zero. This justifies the terms ‘maximally crossing’, ‘maximally nesting’ and ‘maximally aligned’ in Definition 4.2.(iii).
$A(R)$
is a constant depending only on W and not on R; therefore, each of these numbers achieves the maximal possible value when the other two equal zero. This justifies the terms ‘maximally crossing’, ‘maximally nesting’ and ‘maximally aligned’ in Definition 4.2.(iii).
Example 4.4. Suppose that W has type
![]() $D_6$
, and that
$D_6$
, and that
![]() $R=\{\varepsilon _1 \pm \varepsilon _2,\varepsilon _3\pm \varepsilon _6,\varepsilon _4 \pm \varepsilon _5\}$
is the maximal orthogonal set of positive roots corresponding to the matching
$R=\{\varepsilon _1 \pm \varepsilon _2,\varepsilon _3\pm \varepsilon _6,\varepsilon _4 \pm \varepsilon _5\}$
is the maximal orthogonal set of positive roots corresponding to the matching
![]() $\{12,36,45\}$
(via the natural bijection of Lemma 3.1 (ii)). In this case, R contains two alignments, corresponding to the pairs
$\{12,36,45\}$
(via the natural bijection of Lemma 3.1 (ii)). In this case, R contains two alignments, corresponding to the pairs
![]() $\{12,45\}$
and
$\{12,45\}$
and
![]() $\{12, 36\}$
, and one nesting, corresponding to the pair
$\{12, 36\}$
, and one nesting, corresponding to the pair
![]() $\{36, 45\}$
. The type of R is therefore
$\{36, 45\}$
. The type of R is therefore
![]() $A^2 C^0 N^1$
(or
$A^2 C^0 N^1$
(or
![]() $AAN$
).
$AAN$
).
We now state the main theorem of this section. Its proof will occupy the next subsection.
Theorem 4.5. Let W be a Weyl group of type
![]() $E_7$
,
$E_7$
,
![]() $E_8$
or
$E_8$
or
![]() $D_n$
for n even, and let X be the set of maximal orthogonal sets of positive roots of W, regarded as a W-set under the action
$D_n$
for n even, and let X be the set of maximal orthogonal sets of positive roots of W, regarded as a W-set under the action
Then the set
![]() $(X, \lambda )$
is a quasiparabolic set for W, where
$(X, \lambda )$
is a quasiparabolic set for W, where
![]() $\lambda : X \rightarrow {\mathbb Z}$
is the level function
$\lambda : X \rightarrow {\mathbb Z}$
is the level function
![]() $\lambda (x) = C(x) + 2N(x)$
.
$\lambda (x) = C(x) + 2N(x)$
.
4.2 Proof of Theorem 4.5
We will prove Theorem 4.5 by showing that the set X is a scaled W-set satisfying the axioms (QP1) and (QP2) of Definition 4.1. To this end, we first study how the action of a reflection
![]() $s_\alpha $
corresponding to a root
$s_\alpha $
corresponding to a root
![]() $\alpha $
can affect the level of a maximal orthogonal set R of roots. Recall from Remark 3.12 that
$\alpha $
can affect the level of a maximal orthogonal set R of roots. Recall from Remark 3.12 that
![]() $s_\alpha $
must replace a coplanar quadruple in R with a feature of a different type whenever R does not contain
$s_\alpha $
must replace a coplanar quadruple in R with a feature of a different type whenever R does not contain
![]() $\pm \alpha $
. We will therefore examine how such feature replacements affect the level function
$\pm \alpha $
. We will therefore examine how such feature replacements affect the level function
![]() $\lambda $
. Also recall from Section 2 that the root system
$\lambda $
. Also recall from Section 2 that the root system
![]() $\Phi $
is equipped with a natural partial order
$\Phi $
is equipped with a natural partial order
![]() $\le $
defined by the condition that
$\le $
defined by the condition that
![]() $\alpha \le \beta $
if and only if
$\alpha \le \beta $
if and only if
![]() $\beta -\alpha $
is a nonnegative linear combination of simple roots. We will frequently use the order
$\beta -\alpha $
is a nonnegative linear combination of simple roots. We will frequently use the order
![]() $\le $
throughout the proofs.
$\le $
throughout the proofs.
Example 4.6. Let
![]() $W=W(D_6)$
and
$W=W(D_6)$
and
![]() $R=\{\varepsilon _1 \pm \varepsilon _2,\varepsilon _3\pm \varepsilon _6,\varepsilon _4 \pm \varepsilon _5\}$
be as in Example 4.4. Let
$R=\{\varepsilon _1 \pm \varepsilon _2,\varepsilon _3\pm \varepsilon _6,\varepsilon _4 \pm \varepsilon _5\}$
be as in Example 4.4. Let
![]() $\alpha = \varepsilon _2 - \varepsilon _4$
, so that
$\alpha = \varepsilon _2 - \varepsilon _4$
, so that
![]() $s_\alpha $
acts as the transposition
$s_\alpha $
acts as the transposition
![]() $(2, 4)$
. In this case, the set
$(2, 4)$
. In this case, the set
![]() $s_\alpha (R)$
corresponds to the matching
$s_\alpha (R)$
corresponds to the matching
![]() $\{14,25,36\}$
and has type
$\{14,25,36\}$
and has type
![]() $CCC$
. The reflection
$CCC$
. The reflection
![]() $s_\alpha $
changes the alignment
$s_\alpha $
changes the alignment
![]() $Q = \{\varepsilon _1 \pm \varepsilon _2, \ \varepsilon _4 \pm \varepsilon _5\}$
to the crossing
$Q = \{\varepsilon _1 \pm \varepsilon _2, \ \varepsilon _4 \pm \varepsilon _5\}$
to the crossing
![]() $Q'=s_\alpha (Q) = \{\varepsilon _1 \pm \varepsilon _4, \ \varepsilon _2 \pm \varepsilon _5\}$
, so
$Q'=s_\alpha (Q) = \{\varepsilon _1 \pm \varepsilon _4, \ \varepsilon _2 \pm \varepsilon _5\}$
, so
![]() $\alpha $
moves an A to a C. Note that while
$\alpha $
moves an A to a C. Note that while
![]() $s_\alpha $
changes the quadruple Q from an A to a C locally, globally
$s_\alpha $
changes the quadruple Q from an A to a C locally, globally
![]() $s_\alpha $
does not change the type of R from
$s_\alpha $
does not change the type of R from
![]() $AAN$
to
$AAN$
to
![]() $ACN$
but to
$ACN$
but to
![]() $CCC$
. This is because after the application of
$CCC$
. This is because after the application of
![]() $s_\alpha $
, each collinear pair of roots in Q becomes a new collinear pair that forms a new type of coplanar quadruple with the collinear pair of roots
$s_\alpha $
, each collinear pair of roots in Q becomes a new collinear pair that forms a new type of coplanar quadruple with the collinear pair of roots
![]() $\varepsilon _3\pm \varepsilon _6$
outside Q.
$\varepsilon _3\pm \varepsilon _6$
outside Q.
Part (ii) of the next proposition, however, will imply that if
![]() $\alpha $
is minimal among roots moving an A to a C, then the global change in the type of R will mirror this local change, so that if R has type
$\alpha $
is minimal among roots moving an A to a C, then the global change in the type of R will mirror this local change, so that if R has type
![]() $A^pC^qN^r$
, then
$A^pC^qN^r$
, then
![]() $s_\alpha (R)$
has type
$s_\alpha (R)$
has type
![]() $A^{p-1}C^{q+1}N^r$
. In our example, the root
$A^{p-1}C^{q+1}N^r$
. In our example, the root
![]() $\alpha '=\varepsilon _2-\varepsilon _3$
satisfies the minimality condition since it is simple. The reflection
$\alpha '=\varepsilon _2-\varepsilon _3$
satisfies the minimality condition since it is simple. The reflection
![]() $s_{\alpha '}$
changes the coplanar quadruple
$s_{\alpha '}$
changes the coplanar quadruple
![]() $\{\varepsilon _1\pm \varepsilon _2,\varepsilon _3\pm \varepsilon _6\}$
of type A to the coplanar quadruple
$\{\varepsilon _1\pm \varepsilon _2,\varepsilon _3\pm \varepsilon _6\}$
of type A to the coplanar quadruple
![]() $\{\varepsilon _1\pm \varepsilon _3,\varepsilon _2\pm \varepsilon _6\}$
of type C, and changes the set R of type
$\{\varepsilon _1\pm \varepsilon _3,\varepsilon _2\pm \varepsilon _6\}$
of type C, and changes the set R of type
![]() $AAN$
to a maximal orthogonal set of type
$AAN$
to a maximal orthogonal set of type
![]() $ACN$
.
$ACN$
.
Proposition 4.7. Let W be a Weyl group of type
![]() $E_7$
,
$E_7$
,
![]() $E_8$
or
$E_8$
or
![]() $D_{n}$
with n even, and let R be a maximal set of orthogonal positive roots of type
$D_{n}$
with n even, and let R be a maximal set of orthogonal positive roots of type
![]() $A^p C^q N^r$
. Let
$A^p C^q N^r$
. Let
![]() $\lambda =C+2N$
be the level function from Definition 4.2.
$\lambda =C+2N$
be the level function from Definition 4.2.
-
(i) If
 $\alpha _i$
is a simple root, then either
$\alpha _i$
is a simple root, then either
 $\alpha _i \in R$
, or
$\alpha _i \in R$
, or
 $\lambda (s_{\alpha _i}(R)) \ne \lambda (R)$
. If
$\lambda (s_{\alpha _i}(R)) \ne \lambda (R)$
. If
 $\lambda (s_{\alpha _i}(R))> \lambda (R)$
, then we have
$\lambda (s_{\alpha _i}(R))> \lambda (R)$
, then we have
 $\lambda (s_{\alpha _i}(R)) = \lambda (R) + 1$
, and either (1)
$\lambda (s_{\alpha _i}(R)) = \lambda (R) + 1$
, and either (1)
 $s_{\alpha _i}$
moves an A to a C and
$s_{\alpha _i}$
moves an A to a C and
 $s_{\alpha _i}(R)$
has type
$s_{\alpha _i}(R)$
has type
 $A^{p-1}C^{q+1}N^r$
, or (2)
$A^{p-1}C^{q+1}N^r$
, or (2)
 $s_{\alpha _i}$
moves a C to an N and
$s_{\alpha _i}$
moves a C to an N and
 $s_{\alpha _i}(R)$
has type
$s_{\alpha _i}(R)$
has type
 $A^pC^{q-1}N^{r+1}$
.
$A^pC^{q-1}N^{r+1}$
. -
(ii) If Q is an alignment in R,
 $Q'$
is the corresponding crossing quadruple, and
$Q'$
is the corresponding crossing quadruple, and
 $R'=(R\setminus Q)\cup Q'$
, then
$R'=(R\setminus Q)\cup Q'$
, then
 $d = \lambda (R') - \lambda (R)$
is a positive odd number. If there is a positive root
$d = \lambda (R') - \lambda (R)$
is a positive odd number. If there is a positive root
 $\alpha $
such that
$\alpha $
such that
 $s_\alpha (Q)=Q'$
but no positive root
$s_\alpha (Q)=Q'$
but no positive root
 $\alpha '<\alpha $
moves an A in R to a C, then
$\alpha '<\alpha $
moves an A in R to a C, then
 $R'$
has type
$R'$
has type
 $A^{p-1}C^{q+1}N^{r}$
.
$A^{p-1}C^{q+1}N^{r}$
. -
(iii) If Q is a crossing in R,
 $Q'$
is the corresponding nesting quadruple, and
$Q'$
is the corresponding nesting quadruple, and
 $R'=(R\setminus Q)\cup Q'$
, then
$R'=(R\setminus Q)\cup Q'$
, then
 $A(R) = A((R \backslash Q) \cup Q')$
and
$A(R) = A((R \backslash Q) \cup Q')$
and
 $d = \lambda (R') - \lambda (R)$
is a positive odd number. If there is a positive root
$d = \lambda (R') - \lambda (R)$
is a positive odd number. If there is a positive root
 $\alpha $
such that
$\alpha $
such that
 $s_\alpha (Q)=Q'$
but no positive root
$s_\alpha (Q)=Q'$
but no positive root
 $\alpha '<\alpha $
moves a C in R to an N, then
$\alpha '<\alpha $
moves a C in R to an N, then
 $R'$
has type
$R'$
has type
 $A^{p}C^{q-1}N^{r+1}$
.
$A^{p}C^{q-1}N^{r+1}$
. -
(iv) If Q is an alignment in R,
 $Q'$
is the corresponding nesting quadruple, and
$Q'$
is the corresponding nesting quadruple, and
 $R'=(R\setminus Q)\cup Q'$
, then
$R'=(R\setminus Q)\cup Q'$
, then
 $d = \lambda ((R \backslash Q) \cup Q') - \lambda (R)$
is a strictly positive even number.
$d = \lambda ((R \backslash Q) \cup Q') - \lambda (R)$
is a strictly positive even number.
Lemma 4.8. Proposition 4.7 holds if W has type
![]() $D_6$
.
$D_6$
.
Proof of Lemma 4.8.
Throughout the proof, we will identify both R and the coplanar quadruples within R with their corresponding matchings (as in Lemma 3.1 and Remark 3.6). Recall that we will often write a 2-block
![]() $\{a,b\}$
in a matching as
$\{a,b\}$
in a matching as
![]() $ab$
.
$ab$
.
Suppose that
![]() $\alpha _i$
is a simple root, so that the reflection
$\alpha _i$
is a simple root, so that the reflection
![]() $s_{\alpha _i}$
acts as the transposition
$s_{\alpha _i}$
acts as the transposition
![]() $(i, i+1)$
. We will assume that
$(i, i+1)$
. We will assume that
![]() $\alpha _i \not \in R$
, so that we have
$\alpha _i \not \in R$
, so that we have
![]() $R=\{ai,(i+1)b,ef\}$
and the coplanar quadruple moved by
$R=\{ai,(i+1)b,ef\}$
and the coplanar quadruple moved by
![]() $s_{\alpha _i}$
is
$s_{\alpha _i}$
is
![]() $Q=\{ai,(i+1)b\}$
. Let
$Q=\{ai,(i+1)b\}$
. Let
![]() $Q'$
be any other coplanar quadruple in R. Then
$Q'$
be any other coplanar quadruple in R. Then
![]() $Q'$
is of the form
$Q'$
is of the form
![]() $\{xy,ef\}$
with
$\{xy,ef\}$
with
![]() $x\in \{a,b\}$
and
$x\in \{a,b\}$
and
![]() $y\in \{i,i+1\}$
, and we have
$y\in \{i,i+1\}$
, and we have
![]() $s_{\alpha _i}(Q')=\{\{x,s_{\alpha _i}(y)\},ef\}$
. Since the numbers i and
$s_{\alpha _i}(Q')=\{\{x,s_{\alpha _i}(y)\},ef\}$
. Since the numbers i and
![]() $i+1$
are only distance 1 apart, the four elements
$i+1$
are only distance 1 apart, the four elements
![]() $x, s_{\alpha _i}(y), e,f$
appearing in
$x, s_{\alpha _i}(y), e,f$
appearing in
![]() $Q'$
have the same relative order as the numbers
$Q'$
have the same relative order as the numbers
![]() $x,y,e,f$
; therefore,
$x,y,e,f$
; therefore,
![]() $Q'$
and
$Q'$
and
![]() $s_{\alpha _i}(Q')$
have the same type. It follows that Q is the only quadruple in R that is changed to a quadruple of another type by
$s_{\alpha _i}(Q')$
have the same type. It follows that Q is the only quadruple in R that is changed to a quadruple of another type by
![]() $s_{\alpha _i}$
. Note that Q will be an alignment if
$s_{\alpha _i}$
. Note that Q will be an alignment if
![]() $a < i < i+1 < b$
; Q will be a crossing if
$a < i < i+1 < b$
; Q will be a crossing if
![]() $a < b < i$
or
$a < b < i$
or
![]() $i+1 < a < b$
or
$i+1 < a < b$
or
![]() $b < i < i+1 < a$
; and Q will be a nesting if
$b < i < i+1 < a$
; and Q will be a nesting if
![]() $b < a < i$
or
$b < a < i$
or
![]() $i+1 < b < a$
. We have
$i+1 < b < a$
. We have
![]() $\lambda (s_{\alpha _i}(R)) = \lambda (R)+1$
in the first three of these six cases and
$\lambda (s_{\alpha _i}(R)) = \lambda (R)+1$
in the first three of these six cases and
![]() $\lambda (s_{\alpha _i}(R))=\lambda (R)-1$
in the last three cases. The first of the six cases corresponds to the situation in (1), and the second and third cases correspond to the situation in (2). Part (i) follows.
$\lambda (s_{\alpha _i}(R))=\lambda (R)-1$
in the last three cases. The first of the six cases corresponds to the situation in (1), and the second and third cases correspond to the situation in (2). Part (i) follows.
Suppose that Q and
![]() $Q'$
are as in the statement of (ii), with Q being the alignment
$Q'$
are as in the statement of (ii), with Q being the alignment
![]() $\{a_1a_2,b_1b_2\}$
for some
$\{a_1a_2,b_1b_2\}$
for some
![]() $a_1 < a_2 < b_1 < b_2$
. If
$a_1 < a_2 < b_1 < b_2$
. If
![]() $b_1 = a_2 + 1$
, then the simple root
$b_1 = a_2 + 1$
, then the simple root
![]() $s_{a_2}$
moves an A to a C by moving Q, and we have
$s_{a_2}$
moves an A to a C by moving Q, and we have
![]() $R'=s_{\alpha _2}(R)$
; therefore,
$R'=s_{\alpha _2}(R)$
; therefore,
![]() $R'$
has type
$R'$
has type
![]() $A^{p-1}C^{q+1}N^{r}$
by (i). If
$A^{p-1}C^{q+1}N^{r}$
by (i). If
![]() $b_1>a_2+1$
, then Q must be one of the following five quadruples:
$b_1>a_2+1$
, then Q must be one of the following five quadruples:
Direct computation shows that d equals
![]() $5,1,3,1$
and
$5,1,3,1$
and
![]() $3$
in these cases, respectively. It follows that d is a positive odd number.
$3$
in these cases, respectively. It follows that d is a positive odd number.
To prove the second assertion in (ii), we prove its contrapositive. If
![]() $R'$
does not have type
$R'$
does not have type
![]() $A^{p-1}C^{q+1}N^r$
, then Q must be one of five quadruples listed in the last paragraph. We claim that in each case, for every positive root
$A^{p-1}C^{q+1}N^r$
, then Q must be one of five quadruples listed in the last paragraph. We claim that in each case, for every positive root
![]() $\alpha $
such that
$\alpha $
such that
![]() $s_\alpha (Q)=Q'$
, there exists a positive root
$s_\alpha (Q)=Q'$
, there exists a positive root
![]() $\alpha '<\alpha $
that moves another alignment in R other than Q to a crossing. Specifically, we may always take
$\alpha '<\alpha $
that moves another alignment in R other than Q to a crossing. Specifically, we may always take
![]() $\alpha '$
to be
$\alpha '$
to be
![]() $\varepsilon _2-\varepsilon _3$
in the first three cases and
$\varepsilon _2-\varepsilon _3$
in the first three cases and
![]() $\varepsilon _4-\varepsilon _5$
in the last two cases. For example, the only possibilities for
$\varepsilon _4-\varepsilon _5$
in the last two cases. For example, the only possibilities for
![]() $\alpha $
if
$\alpha $
if
![]() $Q=\{12,56\}$
are
$Q=\{12,56\}$
are
![]() $\varepsilon _2\pm \varepsilon _5$
and
$\varepsilon _2\pm \varepsilon _5$
and
![]() $\varepsilon _1\pm \varepsilon _6$
, and for all these possibilities the root
$\varepsilon _1\pm \varepsilon _6$
, and for all these possibilities the root
![]() $\alpha '=\varepsilon _2-\varepsilon _3$
is smaller than
$\alpha '=\varepsilon _2-\varepsilon _3$
is smaller than
![]() $\alpha $
and moves an alignment in R other than Q to a crossing. This completes the proof of the desired contrapositive.
$\alpha $
and moves an alignment in R other than Q to a crossing. This completes the proof of the desired contrapositive.
A similar argument proves (iii). This time, we have
![]() $Q= \{a_1a_2,b_1b_2\}$
for some
$Q= \{a_1a_2,b_1b_2\}$
for some
![]() $a_1 < b_1 < a_2 < b_2$
. If we have
$a_1 < b_1 < a_2 < b_2$
. If we have
![]() $b_1=a_1+1$
or
$b_1=a_1+1$
or
![]() $b_2=a_2+1$
, then the simple root
$b_2=a_2+1$
, then the simple root
![]() $\alpha _{a_1}$
or
$\alpha _{a_1}$
or
![]() $\alpha _{a_2}$
moves Q to a nesting
$\alpha _{a_2}$
moves Q to a nesting
![]() $Q'$
, so
$Q'$
, so
![]() $R'$
has type
$R'$
has type
![]() $A^pC^{q-1}N^{r+1}$
by (i). The only remaining possibility for Q is
$A^pC^{q-1}N^{r+1}$
by (i). The only remaining possibility for Q is
![]() $\{14,36\}$
. If
$\{14,36\}$
. If
![]() $\alpha $
is a positive root such that
$\alpha $
is a positive root such that
![]() $s_\alpha (Q)=Q'$
, then
$s_\alpha (Q)=Q'$
, then
![]() $\alpha \in \{\varepsilon _1\pm \varepsilon _3,\varepsilon _4\pm \varepsilon _6\}$
. Direct computation shows that any simple root
$\alpha \in \{\varepsilon _1\pm \varepsilon _3,\varepsilon _4\pm \varepsilon _6\}$
. Direct computation shows that any simple root
![]() $\alpha '<\alpha $
moves some crossing in R other than Q to a nesting.
$\alpha '<\alpha $
moves some crossing in R other than Q to a nesting.
Finally, (iv) follows by combining (ii) and (iii) since
![]() $R'$
can be obtained from by first replacing Q in R with its corresponding crossing
$R'$
can be obtained from by first replacing Q in R with its corresponding crossing
![]() $Q"$
and then replacing
$Q"$
and then replacing
![]() $Q"$
in the result with
$Q"$
in the result with
![]() $Q'$
.
$Q'$
.
Proof of Proposition 4.7.
If W has type
![]() $D_4$
then there are only three possibilities for R, and all the assertions follow by direct verification. By Lemma 4.8, we may therefore assume that the rank of W is at least
$D_4$
then there are only three possibilities for R, and all the assertions follow by direct verification. By Lemma 4.8, we may therefore assume that the rank of W is at least
![]() $7$
.
$7$
.
For each coplanar quadruple
![]() $Q\subseteq R$
, we define
$Q\subseteq R$
, we define
![]() $H_Q$
to be the set of all 6-subsets H of R such that there exists a
$H_Q$
to be the set of all 6-subsets H of R such that there exists a
![]() $D_6$
-subsystem of
$D_6$
-subsystem of
![]() $\Phi $
containing both
$\Phi $
containing both
![]() $\Psi _Q$
and H, where
$\Psi _Q$
and H, where
![]() $\Psi _Q$
is the
$\Psi _Q$
is the
![]() $D_4$
-subsystem associated with Q. By Proposition 3.20, if
$D_4$
-subsystem associated with Q. By Proposition 3.20, if
![]() $Q_1$
is any coplanar quadruple in R, then either
$Q_1$
is any coplanar quadruple in R, then either
![]() $Q_1=Q$
, or
$Q_1=Q$
, or
![]() $Q_1 \cap Q = \emptyset $
, or
$Q_1 \cap Q = \emptyset $
, or
![]() $\lvert Q_1\cap Q \rvert =2$
and there is a unique element of
$\lvert Q_1\cap Q \rvert =2$
and there is a unique element of
![]() $H_\Psi $
that contains both Q and
$H_\Psi $
that contains both Q and
![]() $Q_1$
.
$Q_1$
.
We now prove (iii). By tracking the contributions towards the crossing number made by the three types of coplanar quadruples
![]() $Q_1\subseteq R$
just mentioned, we note that
$Q_1\subseteq R$
just mentioned, we note that
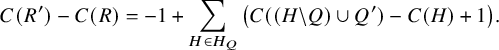 $$ \begin{align} C(R') - C(R) = -1 + \sum_{H \in H_Q} \big(C((H \backslash Q) \cup Q') - C(H) + 1 \big). \end{align} $$
$$ \begin{align} C(R') - C(R) = -1 + \sum_{H \in H_Q} \big(C((H \backslash Q) \cup Q') - C(H) + 1 \big). \end{align} $$
Here, the term
![]() $-1$
comes from the case
$-1$
comes from the case
![]() $Q_1=Q$
since the crossing Q in R is replaced by the non-crossing feature
$Q_1=Q$
since the crossing Q in R is replaced by the non-crossing feature
![]() $Q'$
as we change R to
$Q'$
as we change R to
![]() $R'$
. In the second case where
$R'$
. In the second case where
![]() $Q_1\cap Q=\emptyset $
, the quadruple
$Q_1\cap Q=\emptyset $
, the quadruple
![]() $Q_1$
lies in both R and
$Q_1$
lies in both R and
![]() $R'$
and thus does not contribute to the difference
$R'$
and thus does not contribute to the difference
![]() $C(R')-C(R)$
. Finally, every
$C(R')-C(R)$
. Finally, every
![]() $Q_1$
with
$Q_1$
with
![]() $\lvert Q_1\cap Q \rvert =2$
appears together with Q in a unique element H of
$\lvert Q_1\cap Q \rvert =2$
appears together with Q in a unique element H of
![]() $H_Q$
and contributes a term in the sum over
$H_Q$
and contributes a term in the sum over
![]() $H_Q$
, where we have added 1 to the difference
$H_Q$
, where we have added 1 to the difference
![]() $C((H\backslash Q)\cup Q')-C(H)$
to account for the fact that the change from Q to
$C((H\backslash Q)\cup Q')-C(H)$
to account for the fact that the change from Q to
![]() $Q'$
in H has been recorded by the term
$Q'$
in H has been recorded by the term
![]() $-1$
in the first case.
$-1$
in the first case.
Similar arguments based on the facts that
![]() $N(Q')=N(Q)+1$
and
$N(Q')=N(Q)+1$
and
![]() $A(Q')=A(Q)$
show that
$A(Q')=A(Q)$
show that
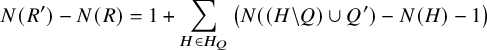 $$ \begin{align} N(R') - N(R) = 1 + \sum_{H \in H_Q} \big(N((H \backslash Q) \cup Q') - N(H) - 1 \big) \end{align} $$
$$ \begin{align} N(R') - N(R) = 1 + \sum_{H \in H_Q} \big(N((H \backslash Q) \cup Q') - N(H) - 1 \big) \end{align} $$
and
 $$ \begin{align} A(R') - A(R) = \sum_{H \in H_Q} \big(A((H \backslash Q) \cup Q') - A(H) \big). \end{align} $$
$$ \begin{align} A(R') - A(R) = \sum_{H \in H_Q} \big(A((H \backslash Q) \cup Q') - A(H) \big). \end{align} $$
Since
![]() $\lambda =C+2N$
, it follows from Equations (4.1) and (4.2) that
$\lambda =C+2N$
, it follows from Equations (4.1) and (4.2) that
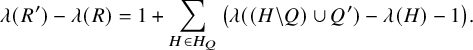 $$ \begin{align} \lambda(R') - \lambda(R) = 1 + \sum_{H \in H_Q} \big(\lambda((H \backslash Q) \cup Q') - \lambda(H) - 1 \big). \end{align} $$
$$ \begin{align} \lambda(R') - \lambda(R) = 1 + \sum_{H \in H_Q} \big(\lambda((H \backslash Q) \cup Q') - \lambda(H) - 1 \big). \end{align} $$
By Lemma 4.8.(iii), each summand in the sum over
![]() $H_Q$
is zero in Equation (4.3) and is a nonnegative even number in Equation (4.4); therefore, we have
$H_Q$
is zero in Equation (4.3) and is a nonnegative even number in Equation (4.4); therefore, we have
![]() $A(R')=A(R)$
, and the number
$A(R')=A(R)$
, and the number
![]() $d=\lambda (R')-\lambda (R)$
is a positive odd number.
$d=\lambda (R')-\lambda (R)$
is a positive odd number.
To prove the last assertion in (ii), suppose that
![]() $s_\alpha (Q)=Q'$
for some positive root
$s_\alpha (Q)=Q'$
for some positive root
![]() $\alpha $
, but no positive root
$\alpha $
, but no positive root
![]() $\alpha ' < \alpha $
moves a C to an N in R. The same minimality condition then applies if R is replaced by an element of
$\alpha ' < \alpha $
moves a C to an N in R. The same minimality condition then applies if R is replaced by an element of
![]() $H_Q$
, so every summand in the sums over
$H_Q$
, so every summand in the sums over
![]() $H_Q$
in Equations (4.1) and (4.2) is zero by Lemma 4.8 (iii). It follows that
$H_Q$
in Equations (4.1) and (4.2) is zero by Lemma 4.8 (iii). It follows that
![]() $R'$
has type
$R'$
has type
![]() $A^pC^{q-1}N^{r+1}$
, which proves Proposition 4.7 (iii).
$A^pC^{q-1}N^{r+1}$
, which proves Proposition 4.7 (iii).
The proof of Proposition 4.7 (ii) follows by a similar but shorter argument, and the proof of Proposition 4.7 (iv) follows by combining parts (ii) and (iii).
Finally, to prove Proposition 4.7 (i), assume that
![]() $\alpha _i$
is a simple root such that
$\alpha _i$
is a simple root such that
![]() $\alpha _i \not \in R$
. We have already proved part (i) if W has type
$\alpha _i \not \in R$
. We have already proved part (i) if W has type
![]() $D_4$
, and this implies that either
$D_4$
, and this implies that either
![]() $\alpha _i$
moves an A to a C or a C to an N. In the former case, the conclusions follow from part (ii), and in the latter case, they follow from part (iii), in each case because the simple root
$\alpha _i$
moves an A to a C or a C to an N. In the former case, the conclusions follow from part (ii), and in the latter case, they follow from part (iii), in each case because the simple root
![]() $\alpha _i$
is minimal in the order
$\alpha _i$
is minimal in the order
![]() $\le $
.
$\le $
.
Proof of Theorem 4.5.
We first prove (i). Proposition 4.7 (i) proves that
![]() $(X, \lambda )$
is a scaled W-set, so it suffices to show
$(X, \lambda )$
is a scaled W-set, so it suffices to show
![]() $(X,\lambda )$
satisfies the axioms (QP1) and (QP2). We do so by induction on n.
$(X,\lambda )$
satisfies the axioms (QP1) and (QP2). We do so by induction on n.
If
![]() $n=4$
or
$n=4$
or
![]() $n=6$
, then W has type D, and the axioms (QP1) and (QP2) can be proved by direct verification or as follows. Suppose
$n=6$
, then W has type D, and the axioms (QP1) and (QP2) can be proved by direct verification or as follows. Suppose
![]() $n=2k$
. By Remark 3.7, it suffices to show that
$n=2k$
. By Remark 3.7, it suffices to show that
![]() $(X,\lambda )$
is a quasiparabolic set for the symmetric group
$(X,\lambda )$
is a quasiparabolic set for the symmetric group
![]() $S_{n}$
. We may identify the set X with the set
$S_{n}$
. We may identify the set X with the set
![]() $X'$
of fixed-point free involutions in
$X'$
of fixed-point free involutions in
![]() $S_{n}=W(A_{n-1})$
, with each collinear pair
$S_{n}=W(A_{n-1})$
, with each collinear pair
![]() $\{\varepsilon _i\pm \varepsilon _j\}$
in a maximal set
$\{\varepsilon _i\pm \varepsilon _j\}$
in a maximal set
![]() $R\in X$
corresponding to a factor
$R\in X$
corresponding to a factor
![]() $(i,j)$
in an involution
$(i,j)$
in an involution
![]() $\iota \in X'$
. Under this identification, the actions of
$\iota \in X'$
. Under this identification, the actions of
![]() $S_n$
on
$S_n$
on
![]() $X'$
and X coincide with each other, so it suffices to show that
$X'$
and X coincide with each other, so it suffices to show that
![]() $X'$
is a quasiparabolic set for
$X'$
is a quasiparabolic set for
![]() $S_n$
under the level function
$S_n$
under the level function
![]() $\lambda $
. Rains and Vazirani [Reference Rains and Vazirani43, Section 4] proved that
$\lambda $
. Rains and Vazirani [Reference Rains and Vazirani43, Section 4] proved that
![]() $X'$
is a quasiparabolic set for
$X'$
is a quasiparabolic set for
![]() $S_n$
under the level function h given by
$S_n$
under the level function h given by
![]() $h(\iota )=(\ell (\iota ) - k)/2$
, where
$h(\iota )=(\ell (\iota ) - k)/2$
, where
![]() $\ell $
denotes Coxeter length, so it further suffices to show that whenever an involution
$\ell $
denotes Coxeter length, so it further suffices to show that whenever an involution
![]() $\iota \in S_n$
corresponds to a maximal set R of positive orthogonal roots, we have
$\iota \in S_n$
corresponds to a maximal set R of positive orthogonal roots, we have
![]() $(\ell (\iota ) - k)/2 = \lambda (R)$
. This can be proved by an exhaustive check or by induction on
$(\ell (\iota ) - k)/2 = \lambda (R)$
. This can be proved by an exhaustive check or by induction on
![]() $\lambda (R)$
by using the first three cases in the second paragraph of the proof of Lemma 4.8. For example, the involution
$\lambda (R)$
by using the first three cases in the second paragraph of the proof of Lemma 4.8. For example, the involution
corresponds to the set
![]() $R=\{13,26,45\}$
of type
$R=\{13,26,45\}$
of type
![]() $ACN$
. In this case, we have
$ACN$
. In this case, we have
![]() $(\ell (\iota ) - k)/2 = (9-3)/2$
and
$(\ell (\iota ) - k)/2 = (9-3)/2$
and
![]() $\lambda (R)=3$
, as required.
$\lambda (R)=3$
, as required.
Now assume
![]() $n\ge 7$
. Let
$n\ge 7$
. Let
![]() $r=s_\alpha \in T$
be the reflection corresponding to a root
$r=s_\alpha \in T$
be the reflection corresponding to a root
![]() $\alpha $
, and let
$\alpha $
, and let
![]() $x \in X$
. If
$x \in X$
. If
![]() $rx \ne x$
, then
$rx \ne x$
, then
![]() $\pm \alpha $
are not in x, so r moves an A to a C, or a C to an N, or an A to an N, or vice versa by Remark 3.12. It follows from Proposition 4.7 (ii), (iii) and (iv) that
$\pm \alpha $
are not in x, so r moves an A to a C, or a C to an N, or an A to an N, or vice versa by Remark 3.12. It follows from Proposition 4.7 (ii), (iii) and (iv) that
![]() $\lambda (rx)> \lambda (x)$
in all the first three cases and
$\lambda (rx)> \lambda (x)$
in all the first three cases and
![]() $\lambda (rx)<\lambda (x)$
in the last three cases; therefore, axiom (QP1) holds.
$\lambda (rx)<\lambda (x)$
in the last three cases; therefore, axiom (QP1) holds.
To prove axiom (QP2), assume that we have
![]() $r \in T$
,
$r \in T$
,
![]() $x \in X$
,
$x \in X$
,
![]() $s \in S$
,
$s \in S$
,
![]() $\lambda (rx)> \lambda (x)$
and
$\lambda (rx)> \lambda (x)$
and
![]() $\lambda (srx) < \lambda (sx)$
. Then the definition of scaled W-sets forces
$\lambda (srx) < \lambda (sx)$
. Then the definition of scaled W-sets forces
![]() $\lambda (rx) =\lambda (sx)= \lambda (x)+1$
, so each of r and s must be an
$\lambda (rx) =\lambda (sx)= \lambda (x)+1$
, so each of r and s must be an
![]() $AC$
or
$AC$
or
![]() $CN$
move by Proposition 4.7 (ii), (iii) and (iv). Let
$CN$
move by Proposition 4.7 (ii), (iii) and (iv). Let
![]() $Q_1$
and
$Q_1$
and
![]() $Q_2$
be the coplanar quadruples of roots in R moved by r and s, respectively. Then
$Q_2$
be the coplanar quadruples of roots in R moved by r and s, respectively. Then
![]() $Q_1$
and
$Q_1$
and
![]() $Q_2$
are disjoint, or coincide with each other, or intersect in two elements by Proposition 3.20. If
$Q_2$
are disjoint, or coincide with each other, or intersect in two elements by Proposition 3.20. If
![]() $Q_1$
and
$Q_1$
and
![]() $Q_2$
were disjoint, we would have
$Q_2$
were disjoint, we would have
![]() $Q_2\subseteq r(R)$
, so that s would move
$Q_2\subseteq r(R)$
, so that s would move
![]() $Q_2$
in
$Q_2$
in
![]() $r(R)$
, and Proposition 4.7 (ii) and (iii) would imply that
$r(R)$
, and Proposition 4.7 (ii) and (iii) would imply that
![]() $ \lambda (srx)=\lambda (rx)+1>\lambda (rx)=\lambda (sx), $
contradicting the assumption that
$ \lambda (srx)=\lambda (rx)+1>\lambda (rx)=\lambda (sx), $
contradicting the assumption that
![]() $\lambda (srx)<\lambda (sx)$
. If
$\lambda (srx)<\lambda (sx)$
. If
![]() $Q_1=Q_2$
, then the fact that
$Q_1=Q_2$
, then the fact that
![]() $\lambda (rx)=\lambda (sx)=\lambda (x)+1$
implies that s and r must both be
$\lambda (rx)=\lambda (sx)=\lambda (x)+1$
implies that s and r must both be
![]() $AC$
moves or both be
$AC$
moves or both be
![]() $CN$
moves, according as
$CN$
moves, according as
![]() $Q_1=Q_2$
is an alignment or crossing, by Proposition 4.7. It follows from Remark 3.12 that
$Q_1=Q_2$
is an alignment or crossing, by Proposition 4.7. It follows from Remark 3.12 that
![]() $rx=sx$
. Finally, if
$rx=sx$
. Finally, if
![]() $\lvert Q_1\cap Q_2 \rvert =2$
, then Proposition 3.20 implies that there is a subsystem
$\lvert Q_1\cap Q_2 \rvert =2$
, then Proposition 3.20 implies that there is a subsystem
![]() $\Sigma $
of type
$\Sigma $
of type
![]() $D_6$
containing both
$D_6$
containing both
![]() $Q_1$
and
$Q_1$
and
![]() $Q_2$
. Applying the inductive hypothesis to
$Q_2$
. Applying the inductive hypothesis to
![]() $\Sigma $
proves that
$\Sigma $
proves that
![]() $rx = sx$
, which completes the proof.
$rx = sx$
, which completes the proof.
We end this subsection by recording some useful consequences of Proposition 4.7 concerning sums of n-roots:
Corollary 4.9. Let W be a Weyl group of type
![]() $E_7$
,
$E_7$
,
![]() $E_8$
or
$E_8$
or
![]() $D_{n}$
with n even.
$D_{n}$
with n even.
-
(i) If
 $\beta \leq _Q \gamma $
are two positive n-roots that are comparable in the quasiparabolic order, then we have
$\beta \leq _Q \gamma $
are two positive n-roots that are comparable in the quasiparabolic order, then we have
 $\sigma (\beta ) \leq \sigma (\gamma )$
, with equality if and only if we have
$\sigma (\beta ) \leq \sigma (\gamma )$
, with equality if and only if we have
 $A(\beta ) = A(\gamma )$
.
$A(\beta ) = A(\gamma )$
. -
(ii) If
 $\alpha _i$
is a simple root and R is a maximal orthogonal set of positive roots, then we have
$\alpha _i$
is a simple root and R is a maximal orthogonal set of positive roots, then we have 
-
(iii) If
 $\alpha _i$
is a simple root and
$\alpha _i$
is a simple root and
 $\beta $
is a positive n-root of type
$\beta $
is a positive n-root of type
 $A^pC^qN^r$
such that
$A^pC^qN^r$
such that
 $\sigma (s_{\alpha _i}(\beta ))> \sigma (\beta )$
, then
$\sigma (s_{\alpha _i}(\beta ))> \sigma (\beta )$
, then
 $s_{\alpha _i}(\beta )$
is a positive n-root of type
$s_{\alpha _i}(\beta )$
is a positive n-root of type
 $A^{p-1}C^{q+1}N^r$
, and we have
$A^{p-1}C^{q+1}N^r$
, and we have
 $\sigma (s_{\alpha _i}(\beta )) - \sigma (\beta ) = 2\alpha _i$
. If
$\sigma (s_{\alpha _i}(\beta )) - \sigma (\beta ) = 2\alpha _i$
. If
 $\beta $
is nonnesting, then so is
$\beta $
is nonnesting, then so is
 $s_{\alpha _i}(\beta )$
.
$s_{\alpha _i}(\beta )$
.
Proof. All the claims can be proved by examining the effects of various types of (simple) reflections on sums and levels of n-roots recorded in Theorem 3.10 and Proposition 4.7. We first prove (i). By the definition of
![]() $\le _Q$
, it is enough to consider the case where
$\le _Q$
, it is enough to consider the case where
![]() $r \in T$
is a reflection and
$r \in T$
is a reflection and
![]() $\gamma = r(\beta )$
satisfies
$\gamma = r(\beta )$
satisfies
![]() $\lambda (\beta )<\lambda (\gamma )$
. By Proposition 4.7, this implies that r is an
$\lambda (\beta )<\lambda (\gamma )$
. By Proposition 4.7, this implies that r is an
![]() $AC$
,
$AC$
,
![]() $CN$
or
$CN$
or
![]() $AN$
move. The proof of (i) then follows from Theorem 3.10 (vi).
$AN$
move. The proof of (i) then follows from Theorem 3.10 (vi).
We now prove (ii). If
![]() $\alpha _i \in R$
, then
$\alpha _i \in R$
, then
![]() $\sigma (s_i(R))=\sigma (R)-2\alpha _i$
because
$\sigma (s_i(R))=\sigma (R)-2\alpha _i$
because
![]() $s_{i}(\alpha _i) = -\alpha _i$
. If
$s_{i}(\alpha _i) = -\alpha _i$
. If
![]() $\alpha _i$
is a
$\alpha _i$
is a
![]() $CN$
or
$CN$
or
![]() $NC$
move, Theorem 3.10 (vi) implies that
$NC$
move, Theorem 3.10 (vi) implies that
![]() $\sigma (s_{\alpha _i}(R)) = \sigma (R)$
. It follows from Proposition 4.7 (i) that the only other possibility is that
$\sigma (s_{\alpha _i}(R)) = \sigma (R)$
. It follows from Proposition 4.7 (i) that the only other possibility is that
![]() $\alpha _i$
moves an A to a C or vice versa. By Theorem 3.10 (vi), this can only happen if
$\alpha _i$
moves an A to a C or vice versa. By Theorem 3.10 (vi), this can only happen if
![]() $\alpha _i$
is the unique simple root in the corresponding nesting (i.e., the root
$\alpha _i$
is the unique simple root in the corresponding nesting (i.e., the root
![]() $\alpha _2$
in the explicitly constructed sets
$\alpha _2$
in the explicitly constructed sets
![]() $\Psi _2^+=\Psi ^+_N$
in the proof of that theorem). Explicit computation shows that root sums in this case differ by
$\Psi _2^+=\Psi ^+_N$
in the proof of that theorem). Explicit computation shows that root sums in this case differ by
![]() $2\alpha _i$
in the precise manner described in the statement, which completes the proof of (ii).
$2\alpha _i$
in the precise manner described in the statement, which completes the proof of (ii).
The first part of (iii) follows immediately from (ii) and Proposition 4.7 (i). The assertion about nonnesting n-roots follows from the special case
![]() $r=0$
.
$r=0$
.
Remark 4.10. Burns and Pfeiffer [Reference Burns and Pfeiffer9, Theorem 1.2] prove that if T is a maximal order abelian subgroup of one of the groups W in Theorem 4.5, then T is elementary abelian of order
![]() $2^n$
, where n is the rank of W. They also prove that the set of all such subgroups forms a single conjugacy class [Reference Burns and Pfeiffer9, Theorem 3.1]. It follows that the stabilizers of the elements
$2^n$
, where n is the rank of W. They also prove that the set of all such subgroups forms a single conjugacy class [Reference Burns and Pfeiffer9, Theorem 3.1]. It follows that the stabilizers of the elements
![]() $x \in X$
can be defined abstractly from the group structure of W: they are the normalizers of the maximal order abelian subgroups of W.
$x \in X$
can be defined abstractly from the group structure of W: they are the normalizers of the maximal order abelian subgroups of W.
4.3 Extremal elements
In this subsection, we identify X with the set
![]() $\Phi ^+_n$
of positive n-roots as usual and discuss an application of Theorem 4.5 concerning the maximally aligned and maximally nested n-roots, which turn out to be the unique W-minimal and W-maximal elements of the set X. The uniqueness of the maximally aligned and maximally nested n-root is not a priori clear, but it will follow conveniently from the general theory of quasiparabolic sets.
$\Phi ^+_n$
of positive n-roots as usual and discuss an application of Theorem 4.5 concerning the maximally aligned and maximally nested n-roots, which turn out to be the unique W-minimal and W-maximal elements of the set X. The uniqueness of the maximally aligned and maximally nested n-root is not a priori clear, but it will follow conveniently from the general theory of quasiparabolic sets.
Proposition 4.11. Let W be a Weyl group of rank n of types
![]() $E_7$
,
$E_7$
,
![]() $E_8$
or
$E_8$
or
![]() $D_n$
for n even, and let M be the number of coplanar quadruples in a positive n-root.
$D_n$
for n even, and let M be the number of coplanar quadruples in a positive n-root.
-
(i) There is a unique positive n-root,
 $\theta _A$
, of type
$\theta _A$
, of type
 $A^M$
, and it corresponds to the unique W-minimal element of the quasiparabolic set X of Theorem 4.5.
$A^M$
, and it corresponds to the unique W-minimal element of the quasiparabolic set X of Theorem 4.5. -
(ii) There is a unique positive n-root,
 $\theta _N$
, of type
$\theta _N$
, of type
 $N^M$
, and it corresponds to the unique W-maximal element of the quasiparabolic set X of Theorem 4.5.
$N^M$
, and it corresponds to the unique W-maximal element of the quasiparabolic set X of Theorem 4.5.
Proof. We recall that by Theorem 2.8, Remark 2.9 and Corollary 2.10 of [Reference Rains and Vazirani43], every orbit of a quasiparabolic set contains at most one W-minimal and at most one W-maximal element. If such a W-minimal or W-maximal element exists, then it can be identified as the unique element in the orbit with the minimal or maximal possible level, respectively.
The set X is finite, so it has at least one W-maximal and one W-minimal element. Since X consists of a single W-orbit by Lemma 3.2, it follows from the paragraph preceding this proposition that X has a unique W-maximal and a unique W-minimal element, and that they are the unique elements with the minimal and maximal possible level.
Let R be a maximal orthogonal set of positive roots. If R contains any coplanar quadruple Q that is a crossing or a nesting, then by Remark 3.12, we can find a reflection
![]() $s_\alpha $
that moves Q to an alignment or a crossing, respectively, and in both cases, Proposition 4.7 implies that
$s_\alpha $
that moves Q to an alignment or a crossing, respectively, and in both cases, Proposition 4.7 implies that
![]() $\lambda (s_\alpha (R))<\lambda (R)$
. Iterating this procedure proves the existence of an n-root of type
$\lambda (s_\alpha (R))<\lambda (R)$
. Iterating this procedure proves the existence of an n-root of type
![]() $A^M$
, which achieves the lowest possible value of
$A^M$
, which achieves the lowest possible value of
![]() $\lambda $
. The uniqueness property of the previous paragraph then completes the proof of (i). Part (ii) can be proved similarly, by using the fact that any alignment or crossing in R would induce a level-increasing
$\lambda $
. The uniqueness property of the previous paragraph then completes the proof of (i). Part (ii) can be proved similarly, by using the fact that any alignment or crossing in R would induce a level-increasing
![]() $AC$
or
$AC$
or
![]() $CN$
move.
$CN$
move.
We will prove shortly, in Proposition 5.2, that W also has a unique maximally crossing element,
![]() $\theta _C$
. The element
$\theta _C$
. The element
![]() $\theta _C$
will be the unique minimal element in a quasiparabolic set of a parabolic subgroup of W.
$\theta _C$
will be the unique minimal element in a quasiparabolic set of a parabolic subgroup of W.
Remark 4.12. In Theorem 5.7 below, we will introduce another partial order,
![]() $\leq _{\mathcal B}$
, on the positive n-roots. The argument of [Reference Green and Xu30, Section 6] can be adapted to show that, under suitable identifications,
$\leq _{\mathcal B}$
, on the positive n-roots. The argument of [Reference Green and Xu30, Section 6] can be adapted to show that, under suitable identifications,
![]() $\leq _{\mathcal B}$
refines the monoidal order introduced by Cohen, Gijsbers and Wales [Reference Cohen, Gijsbers and Wales17, Section 3]. The quasiparabolic order has
$\leq _{\mathcal B}$
refines the monoidal order introduced by Cohen, Gijsbers and Wales [Reference Cohen, Gijsbers and Wales17, Section 3]. The quasiparabolic order has
![]() $\theta _N$
and
$\theta _N$
and
![]() $\theta _A$
as its unique maximal and unique minimal elements, whereas the monoidal order (and
$\theta _A$
as its unique maximal and unique minimal elements, whereas the monoidal order (and
![]() $\leq _{\mathcal B}$
) has
$\leq _{\mathcal B}$
) has
![]() $\theta _C$
as its unique maximal element and has multiple minimal elements.
$\theta _C$
as its unique maximal element and has multiple minimal elements.
5 Feature-avoiding elements
In this section, we develop the properties of n-roots that avoid features of a given type: the alignment-free, noncrossing and nonnesting elements. We show that the alignment-free elements form a quasiparabolic set
![]() $X_I$
of a maximal standard parabolic subgroup
$X_I$
of a maximal standard parabolic subgroup
![]() $W_I$
of W, and that the unique maximally crossing n-root
$W_I$
of W, and that the unique maximally crossing n-root
![]() $\theta _C$
is the unique
$\theta _C$
is the unique
![]() $W_I$
-minimal element of
$W_I$
-minimal element of
![]() $X_I$
. We also show that the sets of noncrossing elements and of nonnesting elements both form bases of the Macdonald representation
$X_I$
. We also show that the sets of noncrossing elements and of nonnesting elements both form bases of the Macdonald representation
![]() $j^{\Phi }_{nA_1}({\mathrm {sgn}})$
(Definition 1.1). Moreover, the basis of noncrossing elements may be viewed as a canonical basis and behaves in a way that is reminiscent of the set of simple roots of a root system (Theorem 5.7). The basis of nonnesting elements admits an interesting combinatorial characterization: it is a distributive lattice induced by a suitable Bruhat order (Theorem 5.13). Finally, we introduce the notion of
$j^{\Phi }_{nA_1}({\mathrm {sgn}})$
(Definition 1.1). Moreover, the basis of noncrossing elements may be viewed as a canonical basis and behaves in a way that is reminiscent of the set of simple roots of a root system (Theorem 5.7). The basis of nonnesting elements admits an interesting combinatorial characterization: it is a distributive lattice induced by a suitable Bruhat order (Theorem 5.13). Finally, we introduce the notion of
![]() $\sigma $
-equivalence classes to tie together the alignment-free, noncrossing and nonnesting elements. These equivalence classes turn out to be intervals with respect to the quasiparabolic order on X, and the set
$\sigma $
-equivalence classes to tie together the alignment-free, noncrossing and nonnesting elements. These equivalence classes turn out to be intervals with respect to the quasiparabolic order on X, and the set
![]() $X_I$
of alignment-free elements form the top class with respect to a natural partial order. Any set of
$X_I$
of alignment-free elements form the top class with respect to a natural partial order. Any set of
![]() $\sigma $
-equivalence class representatives forms a basis of the Macdonald representation, and the change of basis matrices between any pair of such bases, including the noncrossing and nonnesting bases, are unitriangular (Theorem 5.16).
$\sigma $
-equivalence class representatives forms a basis of the Macdonald representation, and the change of basis matrices between any pair of such bases, including the noncrossing and nonnesting bases, are unitriangular (Theorem 5.16).
Throughout the rest of this section, we assume that we are working with a Weyl group W of rank n and type
![]() $E_7, E_8$
or
$E_7, E_8$
or
![]() $D_n$
for n even. All results hold independently of the rank and type of W, and we shall omit the statement of the above assumption except in the main theorems. We define the sum of each positive n-root
$D_n$
for n even. All results hold independently of the rank and type of W, and we shall omit the statement of the above assumption except in the main theorems. We define the sum of each positive n-root
![]() $\gamma $
to be the sum of the components of
$\gamma $
to be the sum of the components of
![]() $\gamma $
, and we denote it by
$\gamma $
, and we denote it by
![]() $\sigma (\gamma )$
.
$\sigma (\gamma )$
.
5.1 Alignment-free elements
Recall from Proposition 4.11 that W has a unique positive n-root
![]() $\theta _N$
that avoids both alignments and crossings. We will use
$\theta _N$
that avoids both alignments and crossings. We will use
![]() $\theta _N$
to help study general alignment-free elements.
$\theta _N$
to help study general alignment-free elements.
Proposition 5.1. Let
![]() $\theta _N$
be the unique positive n-root of type
$\theta _N$
be the unique positive n-root of type
![]() $N^M$
.
$N^M$
.
-
(i) A noncrossing n-root (i.e., one of type
 $A^pN^r$
) has a simple component.
$A^pN^r$
) has a simple component. -
(ii) The n-root
 $\theta _N$
has a unique simple component,
$\theta _N$
has a unique simple component,
 $\alpha _x$
.
$\alpha _x$
. -
(iii) If
 $\alpha _i$
is a simple root, then
$\alpha _i$
is a simple root, then
 $B(\sigma (\theta _N),\alpha _i)\ge 0$
, where equality holds if and only if
$B(\sigma (\theta _N),\alpha _i)\ge 0$
, where equality holds if and only if
 $\alpha _i\neq \alpha _x$
.
$\alpha _i\neq \alpha _x$
. -
(iv) Let
 $W_I$
be the parabolic subgroup of W generated by the set
$W_I$
be the parabolic subgroup of W generated by the set
 $S \backslash \{\alpha _x\}$
. Then the stabilizer of
$S \backslash \{\alpha _x\}$
. Then the stabilizer of
 $\sigma (\theta _N)$
is precisely
$\sigma (\theta _N)$
is precisely
 $W_I$
, and we have
$W_I$
, and we have
 $B(\sigma (\theta _N), \alpha _i) \geq 0$
for all simple roots
$B(\sigma (\theta _N), \alpha _i) \geq 0$
for all simple roots
 $\alpha _i$
.
$\alpha _i$
.
Proof. Let
![]() $\gamma $
be a noncrossing n-root of type
$\gamma $
be a noncrossing n-root of type
![]() $A^pN^r$
, and let R be the set of components of
$A^pN^r$
, and let R be the set of components of
![]() $\gamma $
. Assume for a contradiction that R contains no simple root, and let
$\gamma $
. Assume for a contradiction that R contains no simple root, and let
![]() $\beta $
be a root of minimal height in R. The bilinear form B has the property that
$\beta $
be a root of minimal height in R. The bilinear form B has the property that
![]() $B(\alpha ,\alpha ')\in \{-2,-1,0,1,2\}$
for any roots
$B(\alpha ,\alpha ')\in \{-2,-1,0,1,2\}$
for any roots
![]() $\alpha ,\alpha '$
, with
$\alpha ,\alpha '$
, with
![]() $B(\alpha ,\alpha ')=2$
if and only if
$B(\alpha ,\alpha ')=2$
if and only if
![]() $\alpha =\alpha '$
. Furthermore, for any positive root
$\alpha =\alpha '$
. Furthermore, for any positive root
![]() $\alpha $
, there exists a simple root
$\alpha $
, there exists a simple root
![]() $\alpha _i$
such that
$\alpha _i$
such that
![]() $B(\alpha ,\alpha _i)>0$
[Reference Humphreys33, Theorem 1.5]. It follows that there exists a simple root
$B(\alpha ,\alpha _i)>0$
[Reference Humphreys33, Theorem 1.5]. It follows that there exists a simple root
![]() $\alpha _i$
such that
$\alpha _i$
such that
![]() $B(\beta , \alpha _i) = 1$
.
$B(\beta , \alpha _i) = 1$
.
Since
![]() $\alpha _i$
is not in R, it moves a coplanar quadruple
$\alpha _i$
is not in R, it moves a coplanar quadruple
![]() $Q\subseteq R$
, and we have
$Q\subseteq R$
, and we have
![]() $\beta \in Q$
since
$\beta \in Q$
since
![]() $B(\beta ,\alpha _i)\neq 0$
. Let
$B(\beta ,\alpha _i)\neq 0$
. Let
![]() $\Psi $
be the
$\Psi $
be the
![]() $D_4$
-subsystem associated to Q. By hypothesis, Q is either an alignment or a nesting, and
$D_4$
-subsystem associated to Q. By hypothesis, Q is either an alignment or a nesting, and
![]() $\beta $
is an element of Q of minimal height. It follows from the explicit description of the sets
$\beta $
is an element of Q of minimal height. It follows from the explicit description of the sets
![]() $\Psi ^+_A=\Psi ^+_3$
and
$\Psi ^+_A=\Psi ^+_3$
and
![]() $\Psi ^+_N=\Psi ^+_2$
in the proof of Theorem 3.10 that
$\Psi ^+_N=\Psi ^+_2$
in the proof of Theorem 3.10 that
![]() $\beta $
is a root in the induced simple system of
$\beta $
is a root in the induced simple system of
![]() $\Psi $
. However, since
$\Psi $
. However, since
![]() $\alpha _i$
is simple root of W,
$\alpha _i$
is simple root of W,
![]() $\alpha _i$
is also in this induced simple system. This is a contradiction because we cannot have
$\alpha _i$
is also in this induced simple system. This is a contradiction because we cannot have
![]() $B(\gamma _1, \gamma _2)> 0$
for two simple roots
$B(\gamma _1, \gamma _2)> 0$
for two simple roots
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma _2$
in a root system. This completes the proof of (i).
$\gamma _2$
in a root system. This completes the proof of (i).
Now suppose further that
![]() $\gamma =\theta _N$
. It follows from (i) that R contains a simple root, so assume for a contradiction that R contains two simple roots,
$\gamma =\theta _N$
. It follows from (i) that R contains a simple root, so assume for a contradiction that R contains two simple roots,
![]() $\alpha _x$
and
$\alpha _x$
and
![]() $\alpha _y$
. Let P be a path from x to y in the Dynkin diagram
$\alpha _y$
. Let P be a path from x to y in the Dynkin diagram
![]() $\Gamma $
, and let
$\Gamma $
, and let
![]() $\beta $
be the root
$\beta $
be the root
![]() $\sum _{p \in P} \alpha _p$
. Note that
$\sum _{p \in P} \alpha _p$
. Note that
![]() $B(\beta , \alpha _x) = B(\beta , \alpha _y) = 1$
, so that
$B(\beta , \alpha _x) = B(\beta , \alpha _y) = 1$
, so that
![]() $\alpha _x$
and
$\alpha _x$
and
![]() $\alpha _y$
are both elements of the coplanar quadruple Q consisting of the roots moved by
$\alpha _y$
are both elements of the coplanar quadruple Q consisting of the roots moved by
![]() $\beta $
. Let
$\beta $
. Let
![]() $\Psi $
be the
$\Psi $
be the
![]() $D_4$
-subsystem associated with Q. Then
$D_4$
-subsystem associated with Q. Then
![]() $\alpha _i,\alpha _j$
are both induced simple roots of
$\alpha _i,\alpha _j$
are both induced simple roots of
![]() $\Psi $
since they are simple roots of W. However, the type of R is
$\Psi $
since they are simple roots of W. However, the type of R is
![]() $N^M$
, so Q is a nesting and thus contains a unique minimal root by the description of the set
$N^M$
, so Q is a nesting and thus contains a unique minimal root by the description of the set
![]() $\Psi ^+_N=\Psi ^+_2$
in the proof of Theorem 3.10. This is a contradiction, and (ii) follows.
$\Psi ^+_N=\Psi ^+_2$
in the proof of Theorem 3.10. This is a contradiction, and (ii) follows.
To prove (iii), let
![]() ${\alpha _i}$
be a simple root. If
${\alpha _i}$
be a simple root. If
![]() $\alpha _i = \alpha _x$
, then
$\alpha _i = \alpha _x$
, then
![]() $\alpha _x$
is a component of
$\alpha _x$
is a component of
![]() $\theta _N$
and we have
$\theta _N$
and we have
If
![]() $\alpha _i \ne \alpha _x$
, then
$\alpha _i \ne \alpha _x$
, then
![]() $\alpha _i$
is not a component of
$\alpha _i$
is not a component of
![]() $\theta _N$
, and Proposition 4.7 (i) implies that
$\theta _N$
, and Proposition 4.7 (i) implies that
![]() $\alpha _i$
moves an N to a C. Corollary 4.9 (ii) then implies that
$\alpha _i$
moves an N to a C. Corollary 4.9 (ii) then implies that
Equation 2.1 implies that
![]() $B(\alpha _i, \sigma (\theta _N))\ge 0$
for all i, with equality holding if and only if
$B(\alpha _i, \sigma (\theta _N))\ge 0$
for all i, with equality holding if and only if
![]() $\alpha _i\neq \alpha _x$
.
$\alpha _i\neq \alpha _x$
.
Part (iv) follows from (iii) by [Reference Humphreys33, Theorem 1.12 (a)], which says that the stabilizer of
![]() $\sigma (\theta _N)$
in W is generated by the simple reflections it contains.
$\sigma (\theta _N)$
in W is generated by the simple reflections it contains.
Proposition 5.2. Let
![]() $\theta _N$
be the unique positive n-root of type
$\theta _N$
be the unique positive n-root of type
![]() $N^M$
, let
$N^M$
, let
![]() $\alpha _x$
be the unique simple component of
$\alpha _x$
be the unique simple component of
![]() $\theta _N$
, and let
$\theta _N$
, and let
![]() $W_I$
be the parabolic subgroup of W generated by the set
$W_I$
be the parabolic subgroup of W generated by the set
![]() $S \backslash \{\alpha _x\}$
.
$S \backslash \{\alpha _x\}$
.
-
(i) The
 $W_I$
-orbit of positive n-roots that contains
$W_I$
-orbit of positive n-roots that contains
 $\theta _N$
is a quasiparabolic set
$\theta _N$
is a quasiparabolic set
 $(X_I, \lambda _I)$
for
$(X_I, \lambda _I)$
for
 $W_I$
, where
$W_I$
, where
 $\lambda _I$
is the restriction of
$\lambda _I$
is the restriction of
 $\lambda $
to
$\lambda $
to
 $X_I$
.
$X_I$
. -
(ii) The following are equivalent for a positive n-root
 $\beta $
:
$\beta $
:-
(1)
 $\beta $
has type
$\beta $
has type
 $C^q N^r$
for some q and r;
$C^q N^r$
for some q and r; -
(2)
 $\sigma (\beta ) = \sigma (\theta _N)$
;
$\sigma (\beta ) = \sigma (\theta _N)$
; -
(3)
 $\beta $
is an element of
$\beta $
is an element of
 $X_I$
.
$X_I$
.
In particular, the elements of the quasiparabolic set
 $X_I$
are precisely the alignment-free positive n-roots.
$X_I$
are precisely the alignment-free positive n-roots. -
-
(iii) There is a unique positive n-root,
 $\theta _C$
, of type
$\theta _C$
, of type
 $C^M$
, and it corresponds to the unique W-minimal element of the quasiparabolic set
$C^M$
, and it corresponds to the unique W-minimal element of the quasiparabolic set
 $X_I$
.
$X_I$
. -
(iv) If
 $\alpha $
is a root of
$\alpha $
is a root of
 $W_I$
and
$W_I$
and
 $\beta $
is an n-root in
$\beta $
is an n-root in
 $X_I$
whose components do not contain
$X_I$
whose components do not contain
 $\pm \alpha $
, then
$\pm \alpha $
, then
 $\lambda (s_\alpha (\beta )) = \lambda (\beta ) + 1\ \mod 2$
.
$\lambda (s_\alpha (\beta )) = \lambda (\beta ) + 1\ \mod 2$
.
Proof. Part (i) follows from Theorem 4.5 by restriction.
We now prove the implication (1)
![]() $\Rightarrow $
(2) of part (ii). Let
$\Rightarrow $
(2) of part (ii). Let
![]() $\beta $
be an n-root of type
$\beta $
be an n-root of type
![]() $C^q N^r$
. If
$C^q N^r$
. If
![]() $q = 0$
, then
$q = 0$
, then
![]() $\beta =\theta _N$
by Proposition 4.11 (ii) and (2) follows immediately, so suppose that
$\beta =\theta _N$
by Proposition 4.11 (ii) and (2) follows immediately, so suppose that
![]() $q> 0$
. By Remark 3.12 and Proposition 4.7 (iii), there exists a reflection
$q> 0$
. By Remark 3.12 and Proposition 4.7 (iii), there exists a reflection
![]() $\alpha $
that moves a crossing to a nesting in such a way that the n-root
$\alpha $
that moves a crossing to a nesting in such a way that the n-root
![]() $\beta ' = s_{\alpha }(\beta )$
has type
$\beta ' = s_{\alpha }(\beta )$
has type
![]() $C^{q-1}N^{r+1}$
. Corollary 4.9 (ii) proves that
$C^{q-1}N^{r+1}$
. Corollary 4.9 (ii) proves that
![]() $\sigma (\beta ') = \sigma (\beta )$
. It now follows from induction on q that
$\sigma (\beta ') = \sigma (\beta )$
. It now follows from induction on q that
![]() $\sigma (\beta ) = \sigma (\theta _N)$
, proving (2).
$\sigma (\beta ) = \sigma (\theta _N)$
, proving (2).
To prove (2)
![]() $\Rightarrow $
(3), assume that
$\Rightarrow $
(3), assume that
![]() $\sigma (\beta ) = \sigma (\theta _N)$
. By Lemma 3.2, there exists
$\sigma (\beta ) = \sigma (\theta _N)$
. By Lemma 3.2, there exists
![]() $w \in W$
such that
$w \in W$
such that
![]() $w(\theta _N) = \beta $
, so we have
$w(\theta _N) = \beta $
, so we have
It follows that
![]() $w \in W_I$
and
$w \in W_I$
and
![]() $\beta \in X_I$
, which proves (3).
$\beta \in X_I$
, which proves (3).
To prove (3)
![]() $\Rightarrow $
(1), let
$\Rightarrow $
(1), let
![]() $ \beta = w(\theta _N)$
for some
$ \beta = w(\theta _N)$
for some
![]() $w\in W_I$
and let
$w\in W_I$
and let
![]() $w= s_{i_1}s_{i_2} \cdots s_{i_k}$
be a reduced word of w. Then each simple reflection
$w= s_{i_1}s_{i_2} \cdots s_{i_k}$
be a reduced word of w. Then each simple reflection
![]() $s_{i_j}$
fixes
$s_{i_j}$
fixes
![]() $\sigma (\theta _N)$
, so it follows from Corollary 4.9 (ii) that
$\sigma (\theta _N)$
, so it follows from Corollary 4.9 (ii) that
![]() $s_{i_j}$
is a
$s_{i_j}$
is a
![]() $CN$
or
$CN$
or
![]() $NC$
move. It follows from Proposition 4.7 (i) that
$NC$
move. It follows from Proposition 4.7 (i) that
![]() $\beta $
has type
$\beta $
has type
![]() $C^q N^r$
, which implies (1) and completes the proof of (ii).
$C^q N^r$
, which implies (1) and completes the proof of (ii).
To prove (iii), note that the quasiparabolic set
![]() $X_I$
is finite and transitive, so it follows, as in the proof of Proposition 4.11 (i), that
$X_I$
is finite and transitive, so it follows, as in the proof of Proposition 4.11 (i), that
![]() $X_I$
has a unique minimal element (with respect to the quasiparabolic order) – namely, the unique element having minimal level in
$X_I$
has a unique minimal element (with respect to the quasiparabolic order) – namely, the unique element having minimal level in
![]() $X_I$
. The elements of
$X_I$
. The elements of
![]() $X_I$
are all of type
$X_I$
are all of type
![]() $C^qN^r$
by (ii) where
$C^qN^r$
by (ii) where
![]() $q+r=M$
and M is as in Corollary 3.19, so we have
$q+r=M$
and M is as in Corollary 3.19, so we have
![]() $\lambda _I(\gamma )\ge M$
for any element
$\lambda _I(\gamma )\ge M$
for any element
![]() $\gamma \in X_I$
, with equality holding if and only if
$\gamma \in X_I$
, with equality holding if and only if
![]() $\gamma $
has type
$\gamma $
has type
![]() $C^M$
. To prove (iii), it now remains to show that such an element exists.
$C^M$
. To prove (iii), it now remains to show that such an element exists.
Let
![]() $\beta $
be an n-root in
$\beta $
be an n-root in
![]() $X_I$
, and suppose
$X_I$
, and suppose
![]() $\beta $
has type
$\beta $
has type
![]() $C^q N^r$
where
$C^q N^r$
where
![]() $r> 0$
. Then
$r> 0$
. Then
![]() $\sigma (\beta )=\sigma (\theta _N)$
, and
$\sigma (\beta )=\sigma (\theta _N)$
, and
![]() $\beta $
admits an
$\beta $
admits an
![]() $NC$
move by a reflection
$NC$
move by a reflection
![]() $s_\alpha $
corresponding to some root
$s_\alpha $
corresponding to some root
![]() $\alpha $
. Theorem 3.10 (vi) implies that
$\alpha $
. Theorem 3.10 (vi) implies that
![]() $\sigma (s_{\alpha }(\beta )) = \sigma (\beta )=\sigma (\theta _N)$
, so
$\sigma (s_{\alpha }(\beta )) = \sigma (\beta )=\sigma (\theta _N)$
, so
![]() $s_\alpha (\beta )$
is in
$s_\alpha (\beta )$
is in
![]() $X_I$
and has type
$X_I$
and has type
![]() $C^a N^b$
by (ii). Proposition 4.7 (iii) implies that
$C^a N^b$
by (ii). Proposition 4.7 (iii) implies that
![]() $a> q$
and
$a> q$
and
![]() $b < r$
, and that
$b < r$
, and that
![]() $s_\alpha (\beta )$
has a lower level than
$s_\alpha (\beta )$
has a lower level than
![]() $\beta $
. It follows that
$\beta $
. It follows that
![]() $X_I$
has an element of type
$X_I$
has an element of type
![]() $C^M$
, which completes the proof of (iii).
$C^M$
, which completes the proof of (iii).
Suppose that
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are as in the statement of (iv). Since neither of
$\beta $
are as in the statement of (iv). Since neither of
![]() $\pm \alpha $
is a component of
$\pm \alpha $
is a component of
![]() $\beta $
, the reflection
$\beta $
, the reflection
![]() $s_\alpha $
must move a C to an N or vice versa by Remark 3.12 and (ii). Proposition 4.7 (iii) then implies that
$s_\alpha $
must move a C to an N or vice versa by Remark 3.12 and (ii). Proposition 4.7 (iii) then implies that
![]() $\lambda (\beta )$
and
$\lambda (\beta )$
and
![]() $\lambda (s_\alpha (\beta ))$
have opposite parities.
$\lambda (s_\alpha (\beta ))$
have opposite parities.
Remark 5.3. With some work, it can be shown that the positive n-roots in
![]() $X_I$
are also exactly the positive n-roots
$X_I$
are also exactly the positive n-roots
![]() $\beta $
with the property that every component
$\beta $
with the property that every component
![]() $\alpha $
of
$\alpha $
of
![]() $\beta $
has x-height 1, in the sense that
$\beta $
has x-height 1, in the sense that
![]() $\alpha $
expands into a linear combination of simple roots where the simple root
$\alpha $
expands into a linear combination of simple roots where the simple root
![]() $\alpha _x$
appears with coefficient
$\alpha _x$
appears with coefficient
![]() $1$
. Since the simple roots of
$1$
. Since the simple roots of
![]() $W_I$
do not include
$W_I$
do not include
![]() $\alpha _x$
, it follows that no root of
$\alpha _x$
, it follows that no root of
![]() $W_I$
divides any n-root in
$W_I$
divides any n-root in
![]() $X_I$
. In other words, the ‘if’ condition in Proposition 5.2 (iv) in fact holds for every root
$X_I$
. In other words, the ‘if’ condition in Proposition 5.2 (iv) in fact holds for every root
![]() $\alpha $
of
$\alpha $
of
![]() $W_I$
and every n-root
$W_I$
and every n-root
![]() $\beta \in X_I$
. This implies that the sets of all n-roots in
$\beta \in X_I$
. This implies that the sets of all n-roots in
![]() $X_I$
with even levels and of all n-roots in
$X_I$
with even levels and of all n-roots in
![]() $X_I$
with odd levels are interchanged by
$X_I$
with odd levels are interchanged by
![]() $s_\alpha $
for every
$s_\alpha $
for every
![]() $\alpha \in W_I$
. In particular, these two sets have the same cardinality.
$\alpha \in W_I$
. In particular, these two sets have the same cardinality.
5.2 Two bases
The goal of this subsection is to prove that the noncrossing n-roots and the nonnesting n-roots each form a basis for the Macdonald representation
![]() $j^{\Phi }_{nA_1}({\mathrm {sgn}})$
. The proof is based on a commutative version of Bergman’s diamond lemma [Reference Bergman5], which is a special case of Newman’s diamond lemma [Reference Newman41]. We define the crossing order,
$j^{\Phi }_{nA_1}({\mathrm {sgn}})$
. The proof is based on a commutative version of Bergman’s diamond lemma [Reference Bergman5], which is a special case of Newman’s diamond lemma [Reference Newman41]. We define the crossing order,
![]() $\leq _C$
, on the set of positive n-roots by declaring that
$\leq _C$
, on the set of positive n-roots by declaring that
![]() $\beta \leq _C \gamma $
if either
$\beta \leq _C \gamma $
if either
![]() $\sigma (\beta ) < \sigma (\gamma )$
, or both
$\sigma (\beta ) < \sigma (\gamma )$
, or both
![]() $\sigma (\beta ) = \sigma (\gamma )$
and
$\sigma (\beta ) = \sigma (\gamma )$
and
![]() $\beta \geq _Q \gamma $
, where
$\beta \geq _Q \gamma $
, where
![]() $\leq _Q$
is the quasiparabolic order. Similarly, we define the nesting order,
$\leq _Q$
is the quasiparabolic order. Similarly, we define the nesting order,
![]() $\leq _N$
, on the set of positive n-roots by declaring that
$\leq _N$
, on the set of positive n-roots by declaring that
![]() $\beta \leq _N \gamma $
if either
$\beta \leq _N \gamma $
if either
![]() $\sigma (\beta ) < \sigma (\gamma )$
(with respect to the order
$\sigma (\beta ) < \sigma (\gamma )$
(with respect to the order
![]() $\le $
on roots), or both
$\le $
on roots), or both
![]() $\sigma (\beta ) = \sigma (\gamma )$
and
$\sigma (\beta ) = \sigma (\gamma )$
and
![]() $\beta \leq _Q \gamma $
.
$\beta \leq _Q \gamma $
.
Given any relation of the form
![]() $\gamma \gamma _C = \gamma \gamma _N + \gamma \gamma _A$
among three n-roots in the setting of Theorem 3.10 (where
$\gamma \gamma _C = \gamma \gamma _N + \gamma \gamma _A$
among three n-roots in the setting of Theorem 3.10 (where
![]() $\gamma _C, \gamma _N$
and
$\gamma _C, \gamma _N$
and
![]() $\gamma _A$
are the crossing, nesting and alignment corresponding to the same type-
$\gamma _A$
are the crossing, nesting and alignment corresponding to the same type-
![]() $D_4$
subsystem of the root system of W, respectively), we have
$D_4$
subsystem of the root system of W, respectively), we have
![]() $\gamma \gamma _A<_C\gamma \gamma _C$
and
$\gamma \gamma _A<_C\gamma \gamma _C$
and
![]() $\gamma \gamma _A<_N\gamma \gamma _N$
because
$\gamma \gamma _A<_N\gamma \gamma _N$
because
![]() $\sigma (\gamma _A)<\sigma (\gamma _C)=\sigma (\gamma _N)$
by Theorem 3.10 (vi). We also have
$\sigma (\gamma _A)<\sigma (\gamma _C)=\sigma (\gamma _N)$
by Theorem 3.10 (vi). We also have
![]() $\gamma _C<_N \gamma _N$
and
$\gamma _C<_N \gamma _N$
and
![]() $\gamma _N <_C \gamma _C$
by Proposition 4.7 (iii) and the definition of
$\gamma _N <_C \gamma _C$
by Proposition 4.7 (iii) and the definition of
![]() $\le _Q$
, because for any component
$\le _Q$
, because for any component
![]() $\alpha $
of
$\alpha $
of
![]() $\theta _A$
, the reflection
$\theta _A$
, the reflection
![]() $s_\alpha $
moves the components of
$s_\alpha $
moves the components of
![]() $\gamma _C$
to those of
$\gamma _C$
to those of
![]() $\gamma _N$
by Theorem 3.10 (vi). It also follows that
$\gamma _N$
by Theorem 3.10 (vi). It also follows that
![]() $\lambda (\gamma \gamma _C)< \lambda (\gamma \gamma _N)$
and
$\lambda (\gamma \gamma _C)< \lambda (\gamma \gamma _N)$
and
![]() $\gamma \gamma _C \leq _Q \gamma \gamma _N$
. We may therefore regard the relations
$\gamma \gamma _C \leq _Q \gamma \gamma _N$
. We may therefore regard the relations
![]() $\gamma \gamma _C = \gamma \gamma _N + \gamma \gamma _A$
as directed reduction rules, each of which operates on a single term
$\gamma \gamma _C = \gamma \gamma _N + \gamma \gamma _A$
as directed reduction rules, each of which operates on a single term
![]() $\lambda _i \beta _i$
in a linear combination
$\lambda _i \beta _i$
in a linear combination
![]() $\sum _i \lambda _i \beta _i$
, where the
$\sum _i \lambda _i \beta _i$
, where the
![]() $\beta _i$
are positive n-roots. Each reduction rule can be used either (a) to express a positive n-root
$\beta _i$
are positive n-roots. Each reduction rule can be used either (a) to express a positive n-root
![]() $\gamma \gamma _C$
containing a crossing as the sum of two other positive n-roots
$\gamma \gamma _C$
containing a crossing as the sum of two other positive n-roots
![]() $\gamma \gamma _A, \gamma \gamma _N$
that are strictly lower than it in the crossing order, or (b) to express a positive n-root
$\gamma \gamma _A, \gamma \gamma _N$
that are strictly lower than it in the crossing order, or (b) to express a positive n-root
![]() $\gamma \gamma _N$
containing a nesting as a linear combination of two other positive n-roots
$\gamma \gamma _N$
containing a nesting as a linear combination of two other positive n-roots
![]() $\gamma \gamma _A,\gamma \gamma _C$
that are strictly lower than it in the nesting order.
$\gamma \gamma _A,\gamma \gamma _C$
that are strictly lower than it in the nesting order.
In order to apply the diamond lemma, we need to know (a) that it is never possible to apply an infinite sequence of reduction rules to a linear combination of n-roots, and (b) that the reduction rules are confluent. The latter condition means that if m is a linear combination of n-roots and if
![]() $f_1$
and
$f_1$
and
![]() $f_2$
are two different reductions that can be applied to m, then the linear combinations
$f_2$
are two different reductions that can be applied to m, then the linear combinations
![]() $f_1(m)$
and
$f_1(m)$
and
![]() $f_2(m)$
themselves have a common reduction,
$f_2(m)$
themselves have a common reduction,
![]() $m'$
. In other words, it is possible to reduce
$m'$
. In other words, it is possible to reduce
![]() $f_1(m)$
to
$f_1(m)$
to
![]() $m'$
by applying a suitable sequence of reductions, and it is possible to reduce
$m'$
by applying a suitable sequence of reductions, and it is possible to reduce
![]() $f_2(m)$
to the same
$f_2(m)$
to the same
![]() $m'$
by applying a possibly different sequence of reductions. If these two conditions hold, the conclusion of the diamond lemma is that every element of the module may be uniquely expressed as an element to which no reduction rules may be applied – in other words, a unique linear combination of noncrossing n-roots, or a unique linear combination of nonnesting n-roots.
$m'$
by applying a possibly different sequence of reductions. If these two conditions hold, the conclusion of the diamond lemma is that every element of the module may be uniquely expressed as an element to which no reduction rules may be applied – in other words, a unique linear combination of noncrossing n-roots, or a unique linear combination of nonnesting n-roots.
Conversely, the diamond lemma guarantees that if each element m can be uniquely expressed as a linear combination of nonnesting (or noncrossing) n-roots, then the reduction relations are confluent.
Lemma 5.4. There are
![]() $2$
nonnesting positive
$2$
nonnesting positive
![]() $4$
-roots in type
$4$
-roots in type
![]() $D_4$
, and
$D_4$
, and
![]() $5$
nonnesting positive
$5$
nonnesting positive
![]() $6$
-roots in type
$6$
-roots in type
![]() $D_6$
. The nonnesting positive n-roots are linearly independent in the Macdonald representation
$D_6$
. The nonnesting positive n-roots are linearly independent in the Macdonald representation
![]() $j^{\Phi }_{nA_1}({\mathrm {sgn}})$
in each case.
$j^{\Phi }_{nA_1}({\mathrm {sgn}})$
in each case.
Proof. In type
![]() $D_4$
, the set in question is
$D_4$
, the set in question is
![]() $\{(\varepsilon _1^2-\varepsilon _2^2)(\varepsilon _3^2-\varepsilon _4^2),\ (\varepsilon _1^2-\varepsilon _3^2)(\varepsilon _2^2-\varepsilon _4^2)\}$
, which is clearly linearly independent. In type
$\{(\varepsilon _1^2-\varepsilon _2^2)(\varepsilon _3^2-\varepsilon _4^2),\ (\varepsilon _1^2-\varepsilon _3^2)(\varepsilon _2^2-\varepsilon _4^2)\}$
, which is clearly linearly independent. In type
![]() $D_6$
, the nonnesting positive
$D_6$
, the nonnesting positive
![]() $6$
-roots correspond to the matchings
$6$
-roots correspond to the matchings
One can check that this set is linearly independent by comparing coefficients of
![]() $\varepsilon _1^2 \varepsilon _2^2 \varepsilon _3^2$
,
$\varepsilon _1^2 \varepsilon _2^2 \varepsilon _3^2$
,
![]() $\varepsilon _1^2 \varepsilon _2^2 \varepsilon _4^2$
,
$\varepsilon _1^2 \varepsilon _2^2 \varepsilon _4^2$
,
![]() $\varepsilon _1^2 \varepsilon _2^2 \varepsilon _5^2$
,
$\varepsilon _1^2 \varepsilon _2^2 \varepsilon _5^2$
,
![]() $\varepsilon _1^2 \varepsilon _3^2 \varepsilon _4^2$
and
$\varepsilon _1^2 \varepsilon _3^2 \varepsilon _4^2$
and
![]() $\varepsilon _1^2 \varepsilon _3^2 \varepsilon _5^2$
.
$\varepsilon _1^2 \varepsilon _3^2 \varepsilon _5^2$
.
Theorem 5.5. Let W be a Weyl group of type
![]() $E_7$
,
$E_7$
,
![]() $E_8$
or
$E_8$
or
![]() $D_n$
for n even. Let
$D_n$
for n even. Let
![]() $j^{\Phi }_{nA_1}({\mathrm {sgn}})$
be the Macdonald representation of W.
$j^{\Phi }_{nA_1}({\mathrm {sgn}})$
be the Macdonald representation of W.
-
(i) The nonnesting positive n-roots form a
 ${\mathbb Q}$
-basis for
${\mathbb Q}$
-basis for
 $j^{\Phi }_{nA_1}({\mathrm {sgn}})$
.
$j^{\Phi }_{nA_1}({\mathrm {sgn}})$
. -
(ii) The noncrossing positive n-roots form a
 ${\mathbb Q}$
-basis for
${\mathbb Q}$
-basis for
 $j^{\Phi }_{nA_1}({\mathrm {sgn}})$
.
$j^{\Phi }_{nA_1}({\mathrm {sgn}})$
. -
(iii) The alignment-free positive n-roots span
 $j^{\Phi }_{nA_1}({\mathrm {sgn}})$
.
$j^{\Phi }_{nA_1}({\mathrm {sgn}})$
.
Proof. We first prove (i) by using the reduction rule
![]() $\gamma \gamma _N = \gamma \gamma _C - \gamma \gamma _A$
of Theorem 3.10 (vi) to express an n-root that contains a nesting as a linear combination of n-roots that are strictly lower in the nesting order. There are no infinite descending chains in the crossing order because there are only finitely many n-roots. It remains to show that the reductions
$\gamma \gamma _N = \gamma \gamma _C - \gamma \gamma _A$
of Theorem 3.10 (vi) to express an n-root that contains a nesting as a linear combination of n-roots that are strictly lower in the nesting order. There are no infinite descending chains in the crossing order because there are only finitely many n-roots. It remains to show that the reductions
![]() $f_i$
are confluent, by induction on the rank n. By Lemma 5.4, this is already known to be the case in types
$f_i$
are confluent, by induction on the rank n. By Lemma 5.4, this is already known to be the case in types
![]() $D_4$
and
$D_4$
and
![]() $D_6$
, so we assume from now on that we have
$D_6$
, so we assume from now on that we have
![]() $n> 6$
.
$n> 6$
.
If two reductions,
![]() $f_i$
and
$f_i$
and
![]() $f_j$
, affect different terms
$f_j$
, affect different terms
![]() $\lambda _i \beta _i$
in the linear combination
$\lambda _i \beta _i$
in the linear combination
![]() $m = \sum _i \lambda _i \beta _i$
, or if
$m = \sum _i \lambda _i \beta _i$
, or if
![]() $f_i$
and
$f_i$
and
![]() $f_j$
affect disjoint components of the same term
$f_j$
affect disjoint components of the same term
![]() $\lambda _i \beta _i$
, then
$\lambda _i \beta _i$
, then
![]() $f_i$
and
$f_i$
and
![]() $f_j$
commute. It is then immediate that
$f_j$
commute. It is then immediate that
![]() $f_i(m)$
and
$f_i(m)$
and
![]() $f_j(m)$
have a common reduction – namely,
$f_j(m)$
have a common reduction – namely,
![]() $f_if_j(m) = f_jf_i(m)$
. The proof of confluence now reduces to proving that if
$f_if_j(m) = f_jf_i(m)$
. The proof of confluence now reduces to proving that if
![]() $f_i$
and
$f_i$
and
![]() $f_j$
change at least one component in the same n-root
$f_j$
change at least one component in the same n-root
![]() $\beta $
, then
$\beta $
, then
![]() $f_i(\beta )$
and
$f_i(\beta )$
and
![]() $f_j(\beta )$
have a common reduction. In this case, if
$f_j(\beta )$
have a common reduction. In this case, if
![]() $Q_i$
and
$Q_i$
and
![]() $Q_j$
are the sets of components of
$Q_j$
are the sets of components of
![]() $\beta $
that are moved by
$\beta $
that are moved by
![]() $f_i$
and
$f_i$
and
![]() $f_j$
respectively, then Proposition 3.20 (i) implies that either
$f_j$
respectively, then Proposition 3.20 (i) implies that either
![]() $Q_i = Q_j$
, or
$Q_i = Q_j$
, or
![]() $|Q_i \cap Q_j| = 2$
. In the first case, we have
$|Q_i \cap Q_j| = 2$
. In the first case, we have
![]() $f_i = f_j$
, and there is nothing to prove. In the latter case, Proposition 3.20 (ii) implies that there is a root subsystem
$f_i = f_j$
, and there is nothing to prove. In the latter case, Proposition 3.20 (ii) implies that there is a root subsystem
![]() $\Psi $
of type
$\Psi $
of type
![]() $D_6$
that contains
$D_6$
that contains
![]() $Q_i$
and
$Q_i$
and
![]() $Q_j$
as coplanar quadruples. Confluence now follows by applying the inductive hypothesis to
$Q_j$
as coplanar quadruples. Confluence now follows by applying the inductive hypothesis to
![]() $\Psi $
, which completes the proof of (i).
$\Psi $
, which completes the proof of (i).
We now prove (ii) by using the reduction rule
![]() $\gamma \gamma _C = \gamma \gamma _N + \gamma \gamma _A$
of Theorem 3.10 (vi) to express an n-root that contains a crossing as a sum of n-roots that are strictly lower in the crossing order
$\gamma \gamma _C = \gamma \gamma _N + \gamma \gamma _A$
of Theorem 3.10 (vi) to express an n-root that contains a crossing as a sum of n-roots that are strictly lower in the crossing order
![]() $\leq _C$
. It follows that the noncrossing positive n-roots form a spanning set. There are
$\leq _C$
. It follows that the noncrossing positive n-roots form a spanning set. There are
![]() $2$
noncrossing positive
$2$
noncrossing positive
![]() $4$
-roots in type
$4$
-roots in type
![]() $D_4$
, corresponding to the matchings
$D_4$
, corresponding to the matchings
![]() $\{12, 34\}$
and
$\{12, 34\}$
and
![]() $\{14,23\}$
, and
$\{14,23\}$
, and
![]() $5$
noncrossing positive
$5$
noncrossing positive
![]() $6$
-roots in type
$6$
-roots in type
![]() $D_6$
, corresponding to the matchings
$D_6$
, corresponding to the matchings
These spanning sets are bases of
![]() $j^{\Phi }_{nA_1}({\mathrm {sgn}})$
by (i), and the rest of the argument used to prove (i) now applies mutatis mutandis.
$j^{\Phi }_{nA_1}({\mathrm {sgn}})$
by (i), and the rest of the argument used to prove (i) now applies mutatis mutandis.
Part (iii) follows by expressing the reduction rule in the form
![]() $\gamma \gamma _A = \gamma \gamma _C - \gamma \gamma _N.$
By Theorem 3.10 (vi), we have
$\gamma \gamma _A = \gamma \gamma _C - \gamma \gamma _N.$
By Theorem 3.10 (vi), we have
![]() $\sigma (\gamma \gamma _A) < \sigma (\gamma \gamma _N) = \sigma (\gamma \gamma _C)$
. This implies that the relation can only be applied finitely many times before the procedure terminates, and (iii) follows.
$\sigma (\gamma \gamma _A) < \sigma (\gamma \gamma _N) = \sigma (\gamma \gamma _C)$
. This implies that the relation can only be applied finitely many times before the procedure terminates, and (iii) follows.
We will refer to the bases of nonnesting and noncrossing positive n-roots as the nonnesting basis and noncrossing basis of the Macdonald representation.
5.3 Properties of the noncrossing basis
In this subsection, we show that the noncrossing basis behaves in the Macdonald representation in many ways like a simple system in the reflection representation. In particular, every n-root decomposes into the noncrossing basis with coefficients of like sign, and the noncrossing n-roots are precisely the minimal ones that are minimal in the sense that they are not further decomposable. This minimality property yields an elementary algebraic characterization. We also show that the maximally crossing n-root
![]() $\theta _C$
has a maximal decomposition into the noncrossing basis in a natural sense, and that simple reflections act on the noncrossing basis in a way reminiscent of the way they act on a simple system in the reflection representation. In addition, as we explain in Remark 5.8, the noncrossing basis is a sign-coherence basis in the sense of cluster algebras, and it also essentially agrees with an IC basis in the sense of Du [Reference Du21]. For the above reasons, we may think of the noncrossing basis as the canonical basis of the Macdonald representation.
$\theta _C$
has a maximal decomposition into the noncrossing basis in a natural sense, and that simple reflections act on the noncrossing basis in a way reminiscent of the way they act on a simple system in the reflection representation. In addition, as we explain in Remark 5.8, the noncrossing basis is a sign-coherence basis in the sense of cluster algebras, and it also essentially agrees with an IC basis in the sense of Du [Reference Du21]. For the above reasons, we may think of the noncrossing basis as the canonical basis of the Macdonald representation.
Lemma 5.6. If
![]() $\beta $
and
$\beta $
and
![]() $\lambda \beta $
are both n-roots for some scalar
$\lambda \beta $
are both n-roots for some scalar
![]() $\lambda $
, then we must have
$\lambda $
, then we must have
![]() $\lambda = \pm 1$
.
$\lambda = \pm 1$
.
Proof. Theorem 5.5 implies that the scalar
![]() $\lambda $
in (ii) lies in
$\lambda $
in (ii) lies in
![]() ${\mathbb Q}$
. Lemma 3.2 implies that there exists
${\mathbb Q}$
. Lemma 3.2 implies that there exists
![]() $w \in W$
such that
$w \in W$
such that
![]() $w(\beta ) = \lambda \beta $
. Because w has finite order, it follows that
$w(\beta ) = \lambda \beta $
. Because w has finite order, it follows that
![]() $\lambda $
is a root of unity, and this forces
$\lambda $
is a root of unity, and this forces
![]() $\lambda =\pm 1$
.
$\lambda =\pm 1$
.
Theorem 5.7. Let W be a Weyl group of type
![]() $E_7$
,
$E_7$
,
![]() $E_8$
or
$E_8$
or
![]() $D_n$
for n even, and let
$D_n$
for n even, and let
![]() $\mathcal B$
be the set of noncrossing positive n-roots.
$\mathcal B$
be the set of noncrossing positive n-roots.
-
(i) Every n-root is a
 ${\mathbb Z}$
-linear combination of elements of
${\mathbb Z}$
-linear combination of elements of
 $\mathcal B$
, with coefficients of like sign. This sign is positive if the n-root is positive, and is negative if the n-root is negative.
$\mathcal B$
, with coefficients of like sign. This sign is positive if the n-root is positive, and is negative if the n-root is negative. -
(ii) A positive n-root is noncrossing if and only if it is not a positive linear combination of other positive n-roots.
-
(iii) Define
 $\gamma \le _{\mathcal B}\gamma '$
for positive n-roots
$\gamma \le _{\mathcal B}\gamma '$
for positive n-roots
 $\gamma =\sum _{\beta \in \mathcal B} c_\beta \beta $
and
$\gamma =\sum _{\beta \in \mathcal B} c_\beta \beta $
and
 $\gamma '=\sum _{\beta \in \mathcal B}c^{\prime }_\beta \beta $
whenever
$\gamma '=\sum _{\beta \in \mathcal B}c^{\prime }_\beta \beta $
whenever
 $c_\beta \leq d_\beta $
for all
$c_\beta \leq d_\beta $
for all
 $\beta \in \mathcal B$
. Then
$\beta \in \mathcal B$
. Then
 $\le _{\mathcal B}$
is a partial order on the set X of positive n-roots. The maximally crossing element
$\le _{\mathcal B}$
is a partial order on the set X of positive n-roots. The maximally crossing element
 $\theta _C$
is the unique maximal element of X with respect to
$\theta _C$
is the unique maximal element of X with respect to
 $\le _{\mathcal B}$
.
$\le _{\mathcal B}$
. -
(iv) If
 $\gamma \in \mathcal B$
and
$\gamma \in \mathcal B$
and
 $\alpha _i$
is a simple root, then we have
$\alpha _i$
is a simple root, then we have  $$ \begin{align*}s_{\alpha_i}(\gamma) = \begin{cases} -\gamma & \text{\ if\ } \alpha_i | \gamma;\\ \gamma + \gamma' & \text{\ otherwise,\ for\ some\ } \gamma' \in \mathcal B {\text{\ such\ that\ }} \alpha_i | \gamma'.\\ \end{cases}\end{align*} $$
$$ \begin{align*}s_{\alpha_i}(\gamma) = \begin{cases} -\gamma & \text{\ if\ } \alpha_i | \gamma;\\ \gamma + \gamma' & \text{\ otherwise,\ for\ some\ } \gamma' \in \mathcal B {\text{\ such\ that\ }} \alpha_i | \gamma'.\\ \end{cases}\end{align*} $$
Proof. Let
![]() $\beta $
be a positive n-root. By the proof of Theorem 5.5, the result of applying reductions of the form
$\beta $
be a positive n-root. By the proof of Theorem 5.5, the result of applying reductions of the form
![]() $\gamma \gamma _C = \gamma \gamma _N + \gamma \gamma _A$
to
$\gamma \gamma _C = \gamma \gamma _N + \gamma \gamma _A$
to
![]() $\beta $
until this is no longer possible has the effect of expressing
$\beta $
until this is no longer possible has the effect of expressing
![]() $\beta $
as a positive integer linear combination of noncrossing n-roots, and this procedure will always terminate after finitely many steps. This proves (i) for positive n-roots, and the statement for negative n-roots follows because n-roots occur in positive-negative pairs.
$\beta $
as a positive integer linear combination of noncrossing n-roots, and this procedure will always terminate after finitely many steps. This proves (i) for positive n-roots, and the statement for negative n-roots follows because n-roots occur in positive-negative pairs.
If
![]() $\beta $
is a positive n-root that contains a crossing, then
$\beta $
is a positive n-root that contains a crossing, then
![]() $\beta $
is a positive linear combination of other positive n-roots by applying the reduction rule in the first paragraph. Conversely, suppose that
$\beta $
is a positive linear combination of other positive n-roots by applying the reduction rule in the first paragraph. Conversely, suppose that
![]() $\beta $
is a noncrossing n-root and that
$\beta $
is a noncrossing n-root and that
![]() $\beta = \sum _i \lambda _i \beta _i$
, where
$\beta = \sum _i \lambda _i \beta _i$
, where
![]() $\lambda _i> 0$
and
$\lambda _i> 0$
and
![]() $\beta _i$
is a positive n-root that is different from
$\beta _i$
is a positive n-root that is different from
![]() $\beta $
for each i. Part (i) implies that each of the
$\beta $
for each i. Part (i) implies that each of the
![]() $\beta _i$
is a positive linear combination of noncrossing n-roots. Because no cancellation can occur in the sum, Theorem 5.5 (ii) implies that this is only possible if each
$\beta _i$
is a positive linear combination of noncrossing n-roots. Because no cancellation can occur in the sum, Theorem 5.5 (ii) implies that this is only possible if each
![]() $\beta _i$
is a multiple of
$\beta _i$
is a multiple of
![]() $\beta $
. Collecting terms, we then have
$\beta $
. Collecting terms, we then have
![]() $\beta = \lambda \beta _i$
. Lemma 5.6 and the assumption that
$\beta = \lambda \beta _i$
. Lemma 5.6 and the assumption that
![]() $\beta _i$
is positive then imply that
$\beta _i$
is positive then imply that
![]() $\lambda =1$
and
$\lambda =1$
and
![]() $\beta = \beta _i$
, which is a contradiction.
$\beta = \beta _i$
, which is a contradiction.
The relation
![]() $\le _{\mathcal B}$
in (iii) is clearly a partial order on X. Since X is finite, it contains at least one maximal positive n-root with respect to
$\le _{\mathcal B}$
in (iii) is clearly a partial order on X. Since X is finite, it contains at least one maximal positive n-root with respect to
![]() $\le $
. To prove (iii), it then suffices to show that for every n-root
$\le $
. To prove (iii), it then suffices to show that for every n-root
![]() $\gamma \in X$
not equal to
$\gamma \in X$
not equal to
![]() $\theta _C$
, there is an element
$\theta _C$
, there is an element
![]() $\gamma '\in X$
such that
$\gamma '\in X$
such that
![]() $\gamma <_{\mathcal B}\gamma '$
. Let
$\gamma <_{\mathcal B}\gamma '$
. Let
![]() $\gamma \in X$
be an n-root not equal to
$\gamma \in X$
be an n-root not equal to
![]() $\theta _C$
, so that we can factorize
$\theta _C$
, so that we can factorize
![]() $\gamma $
as
$\gamma $
as
![]() $\gamma _1 \gamma '$
, where
$\gamma _1 \gamma '$
, where
![]() $\gamma '$
is either an alignment or a nesting. In either case, Theorem 3.10 (vi) implies that there exists a reflection
$\gamma '$
is either an alignment or a nesting. In either case, Theorem 3.10 (vi) implies that there exists a reflection
![]() $s_\alpha $
such that
$s_\alpha $
such that
![]() $s_\alpha (\gamma ')$
is a crossing, and that we have
$s_\alpha (\gamma ')$
is a crossing, and that we have
![]() $s_\alpha (\gamma ') = \gamma ' + \gamma "$
, where
$s_\alpha (\gamma ') = \gamma ' + \gamma "$
, where
![]() $\gamma "$
is a nesting if
$\gamma "$
is a nesting if
![]() $\gamma '$
is an alignment, or vice versa. We then have
$\gamma '$
is an alignment, or vice versa. We then have
where
![]() $\gamma _1\gamma "$
is also a positive n-root. If we write the n-root
$\gamma _1\gamma "$
is also a positive n-root. If we write the n-root
![]() $s_\alpha (\gamma )$
as
$s_\alpha (\gamma )$
as
![]() $s_\alpha (\gamma ) = \sum _{\beta \in \mathcal B} e_\beta \beta $
, then it follows from (i) that
$s_\alpha (\gamma ) = \sum _{\beta \in \mathcal B} e_\beta \beta $
, then it follows from (i) that
![]() $c_\beta \leq e_\beta $
for all
$c_\beta \leq e_\beta $
for all
![]() $\beta \in \mathcal B$
. It follows that
$\beta \in \mathcal B$
. It follows that
![]() $\gamma <_{\mathcal B} s_\alpha (\gamma )$
, proving (iii).
$\gamma <_{\mathcal B} s_\alpha (\gamma )$
, proving (iii).
In the situation of (iv), it is immediate that if
![]() $\alpha _i$
is a component of
$\alpha _i$
is a component of
![]() $\gamma $
, then
$\gamma $
, then
![]() $s_{i}(\gamma ) = -\gamma $
. Suppose from now on that this is not the case, and let
$s_{i}(\gamma ) = -\gamma $
. Suppose from now on that this is not the case, and let
![]() $A^pN^r$
be the type of
$A^pN^r$
be the type of
![]() $\gamma $
. Let R be the set of components of
$\gamma $
. Let R be the set of components of
![]() $\gamma $
, let
$\gamma $
, let
![]() $Q\subseteq R$
be the coplanar quadruple moved by
$Q\subseteq R$
be the coplanar quadruple moved by
![]() $\alpha _{i}$
, and let
$\alpha _{i}$
, and let
![]() $\Psi $
be the
$\Psi $
be the
![]() $D_4$
-subsystem of Q. Then the sets
$D_4$
-subsystem of Q. Then the sets
![]() $Q, Q'=s_i(Q)$
and
$Q, Q'=s_i(Q)$
and
![]() $Q"=\Psi ^+\setminus (Q\cup Q')$
are the three distinct coplanar quadruples partitioning the induced positive system by Proposition 3.8 (ii) and Theorem 3.10. Let
$Q"=\Psi ^+\setminus (Q\cup Q')$
are the three distinct coplanar quadruples partitioning the induced positive system by Proposition 3.8 (ii) and Theorem 3.10. Let
![]() $\Psi ^+_A, \Psi ^+_C$
and
$\Psi ^+_A, \Psi ^+_C$
and
![]() $\Psi ^+_N$
be the alignment, crossing and nesting in
$\Psi ^+_N$
be the alignment, crossing and nesting in
![]() $\Psi ^+$
, respectively. Then since
$\Psi ^+$
, respectively. Then since
![]() $\alpha _i$
is a simple root, Proposition 4.7 (i) implies that we must have one of the following two situations:
$\alpha _i$
is a simple root, Proposition 4.7 (i) implies that we must have one of the following two situations:
-
(1)
 $Q=\Psi ^+_A$
,
$Q=\Psi ^+_A$
,
 $Q'=\Psi ^+_C$
,
$Q'=\Psi ^+_C$
,
 $s_i(\gamma )$
has type
$s_i(\gamma )$
has type
 $A^{p-1}CN^r$
, and
$A^{p-1}CN^r$
, and
 $Q"=\Psi ^+_N$
;
$Q"=\Psi ^+_N$
; -
(2)
 $Q=\Psi ^+_N$
,
$Q=\Psi ^+_N$
,
 $Q'=\Psi ^+_C$
,
$Q'=\Psi ^+_C$
,
 $s_i(\gamma )$
has type
$s_i(\gamma )$
has type
 $A^pCN^{r-1}$
, and
$A^pCN^{r-1}$
, and
 $Q"=\Psi ^+_A$
.
$Q"=\Psi ^+_A$
.
Let
![]() $\gamma _x=\prod _{\beta \in x}\beta $
for all
$\gamma _x=\prod _{\beta \in x}\beta $
for all
![]() $x\in \{Q,Q',Q"\}$
, and write
$x\in \{Q,Q',Q"\}$
, and write
![]() $\gamma =\gamma _1\gamma _Q$
. Then we have
$\gamma =\gamma _1\gamma _Q$
. Then we have
![]() $\gamma _{Q'}=\gamma _Q+\gamma _{Q"}$
, and thus,
$\gamma _{Q'}=\gamma _Q+\gamma _{Q"}$
, and thus,
in both of the above cases. We have
![]() $\alpha _i\in \Psi $
by Proposition 3.8 (ii), and
$\alpha _i\in \Psi $
by Proposition 3.8 (ii), and
![]() $\alpha _i$
must lie in the induced simple system of
$\alpha _i$
must lie in the induced simple system of
![]() $\Psi $
since it is simple. Theorem 3.10 (v) then implies that
$\Psi $
since it is simple. Theorem 3.10 (v) then implies that
![]() $\alpha \notin Q'$
, and we have
$\alpha \notin Q'$
, and we have
![]() $\alpha _i\notin Q$
by assumption, so we have
$\alpha _i\notin Q$
by assumption, so we have
![]() $\alpha \in Q"$
. It follows that
$\alpha \in Q"$
. It follows that
![]() $\alpha $
divides the n-root
$\alpha $
divides the n-root
![]() $\gamma "=\gamma _1\gamma _{Q"}$
.
$\gamma "=\gamma _1\gamma _{Q"}$
.
It remains to prove that
![]() $\gamma "$
is noncrossing. We treat case (1) first. If
$\gamma "$
is noncrossing. We treat case (1) first. If
![]() $\alpha $
is any root that is minimal in Q, then
$\alpha $
is any root that is minimal in Q, then
![]() $\alpha $
moves the crossing
$\alpha $
moves the crossing
![]() $Q'$
to the nesting
$Q'$
to the nesting
![]() $Q"$
by Theorem 3.10 (vi), so that
$Q"$
by Theorem 3.10 (vi), so that
![]() $\gamma "=s_\alpha (s_i(\gamma ))$
. Since
$\gamma "=s_\alpha (s_i(\gamma ))$
. Since
![]() $s_i(\gamma )$
has type
$s_i(\gamma )$
has type
![]() $A^{p-1}CN^r$
,
$A^{p-1}CN^r$
,
![]() $Q'$
is the unique crossing in
$Q'$
is the unique crossing in
![]() $s_i(\gamma )$
; therefore, any root that moves a C in
$s_i(\gamma )$
; therefore, any root that moves a C in
![]() $s_i(\gamma )$
to an N must move
$s_i(\gamma )$
to an N must move
![]() $Q'$
, and it must move
$Q'$
, and it must move
![]() $Q'$
to
$Q'$
to
![]() $Q"$
by Proposition 3.8 (ii). Together with Theorem 3.10 (vi), this further implies that any root moving
$Q"$
by Proposition 3.8 (ii). Together with Theorem 3.10 (vi), this further implies that any root moving
![]() $Q'$
to
$Q'$
to
![]() $Q"$
must come from Q, so it follows that
$Q"$
must come from Q, so it follows that
![]() $\alpha $
is minimal among roots moving a C in
$\alpha $
is minimal among roots moving a C in
![]() $s_i(\gamma )$
to an N. It follows from Proposition 4.7 (iii) that
$s_i(\gamma )$
to an N. It follows from Proposition 4.7 (iii) that
![]() $\gamma "=s_\alpha (s_i(\gamma ))$
has type
$\gamma "=s_\alpha (s_i(\gamma ))$
has type
![]() $A^{p-1}N^{r+1}$
; therefore,
$A^{p-1}N^{r+1}$
; therefore,
![]() $\gamma "$
is noncrossing. A similar argument shows that
$\gamma "$
is noncrossing. A similar argument shows that
![]() $\gamma "$
has type
$\gamma "$
has type
![]() $A^{p+1}N^{r-1}$
in case (2), so
$A^{p+1}N^{r-1}$
in case (2), so
![]() $\gamma "$
is noncrossing in both cases.
$\gamma "$
is noncrossing in both cases.
Remark 5.8.
-
(i) Since the Weyl group W acts transitively on n-roots in types
 $E_7, E_8$
and
$E_7, E_8$
and
 $D_n$
for n even, the first assertion of Theorem 5.7 (i) is equivalent to the assertion that the noncrossing basis
$D_n$
for n even, the first assertion of Theorem 5.7 (i) is equivalent to the assertion that the noncrossing basis
 $\mathcal B$
is a sign-coherent basis of the Macdonald representation
$\mathcal B$
is a sign-coherent basis of the Macdonald representation
 $j^{\Phi }_{nA_1}({\mathrm {sgn}})$
in the sense of cluster algebras ([Reference Cao and Li10, Definition 2.2 (i)], [25, Definition 6.12]); that is, with respect to
$j^{\Phi }_{nA_1}({\mathrm {sgn}})$
in the sense of cluster algebras ([Reference Cao and Li10, Definition 2.2 (i)], [25, Definition 6.12]); that is, with respect to
 $\mathcal B$
, every element of W acts on
$\mathcal B$
, every element of W acts on
 $j^{\Phi }_{nA_1}({\mathrm {sgn}})$
by a matrix where the entries in each column all have the same sign. It would be interesting to know whether these entries (i.e., the coefficients appearing in the expansion of arbitrary n-roots into the noncrossing elements) have any interpretation in terms of categorification.
$j^{\Phi }_{nA_1}({\mathrm {sgn}})$
by a matrix where the entries in each column all have the same sign. It would be interesting to know whether these entries (i.e., the coefficients appearing in the expansion of arbitrary n-roots into the noncrossing elements) have any interpretation in terms of categorification. -
(ii) There are other constructions of the basis of noncrossing n-roots. For example, one can modify the monomial bases of [Reference Fan23] by specializing the parameter to
 $1$
and twisting by the sign representation, where the monomial basis in turn agrees with a suitable IC basis in the sense of Du [Reference Du21] by a result of the first named author and Losonczy [Reference Green and Losonczy29, Theorem 3.6]. However, the n-root approach has the significant advantage that it is relatively easy, given an arbitrary group element w and an arbitrary n-root
$1$
and twisting by the sign representation, where the monomial basis in turn agrees with a suitable IC basis in the sense of Du [Reference Du21] by a result of the first named author and Losonczy [Reference Green and Losonczy29, Theorem 3.6]. However, the n-root approach has the significant advantage that it is relatively easy, given an arbitrary group element w and an arbitrary n-root
 $\alpha $
, to express
$\alpha $
, to express
 $w(\alpha )$
as a linear combination of basis elements. The bases in type
$w(\alpha )$
as a linear combination of basis elements. The bases in type
 $D_n$
may be constructed diagrammatically in terms of perfect matchings, as we explain at the end of Section 6.1. There is also a diagrammatic construction in types
$D_n$
may be constructed diagrammatically in terms of perfect matchings, as we explain at the end of Section 6.1. There is also a diagrammatic construction in types
 $E_7$
and
$E_7$
and
 $E_8$
, as described in [Reference tom Dieck56] and [Reference Green27], but we do not pursue this here because it is not easy to recover the components of a basis n-root by inspection of the corresponding diagram.
$E_8$
, as described in [Reference tom Dieck56] and [Reference Green27], but we do not pursue this here because it is not easy to recover the components of a basis n-root by inspection of the corresponding diagram. -
(iii) With some more work, it can be shown that every component of a noncrossing n-root has odd height and, conversely, that every root of odd height occurs as a component of some noncrossing n-root.
5.4 Properties of the nonnesting basis
In this subsection, we show that the nonnesting basis is naturally indexed by a distributive lattice whose unique maximal and minimal elements are given by the maximally crossing and aligned n-roots
![]() $\theta _C$
and
$\theta _C$
and
![]() $\theta _A$
, respectively. This lattice is induced by the left weak Bruhat order
$\theta _A$
, respectively. This lattice is induced by the left weak Bruhat order
![]() $\le _L$
of W and is isomorphic to a lattice consisting of certain fully commutative elements. We recall that
$\le _L$
of W and is isomorphic to a lattice consisting of certain fully commutative elements. We recall that
![]() $\le _L$
is defined by the condition that
$\le _L$
is defined by the condition that
![]() $v\le _L w$
if
$v\le _L w$
if
![]() $w=uv$
for some
$w=uv$
for some
![]() $u\in W$
such that
$u\in W$
such that
![]() $\ell (w)=\ell (u)+\ell (v)$
or, equivalently, by the condition that
$\ell (w)=\ell (u)+\ell (v)$
or, equivalently, by the condition that
![]() $\ell (wv^{-1})+\ell (v)=\ell (w)$
. An element w in a simply laced Weyl group is fully commutative precisely when no reduced word for w contains a factor of the form
$\ell (wv^{-1})+\ell (v)=\ell (w)$
. An element w in a simply laced Weyl group is fully commutative precisely when no reduced word for w contains a factor of the form
![]() $s_i s_j s_i$
[Reference Stembridge54].
$s_i s_j s_i$
[Reference Stembridge54].
Definition 5.9. Let
![]() $\theta ,\theta '$
be two nonnesting positive n-roots. A nonnesting sequence from
$\theta ,\theta '$
be two nonnesting positive n-roots. A nonnesting sequence from
![]() $\theta $
to
$\theta $
to
![]() $\theta '$
is a (possibly trivial) sequence
$\theta '$
is a (possibly trivial) sequence
![]() $(\theta _i) = (\theta _0=\theta , \theta _1, \ldots , \theta _r=\theta ')$
of positive nonnesting n-roots such that for all
$(\theta _i) = (\theta _0=\theta , \theta _1, \ldots , \theta _r=\theta ')$
of positive nonnesting n-roots such that for all
![]() $1 \leq j \leq r$
, there exists a simple root
$1 \leq j \leq r$
, there exists a simple root
![]() $\alpha _{i_j}$
such that
$\alpha _{i_j}$
such that
If
![]() $s_{i_1}, s_{i_2}, \cdots , s_{i_r}$
are simple reflections satisfying the condition in (5.1), we say that
$s_{i_1}, s_{i_2}, \cdots , s_{i_r}$
are simple reflections satisfying the condition in (5.1), we say that
![]() ${\mathbf {w} = s_{i_1} s_{i_2} \cdots s_{i_r}}$
is a
${\mathbf {w} = s_{i_1} s_{i_2} \cdots s_{i_r}}$
is a
![]() $(\theta ,\theta ')$
-word, and we call the element w expressed by
$(\theta ,\theta ')$
-word, and we call the element w expressed by
![]() $\mathbf {w}$
a
$\mathbf {w}$
a
![]() $(\theta ,\theta ')$
-element. Note that we have
$(\theta ,\theta ')$
-element. Note that we have
![]() $w(\theta ')=\theta $
.
$w(\theta ')=\theta $
.
Remark 5.10. Let
![]() $\theta $
be a nonnesting positive n-root of type
$\theta $
be a nonnesting positive n-root of type
![]() $A^pC^q$
and let
$A^pC^q$
and let
![]() $\alpha _i$
be a simple root. The condition that
$\alpha _i$
be a simple root. The condition that
![]() $\sigma (s_i(\theta ))>\sigma (\theta )$
is equivalent to the condition that
$\sigma (s_i(\theta ))>\sigma (\theta )$
is equivalent to the condition that
![]() $B(\sigma (\theta ),\alpha _i)<0$
by Equation (2.1) because
$B(\sigma (\theta ),\alpha _i)<0$
by Equation (2.1) because
![]() $\sigma (s_i(\theta ))=s_i(\sigma (\theta ))$
. In addition, by Corollary 4.9 (ii) and (iii), the condition that
$\sigma (s_i(\theta ))=s_i(\sigma (\theta ))$
. In addition, by Corollary 4.9 (ii) and (iii), the condition that
![]() $\sigma (s_i(\theta ))>\sigma (\theta )$
is also equivalent to the condition that
$\sigma (s_i(\theta ))>\sigma (\theta )$
is also equivalent to the condition that
![]() $\sigma (s_i(\theta ))=\sigma (\theta )+2\alpha _i$
, or the condition that
$\sigma (s_i(\theta ))=\sigma (\theta )+2\alpha _i$
, or the condition that
![]() $s_i$
moves
$s_i$
moves
![]() $\theta $
to an n-root of type
$\theta $
to an n-root of type
![]() $A^{p-1}C^{q+1}$
. It follows that if
$A^{p-1}C^{q+1}$
. It follows that if
![]() $(\theta _0,\theta _1,\cdots ,\theta _r)$
is a nonnesting sequence, then we have
$(\theta _0,\theta _1,\cdots ,\theta _r)$
is a nonnesting sequence, then we have
![]() $\lambda (\theta _j)=\lambda (\theta _{j-1})+1$
for all
$\lambda (\theta _j)=\lambda (\theta _{j-1})+1$
for all
![]() $1\le j\le r$
. In particular, every nonnesting sequence is a saturated chain with respect to the quasiparabolic order
$1\le j\le r$
. In particular, every nonnesting sequence is a saturated chain with respect to the quasiparabolic order
![]() $\le _Q$
.
$\le _Q$
.
Remark 5.11. Let
![]() $\theta $
and
$\theta $
and
![]() $\theta '$
be two positive n-roots with
$\theta '$
be two positive n-roots with
![]() $\lambda (\theta ')>\lambda (\theta )$
, and let
$\lambda (\theta ')>\lambda (\theta )$
, and let
![]() $w\in W$
be an element such that
$w\in W$
be an element such that
![]() $w(\theta ')=\theta $
. Let
$w(\theta ')=\theta $
. Let
![]() $\mathbf {w}=s_{i_1}\cdots s_{i_r}$
be an arbitrary word for w. By the definition of quasiparabolic sets, applying a simple reflection decreases the level by at most 1, so any element taking
$\mathbf {w}=s_{i_1}\cdots s_{i_r}$
be an arbitrary word for w. By the definition of quasiparabolic sets, applying a simple reflection decreases the level by at most 1, so any element taking
![]() $\theta '$
to
$\theta '$
to
![]() $\theta $
has length at least
$\theta $
has length at least
![]() $\lambda (\theta ')-\lambda (\theta )$
. It follows that
$\lambda (\theta ')-\lambda (\theta )$
. It follows that
![]() $r\ge \lambda (\theta ')-\lambda (\theta )$
. It also follows that if
$r\ge \lambda (\theta ')-\lambda (\theta )$
. It also follows that if
![]() $r=\lambda (\theta ')-\lambda (\theta )$
, then
$r=\lambda (\theta ')-\lambda (\theta )$
, then
![]() $\mathbf {w}$
is reduced and successively applying the simple reflections
$\mathbf {w}$
is reduced and successively applying the simple reflections
![]() $s_{i_r}, \cdots , s_{i_2}, s_{i_1}$
starting from
$s_{i_r}, \cdots , s_{i_2}, s_{i_1}$
starting from
![]() $\theta '$
must reduce the level by 1 at each step. In particular, if
$\theta '$
must reduce the level by 1 at each step. In particular, if
![]() $r=\lambda (\theta ')-\lambda (\theta )$
and
$r=\lambda (\theta ')-\lambda (\theta )$
and
![]() $\theta '$
is nonnesting, then it follows from Proposition 4.7 (i) that each of these simple reflections is a
$\theta '$
is nonnesting, then it follows from Proposition 4.7 (i) that each of these simple reflections is a
![]() $CA$
move, so that conversely the sequence
$CA$
move, so that conversely the sequence
![]() $\theta _{\mathbf {w}}:=(\theta _0,\cdots , \theta _r)$
defined by
$\theta _{\mathbf {w}}:=(\theta _0,\cdots , \theta _r)$
defined by
![]() $\theta _0=\theta , \theta _j=s_{i_j}(\theta _{j-1})$
for
$\theta _0=\theta , \theta _j=s_{i_j}(\theta _{j-1})$
for
![]() $1\le j\le r$
must be a nonnesting sequence by Remark 5.10.
$1\le j\le r$
must be a nonnesting sequence by Remark 5.10.
Proposition 5.12. Let
![]() $W_I\subset W$
be the parabolic subgroup of Proposition 5.2 (i), and let
$W_I\subset W$
be the parabolic subgroup of Proposition 5.2 (i), and let
![]() $\theta $
be a nonnesting positive n-root of type
$\theta $
be a nonnesting positive n-root of type
![]() $A^pC^q$
.
$A^pC^q$
.
-
(i) If
 $\theta $
is the maximally crossing element
$\theta $
is the maximally crossing element
 $\theta _C$
, then we have
$\theta _C$
, then we have
 $B(\sigma (\theta ), \alpha _i)\ge 0$
for every simple root
$B(\sigma (\theta ), \alpha _i)\ge 0$
for every simple root
 $\alpha _i$
. Otherwise, there exists a simple root
$\alpha _i$
. Otherwise, there exists a simple root
 $\alpha _i$
such that
$\alpha _i$
such that
 $B(\sigma (\theta ), \alpha _i)<0$
.
$B(\sigma (\theta ), \alpha _i)<0$
. -
(ii) There exists a nonnesting sequence from
 $\theta $
to
$\theta $
to
 $\theta _C$
, and we have
$\theta _C$
, and we have
 $\textrm {ht}(\sigma (\theta ))=\textrm {ht}(\sigma (\theta _C))-2p$
.
$\textrm {ht}(\sigma (\theta ))=\textrm {ht}(\sigma (\theta _C))-2p$
. -
(iii) Every
 $(\theta ,\theta _C)$
-word is reduced. Every
$(\theta ,\theta _C)$
-word is reduced. Every
 $(\theta ,\theta _C)$
-element is fully commutative and has length p. Every shortest element taking
$(\theta ,\theta _C)$
-element is fully commutative and has length p. Every shortest element taking
 $\theta _C$
to
$\theta _C$
to
 $\theta $
has length p.
$\theta $
has length p. -
(iv) There is a unique
 $(\theta ,\theta _C)$
-element w. It is the unique shortest element in the coset
$(\theta ,\theta _C)$
-element w. It is the unique shortest element in the coset
 $wW_I$
and is also the unique shortest element in W taking
$wW_I$
and is also the unique shortest element in W taking
 $\theta _C$
to
$\theta _C$
to
 $\theta $
.
$\theta $
. -
(v) There exists a nonnesting sequence from the maximally aligned element
 $\theta _A$
to
$\theta _A$
to
 $\theta _C$
that includes
$\theta _C$
that includes
 $\theta $
.
$\theta $
.
Proof. The first assertion of (i) follows from Proposition 5.1 (iii) and the fact that
![]() $\sigma (\theta _C)=\sigma (\theta _N)$
by Proposition 5.2. Let V be the reflection representation of W and let
$\sigma (\theta _C)=\sigma (\theta _N)$
by Proposition 5.2. Let V be the reflection representation of W and let
The set D is a fundamental domain for the action of W on V by [Reference Humphreys33, Theorem 1.12 (a)], and we have
![]() $\theta _C\in D$
. If
$\theta _C\in D$
. If
![]() $\theta $
is a nonnesting n-root different from
$\theta $
is a nonnesting n-root different from
![]() $\theta _C$
, then
$\theta _C$
, then
![]() $\theta $
and
$\theta $
and
![]() $\theta _C$
are conjugate under the action of W by Lemma 3.2, and therefore so are
$\theta _C$
are conjugate under the action of W by Lemma 3.2, and therefore so are
![]() $\sigma (\theta )$
and
$\sigma (\theta )$
and
![]() $\sigma (\theta _C)$
. It follows that
$\sigma (\theta _C)$
. It follows that
![]() $\theta \not \in D$
; therefore, we have
$\theta \not \in D$
; therefore, we have
![]() $B(\sigma (\theta ),\alpha _i)<0$
for some simple root
$B(\sigma (\theta ),\alpha _i)<0$
for some simple root
![]() $\alpha _i$
.
$\alpha _i$
.
We prove (ii) by induction on p. If
![]() $p=0$
, then
$p=0$
, then
![]() $\theta =\theta _C$
by Proposition 5.2 (iii) and the conclusion of (ii) holds trivially. If
$\theta =\theta _C$
by Proposition 5.2 (iii) and the conclusion of (ii) holds trivially. If
![]() $p>0$
, then
$p>0$
, then
![]() $\theta \neq \theta _C$
and there exists a simple root
$\theta \neq \theta _C$
and there exists a simple root
![]() $\alpha _i$
with
$\alpha _i$
with
![]() $B(\sigma (\theta ),\alpha _i)<0$
by (i). The simple reflection
$B(\sigma (\theta ),\alpha _i)<0$
by (i). The simple reflection
![]() $s_i$
satisfies the condition (5.1), adds 2 to the height of the sum, and sends
$s_i$
satisfies the condition (5.1), adds 2 to the height of the sum, and sends
![]() $\theta $
to an n-root of type
$\theta $
to an n-root of type
![]() $A^{p-1}C^{q+1}$
by Remark 5.10, so (ii) follows by induction.
$A^{p-1}C^{q+1}$
by Remark 5.10, so (ii) follows by induction.
Let
![]() $\mathbf {w}=s_{i_1}\cdots s_{i_r}$
be a
$\mathbf {w}=s_{i_1}\cdots s_{i_r}$
be a
![]() $(\theta ,\theta _C)$
-word expressing a
$(\theta ,\theta _C)$
-word expressing a
![]() $(\theta ,\theta _C)$
element w. Then w takes
$(\theta ,\theta _C)$
element w. Then w takes
![]() $\theta _C$
to
$\theta _C$
to
![]() $\theta $
, and we have
$\theta $
, and we have
![]() $r=\lambda (\theta _C)-\lambda (\theta )=p$
by by Remark 5.10. Remark 5.11 then implies that
$r=\lambda (\theta _C)-\lambda (\theta )=p$
by by Remark 5.10. Remark 5.11 then implies that
![]() $\mathbf {w}$
is reduced. It follows that
$\mathbf {w}$
is reduced. It follows that
![]() $\ell (w)=r=p$
. Since an element taking
$\ell (w)=r=p$
. Since an element taking
![]() $\theta _C$
to
$\theta _C$
to
![]() $\theta $
has length at least
$\theta $
has length at least
![]() $\lambda (\theta _C)-\lambda (\theta )=p$
by Remark 5.11 and w is such a shortest element, it also follows that every shortest element taking
$\lambda (\theta _C)-\lambda (\theta )=p$
by Remark 5.11 and w is such a shortest element, it also follows that every shortest element taking
![]() $\theta _C$
to
$\theta _C$
to
![]() $\theta $
has length p.
$\theta $
has length p.
To prove (iii), it remains to show that
![]() $\mathbf {w}$
cannot contain a factor of the form
$\mathbf {w}$
cannot contain a factor of the form
![]() $s_{\alpha _i} s_{\alpha _j} s_{\alpha _i}$
. By Remark 5.10 and direct computation, such a factor would imply the existence of a subsequence
$s_{\alpha _i} s_{\alpha _j} s_{\alpha _i}$
. By Remark 5.10 and direct computation, such a factor would imply the existence of a subsequence
![]() $(\theta _a, \theta _{a+1}, \theta _{a+2}, \theta _{a+3})$
such that
$(\theta _a, \theta _{a+1}, \theta _{a+2}, \theta _{a+3})$
such that
This contradicts the fact that
![]() $s_{\alpha _i}(\theta _{a+2})=\theta _{a+3}$
, which completes the proof of (iii).
$s_{\alpha _i}(\theta _{a+2})=\theta _{a+3}$
, which completes the proof of (iii).
Let w be a shortest element taking
![]() $\theta _C$
to
$\theta _C$
to
![]() $\theta $
. Then w has length
$\theta $
. Then w has length
![]() $p=\lambda (\theta _C)-\lambda (\theta )$
by (iii). Let
$p=\lambda (\theta _C)-\lambda (\theta )$
by (iii). Let
![]() $\mathbf {w}=s_{i_1}\dots s_{i_p}$
be a reduced word for w. Remark 5.11 implies that if we start from
$\mathbf {w}=s_{i_1}\dots s_{i_p}$
be a reduced word for w. Remark 5.11 implies that if we start from
![]() $\theta _C$
and apply
$\theta _C$
and apply
![]() $s_{i_p}, \cdots , s_{i_2}, s_{i_1}$
successively, each simple reflection must be a
$s_{i_p}, \cdots , s_{i_2}, s_{i_1}$
successively, each simple reflection must be a
![]() $CA$
move. In particular,
$CA$
move. In particular,
![]() $s_{i_p}$
must perform a
$s_{i_p}$
must perform a
![]() $CA$
move on
$CA$
move on
![]() $\theta _C$
, so we have
$\theta _C$
, so we have
by Corollary 4.9 (ii). This implies that
![]() $B(\sigma (\theta _N),\alpha _{i_p})=B(\sigma (\theta _C), \alpha _{i_p})>0$
, so it follows from Proposition 5.1 (iii) that
$B(\sigma (\theta _N),\alpha _{i_p})=B(\sigma (\theta _C), \alpha _{i_p})>0$
, so it follows from Proposition 5.1 (iii) that
![]() $\alpha _{i_p}=\alpha _x$
where
$\alpha _{i_p}=\alpha _x$
where
![]() $\alpha _x$
is the unique Coxeter generator of W not in I. In other words, every reduced word for w ends in
$\alpha _x$
is the unique Coxeter generator of W not in I. In other words, every reduced word for w ends in
![]() $s_{\alpha _x}$
. It follows from [Reference Humphreys33, Proposition 1.10 (c)] that w is the unique shortest element in
$s_{\alpha _x}$
. It follows from [Reference Humphreys33, Proposition 1.10 (c)] that w is the unique shortest element in
![]() $wW_I$
.
$wW_I$
.
If
![]() $w'$
is another shortest element taking
$w'$
is another shortest element taking
![]() $\theta _C$
to
$\theta _C$
to
![]() $\theta $
, then
$\theta $
, then
![]() $w'w^{-1}(\theta _C)=\theta _C$
, so
$w'w^{-1}(\theta _C)=\theta _C$
, so
![]() $w'w^{-1}\in W_I$
by Proposition 5.1 (iv). It follows that the cosets
$w'w^{-1}\in W_I$
by Proposition 5.1 (iv). It follows that the cosets
![]() $wW_I$
and
$wW_I$
and
![]() $w'W_I$
are equal; therefore, we have
$w'W_I$
are equal; therefore, we have
![]() $w=w'$
because w and
$w=w'$
because w and
![]() $w'$
are both the unique shortest element in the common coset
$w'$
are both the unique shortest element in the common coset
![]() $wW_I=w'W_I$
by the last paragraph. This proves the uniqueness of the shortest element taking
$wW_I=w'W_I$
by the last paragraph. This proves the uniqueness of the shortest element taking
![]() $\theta _C$
to
$\theta _C$
to
![]() $\theta $
. Part (iii) says that each
$\theta $
. Part (iii) says that each
![]() $(\theta ,\theta _C)$
-element is such a shortest element, and (iv) now follows.
$(\theta ,\theta _C)$
-element is such a shortest element, and (iv) now follows.
Finally, to prove (v), we recall from Proposition 4.11 (i) that
![]() $\theta _A$
is the unique minimal element of the set X. It follows from [Reference Rains and Vazirani43, Theorem 2.8] that there exists an element
$\theta _A$
is the unique minimal element of the set X. It follows from [Reference Rains and Vazirani43, Theorem 2.8] that there exists an element
![]() $u\in W$
such that
$u\in W$
such that
![]() $u(\theta _A)=\theta $
and
$u(\theta _A)=\theta $
and
![]() $\ell (u)=\lambda (\theta )-\lambda (\theta _A)=q$
. Let v be the unique
$\ell (u)=\lambda (\theta )-\lambda (\theta _A)=q$
. Let v be the unique
![]() $(\theta ,\theta _C)$
-element, let
$(\theta ,\theta _C)$
-element, let
![]() $s_{i_1}\cdots s_{i_p}$
be a reduced word for v, and let
$s_{i_1}\cdots s_{i_p}$
be a reduced word for v, and let
![]() $s^{\prime }_{i_1}\cdots s^{\prime }_{i_q}$
be a reduced word for
$s^{\prime }_{i_1}\cdots s^{\prime }_{i_q}$
be a reduced word for
![]() $u^{-1}$
. Then
$u^{-1}$
. Then
![]() $u^{-1} v$
takes
$u^{-1} v$
takes
![]() $\theta _C$
to
$\theta _C$
to
![]() $\theta _A$
and has length at most
$\theta _A$
and has length at most
![]() $p+q=M=\lambda (\theta _C)-\lambda (\theta _A)$
, so
$p+q=M=\lambda (\theta _C)-\lambda (\theta _A)$
, so
![]() $u^{-1} v$
must be the unique
$u^{-1} v$
must be the unique
![]() $(\theta _A,\theta _C)$
-element by (ii) and (iii), and the word
$(\theta _A,\theta _C)$
-element by (ii) and (iii), and the word
![]() $\mathbf {w}=s^{\prime }_{i_1}\cdots s^{\prime }_{i_q}s_{i_1}\cdots s_{i_p}$
must be a reduced word for
$\mathbf {w}=s^{\prime }_{i_1}\cdots s^{\prime }_{i_q}s_{i_1}\cdots s_{i_p}$
must be a reduced word for
![]() $u^{-1} v$
. Remark 5.11 now implies that starting from
$u^{-1} v$
. Remark 5.11 now implies that starting from
![]() $\theta _A$
and applying
$\theta _A$
and applying
![]() $s^{\prime }_{i_1}, \cdots , s^{\prime }_{i_q}, s_{i_1},\cdots , s_{i_p}$
successively yields a nonnesting sequence
$s^{\prime }_{i_1}, \cdots , s^{\prime }_{i_q}, s_{i_1},\cdots , s_{i_p}$
successively yields a nonnesting sequence
![]() $\theta _{\mathbf {w}}$
from
$\theta _{\mathbf {w}}$
from
![]() $\theta _A$
to
$\theta _A$
to
![]() $\theta _C$
that reaches
$\theta _C$
that reaches
![]() $\theta =v\theta _C$
after the first q steps, and (v) follows.
$\theta =v\theta _C$
after the first q steps, and (v) follows.
Theorem 5.13. Let W be a Weyl group of rank n of types
![]() $E_7$
,
$E_7$
,
![]() $E_8$
or
$E_8$
or
![]() $D_n$
for n even. Let M be the number of coplanar quadruples in a maximal orthogonal set, and let
$D_n$
for n even. Let M be the number of coplanar quadruples in a maximal orthogonal set, and let
![]() $W_I$
be the parabolic subgroup of Proposition 5.2 (i).
$W_I$
be the parabolic subgroup of Proposition 5.2 (i).
-
(i) There is a unique element
 $w_N \in W$
of minimal length such that
$w_N \in W$
of minimal length such that
 $w_N(\theta _C) = \theta _A$
. The element
$w_N(\theta _C) = \theta _A$
. The element
 $w_N$
is fully commutative and has length
$w_N$
is fully commutative and has length
 $\ell (w_N) = M$
, and is the unique element of minimal length in the coset
$\ell (w_N) = M$
, and is the unique element of minimal length in the coset
 $w_N W_I$
.
$w_N W_I$
. -
(ii) The set
is a complete, irredundantly described set of nonnesting positive n-roots. The set L has the structure of a distributive lattice, induced by the weak Bruhat order $$ \begin{align*}L= \{v(\theta_C) : v \leq_L w_N\}\end{align*} $$
$$ \begin{align*}L= \{v(\theta_C) : v \leq_L w_N\}\end{align*} $$
 $\leq _L$
.
$\leq _L$
.
-
(iii) If
 $\gamma _1$
and
$\gamma _1$
and
 $\gamma _2$
are positive n-roots satisfying
$\gamma _2$
are positive n-roots satisfying
 $\textrm {ht}(\sigma (\gamma _1)) - \textrm {ht}(\sigma (\gamma _2)) = 2M$
, and w is an element expressed by a word
$\textrm {ht}(\sigma (\gamma _1)) - \textrm {ht}(\sigma (\gamma _2)) = 2M$
, and w is an element expressed by a word
 $\mathbf {w}$
of length M satisfying
$\mathbf {w}$
of length M satisfying
 $w(\gamma _1) = \pm \gamma _2$
, then
$w(\gamma _1) = \pm \gamma _2$
, then
 $\mathbf {w}$
is reduced, and we must have
$\mathbf {w}$
is reduced, and we must have
 $\gamma _1 = \theta _C$
,
$\gamma _1 = \theta _C$
,
 $\gamma _2 = \theta _A$
,
$\gamma _2 = \theta _A$
,
 $w = w_N$
and
$w = w_N$
and
 $w(\gamma _1) = \gamma _2$
.
$w(\gamma _1) = \gamma _2$
.
Proof. Part (i) follows from Proposition 5.12 in the case where
![]() $\theta _0 = \theta _A$
.
$\theta _0 = \theta _A$
.
Let
![]() $w_N \in W$
be as in (i) and let
$w_N \in W$
be as in (i) and let
![]() $v\le _L w_N$
. We may complete a reduced word
$v\le _L w_N$
. We may complete a reduced word
![]() $\mathbf {v}$
for v to a reduced word of the form
$\mathbf {v}$
for v to a reduced word of the form
![]() $\mathbf {w}=\mathbf {u}\cdot \mathbf {v}$
for
$\mathbf {w}=\mathbf {u}\cdot \mathbf {v}$
for
![]() $w_N$
. Remark 5.11 implies that
$w_N$
. Remark 5.11 implies that
![]() $\mathbf {w}$
gives rise to a nonnesting sequence
$\mathbf {w}$
gives rise to a nonnesting sequence
![]() $\theta _{\mathbf {w}}$
from
$\theta _{\mathbf {w}}$
from
![]() $\theta _A$
to
$\theta _A$
to
![]() $\theta _C$
that passes
$\theta _C$
that passes
![]() $v(w_N)$
. It follows that the elements of L are indeed all nonnesting positive n-roots. Conversely, for every nonnesting positive root
$v(w_N)$
. It follows that the elements of L are indeed all nonnesting positive n-roots. Conversely, for every nonnesting positive root
![]() $\theta $
, it follows from Proposition 5.12 (v) and its proof that
$\theta $
, it follows from Proposition 5.12 (v) and its proof that
![]() $\theta =v(\theta _C)$
for some element
$\theta =v(\theta _C)$
for some element
![]() $v\le _L w_N$
, so the list L is complete. Finally, if
$v\le _L w_N$
, so the list L is complete. Finally, if
![]() $v\le _L w_N$
and
$v\le _L w_N$
and
![]() $v'\le _L w_N$
are elements such that
$v'\le _L w_N$
are elements such that
![]() $v(\theta _C)=v'(\theta _C)$
, then
$v(\theta _C)=v'(\theta _C)$
, then
![]() $v'v^{-1}$
stabilizes
$v'v^{-1}$
stabilizes
![]() $\theta _C$
and hence
$\theta _C$
and hence
![]() $\sigma (\theta _C)$
, so we have
$\sigma (\theta _C)$
, so we have
![]() $v'v\in W_I$
and
$v'v\in W_I$
and
![]() $v'W_I=vW_I$
. Since
$v'W_I=vW_I$
. Since
![]() $w_N$
is the shortest element in
$w_N$
is the shortest element in
![]() $w_NW_I$
, the elements
$w_NW_I$
, the elements
![]() $v'$
and v must be the shortest elements in
$v'$
and v must be the shortest elements in
![]() $vW_I$
and
$vW_I$
and
![]() $v'W_I$
as well, which implies that
$v'W_I$
as well, which implies that
![]() $v=v'$
as well. It follows that the list L irredundantly describes the positive nonnesting n-roots, proving the first statement of (ii).
$v=v'$
as well. It follows that the list L irredundantly describes the positive nonnesting n-roots, proving the first statement of (ii).
By [Reference Stembridge54, Theorem 3.2], the fact that
![]() $w_N$
is fully commutative implies that the poset
$w_N$
is fully commutative implies that the poset
![]() $\{x : x \leq _L w\}$
is a distributive lattice. This completes the proof of (ii).
$\{x : x \leq _L w\}$
is a distributive lattice. This completes the proof of (ii).
Suppose that the conditions of (iii) hold, and let
![]() $s_{i_1} s_{i_2} \cdots s_{i_M}$
be a reduced expression for w. Since
$s_{i_1} s_{i_2} \cdots s_{i_M}$
be a reduced expression for w. Since
![]() $\textrm {ht}(\sigma (\gamma _1))-\textrm {ht}(\sigma (\gamma _2))=2M$
, as we start from
$\textrm {ht}(\sigma (\gamma _1))-\textrm {ht}(\sigma (\gamma _2))=2M$
, as we start from
![]() $\theta _C$
and successively apply the simple reflection
$\theta _C$
and successively apply the simple reflection
![]() $s_{i_M}, \dots , s_{i_2}, s_{i_1}$
, the application of each simple reflection
$s_{i_M}, \dots , s_{i_2}, s_{i_1}$
, the application of each simple reflection
![]() $s_{i_j}$
must subtract
$s_{i_j}$
must subtract
![]() $2$
from the height of the sum and change a C to an A by Corollary 4.9 (ii). It is therefore not possible at any stage for a simple reflection to negate a component of an n-root, which implies that we have
$2$
from the height of the sum and change a C to an A by Corollary 4.9 (ii). It is therefore not possible at any stage for a simple reflection to negate a component of an n-root, which implies that we have
![]() $w(\gamma _1)=\gamma _2$
. Each simple reflection
$w(\gamma _1)=\gamma _2$
. Each simple reflection
![]() $s_{i_j}$
also causes no change in the number of nestings by Proposition 4.7 (i), so the fact that
$s_{i_j}$
also causes no change in the number of nestings by Proposition 4.7 (i), so the fact that
![]() $\textrm {ht}(\sigma (\gamma _1))-\textrm {ht}(\sigma (\gamma _2))=2M$
implies that
$\textrm {ht}(\sigma (\gamma _1))-\textrm {ht}(\sigma (\gamma _2))=2M$
implies that
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma _2$
have types
$\gamma _2$
have types
![]() $C^M$
and
$C^M$
and
![]() $A^M$
, respectively, so we have
$A^M$
, respectively, so we have
![]() $\gamma _1 = \theta _C$
and
$\gamma _1 = \theta _C$
and
![]() $\gamma _2 = \theta _A$
. We then have
$\gamma _2 = \theta _A$
. We then have
![]() $w = w_N$
by (i), which completes the proof of (iii).
$w = w_N$
by (i), which completes the proof of (iii).
Definition 5.14. We call the element
![]() $w_N$
from Theorem 5.13 (i.e., the unique element of minimal length that sends
$w_N$
from Theorem 5.13 (i.e., the unique element of minimal length that sends
![]() $\theta _C$
to
$\theta _C$
to
![]() $\theta _A$
) the nonnesting element of W.
$\theta _A$
) the nonnesting element of W.
In Section 6, we will compute the nonnesting element explicitly with the help of Theorem 5.13 (iii).
5.5 Sum equivalence
We say that two positive n-roots
![]() $\beta $
and
$\beta $
and
![]() $\gamma $
of W are sum equivalent, or
$\gamma $
of W are sum equivalent, or
![]() $\sigma $
-equivalent, if
$\sigma $
-equivalent, if
![]() $\sigma (\beta ) = \sigma (\gamma )$
. If C and
$\sigma (\beta ) = \sigma (\gamma )$
. If C and
![]() $C'$
are two
$C'$
are two
![]() $\sigma $
-equivalence classes, then we write
$\sigma $
-equivalence classes, then we write
![]() $C\le _\sigma C'$
if
$C\le _\sigma C'$
if
![]() $\sigma (\beta )\le \sigma (\gamma )$
for any
$\sigma (\beta )\le \sigma (\gamma )$
for any
![]() $\beta \in C$
and
$\beta \in C$
and
![]() $\gamma \in C'$
in the usual order
$\gamma \in C'$
in the usual order
![]() $\le $
on roots (Section 2.2). The goal of this subsection is to show that the
$\le $
on roots (Section 2.2). The goal of this subsection is to show that the
![]() $\sigma $
-equivalence classes of X are highly compatible with the quasiparabolic order
$\sigma $
-equivalence classes of X are highly compatible with the quasiparabolic order
![]() $\le _Q$
and the feature-avoiding n-roots.
$\le _Q$
and the feature-avoiding n-roots.
Proposition 5.15. Let
![]() $\mathcal B$
be the set of nonnesting positive n-roots of W.
$\mathcal B$
be the set of nonnesting positive n-roots of W.
-
(i) If
 $\beta , \beta '\in \mathcal B$
are nonnesting positive n-roots with
$\beta , \beta '\in \mathcal B$
are nonnesting positive n-roots with
 $\sigma (\beta ) = \sigma (\beta ')$
, then we have
$\sigma (\beta ) = \sigma (\beta ')$
, then we have
 $\beta = \beta '$
.
$\beta = \beta '$
. -
(ii) Each positive n-root
 $\gamma $
is
$\gamma $
is
 $\sigma $
-equivalent to a unique nonnesting n-root
$\sigma $
-equivalent to a unique nonnesting n-root
 $f(\gamma )$
and a unique noncrossing n-root
$f(\gamma )$
and a unique noncrossing n-root
 $g(\gamma )$
. We have
$g(\gamma )$
. We have
 $f(\gamma )\le _Q \gamma $
, and for suitable integers
$f(\gamma )\le _Q \gamma $
, and for suitable integers $$ \begin{align*} \gamma=f(\gamma)+\sum_{\beta\in \mathcal B: \sigma(\beta)<\sigma(\gamma)} \lambda_{\beta,\gamma}\beta \end{align*} $$
$$ \begin{align*} \gamma=f(\gamma)+\sum_{\beta\in \mathcal B: \sigma(\beta)<\sigma(\gamma)} \lambda_{\beta,\gamma}\beta \end{align*} $$
 $\lambda _{\beta ,\gamma }$
.
$\lambda _{\beta ,\gamma }$
.
-
(iii) Every
 $\sigma $
-equivalence class contains a unique nonnesting n-root,
$\sigma $
-equivalence class contains a unique nonnesting n-root,
 $\beta _1$
, and a unique noncrossing n-root,
$\beta _1$
, and a unique noncrossing n-root,
 $\beta _2$
. The
$\beta _2$
. The
 $\sigma $
-equivalence class containing
$\sigma $
-equivalence class containing
 $\beta _1$
and
$\beta _1$
and
 $\beta _2$
is equal to the interval in the quasiparabolic set X.
$\beta _2$
is equal to the interval in the quasiparabolic set X. $$ \begin{align*}[\beta_1, \beta_2]_{Q} = \{ \gamma \in X : \beta_1 \leq_Q \gamma \leq_Q \beta_2 \}\end{align*} $$
$$ \begin{align*}[\beta_1, \beta_2]_{Q} = \{ \gamma \in X : \beta_1 \leq_Q \gamma \leq_Q \beta_2 \}\end{align*} $$
-
(iv) The set of alignment-free positive n-roots is a
 $\sigma $
-equivalence class and is equal to the interval
$\sigma $
-equivalence class and is equal to the interval
 $[\theta _C,\theta _N]_Q$
in the quasiparabolic set X. It is the unique maximal
$[\theta _C,\theta _N]_Q$
in the quasiparabolic set X. It is the unique maximal
 $\sigma $
-equivalence class with respect to the partial order
$\sigma $
-equivalence class with respect to the partial order
 $\le _\sigma $
.
$\le _\sigma $
.
Proof. Suppose that
![]() $\beta $
and
$\beta $
and
![]() $\beta '$
are nonnesting positive n-roots with
$\beta '$
are nonnesting positive n-roots with
![]() $\sigma (\beta ') = \sigma (\beta )$
. It follows from Proposition 5.12 (ii) that
$\sigma (\beta ') = \sigma (\beta )$
. It follows from Proposition 5.12 (ii) that
![]() $\beta $
and
$\beta $
and
![]() $\beta '$
have the same number of alignments – namely, the number
$\beta '$
have the same number of alignments – namely, the number
![]() $p=(\textrm {ht}(\sigma (\theta _C))-\textrm {ht}(\sigma (\beta )))/2$
. If
$p=(\textrm {ht}(\sigma (\theta _C))-\textrm {ht}(\sigma (\beta )))/2$
. If
![]() $p=0$
, then we have
$p=0$
, then we have
![]() $\beta =\theta _C=\beta '$
by Proposition 5.2 (iii). If
$\beta =\theta _C=\beta '$
by Proposition 5.2 (iii). If
![]() $p>0$
, then neither
$p>0$
, then neither
![]() $\beta $
nor
$\beta $
nor
![]() $\beta '$
equals
$\beta '$
equals
![]() $\theta _C$
, so there is a simple root
$\theta _C$
, so there is a simple root
![]() $\alpha _i$
satisfying
$\alpha _i$
satisfying
![]() $B(\sigma (\beta ),\alpha _i)=B(\sigma (\beta '),\alpha _i)<0$
by Proposition 5.12 (i). By Remark 5.10, both
$B(\sigma (\beta ),\alpha _i)=B(\sigma (\beta '),\alpha _i)<0$
by Proposition 5.12 (i). By Remark 5.10, both
![]() $s_i(\beta )$
and
$s_i(\beta )$
and
![]() $s_i(\beta ')$
are nonnesting positive n-roots with
$s_i(\beta ')$
are nonnesting positive n-roots with
![]() $p-1$
alignments, and we have
$p-1$
alignments, and we have
so (i) follows by induction on p.
Let
![]() $\gamma $
be a positive n-root, and let
$\gamma $
be a positive n-root, and let
![]() $\le _N$
be the nesting order defined in Section 5.2. If
$\le _N$
be the nesting order defined in Section 5.2. If
![]() $\gamma $
contains no nesting, we can simply take
$\gamma $
contains no nesting, we can simply take
![]() $f(\gamma )=\gamma $
. Otherwise, we can factorize
$f(\gamma )=\gamma $
. Otherwise, we can factorize
![]() $\gamma =\gamma '\gamma _N$
where
$\gamma =\gamma '\gamma _N$
where
![]() $\gamma _N$
is a nesting. By the second paragraph of Section 5.2, we can write
$\gamma _N$
is a nesting. By the second paragraph of Section 5.2, we can write
![]() $\gamma =\gamma '\gamma _C-\gamma '\gamma _A$
where we have (a)
$\gamma =\gamma '\gamma _C-\gamma '\gamma _A$
where we have (a)
![]() $\gamma '\gamma _C\le _N\gamma $
, because
$\gamma '\gamma _C\le _N\gamma $
, because
![]() $\sigma (\gamma '\gamma _C)=\sigma (\gamma )$
and
$\sigma (\gamma '\gamma _C)=\sigma (\gamma )$
and
![]() $ \gamma '\gamma _C<_Q \gamma $
, and (b)
$ \gamma '\gamma _C<_Q \gamma $
, and (b)
![]() $\gamma '\gamma _A\le _N\gamma $
, because
$\gamma '\gamma _A\le _N\gamma $
, because
![]() $\sigma (\gamma '\gamma _A)<\sigma (\gamma )$
. Taking
$\sigma (\gamma '\gamma _A)<\sigma (\gamma )$
. Taking
![]() $f(\gamma )=f(\gamma '\gamma _C)$
proves the existence of
$f(\gamma )=f(\gamma '\gamma _C)$
proves the existence of
![]() $f(\gamma )$
and the required expression for
$f(\gamma )$
and the required expression for
![]() $\gamma $
by induction on the order
$\gamma $
by induction on the order
![]() $\le _N$
. The uniqueness of
$\le _N$
. The uniqueness of
![]() $f(\gamma )$
follows from (i). We can use a similar induction using the crossing order
$f(\gamma )$
follows from (i). We can use a similar induction using the crossing order
![]() $\le _C$
to show that
$\le _C$
to show that
![]() $\gamma $
is
$\gamma $
is
![]() $\sigma $
-equivalent to a noncrossing n-root
$\sigma $
-equivalent to a noncrossing n-root
![]() $g(\gamma )$
such that
$g(\gamma )$
such that
![]() $\gamma \leq _Q g(\gamma )$
, and this completes the proof of (ii).
$\gamma \leq _Q g(\gamma )$
, and this completes the proof of (ii).
It follows from (ii) that every
![]() $\sigma $
-equivalence class contains a unique nonnesting n-root, and that the number of
$\sigma $
-equivalence class contains a unique nonnesting n-root, and that the number of
![]() $\sigma $
-equivalence classes equals the number of nonnesting n-roots. The latter number is the dimension of the Macdonald representation and also the number of noncrossing roots by Theorem 5.5 (i) and (ii). Since each
$\sigma $
-equivalence classes equals the number of nonnesting n-roots. The latter number is the dimension of the Macdonald representation and also the number of noncrossing roots by Theorem 5.5 (i) and (ii). Since each
![]() $\sigma $
-equivalence class contains at least one noncrossing n-root by (ii), it follows that each
$\sigma $
-equivalence class contains at least one noncrossing n-root by (ii), it follows that each
![]() $\sigma $
-equivalence class must contain exactly one nonnesting element and exactly one noncrossing element. This proves the first sentence of (iii).
$\sigma $
-equivalence class must contain exactly one nonnesting element and exactly one noncrossing element. This proves the first sentence of (iii).
Let E be a
![]() $\sigma $
-equivalence class with unique nonnesting element
$\sigma $
-equivalence class with unique nonnesting element
![]() $\beta _1$
and unique noncrossing element
$\beta _1$
and unique noncrossing element
![]() $\beta _2$
. Then we have
$\beta _2$
. Then we have
![]() $[\beta _1,\beta _2]_Q\subseteq E$
by Corollary 4.9 (i). Conversely, if
$[\beta _1,\beta _2]_Q\subseteq E$
by Corollary 4.9 (i). Conversely, if
![]() $\gamma $
is an n-root in E, then (ii) and its proof imply that we may find a nonnesting n-root
$\gamma $
is an n-root in E, then (ii) and its proof imply that we may find a nonnesting n-root
![]() $f(\gamma )\in E$
and a noncrossing n-root
$f(\gamma )\in E$
and a noncrossing n-root
![]() $g(\gamma )\in E$
such that
$g(\gamma )\in E$
such that
![]() $f(\gamma )\le _Q \gamma \le _Q g(\gamma )$
. We must have
$f(\gamma )\le _Q \gamma \le _Q g(\gamma )$
. We must have
![]() $f(\gamma )=\beta _1$
and
$f(\gamma )=\beta _1$
and
![]() $g(\gamma _2)=\beta _2$
by the uniqueness of the nonnesting and noncrossing elements in E; therefore, we have
$g(\gamma _2)=\beta _2$
by the uniqueness of the nonnesting and noncrossing elements in E; therefore, we have
![]() $\gamma \in [\beta _1,\beta _2]_Q$
. It follows that
$\gamma \in [\beta _1,\beta _2]_Q$
. It follows that
![]() $E=[\beta _1,\beta _2]_Q$
.
$E=[\beta _1,\beta _2]_Q$
.
For every nonnesting root
![]() $\beta $
not equal to
$\beta $
not equal to
![]() $\theta _C$
, there is a nontrivial nonnesting sequence from
$\theta _C$
, there is a nontrivial nonnesting sequence from
![]() $\beta $
to
$\beta $
to
![]() $\theta _C$
by by Proposition 5.12 (ii), so
$\theta _C$
by by Proposition 5.12 (ii), so
![]() $\sigma (\beta )<\sigma (\theta _C)$
by Definition 5.9. Part (iv) now follows from (iii) and Proposition 5.2 (ii)–(iii).
$\sigma (\beta )<\sigma (\theta _C)$
by Definition 5.9. Part (iv) now follows from (iii) and Proposition 5.2 (ii)–(iii).
Theorem 5.16. Let W be a Weyl group of type
![]() $E_7$
,
$E_7$
,
![]() $E_8$
or
$E_8$
or
![]() $D_n$
for n even. If
$D_n$
for n even. If
![]() $\mathcal B$
is any set of
$\mathcal B$
is any set of
![]() $\sigma $
-equivalence class representatives, then
$\sigma $
-equivalence class representatives, then
![]() $\mathcal B$
is a basis for the Macdonald representation
$\mathcal B$
is a basis for the Macdonald representation
![]() $j^{\Phi }_{nA_1}({\mathrm {sgn}})$
. Furthermore, if we order each such basis
$j^{\Phi }_{nA_1}({\mathrm {sgn}})$
. Furthermore, if we order each such basis
![]() $\mathcal B=\{\beta _1,\cdots ,\beta _k\}$
in a way compatible with the order
$\mathcal B=\{\beta _1,\cdots ,\beta _k\}$
in a way compatible with the order
![]() $\le _\sigma $
(i.e., in such a way that
$\le _\sigma $
(i.e., in such a way that
![]() $i<j$
whenever
$i<j$
whenever
![]() $\beta _i<_\sigma \beta _j$
), then the change of basis matrix between any two such bases is unitriangular with integer entries. In particular, this is true for the change of basis matrix between the nonnesting basis and the noncrossing basis.
$\beta _i<_\sigma \beta _j$
), then the change of basis matrix between any two such bases is unitriangular with integer entries. In particular, this is true for the change of basis matrix between the nonnesting basis and the noncrossing basis.
Proof. By Proposition 5.15 (ii), each element
![]() $\gamma \in \mathcal B$
is the sum of the nonnesting element
$\gamma \in \mathcal B$
is the sum of the nonnesting element
![]() $\gamma '$
that is
$\gamma '$
that is
![]() $\sigma $
-equivalent to
$\sigma $
-equivalent to
![]() $\gamma $
and a
$\gamma $
and a
![]() ${\mathbb Z}$
-linear combination of nonnesting elements with strictly lower sums. The nonnesting elements form a basis for
${\mathbb Z}$
-linear combination of nonnesting elements with strictly lower sums. The nonnesting elements form a basis for
![]() $j^{\Phi }_{nA_1}({\mathrm {sgn}})$
by Theorem 5.5 (i), from which it follows that the set
$j^{\Phi }_{nA_1}({\mathrm {sgn}})$
by Theorem 5.5 (i), from which it follows that the set
![]() $\mathcal B$
is also a basis, and that the change of basis from
$\mathcal B$
is also a basis, and that the change of basis from
![]() $\mathcal B$
to the nonnesting basis is unitriangular with integer entries. If
$\mathcal B$
to the nonnesting basis is unitriangular with integer entries. If
![]() $\mathcal B_1$
and
$\mathcal B_1$
and
![]() $\mathcal B_2$
are two such bases, then the change of basis matrix from
$\mathcal B_2$
are two such bases, then the change of basis matrix from
![]() $\mathcal B_1$
to
$\mathcal B_1$
to
![]() $\mathcal B_2$
is unitriangular with integer entries because it is the product of the matrix changing
$\mathcal B_2$
is unitriangular with integer entries because it is the product of the matrix changing
![]() $\mathcal B_1$
to
$\mathcal B_1$
to
![]() $\mathcal B'$
with the inverse of the matrix changing
$\mathcal B'$
with the inverse of the matrix changing
![]() $\mathcal B_2$
to
$\mathcal B_2$
to
![]() $\mathcal B'$
, both of which are unitriangular with integer entries. Finally, the last assertion follows because Proposition 5.15 (iii) implies that both the nonnesting and noncrossing bases are sets of
$\mathcal B'$
, both of which are unitriangular with integer entries. Finally, the last assertion follows because Proposition 5.15 (iii) implies that both the nonnesting and noncrossing bases are sets of
![]() $\sigma $
-equivalence class representatives.
$\sigma $
-equivalence class representatives.
Remark 5.17. Recall that the Möbius function,
![]() $\mu $
, of a partially ordered set P is defined to satisfy
$\mu $
, of a partially ordered set P is defined to satisfy
![]() $\mu (x, x)=1$
,
$\mu (x, x)=1$
,
![]() $\mu (x, y)=0$
if
$\mu (x, y)=0$
if
![]() $x \not \leq y$
, and
$x \not \leq y$
, and
if
![]() $x < y$
. A poset is Eulerian if we have
$x < y$
. A poset is Eulerian if we have
![]() $\mu (x, y) = (-1)^{\lambda (y) - \lambda (x)}$
whenever
$\mu (x, y) = (-1)^{\lambda (y) - \lambda (x)}$
whenever
![]() $x \leq y$
. It can be shown that if
$x \leq y$
. It can be shown that if
![]() $x, y \in X$
correspond to a nonnesting and noncrossing element, respectively, then the interval
$x, y \in X$
correspond to a nonnesting and noncrossing element, respectively, then the interval
![]() $I = [x, y]$
corresponds to a
$I = [x, y]$
corresponds to a
![]() $\sigma $
-equivalence class if and only if I is Eulerian.
$\sigma $
-equivalence class if and only if I is Eulerian.
Remark 5.18. Reading [Reference Reading44] defines a poset congruence to be an equivalence relation on a poset X such that
-
(i) each equivalence class is an interval;
-
(ii) the projection mapping
 $x \in X$
to the maximal element in its equivalence class is order preserving; and
$x \in X$
to the maximal element in its equivalence class is order preserving; and -
(iii) the projection mapping
 $x \in X$
to the minimal element in its equivalence class is order preserving.
$x \in X$
to the minimal element in its equivalence class is order preserving.
It can be shown using [Reference Watson58, Proposition 42] that, in type
![]() $D_n$
, the equivalence relation induced on X by
$D_n$
, the equivalence relation induced on X by
![]() $\sigma $
is a poset congruence. It can also be shown (by direct computational verification, for example) that the same is true in types
$\sigma $
is a poset congruence. It can also be shown (by direct computational verification, for example) that the same is true in types
![]() $E_7$
and
$E_7$
and
![]() $E_8$
.
$E_8$
.
6 Examples
In this section, we give type-specific details about the n-roots in types
![]() $D_n$
for n even,
$D_n$
for n even,
![]() $E_7$
, and
$E_7$
, and
![]() $E_8$
. In all types, we explicitly describe the maximally aligned, crossing and nesting n-roots
$E_8$
. In all types, we explicitly describe the maximally aligned, crossing and nesting n-roots
![]() $\theta _A, \theta _C$
and
$\theta _A, \theta _C$
and
![]() $\theta _N$
. We find the nonnesting element
$\theta _N$
. We find the nonnesting element
![]() $w_N$
(Definition 5.14), and we use
$w_N$
(Definition 5.14), and we use
![]() $w_N$
and Theorem 5.13 (ii) to deduce the dimension of the Macdonald representation
$w_N$
and Theorem 5.13 (ii) to deduce the dimension of the Macdonald representation
![]() $j^{\Phi }_{nA_1}({\mathrm {sgn}})$
. We also discuss type-specific properties of the set
$j^{\Phi }_{nA_1}({\mathrm {sgn}})$
. We also discuss type-specific properties of the set
![]() $X_I$
of alignment-free positive n-roots for all types. In addition, we explain precise connections between the Macdonald representation
$X_I$
of alignment-free positive n-roots for all types. In addition, we explain precise connections between the Macdonald representation
![]() $j^{\Phi }_{nA_1}({\mathrm {sgn}})$
of type
$j^{\Phi }_{nA_1}({\mathrm {sgn}})$
of type
![]() $D_{2k}$
and a Specht module of the symmetric group
$D_{2k}$
and a Specht module of the symmetric group
![]() $S_{2k}$
(Proposition 6.2),
$S_{2k}$
(Proposition 6.2),
We note that by Lemma 3.1 and Remark 3.11, the noncrossing and nonnesting positive n-roots of type
![]() $D_{2k}$
can be easily recovered from the well-studied noncrossing and nonnesting perfect matchings of
$D_{2k}$
can be easily recovered from the well-studied noncrossing and nonnesting perfect matchings of
![]() $[2k]$
. More generally, in all types, the nonnesting positive n-roots can be computed efficiently via the elements the elements
$[2k]$
. More generally, in all types, the nonnesting positive n-roots can be computed efficiently via the elements the elements
![]() $\theta _C$
and
$\theta _C$
and
![]() $w_N$
by Theorem 5.13 (ii), and it is possible to construct the noncrossing n-roots using Fan’s construction of monomial cells in [Reference Fan23]. In the notation of [Reference Fan23], the maximally aligned n-root
$w_N$
by Theorem 5.13 (ii), and it is possible to construct the noncrossing n-roots using Fan’s construction of monomial cells in [Reference Fan23]. In the notation of [Reference Fan23], the maximally aligned n-root
![]() $\theta _A$
can be identified with the element
$\theta _A$
can be identified with the element
![]() $b_1 b_3 \cdots b_{2k-1}$
in type
$b_1 b_3 \cdots b_{2k-1}$
in type
![]() $D_{2k}$
, with
$D_{2k}$
, with
![]() $b_2 b_4 b_6 b_7$
in type
$b_2 b_4 b_6 b_7$
in type
![]() $E_7$
(with the labelling of Figure 1 (d)), and with
$E_7$
(with the labelling of Figure 1 (d)), and with
![]() $b_2 b_3 b_5 b_7$
in type
$b_2 b_3 b_5 b_7$
in type
![]() $E_8$
(with the labelling of Figure 1 (e)). In types
$E_8$
(with the labelling of Figure 1 (e)). In types
![]() $E_7$
and
$E_7$
and
![]() $E_8$
, it is also possible to use a computer program to find all noncrossing and nonnesting n-roots by generating all the (finitely many) positive n-roots and then removing all n-roots where a crossing or nesting can be found. For these reasons, and to save space, we have chosen not to list the noncrossing and nonnesting bases in type
$E_8$
, it is also possible to use a computer program to find all noncrossing and nonnesting n-roots by generating all the (finitely many) positive n-roots and then removing all n-roots where a crossing or nesting can be found. For these reasons, and to save space, we have chosen not to list the noncrossing and nonnesting bases in type
![]() $E_7$
or
$E_7$
or
![]() $E_8$
in this paper (although the complete lists are available upon request).
$E_8$
in this paper (although the complete lists are available upon request).
6.1 Type
 $D_{2k}$
$D_{2k}$
If W has type
![]() $D_n$
for an even integer
$D_n$
for an even integer
![]() $n=2k$
, then the positive n-roots can be naturally identified with the perfect matchings of
$n=2k$
, then the positive n-roots can be naturally identified with the perfect matchings of
![]() $[n]$
, as explained in Lemma 3.1 (ii). Under this identification, the actions of W on the n-roots and on the matching agree, and the alignments, crossings and nestings in the n-roots correspond to the alignments, crossings and nestings in the matchings in the obvious way by Remark 3.11. We also recall from Section 2.3 and Remark 3.7 that the reflection
$[n]$
, as explained in Lemma 3.1 (ii). Under this identification, the actions of W on the n-roots and on the matching agree, and the alignments, crossings and nestings in the n-roots correspond to the alignments, crossings and nestings in the matchings in the obvious way by Remark 3.11. We also recall from Section 2.3 and Remark 3.7 that the reflection
![]() $r=s_\alpha \in W$
acts as the transposition
$r=s_\alpha \in W$
acts as the transposition
![]() $(ij)$
on the n-roots for each root
$(ij)$
on the n-roots for each root
![]() $\alpha =\varepsilon _i\pm \varepsilon _j$
of W, so that the action of W factors through the homomorphism
$\alpha =\varepsilon _i\pm \varepsilon _j$
of W, so that the action of W factors through the homomorphism
![]() $\phi : W\rightarrow S_{2k}$
of Equation (2.2) to induce an action of
$\phi : W\rightarrow S_{2k}$
of Equation (2.2) to induce an action of
![]() $S_{2k}=W(A_{2k-1})$
on the n-roots, giving the Macdonald representation
$S_{2k}=W(A_{2k-1})$
on the n-roots, giving the Macdonald representation
![]() $j^{\Phi }_{nA_1}({\mathrm {sgn}})$
the structure of an
$j^{\Phi }_{nA_1}({\mathrm {sgn}})$
the structure of an
![]() $S_{2k}$
-module (where the elements of
$S_{2k}$
-module (where the elements of
![]() $S_{2k}$
permute the indices of the terms
$S_{2k}$
permute the indices of the terms
![]() $\varepsilon _i^2$
). The above facts will allow us to connect the theory of n-roots in type
$\varepsilon _i^2$
). The above facts will allow us to connect the theory of n-roots in type
![]() $D_n$
to some widely studied type-A objects and results.
$D_n$
to some widely studied type-A objects and results.
Recall that the number of coplanar quadruples in each positive n-root is
![]() $M=\binom {k}{2}$
, the number of pairs of 2-blocks, by Corollary 3.19.
$M=\binom {k}{2}$
, the number of pairs of 2-blocks, by Corollary 3.19.
Let
![]() $\nu _A, \nu _C $
and
$\nu _A, \nu _C $
and
![]() $\nu _N$
be the positive n-roots corresponding to the matchings
$\nu _N$
be the positive n-roots corresponding to the matchings
![]() $\{12,34,\cdots , (n-1)n\}, \{1(k+1), 2(k+2), \cdots , k(2k)\}$
and
$\{12,34,\cdots , (n-1)n\}, \{1(k+1), 2(k+2), \cdots , k(2k)\}$
and
![]() $\{1n, 2(n-1), \cdots , k(k+1)\}$
, respectively. Every pair of 2-blocks in the first matching forms an alignment, so the matching contains
$\{1n, 2(n-1), \cdots , k(k+1)\}$
, respectively. Every pair of 2-blocks in the first matching forms an alignment, so the matching contains
![]() $\binom {k}{2}=M$
alignments. It then follows from Proposition 4.11 (i) that
$\binom {k}{2}=M$
alignments. It then follows from Proposition 4.11 (i) that
![]() $\nu _A$
is the unique maximally aligned n-root
$\nu _A$
is the unique maximally aligned n-root
![]() $\theta _A$
in the set X. Similar arguments show that
$\theta _A$
in the set X. Similar arguments show that
![]() $\nu _C=\theta _C$
and
$\nu _C=\theta _C$
and
![]() $\nu _N=\theta _N$
by Proposition 5.2 (iii) and Proposition 4.11 (ii), respectively. Note that we have
$\nu _N=\theta _N$
by Proposition 5.2 (iii) and Proposition 4.11 (ii), respectively. Note that we have
![]() $\sigma (\theta _N)=2\sum _{i = 1}^k \varepsilon _i$
.
$\sigma (\theta _N)=2\sum _{i = 1}^k \varepsilon _i$
.
Let w be the element expressed by the word
where
![]() $\mathbf {w}_{i, j} := s_i s_{i+2} s_{i+4} \cdots s_{i+2j}$
. For example, in type
$\mathbf {w}_{i, j} := s_i s_{i+2} s_{i+4} \cdots s_{i+2j}$
. For example, in type
![]() $D_8$
, we have
$D_8$
, we have
![]() $w = (s_2 s_4 s_6)(s_3 s_5)(s_4)$
, and the heap of w is shown in Figure 2 (a). The word
$w = (s_2 s_4 s_6)(s_3 s_5)(s_4)$
, and the heap of w is shown in Figure 2 (a). The word
![]() $\mathbf {w}$
has M letters, and it is straightforward to verify that
$\mathbf {w}$
has M letters, and it is straightforward to verify that
![]() $w(\theta _C)=\theta _A$
, so it follows from Theorem 5.13 (i) that w is the fully commutative nonnesting element
$w(\theta _C)=\theta _A$
, so it follows from Theorem 5.13 (i) that w is the fully commutative nonnesting element
![]() $w_N$
and
$w_N$
and
![]() $\mathbf {w}$
is a reduced word for it.
$\mathbf {w}$
is a reduced word for it.
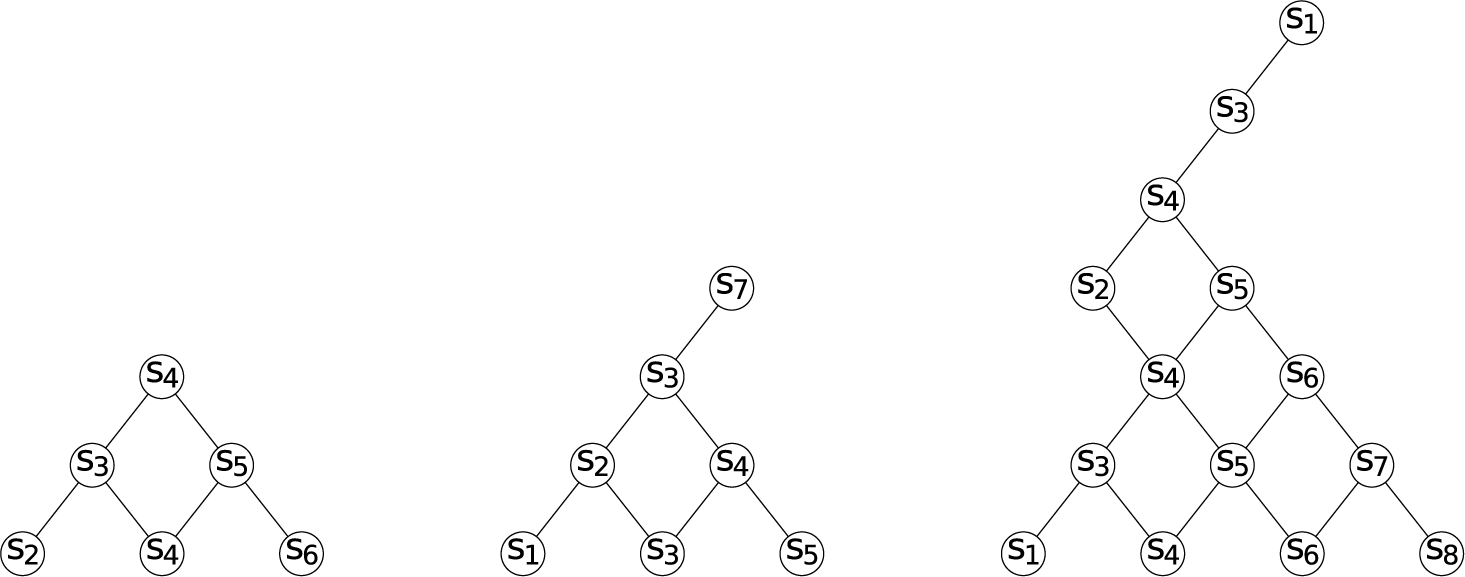
Figure 2 The heaps of the nonnesting elements of types
![]() $D_8$
,
$D_8$
,
![]() $E_7$
, and
$E_7$
, and
![]() $E_8$
.
$E_8$
.
Since
![]() $w_N=w$
is fully commutative, the elements in the set
$w_N=w$
is fully commutative, the elements in the set
![]() $\{v\in W:v\le _L w_N\}$
are in bijection with the order filters of the heap poset of
$\{v\in W:v\le _L w_N\}$
are in bijection with the order filters of the heap poset of
![]() $w_N$
. (See [Reference Stembridge54, Section 2.2] for the definition of the heap poset; an order filter of a poset P is a subset of P such that
$w_N$
. (See [Reference Stembridge54, Section 2.2] for the definition of the heap poset; an order filter of a poset P is a subset of P such that
![]() $y \in I$
whenever the conditions
$y \in I$
whenever the conditions
![]() $y \in P$
,
$y \in P$
,
![]() $x \in I$
, and
$x \in I$
, and
![]() $x \leq y$
hold.) These filters are in canonical correspondence with Dyck paths of order k, (i.e. staircase walks from
$x \leq y$
hold.) These filters are in canonical correspondence with Dyck paths of order k, (i.e. staircase walks from
![]() $(0, 0)$
to
$(0, 0)$
to
![]() $(k, k)$
that lie strictly below (but may touch) the diagonal
$(k, k)$
that lie strictly below (but may touch) the diagonal
![]() $y=x$
). It is well known [Reference Stanley53, Theorem 1.5.1 (vi)] that the number of such paths is the k-th Catalan number,
$y=x$
). It is well known [Reference Stanley53, Theorem 1.5.1 (vi)] that the number of such paths is the k-th Catalan number,
![]() $C_k=\frac {1}{k+1}\binom {2k}{k}$
. Theorem 5.13 (ii) and Theorem 5.5 imply that the number of nonnesting positive n-roots of W is given by
$C_k=\frac {1}{k+1}\binom {2k}{k}$
. Theorem 5.13 (ii) and Theorem 5.5 imply that the number of nonnesting positive n-roots of W is given by
![]() $C_k$
, as are the number of noncrossing positive n-roots and the dimension of the Macdonald representation
$C_k$
, as are the number of noncrossing positive n-roots and the dimension of the Macdonald representation
![]() $j^{\Phi }_{nA_1}({\mathrm {sgn}})$
.
$j^{\Phi }_{nA_1}({\mathrm {sgn}})$
.
The level function
![]() $\lambda $
in type
$\lambda $
in type
![]() $D_{2k}$
has a combinatorial interpretation that is natural in the context of combinatorial game theory [Reference Irie36]. The matching corresponding to an n-root
$D_{2k}$
has a combinatorial interpretation that is natural in the context of combinatorial game theory [Reference Irie36]. The matching corresponding to an n-root
![]() $\beta $
can be identified with a Steiner system
$\beta $
can be identified with a Steiner system
![]() $S(1,2,2k)$
(i.e., a collection of 2-blocks of
$S(1,2,2k)$
(i.e., a collection of 2-blocks of
![]() $[2k]$
with the property that any singleton lies in a unique 2-block). The level
$[2k]$
with the property that any singleton lies in a unique 2-block). The level
![]() $\lambda (\beta )$
then counts the number of 2-element subsets E of
$\lambda (\beta )$
then counts the number of 2-element subsets E of
![]() $[2k]$
with the property that the matching corresponding to
$[2k]$
with the property that the matching corresponding to
![]() $\beta $
contains no 2-blocks of the form
$\beta $
contains no 2-blocks of the form
![]() $(E\setminus \{j\})\cup \{i\}$
where
$(E\setminus \{j\})\cup \{i\}$
where
![]() $i\le j$
and
$i\le j$
and
![]() $j\in E$
(in particular, the matching cannot contain E). With some more work, it can be shown that each crossing gives rise to one such subset E, and each nesting gives rise to two such subsets. This gives a combinatorial interpretation of the formula
$j\in E$
(in particular, the matching cannot contain E). With some more work, it can be shown that each crossing gives rise to one such subset E, and each nesting gives rise to two such subsets. This gives a combinatorial interpretation of the formula
![]() $\lambda (x) = C(x)+2N(x)$
, and also explains the appearance of the product of odd quantum integers in [Reference Irie36, Equation (4.2)]. In addition, the quantity
$\lambda (x) = C(x)+2N(x)$
, and also explains the appearance of the product of odd quantum integers in [Reference Irie36, Equation (4.2)]. In addition, the quantity
![]() $C(m)+2N(m)$
associated to each matching m appears as ‘
$C(m)+2N(m)$
associated to each matching m appears as ‘
![]() $C(m)+2U(m)$
’ in the context of octabasis Laguerre polynomials in [Reference Simion and Stanton52, Sections 4 and 5], as the weight ‘
$C(m)+2U(m)$
’ in the context of octabasis Laguerre polynomials in [Reference Simion and Stanton52, Sections 4 and 5], as the weight ‘
![]() $\omega (m)$
’ in the context of Gaussian q-distributions in [Reference Díaz and Pariguan20, Theorem 4], and as ‘
$\omega (m)$
’ in the context of Gaussian q-distributions in [Reference Díaz and Pariguan20, Theorem 4], and as ‘
![]() $\textit {cov}(m)-\textit {cro}(m)$
’ in the context of q-Bessel numbers in [Reference Cheon and Jung15, Section 4].
$\textit {cov}(m)-\textit {cro}(m)$
’ in the context of q-Bessel numbers in [Reference Cheon and Jung15, Section 4].
The poset structure on the set
![]() $X_I$
in type
$X_I$
in type
![]() $D_{2k}$
coincides with a familiar one.
$D_{2k}$
coincides with a familiar one.
Proposition 6.1. Suppose W has type
![]() $D_{2k}$
. Then as a poset, the interval
$D_{2k}$
. Then as a poset, the interval
![]() $X_I = [\theta _C, \theta _N]$
in the quasiparabolic set X is canonically isomorphic to the symmetric group
$X_I = [\theta _C, \theta _N]$
in the quasiparabolic set X is canonically isomorphic to the symmetric group
![]() $S_k$
under the (strong) Bruhat order via the map
$S_k$
under the (strong) Bruhat order via the map
![]() $\varphi : S_k \rightarrow X_I$
sending each element
$\varphi : S_k \rightarrow X_I$
sending each element
![]() $\tau \in S_n$
to the n-root
$\tau \in S_n$
to the n-root
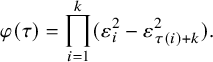 $$ \begin{align}\varphi(\tau)=\prod_{i = 1}^k (\varepsilon_i^2 - \varepsilon_{\tau(i) + k}^2). \end{align} $$
$$ \begin{align}\varphi(\tau)=\prod_{i = 1}^k (\varepsilon_i^2 - \varepsilon_{\tau(i) + k}^2). \end{align} $$
Under this bijection, we have
for every
![]() $\tau \in S_k$
, where M is the number of coplanar quadruples in each n-root and
$\tau \in S_k$
, where M is the number of coplanar quadruples in each n-root and
![]() $\ell $
denotes Coxeter length.
$\ell $
denotes Coxeter length.
Proof. By Proposition 5.2 (ii), the set
![]() $X_I$
is the
$X_I$
is the
![]() $\sigma $
-equivalence class of the n-root
$\sigma $
-equivalence class of the n-root
![]() $\theta _N$
. We noted earlier that
$\theta _N$
. We noted earlier that
![]() $\sigma (\theta _N)=2\sum _{i = 1}^k \varepsilon _i$
, which implies that n-roots in
$\sigma (\theta _N)=2\sum _{i = 1}^k \varepsilon _i$
, which implies that n-roots in
![]() $X_I$
are precisely the positive n-roots whose components are all of the form
$X_I$
are precisely the positive n-roots whose components are all of the form
![]() $\varepsilon _i \pm \varepsilon _j$
, where
$\varepsilon _i \pm \varepsilon _j$
, where
![]() $1 \leq i \leq k < j \leq 2k$
. These are precisely the n-roots listed in the theorem, so the map
$1 \leq i \leq k < j \leq 2k$
. These are precisely the n-roots listed in the theorem, so the map
![]() $\varphi $
is surjective. It is clear that
$\varphi $
is surjective. It is clear that
![]() $\varphi $
is also injective, so
$\varphi $
is also injective, so
![]() $\varphi $
is a bijection.
$\varphi $
is a bijection.
The Bruhat order on
![]() $S_k$
is generated by relations of the form
$S_k$
is generated by relations of the form
![]() $\tau < r\tau $
where we have
$\tau < r\tau $
where we have
![]() $\tau \in S_k$
and r is a reflection
$\tau \in S_k$
and r is a reflection
![]() $r=(\tau (i),\tau (j))\in S_k$
for some
$r=(\tau (i),\tau (j))\in S_k$
for some
![]() $i<j$
such that
$i<j$
such that
![]() $\tau (i)<\tau (j)$
[Reference Humphreys33, Section 5.9, Example 2]. In this case, the quadruple
$\tau (i)<\tau (j)$
[Reference Humphreys33, Section 5.9, Example 2]. In this case, the quadruple
![]() $\{\varepsilon _i\pm \varepsilon _{\tau (i)+k}, \varepsilon _j\pm \varepsilon _{\tau (j)+k}\}$
contained in
$\{\varepsilon _i\pm \varepsilon _{\tau (i)+k}, \varepsilon _j\pm \varepsilon _{\tau (j)+k}\}$
contained in
![]() $\varphi (\tau )$
is a crossing and is moved to the nesting
$\varphi (\tau )$
is a crossing and is moved to the nesting
![]() $\{\varepsilon _i\pm \varepsilon _{\tau (j)+k}, \varepsilon _j\pm \varepsilon _{\tau (i)+k}\}$
, so we have
$\{\varepsilon _i\pm \varepsilon _{\tau (j)+k}, \varepsilon _j\pm \varepsilon _{\tau (i)+k}\}$
, so we have
![]() $\lambda (\varphi (\tau ))<\lambda (r\varphi (\tau ))$
in
$\lambda (\varphi (\tau ))<\lambda (r\varphi (\tau ))$
in
![]() $X_I$
by Proposition 4.7 (iii). Conversely, if we have
$X_I$
by Proposition 4.7 (iii). Conversely, if we have
![]() $\lambda (\varphi (\tau ))<\lambda (r\varphi (\tau ))$
in
$\lambda (\varphi (\tau ))<\lambda (r\varphi (\tau ))$
in
![]() $X_I$
for some
$X_I$
for some
![]() $\tau \in S_k$
and some reflection
$\tau \in S_k$
and some reflection
![]() $r\in W$
, then since
$r\in W$
, then since
![]() $\varphi (\tau )$
has no alignments, r must move a crossing in
$\varphi (\tau )$
has no alignments, r must move a crossing in
![]() $\varphi (\tau )$
to a nesting by Proposition 4.7 (iii). The crossing moved must be of the form
$\varphi (\tau )$
to a nesting by Proposition 4.7 (iii). The crossing moved must be of the form
![]() $\{\varepsilon _i\pm \varepsilon _{\tau (i)+k}, \varepsilon _j\pm \varepsilon _{\tau (j)+k}\}$
for some
$\{\varepsilon _i\pm \varepsilon _{\tau (i)+k}, \varepsilon _j\pm \varepsilon _{\tau (j)+k}\}$
for some
![]() $i,j\in [k]$
such that
$i,j\in [k]$
such that
![]() $i<j$
and
$i<j$
and
![]() $\tau (i)<\tau (j)$
, and the only possibilities for r are
$\tau (i)<\tau (j)$
, and the only possibilities for r are
![]() $(ij)$
and
$(ij)$
and
![]() $(\tau (i)+k,\tau (j)+k)$
. In either case, we have
$(\tau (i)+k,\tau (j)+k)$
. In either case, we have
![]() $r\varphi (\tau )=\varphi (r'\tau )$
for the reflection
$r\varphi (\tau )=\varphi (r'\tau )$
for the reflection
![]() $r'=(\tau (i),\tau (j))\in S_k$
, so that we have
$r'=(\tau (i),\tau (j))\in S_k$
, so that we have
where
![]() $<$
denotes the Bruhat order in
$<$
denotes the Bruhat order in
![]() $S_k$
. It now follows that
$S_k$
. It now follows that
![]() $\varphi $
is a poset isomorphism.
$\varphi $
is a poset isomorphism.
To prove the last assertion, we note that each inversion of a permutation
![]() $\tau \in S_k$
corresponds to a nesting in the corresponding alignment-free n-root
$\tau \in S_k$
corresponds to a nesting in the corresponding alignment-free n-root
![]() $\gamma =\varphi (\tau )$
, and we recall that
$\gamma =\varphi (\tau )$
, and we recall that
![]() $\ell (\tau )$
equals the number of inversions in
$\ell (\tau )$
equals the number of inversions in
![]() $\tau $
. It follows that
$\tau $
. It follows that
![]() $N(\gamma )=\ell (\tau )$
; therefore, we have
$N(\gamma )=\ell (\tau )$
; therefore, we have
We now discuss the structure of the space
![]() $j^{D_n}_{nA_1}({\mathrm {sgn}})$
underlying the Macdonald representation as an
$j^{D_n}_{nA_1}({\mathrm {sgn}})$
underlying the Macdonald representation as an
![]() $S_{2k}$
-module. As a vector space,
$S_{2k}$
-module. As a vector space,
![]() $j^{D_n}_{nA_1}({\mathrm {sgn}})$
is isomorphic to the free vector space on the noncrossing perfect matchings of
$j^{D_n}_{nA_1}({\mathrm {sgn}})$
is isomorphic to the free vector space on the noncrossing perfect matchings of
![]() $[n]=[2k]$
, which is denoted by
$[n]=[2k]$
, which is denoted by
![]() $V(n,k,0)$
in the work of Rhoades [Reference Rhoades47]. Furthermore, given a simple reflection
$V(n,k,0)$
in the work of Rhoades [Reference Rhoades47]. Furthermore, given a simple reflection
![]() $s_i=(i,i+1)\in S_{n}$
and a noncrossing perfect matching m corresponding to an n-root
$s_i=(i,i+1)\in S_{n}$
and a noncrossing perfect matching m corresponding to an n-root
![]() $\gamma $
, the reflection
$\gamma $
, the reflection
![]() $s_i$
acts on m in one of the following ways:
$s_i$
acts on m in one of the following ways:
-
(1) if
 $i(i+1)$
is a 2-block in m, then the n-root
$i(i+1)$
is a 2-block in m, then the n-root
 $\gamma $
contains
$\gamma $
contains
 $\varepsilon _i^2-\varepsilon _{i+1}^2$
as a factor, so
$\varepsilon _i^2-\varepsilon _{i+1}^2$
as a factor, so
 $s_i(m)=-m$
;
$s_i(m)=-m$
; -
(2) if
 $i(i+1)$
if not a 2-block in m, then m contains two blocks
$i(i+1)$
if not a 2-block in m, then m contains two blocks
 $ia$
and
$ia$
and
 $(i+1)b$
which either form an alignment (if
$(i+1)b$
which either form an alignment (if
 $a<i<i+1<b$
) or a nesting (if
$a<i<i+1<b$
) or a nesting (if
 $b<a<i$
or
$b<a<i$
or
 $i+1<b<a$
). In all cases, we have
$i+1<b<a$
). In all cases, we have
 $s_i(m)=m"$
where
$s_i(m)=m"$
where
 $m"$
is the matching
$m"$
is the matching
 $(m\setminus \{ia,(i+1)b\})\cup \{(i+1)a,ib\}$
. Here, the blocks
$(m\setminus \{ia,(i+1)b\})\cup \{(i+1)a,ib\}$
. Here, the blocks
 $(i+1)a$
and
$(i+1)a$
and
 $ib$
form a crossing, and the Ptolemy relation
$ib$
form a crossing, and the Ptolemy relation
 $\gamma _C=\gamma _N+\gamma _A$
from Theorem 3.10 (vi) implies that (6.2)where
$\gamma _C=\gamma _N+\gamma _A$
from Theorem 3.10 (vi) implies that (6.2)where $$ \begin{align} s_i(m)=m"=m+m', \end{align} $$
$$ \begin{align} s_i(m)=m"=m+m', \end{align} $$
 $m'$
is the perfect matching
$m'$
is the perfect matching
 $m'=(m\setminus \{ia,(i+1)b\}) \cup \{i(i+1),ab\}$
. Here, the blocks
$m'=(m\setminus \{ia,(i+1)b\}) \cup \{i(i+1),ab\}$
. Here, the blocks
 $i(i+1)$
and
$i(i+1)$
and
 $ab$
form the nesting in the Ptolemy relation if
$ab$
form the nesting in the Ptolemy relation if
 $\{ia, (i+1)b\}$
is an alignment and form the alignment in the Ptolemy relation if
$\{ia, (i+1)b\}$
is an alignment and form the alignment in the Ptolemy relation if
 $\{ia, (i+1)b\}$
is a nesting. The matching
$\{ia, (i+1)b\}$
is a nesting. The matching
 $m'$
is noncrossing by Theorem 5.7 (iv).
$m'$
is noncrossing by Theorem 5.7 (iv).
It follows from the above analysis that the action of
![]() $S_{2k}$
on
$S_{2k}$
on
![]() $j^{D_n}_{nA_1}({\mathrm {sgn}})$
agrees with the action of
$j^{D_n}_{nA_1}({\mathrm {sgn}})$
agrees with the action of
![]() $S_{2k}$
on the space
$S_{2k}$
on the space
![]() $V(n,k,0)$
defined by Rhoades. The precise formula in Equation (6.2) appears in the work of Kim [Reference Kim38, Equation (1.3)]. By [Reference Rhoades47, Proposition 5.2], as an
$V(n,k,0)$
defined by Rhoades. The precise formula in Equation (6.2) appears in the work of Kim [Reference Kim38, Equation (1.3)]. By [Reference Rhoades47, Proposition 5.2], as an
![]() $S_{2k}$
module
$S_{2k}$
module
![]() $V(n,k,0)$
is isomorphic to the Specht module
$V(n,k,0)$
is isomorphic to the Specht module
![]() $S^{(k,k)}$
corresponding to the 2-row partition
$S^{(k,k)}$
corresponding to the 2-row partition
![]() $(k,k)$
, so we may summarize our discussion as follows:
$(k,k)$
, so we may summarize our discussion as follows:
Proposition 6.2. If W has type
![]() $D_{n}$
for
$D_{n}$
for
![]() $n=2k$
even, then the W-action on the Macdonald representation
$n=2k$
even, then the W-action on the Macdonald representation
![]() $j^{D_n}_{nA_1}({\mathrm {sgn}})$
factors through the map
$j^{D_n}_{nA_1}({\mathrm {sgn}})$
factors through the map
![]() $\phi $
defined by Equation (2.2) to induce an
$\phi $
defined by Equation (2.2) to induce an
![]() $S_n$
-module structure on
$S_n$
-module structure on
![]() $j^{D_n}_{nA_1}({\mathrm {sgn}})$
. The resulting
$j^{D_n}_{nA_1}({\mathrm {sgn}})$
. The resulting
![]() $S_n$
-module is isomorphic to the Specht module
$S_n$
-module is isomorphic to the Specht module
![]() $S^{(k,k)}\cong V(n,k,0)$
. In particular, it is irreducible.
$S^{(k,k)}\cong V(n,k,0)$
. In particular, it is irreducible.
Remark 6.3. The nonnesting and noncrossing bases for the
![]() $S_n$
-module
$S_n$
-module
![]() $j^{D_n}_{nA_1}({\mathrm {sgn}})\cong S^{(k,k)}$
are also studied extensively in the works of Russell–Tymoczko [Reference Russell and Tymoczko48], Im–Zhu [Reference Im and Zhu35], Hwang–Jang–Oh [Reference Hwang, Jang and Oh34] and Heard–Kujawa [Reference Heard and Kujawa32]. In these papers, the noncrossing basis is called the web basis, and the nonnesting basis can be naturally identified with the standard basis (or the polytabloid or Specht basis) as explained in [Reference Im and Zhu35, Lemma 3.1] and [Reference Hwang, Jang and Oh34, Section 1]. Under this identification, the isomorphism of [Reference Russell and Tymoczko48, Theorem 2.2] associates each nonnesting perfect matching with the unique noncrossing matching in the same
$j^{D_n}_{nA_1}({\mathrm {sgn}})\cong S^{(k,k)}$
are also studied extensively in the works of Russell–Tymoczko [Reference Russell and Tymoczko48], Im–Zhu [Reference Im and Zhu35], Hwang–Jang–Oh [Reference Hwang, Jang and Oh34] and Heard–Kujawa [Reference Heard and Kujawa32]. In these papers, the noncrossing basis is called the web basis, and the nonnesting basis can be naturally identified with the standard basis (or the polytabloid or Specht basis) as explained in [Reference Im and Zhu35, Lemma 3.1] and [Reference Hwang, Jang and Oh34, Section 1]. Under this identification, the isomorphism of [Reference Russell and Tymoczko48, Theorem 2.2] associates each nonnesting perfect matching with the unique noncrossing matching in the same
![]() $\sigma $
-equivalence class, and Theorem 5.5 of [Reference Russell and Tymoczko48] follows from Theorem 5.16 as a special case. The restriction of the quasiparabolic order to the noncrossing basis gives rise to the web graph of [Reference Russell and Tymoczko48, Section 2.3], which therefore has the structure of a distributive lattice by Theorem 5.13 (ii). Our definition of the nesting number (Definition 4.2 (i)) agrees with the nesting number of [Reference Russell and Tymoczko48] when restricted to noncrossing n-roots, and is inspired by [Reference Russell and Tymoczko48]. It also follows from [Reference Hwang, Jang and Oh34, Corollary 4.2] that if W has type
$\sigma $
-equivalence class, and Theorem 5.5 of [Reference Russell and Tymoczko48] follows from Theorem 5.16 as a special case. The restriction of the quasiparabolic order to the noncrossing basis gives rise to the web graph of [Reference Russell and Tymoczko48, Section 2.3], which therefore has the structure of a distributive lattice by Theorem 5.13 (ii). Our definition of the nesting number (Definition 4.2 (i)) agrees with the nesting number of [Reference Russell and Tymoczko48] when restricted to noncrossing n-roots, and is inspired by [Reference Russell and Tymoczko48]. It also follows from [Reference Hwang, Jang and Oh34, Corollary 4.2] that if W has type
![]() $D_{2k}$
and we expand the maximally crossing n-root
$D_{2k}$
and we expand the maximally crossing n-root
![]() $\theta _C$
as a linear combination of the noncrossing basis,
$\theta _C$
as a linear combination of the noncrossing basis,
![]() $\theta _C = \sum \lambda _\beta \beta $
, then the sum
$\theta _C = \sum \lambda _\beta \beta $
, then the sum
![]() $\sum \lambda _\beta $
of the nonnegative integers
$\sum \lambda _\beta $
of the nonnegative integers
![]() $\lambda _\beta $
is given by the number
$\lambda _\beta $
is given by the number
![]() $E_{k+1}$
in the family (1,1,1,2,5,16,272, …) of Euler numbers, which are characterized by the equation
$E_{k+1}$
in the family (1,1,1,2,5,16,272, …) of Euler numbers, which are characterized by the equation
 $$ \begin{align*}\sec(x) + \tan(x) = \sum_{i = 0}^\infty E_i \frac{x^i}{i!} .\end{align*} $$
$$ \begin{align*}\sec(x) + \tan(x) = \sum_{i = 0}^\infty E_i \frac{x^i}{i!} .\end{align*} $$
Coefficients in the expansion of the maximally crossing
![]() $2k$
-root
$2k$
-root
![]() $\theta _C$
into the noncrossing basis have a combinatorial interpretation in terms of the so-called web permutations in
$\theta _C$
into the noncrossing basis have a combinatorial interpretation in terms of the so-called web permutations in
![]() $S_k$
by [Reference Hwang, Jang and Oh34, Theorem 1.2].
$S_k$
by [Reference Hwang, Jang and Oh34, Theorem 1.2].
6.2 Type
 $E_7$
$E_7$
Suppose W has type
![]() $E_7$
. We define
$E_7$
. We define
![]() $\nu _A$
to be the positive
$\nu _A$
to be the positive
![]() $7$
-root with the following components:
$7$
-root with the following components:
We define
![]() $\nu _C$
to be the positive
$\nu _C$
to be the positive
![]() $7$
-root with the following components:
$7$
-root with the following components:
We define
![]() $\nu _N$
to be the positive 7-root with the following components:
$\nu _N$
to be the positive 7-root with the following components:
Finally, we define the element
![]() $w\in W$
to be the element expressed by the word
$w\in W$
to be the element expressed by the word
The heap of w is shown in Figure 2 (b).
Proposition 6.4. If W has type
![]() $E_7$
, then the
$E_7$
, then the
![]() $7$
-roots
$7$
-roots
![]() $\nu _A$
,
$\nu _A$
,
![]() $\nu _C$
and
$\nu _C$
and
![]() $\nu _N$
given above are respectively the maximally aligned, maximally crossing and maximally nesting
$\nu _N$
given above are respectively the maximally aligned, maximally crossing and maximally nesting
![]() $7$
-roots of W. The element w is the nonnesting element
$7$
-roots of W. The element w is the nonnesting element
![]() $w_N$
, and
$w_N$
, and
![]() $\mathbf {w}$
a reduced word for it. The Macdonald representation
$\mathbf {w}$
a reduced word for it. The Macdonald representation
![]() $j^{E_7}_{7A_1}({\mathrm {sgn}})$
has dimension
$j^{E_7}_{7A_1}({\mathrm {sgn}})$
has dimension
![]() $15$
.
$15$
.
Proof. Recall from Corollary 3.19 that the number of coplanar quadruples in any
![]() $7$
-root is
$7$
-root is
![]() $M=7$
. Direct verification shows that
$M=7$
. Direct verification shows that
![]() $\textrm {ht}(\sigma (\nu _C)) - \textrm {ht}(\sigma (\nu _A))=49-35 = 2M$
and that
$\textrm {ht}(\sigma (\nu _C)) - \textrm {ht}(\sigma (\nu _A))=49-35 = 2M$
and that
![]() $w(\nu _C)=\nu _A$
, which implies the assertions about
$w(\nu _C)=\nu _A$
, which implies the assertions about
![]() $\nu _A$
,
$\nu _A$
,
![]() $\nu _C$
,
$\nu _C$
,
![]() $\mathbf {w}$
and w by Theorem 5.13 (iii). The dimension of the Macdonald representation
$\mathbf {w}$
and w by Theorem 5.13 (iii). The dimension of the Macdonald representation
![]() $j^{E_7}_{7A_1}({\mathrm {sgn}})$
equals the cardinality of the set
$j^{E_7}_{7A_1}({\mathrm {sgn}})$
equals the cardinality of the set
![]() $\{v\in W: v\le _L w\}$
by Theorem 5.5 (i) and Theorem 5.13 (ii). As explained in Section 6.1, this set is in bijection with the order filters of the heap of the fully commutative
$\{v\in W: v\le _L w\}$
by Theorem 5.5 (i) and Theorem 5.13 (ii). As explained in Section 6.1, this set is in bijection with the order filters of the heap of the fully commutative
![]() $w_N$
, and direct computation shows that this heap has 15 filters, so the dimension of
$w_N$
, and direct computation shows that this heap has 15 filters, so the dimension of
![]() $j^{E_7}_{7A_1}({\mathrm {sgn}})$
is 15.
$j^{E_7}_{7A_1}({\mathrm {sgn}})$
is 15.
It remains to show that
![]() $\nu _N$
is the maximally aligned n-root
$\nu _N$
is the maximally aligned n-root
![]() $\theta _A$
. By inspection, the heights of the components of
$\theta _A$
. By inspection, the heights of the components of
![]() $\nu _N$
are 1, 5, 7, 9, 9, 9, 9 when listed in increasing order. The sum of the first three terms of this sequence is bigger than the largest term, so
$\nu _N$
are 1, 5, 7, 9, 9, 9, 9 when listed in increasing order. The sum of the first three terms of this sequence is bigger than the largest term, so
![]() $\nu _N$
cannot contain any alignments by Proposition 3.13 (ii). If
$\nu _N$
cannot contain any alignments by Proposition 3.13 (ii). If
![]() $\nu _N$
contains a crossing, it follows from Proposition 3.13 (iv) that the crossing cannot contain any component of height 1, and that the crossing can contain at most one component of height 9. It then follows from the listed heights that
$\nu _N$
contains a crossing, it follows from Proposition 3.13 (iv) that the crossing cannot contain any component of height 1, and that the crossing can contain at most one component of height 9. It then follows from the listed heights that
![]() $\nu _N$
contains no crossing either. It follows that all the M coplanar quadruples in
$\nu _N$
contains no crossing either. It follows that all the M coplanar quadruples in
![]() $\nu _N$
are nestings, so that
$\nu _N$
are nestings, so that
![]() $\nu _N=\theta _N$
by Proposition 4.11 (ii).
$\nu _N=\theta _N$
by Proposition 4.11 (ii).
The set
![]() $X_I$
of alignment-free positive
$X_I$
of alignment-free positive
![]() $7$
-roots in type
$7$
-roots in type
![]() $E_7$
is intimately related to the combinatorics of the Fano plane (Figure 3), the finite projective plane of order 2 over the field
$E_7$
is intimately related to the combinatorics of the Fano plane (Figure 3), the finite projective plane of order 2 over the field
![]() $\mathbb {F}_2$
with two elements. We recall that any two points in the Fano share a unique line that contains them both, so that the vertex labellings of the Fano points using the labels
$\mathbb {F}_2$
with two elements. We recall that any two points in the Fano share a unique line that contains them both, so that the vertex labellings of the Fano points using the labels
![]() $1,2,..,7$
correspond precisely to the Steiner triple systems
$1,2,..,7$
correspond precisely to the Steiner triple systems
![]() $S(2,3,7)$
via the bijection that associates each line in the Fano plane with the triple of labels for the vertices in that line. For example, the labellings shown in Figure 3 (a) and (b) correspond respectively to the Steiner systems
$S(2,3,7)$
via the bijection that associates each line in the Fano plane with the triple of labels for the vertices in that line. For example, the labellings shown in Figure 3 (a) and (b) correspond respectively to the Steiner systems
![]() $L_C$
and
$L_C$
and
![]() $L_N$
from Proposition 6.5. It is well known that the automorphism group of the Fano plane is the simple group
$L_N$
from Proposition 6.5. It is well known that the automorphism group of the Fano plane is the simple group
![]() $GL(3, 2)$
of order
$GL(3, 2)$
of order
![]() $168$
, so that the number of inequivalent vertex labellings is
$168$
, so that the number of inequivalent vertex labellings is
![]() $7!/168=30$
.
$7!/168=30$
.
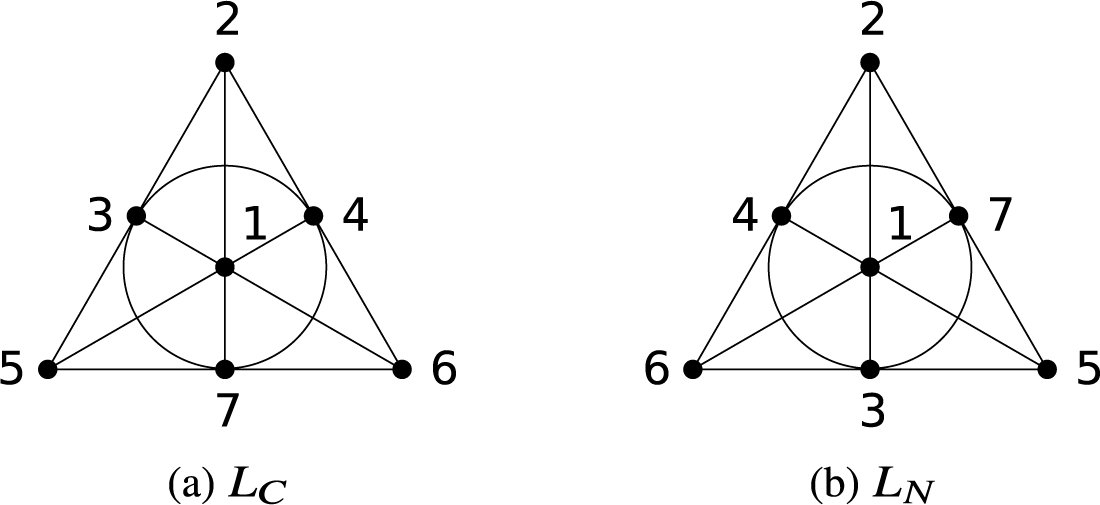
Figure 3 The inequivalent labellings of the Fano plane corresponding to
![]() $\theta _C$
and
$\theta _C$
and
![]() $\theta _N$
.
$\theta _N$
.
Proposition 6.5. If W has type
![]() $E_7$
, then every component of every 7-root
$E_7$
, then every component of every 7-root
![]() $\gamma \in X_I$
has the form
$\gamma \in X_I$
has the form
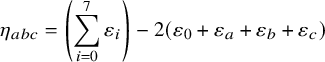 $$\begin{align*}\eta_{abc}= \left( \sum_{i = 0}^7 \varepsilon_i \right) - 2 (\varepsilon_0 + \varepsilon_a + \varepsilon_b + \varepsilon_c) \end{align*}$$
$$\begin{align*}\eta_{abc}= \left( \sum_{i = 0}^7 \varepsilon_i \right) - 2 (\varepsilon_0 + \varepsilon_a + \varepsilon_b + \varepsilon_c) \end{align*}$$
for a 3-element subset
![]() $abc:=\{a,b,c\}$
of the set [7], and the map
$abc:=\{a,b,c\}$
of the set [7], and the map
![]() $\varphi $
sending each 7-root
$\varphi $
sending each 7-root
![]() $\gamma \in X_I$
to the set
$\gamma \in X_I$
to the set
gives a canonical bijection from
![]() $X_I$
to the 30 inequivalent labellings of the Fano plane. Under this bijection, the minimal element
$X_I$
to the 30 inequivalent labellings of the Fano plane. Under this bijection, the minimal element
![]() $\theta _C$
of
$\theta _C$
of
![]() $X_I$
corresponds to the labelling
$X_I$
corresponds to the labelling
and the maximal element
![]() $\theta _N$
corresponds to the labelling
$\theta _N$
corresponds to the labelling
Proof. In the Fano coordinates, the components of the maximally crossing and maximally nesting n-roots
![]() $\theta _C$
and
$\theta _C$
and
![]() $\theta _N$
are given by the rows of the following matrices
$\theta _N$
are given by the rows of the following matrices
![]() $M_C$
and
$M_C$
and
![]() $M_N$
, respectively, where each ‘
$M_N$
, respectively, where each ‘
![]() $+$
’ stands for 1 and each ‘
$+$
’ stands for 1 and each ‘
![]() $-$
’ stands for
$-$
’ stands for
![]() $-1$
for brevity.
$-1$
for brevity.
 $$ \begin{align} M_C = \left[ \begin{matrix} {\text{--}} & {\text{--}} & {\text{+}} & {\text{--}} & {\text{+}} & {\text{+}} & {\text{--}} & {\text{+}}\\ {\text{--}} & {\text{--}} & {\text{+}} & {\text{+}} & {\text{--}} & {\text{--}} & {\text{+}} & {\text{+}}\\ {\text{--}} & {\text{--}} & {\text{--}} & {\text{+}} & {\text{+}} & {\text{+}} & {\text{+}} & {\text{--}}\\ {\text{--}} & {\text{+}} & {\text{--}} & {\text{--}} & {\text{+}} & {\text{--}} & {\text{+}} & {\text{+}}\\ {\text{--}} & {\text{+}} & {\text{--}} & {\text{+}} & {\text{--}} & {\text{+}} & {\text{--}} & {\text{+}}\\ {\text{--}} & {\text{+}} & {\text{+}} & {\text{--}} & {\text{--}} & {\text{+}} & {\text{+}} & {\text{--}}\\ {\text{--}} & {\text{+}} & {\text{+}} & {\text{+}} & {\text{+}} & {\text{--}} & {\text{--}} & {\text{--}}\\ \end{matrix} \right], \; M_N = \left[ \begin{matrix} {\text{--}} & {\text{--}} & {\text{--}} & {\text{--}} & {\text{+}} & {\text{+}} & {\text{+}} & {\text{+}}\\ {\text{--}} & {\text{--}} & {\text{+}} & {\text{+}} & {\text{--}} & {\text{--}} & {\text{+}} & {\text{+}}\\ {\text{--}} & {\text{+}} & {\text{--}} & {\text{+}} & {\text{--}} & {\text{+}} & {\text{--}} & {\text{+}}\\ {\text{--}} & {\text{+}} & {\text{--}} & {\text{+}} & {\text{+}} & {\text{--}} & {\text{+}} & {\text{--}}\\ {\text{--}} & {\text{+}} & {\text{+}} & {\text{--}} & {\text{--}} & {\text{+}} & {\text{+}} & {\text{--}}\\ {\text{--}} & {\text{+}} & {\text{+}} & {\text{--}} & {\text{+}} & {\text{--}} & {\text{--}} & {\text{+}}\\ {\text{--}} & {\text{--}} & {\text{+}} & {\text{+}} & {\text{+}} & {\text{+}} & {\text{--}} & {\text{--}}\\ \end{matrix} \right] \end{align} $$
$$ \begin{align} M_C = \left[ \begin{matrix} {\text{--}} & {\text{--}} & {\text{+}} & {\text{--}} & {\text{+}} & {\text{+}} & {\text{--}} & {\text{+}}\\ {\text{--}} & {\text{--}} & {\text{+}} & {\text{+}} & {\text{--}} & {\text{--}} & {\text{+}} & {\text{+}}\\ {\text{--}} & {\text{--}} & {\text{--}} & {\text{+}} & {\text{+}} & {\text{+}} & {\text{+}} & {\text{--}}\\ {\text{--}} & {\text{+}} & {\text{--}} & {\text{--}} & {\text{+}} & {\text{--}} & {\text{+}} & {\text{+}}\\ {\text{--}} & {\text{+}} & {\text{--}} & {\text{+}} & {\text{--}} & {\text{+}} & {\text{--}} & {\text{+}}\\ {\text{--}} & {\text{+}} & {\text{+}} & {\text{--}} & {\text{--}} & {\text{+}} & {\text{+}} & {\text{--}}\\ {\text{--}} & {\text{+}} & {\text{+}} & {\text{+}} & {\text{+}} & {\text{--}} & {\text{--}} & {\text{--}}\\ \end{matrix} \right], \; M_N = \left[ \begin{matrix} {\text{--}} & {\text{--}} & {\text{--}} & {\text{--}} & {\text{+}} & {\text{+}} & {\text{+}} & {\text{+}}\\ {\text{--}} & {\text{--}} & {\text{+}} & {\text{+}} & {\text{--}} & {\text{--}} & {\text{+}} & {\text{+}}\\ {\text{--}} & {\text{+}} & {\text{--}} & {\text{+}} & {\text{--}} & {\text{+}} & {\text{--}} & {\text{+}}\\ {\text{--}} & {\text{+}} & {\text{--}} & {\text{+}} & {\text{+}} & {\text{--}} & {\text{+}} & {\text{--}}\\ {\text{--}} & {\text{+}} & {\text{+}} & {\text{--}} & {\text{--}} & {\text{+}} & {\text{+}} & {\text{--}}\\ {\text{--}} & {\text{+}} & {\text{+}} & {\text{--}} & {\text{+}} & {\text{--}} & {\text{--}} & {\text{+}}\\ {\text{--}} & {\text{--}} & {\text{+}} & {\text{+}} & {\text{+}} & {\text{+}} & {\text{--}} & {\text{--}}\\ \end{matrix} \right] \end{align} $$
By inspection, the components of
![]() $\theta _C$
have the properties (a) each of them is a root of the form
$\theta _C$
have the properties (a) each of them is a root of the form
![]() $\eta _{abc}$
for some triple
$\eta _{abc}$
for some triple
![]() $abc\subseteq [7]$
, and (b) the triples corresponding to components form a Steiner triple system.
$abc\subseteq [7]$
, and (b) the triples corresponding to components form a Steiner triple system.
By Proposition 6.4, the rightmost generator appearing in
![]() $w_N$
is
$w_N$
is
![]() $s_7$
, which implies that
$s_7$
, which implies that
![]() $I = S \backslash \{s_7\}$
. It follows from Section 2.3 that
$I = S \backslash \{s_7\}$
. It follows from Section 2.3 that
![]() $W_I$
is a Weyl group of type
$W_I$
is a Weyl group of type
![]() $A_6$
, isomorphic to
$A_6$
, isomorphic to
![]() $S_7$
, and that
$S_7$
, and that
![]() $W_I$
acts on
$W_I$
acts on
![]() $X_I$
by permuting the Fano coordinates. Since all elements of
$X_I$
by permuting the Fano coordinates. Since all elements of
![]() $X_I$
are conjugate to
$X_I$
are conjugate to
![]() $\theta _C$
under the action of
$\theta _C$
under the action of
![]() $W_I$
by Proposition 5.2 (ii) and (iii), it now follows from the previous paragraph that for every 7-root
$W_I$
by Proposition 5.2 (ii) and (iii), it now follows from the previous paragraph that for every 7-root
![]() $\gamma \in X_I$
, the components of
$\gamma \in X_I$
, the components of
![]() $\gamma $
satisfy the properties (a) and (b) satisfied by the components of
$\gamma $
satisfy the properties (a) and (b) satisfied by the components of
![]() $\theta _C$
. This implies that the map
$\theta _C$
. This implies that the map
![]() $\varphi $
takes each element to a Steiner triple system (and thus one of the 30 inequivalent labellings of the Fano plane). The map
$\varphi $
takes each element to a Steiner triple system (and thus one of the 30 inequivalent labellings of the Fano plane). The map
![]() $\varphi $
is clearly injective, and it is surjective because all Steiner triple systems are isomorphic via the permutation action of
$\varphi $
is clearly injective, and it is surjective because all Steiner triple systems are isomorphic via the permutation action of
![]() $S_7$
by Remark 3.16. This proves the first sentence of the proposition. The second sentence holds by inspection of the matrices
$S_7$
by Remark 3.16. This proves the first sentence of the proposition. The second sentence holds by inspection of the matrices
![]() $M_C$
and
$M_C$
and
![]() $M_N$
.
$M_N$
.
Remark 6.6. The labellings canonically corresponding to
![]() $X_I$
have the following additional properties.
$X_I$
have the following additional properties.
-
(i) The triples
 $ijk$
in the labelling
$ijk$
in the labelling
 $L_C$
corresponding to the 7-root
$L_C$
corresponding to the 7-root
 $\theta _C$
appear in [Reference Talamini55, Section IV] as the triples indexing the ‘globally invariant linear forms’
$\theta _C$
appear in [Reference Talamini55, Section IV] as the triples indexing the ‘globally invariant linear forms’
 $\pm x_i\pm x_j\pm x_k$
of type
$\pm x_i\pm x_j\pm x_k$
of type
 $E_7$
.
$E_7$
. -
(ii) The labelling
 $L_N$
corresponding to
$L_N$
corresponding to
 $\theta _N$
is the unique labelling with the property that if the digits are written in binary, then the third digit of each triple is the bitwise exclusive or (XOR) of the other two.
$\theta _N$
is the unique labelling with the property that if the digits are written in binary, then the third digit of each triple is the bitwise exclusive or (XOR) of the other two. -
(iii) Recall from Remark 5.3 that
 $X_I$
naturally splits into two equal-sized components that are interchanged by the action of a reflection in
$X_I$
naturally splits into two equal-sized components that are interchanged by the action of a reflection in
 $W_I$
. As discussed in [Reference Saniga50], any two distinct labellings in the same component have precisely one triple in common.
$W_I$
. As discussed in [Reference Saniga50], any two distinct labellings in the same component have precisely one triple in common. -
(iv) The level
 $\lambda (\gamma )$
of each 7-root
$\lambda (\gamma )$
of each 7-root
 $\gamma $
in
$\gamma $
in
 $X_I$
equals
$X_I$
equals
 $(14-d)$
, where d is the number of 3-element subsets E of the set
$(14-d)$
, where d is the number of 3-element subsets E of the set
 $[7]$
with the property that the labelling
$[7]$
with the property that the labelling
 $L_\gamma $
contains no blocks of the form
$L_\gamma $
contains no blocks of the form
 $(E\setminus \{j\})\cup \{i\}$
where
$(E\setminus \{j\})\cup \{i\}$
where
 $i\le j$
and
$i\le j$
and
 $j\in E$
. This fact can be verified computationally, and is similar to the interpretation of the level function in type
$j\in E$
. This fact can be verified computationally, and is similar to the interpretation of the level function in type
 $D_{2k}$
via Steiner systems
$D_{2k}$
via Steiner systems
 $S(1,2,2k)$
given in Section 6.1.
$S(1,2,2k)$
given in Section 6.1.
Remark 6.7. The noncrossing basis in type
![]() $E_7$
is illustrated by the diagram labelled
$E_7$
is illustrated by the diagram labelled
![]() ${\mathfrak M}_6$
in [Reference Chen and Shi14, Appendix], where each rectangle can be identified with a noncrossing basis element
${\mathfrak M}_6$
in [Reference Chen and Shi14, Appendix], where each rectangle can be identified with a noncrossing basis element
![]() $\beta $
. A label of i on a rectangle indicates that
$\beta $
. A label of i on a rectangle indicates that
![]() $\alpha _i | \beta $
, i.e., that
$\alpha _i | \beta $
, i.e., that
![]() $\alpha _i$
is a component of
$\alpha _i$
is a component of
![]() $\beta $
. The edges connecting rectangles refer to star operations in the sense of [Reference Kazhdan and Lusztig37], which can be interpreted directly in terms of n-roots as follows. If i and j are adjacent vertices of the Dynkin diagram, then two noncrossing basis elements
$\beta $
. The edges connecting rectangles refer to star operations in the sense of [Reference Kazhdan and Lusztig37], which can be interpreted directly in terms of n-roots as follows. If i and j are adjacent vertices of the Dynkin diagram, then two noncrossing basis elements
![]() $\beta $
and
$\beta $
and
![]() $\beta '$
such that
$\beta '$
such that
![]() $\alpha _i | \beta $
and
$\alpha _i | \beta $
and
![]() $\alpha _j | \beta '$
are joined by an edge if we have
$\alpha _j | \beta '$
are joined by an edge if we have
![]() $s_is_j(\beta ) = \beta '$
or, equivalently,
$s_is_j(\beta ) = \beta '$
or, equivalently,
![]() $s_js_i(\beta ') = \beta $
. (A similar construction appears in [Reference Green and Xu30, Lemma 2.8].) Note that the Dynkin diagram of type
$s_js_i(\beta ') = \beta $
. (A similar construction appears in [Reference Green and Xu30, Lemma 2.8].) Note that the Dynkin diagram of type
![]() $E_7$
in [Reference Chen and Shi14] differs from the Dynkin diagram of type
$E_7$
in [Reference Chen and Shi14] differs from the Dynkin diagram of type
![]() $E_7$
shown in Figure 1 (d) in the labelling of vertices, but it can be obtained by removing the vertex ‘8’ and its incident edge from the Dynkin diagram of type
$E_7$
shown in Figure 1 (d) in the labelling of vertices, but it can be obtained by removing the vertex ‘8’ and its incident edge from the Dynkin diagram of type
![]() $E_8$
shown in Figure 1 (e).
$E_8$
shown in Figure 1 (e).
Remark 6.8. Ren–Sam–Schrader–Sturmfels [Reference Ren, Sam, Schrader and Sturmfels46, Theorem 4.1] give an ‘utterly explicit’ basis for the 15-dimensional Macdonald representation in type
![]() $E_7$
that is natural in the context of the Göpel variety in algebraic geometry. The elements of the nonnesting basis and the noncrossing basis in type
$E_7$
that is natural in the context of the Göpel variety in algebraic geometry. The elements of the nonnesting basis and the noncrossing basis in type
![]() $E_7$
all factorize into linear factors in
$E_7$
all factorize into linear factors in
![]() $\textrm {Sym}(V^*)$
by construction, but not all the basis elements of [Reference Ren, Sam, Schrader and Sturmfels46, Theorem 4.1] do, even after extending scalars to
$\textrm {Sym}(V^*)$
by construction, but not all the basis elements of [Reference Ren, Sam, Schrader and Sturmfels46, Theorem 4.1] do, even after extending scalars to
![]() ${\mathbb C}$
. It follows that the basis of [Reference Ren, Sam, Schrader and Sturmfels46] is not the same as either the noncrossing basis or the nonnesting basis, even after applying a change of basis of
${\mathbb C}$
. It follows that the basis of [Reference Ren, Sam, Schrader and Sturmfels46] is not the same as either the noncrossing basis or the nonnesting basis, even after applying a change of basis of
![]() $V^*$
.
$V^*$
.
6.3 Type
 $E_8$
$E_8$
Suppose W has type
![]() $E_8$
. We define
$E_8$
. We define
![]() $\nu _A$
to be the positive
$\nu _A$
to be the positive
![]() $8$
-root with the following components:
$8$
-root with the following components:
We define
![]() $\nu _C$
to be the positive
$\nu _C$
to be the positive
![]() $8$
-root with the following components:
$8$
-root with the following components:
We define
![]() $\nu _N$
to be the positive
$\nu _N$
to be the positive
![]() $8$
-root with the following components:
$8$
-root with the following components:
Finally, we define the element
![]() $w\in W$
to be the element expressed by the word
$w\in W$
to be the element expressed by the word
The heap of w is shown in Figure 2 (c).
Proposition 6.9. If W has type
![]() $E_8$
, then the
$E_8$
, then the
![]() $8$
-roots
$8$
-roots
![]() $\nu _A$
,
$\nu _A$
,
![]() $\nu _C$
and
$\nu _C$
and
![]() $\nu _N$
given above are respectively the maximally aligned, maximally crossing and maximally nesting
$\nu _N$
given above are respectively the maximally aligned, maximally crossing and maximally nesting
![]() $8$
-roots of W. The element w is the nonnesting element
$8$
-roots of W. The element w is the nonnesting element
![]() $w_N$
, and
$w_N$
, and
![]() $\mathbf {w}$
a reduced word for it. The Macdonald representation
$\mathbf {w}$
a reduced word for it. The Macdonald representation
![]() $j^{E_8}_{8A_1}({\mathrm {sgn}})$
has dimension
$j^{E_8}_{8A_1}({\mathrm {sgn}})$
has dimension
![]() $50$
.
$50$
.
Proof. The statements can be proved using the same strategy used in the proof of Proposition 6.4 except for the following changes in numerical details. The number M of coplanar quadruples in an n-root is now 14, and the number of order filters in the heap of the nonnesting element
![]() $w_N$
is 50. The components of
$w_N$
is 50. The components of
![]() $\nu _N$
have heights 1, 7, 11, 13, 15, 15, 15 and 15, which implies that
$\nu _N$
have heights 1, 7, 11, 13, 15, 15, 15 and 15, which implies that
![]() $\nu _N$
has no alignments by Proposition 3.13 (ii). Furthermore, if
$\nu _N$
has no alignments by Proposition 3.13 (ii). Furthermore, if
![]() $\nu _N$
had a crossing, then Proposition 3.13 (iv) implies that the only possibility would be for the crossing to contain roots of heights 7, 11, 13, and 15, but this is not possible either because
$\nu _N$
had a crossing, then Proposition 3.13 (iv) implies that the only possibility would be for the crossing to contain roots of heights 7, 11, 13, and 15, but this is not possible either because
![]() $11+13> 7+15$
.
$11+13> 7+15$
.
Remark 6.10.
-
(i) Schmidt [Reference Schmidt51, Lemma 3.4] gives an explicit partition of the 120 positive-negative pairs of roots in type
 $E_8$
into 15 sets of size 8. The components of
$E_8$
into 15 sets of size 8. The components of
 $\theta _A$
,
$\theta _A$
,
 $\theta _N$
and
$\theta _N$
and
 $\theta _C$
appear in Schmidt’s list as
$\theta _C$
appear in Schmidt’s list as
 $V_1$
,
$V_1$
,
 $V_{14}$
and
$V_{14}$
and
 $V_{15}$
, respectively.
$V_{15}$
, respectively. -
(ii) In standard coordinates, the components of the maximally crossing and maximally nesting
 $8$
-roots
$8$
-roots
 $\theta _C=\nu _C$
and
$\theta _C=\nu _C$
and
 $\theta _N=\nu _N$
are given by the rows of the following matrices
$\theta _N=\nu _N$
are given by the rows of the following matrices
 $M^{\prime }_C$
and
$M^{\prime }_C$
and
 $M^{\prime }_N$
, respectively, where each ‘
$M^{\prime }_N$
, respectively, where each ‘
 $+$
’ stands for 1 and each ‘
$+$
’ stands for 1 and each ‘
 $-$
’ stands for
$-$
’ stands for
 $-1$
for brevity.
$-1$
for brevity.  $$\begin{align*}M^{\prime}_C = \left[ \begin{matrix} {\text{+}} & {\text{+}} & {\text{--}} & {\text{--}} & {\text{--}} & {\text{--}} & {\text{+}} & {\text{+}}\\ {\text{+}} & {\text{--}} & {\text{+}} & {\text{--}} & {\text{--}} & {\text{+}} & {\text{--}} & {\text{+}}\\ {\text{+}} & {\text{--}} & {\text{--}} & {\text{+}} & {\text{+}} & {\text{--}} & {\text{--}} & {\text{+}}\\ {\text{--}} & {\text{+}} & {\text{+}} & {\text{--}} & {\text{+}} & {\text{--}} & {\text{--}} & {\text{+}}\\ {\text{--}} & {\text{+}} & {\text{--}} & {\text{+}} & {\text{--}} & {\text{+}} & {\text{--}} & {\text{+}}\\ {\text{--}} & {\text{--}} & {\text{+}} & {\text{+}} & {\text{--}} & {\text{--}} & {\text{+}} & {\text{+}}\\ {\text{--}} & {\text{--}} & {\text{--}} & {\text{--}} & {\text{+}} & {\text{+}} & {\text{+}} & {\text{+}}\\ {\text{+}} & {\text{+}} & {\text{+}} & {\text{+}} & {\text{+}} & {\text{+}} & {\text{+}} & {\text{+}}\\ \end{matrix} \right], \; M^{\prime}_N = \left[ \begin{matrix} {\text{+}} & {\text{--}} & {\text{--}} & {\text{--}} & {\text{--}} & {\text{--}} & {\text{--}} & {\text{+}}\\ {\text{--}} & {\text{+}} & {\text{+}} & {\text{+}} & {\text{--}} & {\text{--}} & {\text{--}} & {\text{+}}\\ {\text{--}} & {\text{+}} & {\text{--}} & {\text{--}} & {\text{+}} & {\text{+}} & {\text{--}} & {\text{+}}\\ {\text{--}} & {\text{--}} & {\text{+}} & {\text{--}} & {\text{+}} & {\text{--}} & {\text{+}} & {\text{+}}\\ {\text{--}} & {\text{--}} & {\text{--}} & {\text{+}} & {\text{--}} & {\text{+}} & {\text{+}} & {\text{+}}\\ {\text{+}} & {\text{+}} & {\text{+}} & {\text{--}} & {\text{--}} & {\text{+}} & {\text{+}} & {\text{+}}\\ {\text{+}} & {\text{+}} & {\text{--}} & {\text{+}} & {\text{+}} & {\text{--}} & {\text{+}} & {\text{+}}\\ {\text{+}} & {\text{--}} & {\text{+}} & {\text{+}} & {\text{+}} & {\text{+}} & {\text{--}} & {\text{+}}\\ \end{matrix} \right] \end{align*}$$
$$\begin{align*}M^{\prime}_C = \left[ \begin{matrix} {\text{+}} & {\text{+}} & {\text{--}} & {\text{--}} & {\text{--}} & {\text{--}} & {\text{+}} & {\text{+}}\\ {\text{+}} & {\text{--}} & {\text{+}} & {\text{--}} & {\text{--}} & {\text{+}} & {\text{--}} & {\text{+}}\\ {\text{+}} & {\text{--}} & {\text{--}} & {\text{+}} & {\text{+}} & {\text{--}} & {\text{--}} & {\text{+}}\\ {\text{--}} & {\text{+}} & {\text{+}} & {\text{--}} & {\text{+}} & {\text{--}} & {\text{--}} & {\text{+}}\\ {\text{--}} & {\text{+}} & {\text{--}} & {\text{+}} & {\text{--}} & {\text{+}} & {\text{--}} & {\text{+}}\\ {\text{--}} & {\text{--}} & {\text{+}} & {\text{+}} & {\text{--}} & {\text{--}} & {\text{+}} & {\text{+}}\\ {\text{--}} & {\text{--}} & {\text{--}} & {\text{--}} & {\text{+}} & {\text{+}} & {\text{+}} & {\text{+}}\\ {\text{+}} & {\text{+}} & {\text{+}} & {\text{+}} & {\text{+}} & {\text{+}} & {\text{+}} & {\text{+}}\\ \end{matrix} \right], \; M^{\prime}_N = \left[ \begin{matrix} {\text{+}} & {\text{--}} & {\text{--}} & {\text{--}} & {\text{--}} & {\text{--}} & {\text{--}} & {\text{+}}\\ {\text{--}} & {\text{+}} & {\text{+}} & {\text{+}} & {\text{--}} & {\text{--}} & {\text{--}} & {\text{+}}\\ {\text{--}} & {\text{+}} & {\text{--}} & {\text{--}} & {\text{+}} & {\text{+}} & {\text{--}} & {\text{+}}\\ {\text{--}} & {\text{--}} & {\text{+}} & {\text{--}} & {\text{+}} & {\text{--}} & {\text{+}} & {\text{+}}\\ {\text{--}} & {\text{--}} & {\text{--}} & {\text{+}} & {\text{--}} & {\text{+}} & {\text{+}} & {\text{+}}\\ {\text{+}} & {\text{+}} & {\text{+}} & {\text{--}} & {\text{--}} & {\text{+}} & {\text{+}} & {\text{+}}\\ {\text{+}} & {\text{+}} & {\text{--}} & {\text{+}} & {\text{+}} & {\text{--}} & {\text{+}} & {\text{+}}\\ {\text{+}} & {\text{--}} & {\text{+}} & {\text{+}} & {\text{+}} & {\text{+}} & {\text{--}} & {\text{+}}\\ \end{matrix} \right] \end{align*}$$
All rows in
 $M^{\prime }_C$
other than the bottom row contain four ‘
$M^{\prime }_C$
other than the bottom row contain four ‘
 $+$
’ and four ‘
$+$
’ and four ‘
 $-$
’, and the 14 quadruples recording the column numbers of the positive and negative entries in these rows form a Steiner quadruple system. Furthermore, these 14 quadruples are precisely the ones indexing the ‘globally invariant linear forms’ of type
$-$
’, and the 14 quadruples recording the column numbers of the positive and negative entries in these rows form a Steiner quadruple system. Furthermore, these 14 quadruples are precisely the ones indexing the ‘globally invariant linear forms’ of type
 $E_8$
in [Reference Talamini55, Section V].
$E_8$
in [Reference Talamini55, Section V]. -
(iii) The matrix
 $M^{\prime }_C$
above is a Hadamard matrix, meaning a matrix with entries in
$M^{\prime }_C$
above is a Hadamard matrix, meaning a matrix with entries in
 $\{+1, -1\}$
that has orthogonal rows (and, therefore, orthogonal columns). By rearranging the rows, the matrix can be expressed more simply as the Kronecker product
$\{+1, -1\}$
that has orthogonal rows (and, therefore, orthogonal columns). By rearranging the rows, the matrix can be expressed more simply as the Kronecker product
 $H \otimes H \otimes H$
, where
$H \otimes H \otimes H$
, where  $$ \begin{align*}H = \left[ \begin{matrix} \text{+1} & \text{+1} \\ \text{--1} & \text{+1} \end{matrix} \right].\end{align*} $$
$$ \begin{align*}H = \left[ \begin{matrix} \text{+1} & \text{+1} \\ \text{--1} & \text{+1} \end{matrix} \right].\end{align*} $$
Remark 6.11. The noncrossing basis in type
![]() $E_8$
is illustrated by the diagram labelled
$E_8$
is illustrated by the diagram labelled
![]() ${\mathfrak M}_{50}$
in [Reference Chen13, Appendix].
${\mathfrak M}_{50}$
in [Reference Chen13, Appendix].
The set
![]() $X_I$
of alignment-free positive
$X_I$
of alignment-free positive
![]() $8$
-roots in type
$8$
-roots in type
![]() $E_8$
can be used to give a convenient realization of the graph
$E_8$
can be used to give a convenient realization of the graph
![]() $\bar \Gamma _1$
studied by Schmidt in [Reference Schmidt51]. The graph
$\bar \Gamma _1$
studied by Schmidt in [Reference Schmidt51]. The graph
![]() $\bar \Gamma _1$
, which is the complement of another graph
$\bar \Gamma _1$
, which is the complement of another graph
![]() $\Gamma _1$
, has the property that it is quantum isomorphic (in the sense of [Reference Atserias, Mančinska, Roberson, Šámal, Severini and Varvitsiotis3]) but not isomorphic to the orthogonality graph
$\Gamma _1$
, has the property that it is quantum isomorphic (in the sense of [Reference Atserias, Mančinska, Roberson, Šámal, Severini and Varvitsiotis3]) but not isomorphic to the orthogonality graph
![]() $G_{E_8}$
of the roots of type
$G_{E_8}$
of the roots of type
![]() $E_8$
. The vertices of
$E_8$
. The vertices of
![]() $G_{E_8}$
are the 120 positive roots of type
$G_{E_8}$
are the 120 positive roots of type
![]() $E_8$
, and two roots are adjacent in
$E_8$
, and two roots are adjacent in
![]() $G_{E_8}$
if and only if they are orthogonal.
$G_{E_8}$
if and only if they are orthogonal.
To realize the graph
![]() $\bar \Gamma _1$
via
$\bar \Gamma _1$
via
![]() $X_I$
, recall from Remark 5.3 that
$X_I$
, recall from Remark 5.3 that
![]() $X_I$
naturally splits into two equal-sized components,
$X_I$
naturally splits into two equal-sized components,
![]() $X_I^e$
and
$X_I^e$
and
![]() $X_I^o$
, which consist of all the elements in
$X_I^o$
, which consist of all the elements in
![]() $X_I$
with even levels and odd levels, respectively. The components each have
$X_I$
with even levels and odd levels, respectively. The components each have
![]() $240/2=120$
elements since
$240/2=120$
elements since
![]() $\lvert X_I \rvert =240$
by Proposition 7.1 (ii).
$\lvert X_I \rvert =240$
by Proposition 7.1 (ii).
Definition 6.12. We define
![]() $\Gamma $
to be the following graph: the vertex set is
$\Gamma $
to be the following graph: the vertex set is
![]() $X_I^e$
, the set of all alignment-free positive
$X_I^e$
, the set of all alignment-free positive
![]() $8$
-roots of even parabolic level, and two vertices are adjacent if and only if they have no common components.
$8$
-roots of even parabolic level, and two vertices are adjacent if and only if they have no common components.
The next four paragraphs recall Schmidt’s construction of the graph
![]() $\Gamma _1$
and explain why
$\Gamma _1$
and explain why
![]() $\Gamma $
is isomorphic to
$\Gamma $
is isomorphic to
![]() $\bar \Gamma _1$
. (The isomorphism will also hold if we replace
$\bar \Gamma _1$
. (The isomorphism will also hold if we replace
![]() $X_I^e$
with
$X_I^e$
with
![]() $X_I^o$
in Definition 6.12.)
$X_I^o$
in Definition 6.12.)
Start with the folded halved 8-cube, where the vertices are the 64 pairs of the form
![]() $\{x,\mathbf {1}+x\}$
for all length-8 binary strings
$\{x,\mathbf {1}+x\}$
for all length-8 binary strings
![]() $x\in \mathbb {F}_2^8$
with an even number of 1s (where
$x\in \mathbb {F}_2^8$
with an even number of 1s (where
![]() $\mathbf {1}$
is the string with all entries equal to
$\mathbf {1}$
is the string with all entries equal to
![]() $1$
). We can naturally identify these vertices with the 64 positive roots of the form
$1$
). We can naturally identify these vertices with the 64 positive roots of the form
![]() $\alpha =(\sum _{i=1}^7\pm \varepsilon _i)+\varepsilon _8$
, via the bijection sending
$\alpha =(\sum _{i=1}^7\pm \varepsilon _i)+\varepsilon _8$
, via the bijection sending
![]() $\alpha $
to the pair
$\alpha $
to the pair
![]() $\{x_\alpha ,\mathbf {1}+x_\alpha \}$
where
$\{x_\alpha ,\mathbf {1}+x_\alpha \}$
where
![]() $x_\alpha $
is the string
$x_\alpha $
is the string
![]() $(x_i)_{i=1}^8$
such that
$(x_i)_{i=1}^8$
such that
![]() $x_i=1$
if and only if
$x_i=1$
if and only if
![]() $\varepsilon _i$
appears with coefficient
$\varepsilon _i$
appears with coefficient
![]() $-1$
in
$-1$
in
![]() $\alpha $
for all
$\alpha $
for all
![]() $i\in [8]$
. The 64 positive roots of the form
$i\in [8]$
. The 64 positive roots of the form
![]() $(\sum _{i=1}^7\pm \varepsilon _i)+\varepsilon _8$
are precisely the positive roots of x-height 1 in the sense of Remark 5.3, so they are also precisely the roots that can appear as a component of an 8-root in
$(\sum _{i=1}^7\pm \varepsilon _i)+\varepsilon _8$
are precisely the positive roots of x-height 1 in the sense of Remark 5.3, so they are also precisely the roots that can appear as a component of an 8-root in
![]() $X_I$
by Remark 5.3.
$X_I$
by Remark 5.3.
By definition, two vertices
![]() $\{x,\mathbf {1}+x\}$
and
$\{x,\mathbf {1}+x\}$
and
![]() $\{y,\mathbf {1}+y\}$
in the folded halved cube are adjacent if and only if x and y differ in 2 or 6 entries. It follows that in the complement of the folded halved cube, two distinct vertices
$\{y,\mathbf {1}+y\}$
in the folded halved cube are adjacent if and only if x and y differ in 2 or 6 entries. It follows that in the complement of the folded halved cube, two distinct vertices
![]() $\{x,\mathbf {1}+x\}$
and
$\{x,\mathbf {1}+x\}$
and
![]() $\{y,\mathbf {1}+y\}$
are adjacent if and only if x and y differ in 4 positions. This complement is denoted
$\{y,\mathbf {1}+y\}$
are adjacent if and only if x and y differ in 4 positions. This complement is denoted
![]() $VO_6^+(2)$
. The condition that x and y differ in 4 entries holds if and only if the positive roots corresponding to
$VO_6^+(2)$
. The condition that x and y differ in 4 entries holds if and only if the positive roots corresponding to
![]() $\{x,\mathbf {1}+x\}$
and
$\{x,\mathbf {1}+x\}$
and
![]() $\{y,\mathbf {1}+y\}$
are orthogonal; therefore, each clique of size 8 in
$\{y,\mathbf {1}+y\}$
are orthogonal; therefore, each clique of size 8 in
![]() $VO_6^+(2)$
corresponds to an 8-root in
$VO_6^+(2)$
corresponds to an 8-root in
![]() $X_I$
.
$X_I$
.
Schmidt defines the vertex set of
![]() $\Gamma _1$
to be any orbit of cliques of size 8 under the group
$\Gamma _1$
to be any orbit of cliques of size 8 under the group
![]() ${\mathbb Z}_2^6\rtimes A_8$
in
${\mathbb Z}_2^6\rtimes A_8$
in
![]() $VO_6^+(2)$
, where
$VO_6^+(2)$
, where
![]() $A_8$
is the alternating subgroup of
$A_8$
is the alternating subgroup of
![]() $S_8$
. There are two such orbits, both of size 120, and the choice of the orbit does not matter, so we may assume that the orbit contains a clique corresponding to an 8-root with even level, that is, to a vertex,
$S_8$
. There are two such orbits, both of size 120, and the choice of the orbit does not matter, so we may assume that the orbit contains a clique corresponding to an 8-root with even level, that is, to a vertex,
![]() $\beta $
, of
$\beta $
, of
![]() $\Gamma $
. The vertices of
$\Gamma $
. The vertices of
![]() $\Gamma _1$
then match precisely the vertices of
$\Gamma _1$
then match precisely the vertices of
![]() $\Gamma $
for the reasons sketched below. We have
$\Gamma $
for the reasons sketched below. We have
![]() $I=S\setminus \{s_1\}$
by Proposition 6.9; therefore, we have
$I=S\setminus \{s_1\}$
by Proposition 6.9; therefore, we have
![]() $W_I\cong W(D_7)$
. The action of
$W_I\cong W(D_7)$
. The action of
![]() $W_I = W(D_7)$
on
$W_I = W(D_7)$
on
![]() $X_I$
can be extended to an action of a larger subgroup
$X_I$
can be extended to an action of a larger subgroup
![]() $G \leq W(E_8)$
, generated by
$G \leq W(E_8)$
, generated by
![]() $W_I$
together with the reflection
$W_I$
together with the reflection
![]() $s_\theta $
corresponding to the highest root
$s_\theta $
corresponding to the highest root
![]() $\theta =2(\varepsilon _7+\varepsilon _8)$
. We have
$\theta =2(\varepsilon _7+\varepsilon _8)$
. We have
![]() $G \cong W(D_8) \cong N \rtimes S_8$
, where
$G \cong W(D_8) \cong N \rtimes S_8$
, where
![]() $N \cong {\mathbb Z}_2^7$
is the elementary abelian group of order
$N \cong {\mathbb Z}_2^7$
is the elementary abelian group of order
![]() $2^7$
. By considerations involving x-heights (in the sense of Remark 5.3), each reflection in G changes every 8-root in
$2^7$
. By considerations involving x-heights (in the sense of Remark 5.3), each reflection in G changes every 8-root in
![]() $X_I$
, and when it does so, it changes the parabolic level by an odd number because it moves a C to an N or vice versa. It follows that the commutator subgroup
$X_I$
, and when it does so, it changes the parabolic level by an odd number because it moves a C to an N or vice versa. It follows that the commutator subgroup
![]() $G'\cong {\mathbb Z}_2^7\rtimes A_8$
of G acts on
$G'\cong {\mathbb Z}_2^7\rtimes A_8$
of G acts on
![]() $X_I$
with
$X_I$
with
![]() $X_I^{e}$
and
$X_I^{e}$
and
![]() $X_I^{o}$
as its orbits. This action induces a transitive action of
$X_I^{o}$
as its orbits. This action induces a transitive action of
![]() $G'/Z(G) \cong {\mathbb Z}_2^6\rtimes A_8$
on
$G'/Z(G) \cong {\mathbb Z}_2^6\rtimes A_8$
on
![]() $\Gamma $
that matches the action of
$\Gamma $
that matches the action of
![]() ${\mathbb Z}_2^6\rtimes A_8$
on
${\mathbb Z}_2^6\rtimes A_8$
on
![]() $\Gamma _1$
.
$\Gamma _1$
.
Two vertices in
![]() $\Gamma _1$
are defined to be adjacent if and only if they are cliques that intersect in exactly two elements from
$\Gamma _1$
are defined to be adjacent if and only if they are cliques that intersect in exactly two elements from
![]() $VO_6^+(2)$
. This occurs if and only if their corresponding
$VO_6^+(2)$
. This occurs if and only if their corresponding
![]() $8$
-roots have two components in common. With some more work, or using computation, one can show that two distinct 8-roots whose levels have the same parity either have disjoint components or have exactly two components in common. It follows that
$8$
-roots have two components in common. With some more work, or using computation, one can show that two distinct 8-roots whose levels have the same parity either have disjoint components or have exactly two components in common. It follows that
![]() $\Gamma $
is isomorphic to
$\Gamma $
is isomorphic to
![]() $\bar \Gamma _1$
. To summarize, we have the following result.
$\bar \Gamma _1$
. To summarize, we have the following result.
Remark 6.13. The graph
![]() $\Gamma $
from Definition 6.12 (i.e., the graph whose vertices are the alignment-free positive
$\Gamma $
from Definition 6.12 (i.e., the graph whose vertices are the alignment-free positive
![]() $8$
-roots of even parabolic level and where two vertices are adjacent if and only if they have no common component) is isomorphic to the graph
$8$
-roots of even parabolic level and where two vertices are adjacent if and only if they have no common component) is isomorphic to the graph
![]() $\bar \Gamma _1$
from [Reference Schmidt51]. As a consequence, the graph
$\bar \Gamma _1$
from [Reference Schmidt51]. As a consequence, the graph
![]() $\Gamma $
is quantum isomorphic but not isomorphic to the orthogonality graph
$\Gamma $
is quantum isomorphic but not isomorphic to the orthogonality graph
![]() $G_{E_8}$
of the
$G_{E_8}$
of the
![]() $E_8$
root system.
$E_8$
root system.
The graphs
![]() $\Gamma _{E_8}$
and
$\Gamma _{E_8}$
and
![]() $\bar \Gamma _1$
are known to be strongly regular graphs with parameters
$\bar \Gamma _1$
are known to be strongly regular graphs with parameters
![]() $(120, 63, 30, 36)$
. It follows that
$(120, 63, 30, 36)$
. It follows that
![]() $\Gamma $
is also such a graph. Mathon and Street [Reference Mathon and Street40, Table 2.2] mention that the graphs
$\Gamma $
is also such a graph. Mathon and Street [Reference Mathon and Street40, Table 2.2] mention that the graphs
![]() $\Gamma _{E_8}$
and
$\Gamma _{E_8}$
and
![]() $\bar \Gamma _1$
each have 2025
$\bar \Gamma _1$
each have 2025
![]() $8$
-cliques. The 8-cliques of
$8$
-cliques. The 8-cliques of
![]() $\Gamma _{E_8}$
are the positive
$\Gamma _{E_8}$
are the positive
![]() $8$
-roots of
$8$
-roots of
![]() $E_8$
, and the 8-cliques of
$E_8$
, and the 8-cliques of
![]() $\Gamma \cong \bar \Gamma _1$
are classified by Fitz in [Reference Fitz24, Theorem 7.6]. Finally, we note that, as [Reference Schmidt51] points out, there are other constructions of
$\Gamma \cong \bar \Gamma _1$
are classified by Fitz in [Reference Fitz24, Theorem 7.6]. Finally, we note that, as [Reference Schmidt51] points out, there are other constructions of
![]() $\Gamma _1$
in the literature [Reference Brouwer, Ivanov and Klin8, Reference Mathon and Street40]. However, the construction in terms of
$\Gamma _1$
in the literature [Reference Brouwer, Ivanov and Klin8, Reference Mathon and Street40]. However, the construction in terms of
![]() $8$
-roots has the advantages of being concise, and being clearly related to the
$8$
-roots has the advantages of being concise, and being clearly related to the
![]() $E_8$
root system.
$E_8$
root system.
Remark 6.14. The group
![]() $\textrm {Aut}(\Gamma _1)$
acts as a permutation group of rank 4 on
$\textrm {Aut}(\Gamma _1)$
acts as a permutation group of rank 4 on
![]() $\Gamma _1$
[Reference Brouwer, Ivanov and Klin8]. It follows that if two n-roots
$\Gamma _1$
[Reference Brouwer, Ivanov and Klin8]. It follows that if two n-roots
![]() $x,y\in X_I$
both have even or odd levels, then x and y can be in one of four relative positions. These can be shown to be the following (where N is the elementary abelian group of order
$x,y\in X_I$
both have even or odd levels, then x and y can be in one of four relative positions. These can be shown to be the following (where N is the elementary abelian group of order
![]() $2^7$
mentioned above):
$2^7$
mentioned above):
-
(i)
 $x=y$
;
$x=y$
; -
(ii) x and y have precisely two common components;
-
(iii) x and y have disjoint components, and
 $y = n.x$
for some
$y = n.x$
for some
 $n \in N$
;
$n \in N$
; -
(iv) x and y have disjoint components, and
 $y \ne n.x$
for any
$y \ne n.x$
for any
 $n \in N$
.
$n \in N$
.
The situations in (iii) and (iv) correspond to the edges in the graph
![]() $\Gamma $
, and they show that the edges of
$\Gamma $
, and they show that the edges of
![]() $\Gamma $
naturally split into two types. This is not the case for the graph
$\Gamma $
naturally split into two types. This is not the case for the graph
![]() $G_{E_8}$
: the automorphism group of
$G_{E_8}$
: the automorphism group of
![]() $G_{E_8}$
has rank 3, and two vertices can only be in three relative positions: equality, adjacency and non-adjacency.
$G_{E_8}$
has rank 3, and two vertices can only be in three relative positions: equality, adjacency and non-adjacency.
7 Concluding remarks
7.1 Poincaré polynomials
Rains and Vazirani [Reference Rains and Vazirani43, Section 8] define the Poincaré series of a quasiparabolic set
![]() $\mathcal {X}$
to be
$\mathcal {X}$
to be
![]() $PS(q) = \sum _{x \in \mathcal {X}}q^{\lambda (x)}$
. They point out that in many cases, the Poincaré series factorizes in a very simple way, and the factors are often quantum integers
$PS(q) = \sum _{x \in \mathcal {X}}q^{\lambda (x)}$
. They point out that in many cases, the Poincaré series factorizes in a very simple way, and the factors are often quantum integers
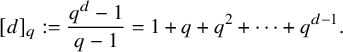 $$ \begin{align*}[d]_q := \frac{q^d-1}{q-1} = 1 + q + q^2 + \cdots + q^{d-1} .\end{align*} $$
$$ \begin{align*}[d]_q := \frac{q^d-1}{q-1} = 1 + q + q^2 + \cdots + q^{d-1} .\end{align*} $$
These quantum integers often behave as if they were the degrees of polynomial invariants of a Coxeter group, and in some cases, the integers can be interpreted in terms of degrees of invariants in characteristic 2 (see [Reference Rains and Vazirani43, Section 8, Example 9.4]).
Proposition 7.1. Let W be a Weyl group of type
![]() $E_7, E_8$
or
$E_7, E_8$
or
![]() $D_n$
for n even.
$D_n$
for n even.
-
(i) For the quasiparabolic set X for W consisting of all positive n-roots of W, equipped with the level function such that
 $\lambda (\theta _A)=0$
, we have
$\lambda (\theta _A)=0$
, we have  $$ \begin{align*}PS_X(q) = \begin{cases} \prod_{i = 2}^k [2i-1]_q & \text{\ if \ } W \text{\ is\ of\ type\ } D_{2k},\\ [3]_q[5]_q[9]_q & \text{\ if \ } W \text{\ is\ of\ type\ } E_7, \\ [3]_q[5]_q[9]_q[15]_q & \text{\ if \ } W \text{\ is\ of\ type\ } E_8. \end{cases}\end{align*} $$
$$ \begin{align*}PS_X(q) = \begin{cases} \prod_{i = 2}^k [2i-1]_q & \text{\ if \ } W \text{\ is\ of\ type\ } D_{2k},\\ [3]_q[5]_q[9]_q & \text{\ if \ } W \text{\ is\ of\ type\ } E_7, \\ [3]_q[5]_q[9]_q[15]_q & \text{\ if \ } W \text{\ is\ of\ type\ } E_8. \end{cases}\end{align*} $$
-
(ii) For the quasiparabolic set
 $X_I\subseteq X$
for
$X_I\subseteq X$
for
 $W_I$
consisting of the alignment-free positive n-roots of W (with its level function inherited from X), we have where M is the level
$W_I$
consisting of the alignment-free positive n-roots of W (with its level function inherited from X), we have where M is the level
 $\lambda (\theta _C)$
of the minimal element of
$\lambda (\theta _C)$
of the minimal element of
 $X_I$
(which is also the number of coplanar quadruples in each n-root). In particular, each of the factors
$X_I$
(which is also the number of coplanar quadruples in each n-root). In particular, each of the factors
 $[i]_q$
of
$[i]_q$
of
 $PS_{X_I}(q)$
corresponds to a factor
$PS_{X_I}(q)$
corresponds to a factor
 $[2i-1]_q$
of
$[2i-1]_q$
of
 $PS_X(q)$
in (i).
$PS_X(q)$
in (i).
Proof. We have verified both (i) and (ii) in types
![]() $E_7$
and
$E_7$
and
![]() $E_8$
computationally. (We do not have conceptual proofs at the moment.) For type
$E_8$
computationally. (We do not have conceptual proofs at the moment.) For type
![]() $D_n$
, part (i) follows from [Reference Simion and Stanton52, Equation (5.4)], or [Reference Díaz and Pariguan20, Theorem 4] or [Reference Cheon and Jung15, Corollary 3.3], after we identify X with the perfect matchings of the set
$D_n$
, part (i) follows from [Reference Simion and Stanton52, Equation (5.4)], or [Reference Díaz and Pariguan20, Theorem 4] or [Reference Cheon and Jung15, Corollary 3.3], after we identify X with the perfect matchings of the set
![]() $[n]$
as usual. Finally, part (ii) for type
$[n]$
as usual. Finally, part (ii) for type
![]() $D_n$
follows from Proposition 6.1 and the well-known form
$D_n$
follows from Proposition 6.1 and the well-known form
![]() $\prod _{i=2}^k [i]_q$
for the Poincaré series
$\prod _{i=2}^k [i]_q$
for the Poincaré series
![]() $\sum _{\tau \in S_k}q^{\ell (\tau )}$
of the symmetric group
$\sum _{\tau \in S_k}q^{\ell (\tau )}$
of the symmetric group
![]() $S_k$
.
$S_k$
.
Remark 7.2. The exponents
![]() $3, 5, 9$
and
$3, 5, 9$
and
![]() $3, 5, 9, 15$
that respectively appear in the Poincaré series
$3, 5, 9, 15$
that respectively appear in the Poincaré series
![]() $PS_X(q)$
of types
$PS_X(q)$
of types
![]() $E_7$
and
$E_7$
and
![]() $E_8$
show up as the degrees of generators in the cohomology modulo 2 of compact exceptional Lie groups [Reference Araki and Shikata2], and as the codimensions of generators of Chow rings associated to linear algebraic groups in characteristic 2 [Reference Petrov, Semenov and Zainoulline42, Section 4].
$E_8$
show up as the degrees of generators in the cohomology modulo 2 of compact exceptional Lie groups [Reference Araki and Shikata2], and as the codimensions of generators of Chow rings associated to linear algebraic groups in characteristic 2 [Reference Petrov, Semenov and Zainoulline42, Section 4].
Remark 7.3. Recall from Proposition 5.15 that the set
![]() $X_I$
is the top
$X_I$
is the top
![]() $\sigma $
-equivalence class with respect to the order
$\sigma $
-equivalence class with respect to the order
![]() $\le _\sigma $
. It turns out that for every
$\le _\sigma $
. It turns out that for every
![]() $\sigma $
-equivalence class C in X, the polynomial
$\sigma $
-equivalence class C in X, the polynomial
![]() $PS_C(q)=\sum _{x\in C}q^{\lambda (x)}$
has the form
$PS_C(q)=\sum _{x\in C}q^{\lambda (x)}$
has the form
for some set of nonnegative integers D. This is particularly remarkable because in general, there is no obvious way to turn a
![]() $\sigma $
-equivalence class into a W-set for a suitable Weyl group W. In type
$\sigma $
-equivalence class into a W-set for a suitable Weyl group W. In type
![]() $D_n$
, the integers from D have an interpretation in terms of rook placements [Reference Watson58, Theorem 1]. Summing over all
$D_n$
, the integers from D have an interpretation in terms of rook placements [Reference Watson58, Theorem 1]. Summing over all
![]() $\sigma $
-equivalence classes gives rise to the expression for
$\sigma $
-equivalence classes gives rise to the expression for
![]() $PS_X(q)$
that appears in the abstract of [Reference Billera, Levine and Mészáros6]. In types
$PS_X(q)$
that appears in the abstract of [Reference Billera, Levine and Mészáros6]. In types
![]() $E_7$
and
$E_7$
and
![]() $E_8$
, we verified Equation (7.1) by computation.
$E_8$
, we verified Equation (7.1) by computation.
7.2 Coxeter elements
Let
![]() $d_1, d_2, \ldots , d_r$
be the numbers that appear in the factorization
$d_1, d_2, \ldots , d_r$
be the numbers that appear in the factorization
![]() $\prod _{i=1}^r [d_i]_q$
of the Poincare series
$\prod _{i=1}^r [d_i]_q$
of the Poincare series
![]() $PS_X(q)$
in Proposition 7.1 (i). It follows easily from the definitions that
$PS_X(q)$
in Proposition 7.1 (i). It follows easily from the definitions that
![]() $\prod _{i=1}^r d_i$
is the number of positive n-roots, and that
$\prod _{i=1}^r d_i$
is the number of positive n-roots, and that
![]() $\sum _{i=1}^r (d_i-1) = 2M$
, where M is the number of coplanar quadruples in an n-root. It also turns out that the largest integer
$\sum _{i=1}^r (d_i-1) = 2M$
, where M is the number of coplanar quadruples in an n-root. It also turns out that the largest integer
![]() $d_r$
in each case (which is
$d_r$
in each case (which is
![]() $n-1$
in type
$n-1$
in type
![]() $D_n$
, is
$D_n$
, is
![]() $9$
in type
$9$
in type
![]() $E_7$
, and is
$E_7$
, and is
![]() $15$
in type
$15$
in type
![]() $E_8$
) is equal to
$E_8$
) is equal to
![]() $h/2$
, where h is the Coxeter number.
$h/2$
, where h is the Coxeter number.
We recall that, by definition, a Coxeter element is a product of all the simple reflections in some order, and the Coxeter number is the order of any Coxeter element c. All such elements are conjugate and therefore have the same order. It turns out that
![]() $c^{h/2}$
acts as
$c^{h/2}$
acts as
![]() $-1$
in the reflection representation, and therefore acts trivially on the set X. If C is the cyclic group of order
$-1$
in the reflection representation, and therefore acts trivially on the set X. If C is the cyclic group of order
![]() $h/2$
generated by the action of c on the positive n-roots, then it can be shown that the nonidentity elements of C act without fixed points on the positive n-roots. The factor of
$h/2$
generated by the action of c on the positive n-roots, then it can be shown that the nonidentity elements of C act without fixed points on the positive n-roots. The factor of
![]() $[h/2]_q$
in
$[h/2]_q$
in
![]() $PS_X(q)$
then implies that the triple
$PS_X(q)$
then implies that the triple
![]() $(X, PS_X(q), C)$
satisfies the cyclic sieving phenomenon of Reiner, Stanton and White [Reference Reiner, Stanton and White45]: the number of fixed points of
$(X, PS_X(q), C)$
satisfies the cyclic sieving phenomenon of Reiner, Stanton and White [Reference Reiner, Stanton and White45]: the number of fixed points of
![]() $c^d$
is equal to
$c^d$
is equal to
![]() $PS_X(e^{2\pi id/m})$
, where
$PS_X(e^{2\pi id/m})$
, where
![]() $m=h/2$
.
$m=h/2$
.
It is possible, by choosing a suitable Coxeter element c and n-root
![]() $\beta $
, to find an orbit of n-roots
$\beta $
, to find an orbit of n-roots
that contains every positive root exactly once as one of its components. This can be achieved in type
![]() $D_n$
by taking
$D_n$
by taking
![]() $\beta = \theta _N$
and
$\beta = \theta _N$
and
![]() $c = s_1 s_2 \cdots s_{n-1}s_n$
. We also verified that such an orbit can also be found in types
$c = s_1 s_2 \cdots s_{n-1}s_n$
. We also verified that such an orbit can also be found in types
![]() $E_7$
and
$E_7$
and
![]() $E_8$
, although it is necessary to make a different choice of
$E_8$
, although it is necessary to make a different choice of
![]() $\beta $
. The existence of such an orbit O in type
$\beta $
. The existence of such an orbit O in type
![]() $E_8$
is related to the Kochen–Specker theorem in quantum mechanics [Reference Waegell and Aravind57].
$E_8$
is related to the Kochen–Specker theorem in quantum mechanics [Reference Waegell and Aravind57].
7.3 Feature-avoidance via quasiparabolic structure
It can be shown that each of the three types of feature-avoiding n-roots in the set X can be characterized using only the quasiparabolic structure of X, without reference to the combinatorics of n-roots. Specifically, the following holds for all n-roots
![]() $x\in X$
:
$x\in X$
:
-
(i) x is alignment-free if and only if there does not exist a reflection r such that
 $\lambda (r(x))-\lambda (x)$
is a strictly positive even number;
$\lambda (r(x))-\lambda (x)$
is a strictly positive even number; -
(ii) x is noncrossing if and only if there is a sequence
where $$ \begin{align*}x <_Q r_1(x) <_Q r_2r_1(x) <_Q \cdots <_Q x_1,\end{align*} $$
$$ \begin{align*}x <_Q r_1(x) <_Q r_2r_1(x) <_Q \cdots <_Q x_1,\end{align*} $$
 $x_1$
is the unique maximal element of X and the level increases by
$x_1$
is the unique maximal element of X and the level increases by
 $2$
at each step;
$2$
at each step;
-
(iii) x is nonnesting if and only if there does not exist a reflection r such that
 $\lambda (r(x)) - \lambda (x)$
is a strictly negative even number.
$\lambda (r(x)) - \lambda (x)$
is a strictly negative even number.
In addition, Remark 5.17 shows that the
![]() $\sigma $
-equivalence classes can be characterized as the Eulerian intervals between nonnesting and noncrossing elements. It may be interesting to use these characterizations to extend the notions of feature-avoiding elements and
$\sigma $
-equivalence classes can be characterized as the Eulerian intervals between nonnesting and noncrossing elements. It may be interesting to use these characterizations to extend the notions of feature-avoiding elements and
![]() $\sigma $
-equivalence to more general quasiparabolic sets.
$\sigma $
-equivalence to more general quasiparabolic sets.
Acknowledgements
We are grateful to the referees for reading the paper carefully and suggesting many improvements. We also thank Dana Ernst, Emily King, Heather Russell and Nathaniel Thiem for helpful conversations.
Competing interest
The authors have no competing interests to declare.