Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-02-05T10:50:01.837Z Has data issue: false hasContentIssue false
  • English
  • Français

GENERALIZED FINITE POLYLOGARITHMS

Part of: Arithmetic algebraic geometry Other special functions

Published online by Cambridge University Press:  19 February 2020

MARINA AVITABILE  and
SANDRO MATTAREI
MARINA AVITABILE
Affiliation:
Dipartimento di Matematica e Applicazioni, Università degli Studi di Milano - Bicocca, via Cozzi 55, I-20125Milano, Italy, e-mail: marina.avitabile@unimib.it
SANDRO MATTAREI
Affiliation:
Charlotte Scott Centre for Algebra, University of Lincoln, Brayford Pool Lincoln, LN6 7TS, United Kingdom, e-mail: smattarei@lincoln.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce a generalization 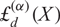${\rm{\pounds}}_d^{(\alpha)}(X)$ of the finite polylogarithms 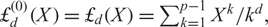${\rm{\pounds}}_d^{(0)}(X) = {{\rm{\pounds}}_d}(X) = \sum\nolimits_{k = 1}^{p - 1} {X^k}/{k^d}$ , in characteristic p, which depends on a parameter α. The special case 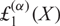${\rm{\pounds}}_1^{(\alpha)}(X)$ was previously investigated by the authors as the inverse, in an appropriate sense, of a parametrized generalization of the truncated exponential which is instrumental in a grading switching technique for nonassociative algebras. Here, we extend such generalization to 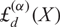${\rm{\pounds}}_d^{(\alpha)}(X)$ in a natural manner and study some properties satisfied by those polynomials. In particular, we find how the polynomials 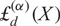${\rm{\pounds}}_d^{(\alpha)}(X)$ are related to the powers of 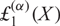${\rm{\pounds}}_1^{(\alpha)}(X)$ and derive some consequences.

MSC classification

Primary: 33E50: Special functions in characteristic $p$ (gamma functions, etc.)
Secondary: 11G55: Polylogarithms and relations with $K$-theory 39B52: Equations for functions with more general domains and/or ranges 33C45: Orthogonal polynomials and functions of hypergeometric type (Jacobi, Laguerre, Hermite, Askey scheme, etc.)
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 63 , Issue 1 , January 2021 , pp. 66 - 80
Copyright
© The Author(s) 2020. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Avitabile, M. and Mattarei, S., Grading switching for modular non-associative algebras, Lie algebras and related topics, Contemp. Math., vol. 652, Amer. Math. Soc., Providence, RI, 2015, pp. 1–14. MR 3453046Google Scholar
Avitabile, M. and Mattarei, S., Laguerre polynomials of derivations, Israel J. Math. 205 (2015), no. 1, 109–126. MR 3314584Google Scholar
Avitabile, M. and Mattarei, S., A generalized truncated logarithm, Aequationes Math. 93 (2019), no. 4, 711–734. MR 3984323Google Scholar
Elbaz-Vincent, P. and Gangl, H., On poly(ana)logs. I, Compositio Math. 130 (2002), no. 2, 161–210. MR 1883818 (2002m:11059)CrossRefGoogle Scholar
Kontsevich, M., The $1\frac{1}{2}$ -logarithm. Appendix to: “On poly(ana)logs. I” [Compositio Math 130 (2002), no. 2, 161–210; MR1883818 (2002m:11059)] by P. Elbaz-Vincent and H. Gangl, Compositio Math. 130 (2002), no. 2, 211–214. MR 1884238 (2002m:11060)Google Scholar
Mattarei, S., Artin-Hasse exponentials of derivations, J. Algebra 294 (2005), no. 1, 1–18. MR 2171626Google Scholar
Mattarei, S., Exponential functions in prime characteristic, Aequationes Math. 71 (2006), no. 3, 311–317. MR 2236408 (2007b:39056)Google Scholar
Mattarei, S. and Tauraso, R., Congruences for central binomial sums and finite polylogarithms, J. Number Theory 133 (2013), no. 1, 131–157. MR 2981405Google Scholar
Mattarei, S. and Tauraso, R., From generating series to polynomial congruences , J. Number Theory 182 (2018), 179–205. MR 3703936Google Scholar
Mirimanoff, D., L’équation indéterminée ${x^\ell } + {y^\ell } + {z^\ell } = 0$ et le critérium de Kummer, J. Reine Angew. Math. 128 (1905), 45–68. MR 1580644Google Scholar
Ribenboim, P., 13 lectures on Fermat’s last theorem, Springer-Verlag, New York, 1979. MR 551363 (81f:10023)Google Scholar