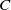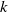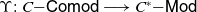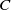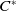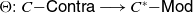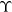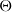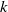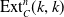1. Introduction
In this paper, we work with coassociative, counital coalgebras over a field
![]() $k$
. For any such coalgebra
$k$
. For any such coalgebra
![]() $C$
, the dual
$C$
, the dual
![]() $k$
-vector space
$k$
-vector space
![]() $C^*$
is naturally an associative, unital algebra over
$C^*$
is naturally an associative, unital algebra over
![]() $k$
. One has to choose between two opposite ways of defining the multiplication on
$k$
. One has to choose between two opposite ways of defining the multiplication on
![]() $C^*$
. We prefer the notation in which any left
$C^*$
. We prefer the notation in which any left
![]() $C$
-comodule becomes a left
$C$
-comodule becomes a left
![]() $C^*$
-module, and any right
$C^*$
-module, and any right
![]() $C$
-comodule becomes a right
$C$
-comodule becomes a right
![]() $C^*$
-module.
$C^*$
-module.
It is known, at least, since 1960s that the resulting exact functor
![]() $\Upsilon :\ C{{-\mathsf{Comod}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
is fully faithful [Reference Sweedler44, Section 2.1]. Following the terminology of the book [Reference Sweedler44],
$\Upsilon :\ C{{-\mathsf{Comod}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
is fully faithful [Reference Sweedler44, Section 2.1]. Following the terminology of the book [Reference Sweedler44],
![]() $C^*$
-modules coming from
$C^*$
-modules coming from
![]() $C$
-comodules are often called “rational” in the literature. The essential image of the functor
$C$
-comodules are often called “rational” in the literature. The essential image of the functor
![]() $\Upsilon$
is a hereditary pretorsion class in
$\Upsilon$
is a hereditary pretorsion class in
![]() $C^*{{-\mathsf{Mod}}}$
: this means that the full subcategory
$C^*{{-\mathsf{Mod}}}$
: this means that the full subcategory
![]() $\Upsilon (C{{-\mathsf{Comod}}})$
is closed under subobjects, quotient objects, and infinite coproducts in
$\Upsilon (C{{-\mathsf{Comod}}})$
is closed under subobjects, quotient objects, and infinite coproducts in
![]() $C^*{{-\mathsf{Mod}}}$
. However, this full subcategory need not be closed under extensions. In other words,
$C^*{{-\mathsf{Mod}}}$
. However, this full subcategory need not be closed under extensions. In other words,
![]() $\Upsilon (C{{-\mathsf{Comod}}})$
is not always a torsion class or a Serre subcategory in
$\Upsilon (C{{-\mathsf{Comod}}})$
is not always a torsion class or a Serre subcategory in
![]() $C^*{{-\mathsf{Mod}}}$
. A module extension of two comodules need not be a comodule.
$C^*{{-\mathsf{Mod}}}$
. A module extension of two comodules need not be a comodule.
When is the essential image of
![]() $\Upsilon$
closed under extensions in
$\Upsilon$
closed under extensions in
![]() $C^*{{-\mathsf{Mod}}}$
? There is a vast body of literature on this topic, including the papers [Reference Cuadra3, Reference Cuadra, Năstăsescu and van Oystaeyen4, Reference Iovanov10, Reference Lin15, Reference Radford41, Reference Shudo43, Reference Teply and Torrecillas46]. In this paper, we discuss further questions going in this direction, under an additional assumption. The assumption is that the coalgebra
$C^*{{-\mathsf{Mod}}}$
? There is a vast body of literature on this topic, including the papers [Reference Cuadra3, Reference Cuadra, Năstăsescu and van Oystaeyen4, Reference Iovanov10, Reference Lin15, Reference Radford41, Reference Shudo43, Reference Teply and Torrecillas46]. In this paper, we discuss further questions going in this direction, under an additional assumption. The assumption is that the coalgebra
![]() $C$
is conilpotent. The conilpotent coalgebras were called “pointed irreducible” in the terminology of [Reference Sweedler44]. For a conilpotent coalgebra
$C$
is conilpotent. The conilpotent coalgebras were called “pointed irreducible” in the terminology of [Reference Sweedler44]. For a conilpotent coalgebra
![]() $C$
, the full subcategory
$C$
, the full subcategory
![]() $C{{-\mathsf{Comod}}}$
is closed under extensions in
$C{{-\mathsf{Comod}}}$
is closed under extensions in
![]() $C^*{{-\mathsf{Mod}}}$
if and only if the coalgebra
$C^*{{-\mathsf{Mod}}}$
if and only if the coalgebra
![]() $C$
is finitely cogenerated [Reference Radford41, Corollary 2.4 and Section 2.5], [Reference Shudo43, Theorem 4.6], [Reference Lin15, Corollary 21], [Reference Cuadra, Năstăsescu and van Oystaeyen4, Theorem 2.8], [Reference Cuadra3, Proposition 3.13 and Corollary 3.14], [Reference Iovanov10, Lemma 1.2 and Theorem 4.8]. If
$C$
is finitely cogenerated [Reference Radford41, Corollary 2.4 and Section 2.5], [Reference Shudo43, Theorem 4.6], [Reference Lin15, Corollary 21], [Reference Cuadra, Năstăsescu and van Oystaeyen4, Theorem 2.8], [Reference Cuadra3, Proposition 3.13 and Corollary 3.14], [Reference Iovanov10, Lemma 1.2 and Theorem 4.8]. If
![]() $C$
is not finitely cogenerated, then there is a two-dimensional
$C$
is not finitely cogenerated, then there is a two-dimensional
![]() $C^*$
-module which is not a
$C^*$
-module which is not a
![]() $C$
-comodule, but an extension of two one-dimensional
$C$
-comodule, but an extension of two one-dimensional
![]() $C$
-comodules.
$C$
-comodules.
Let
![]() $\mathsf{A}$
and
$\mathsf{A}$
and
![]() $\mathsf{B}$
be two abelian categories, and
$\mathsf{B}$
be two abelian categories, and
![]() $\Phi :\ \mathsf{B}\longrightarrow \mathsf{A}$
be a fully faithful exact functor. Then the essential image of
$\Phi :\ \mathsf{B}\longrightarrow \mathsf{A}$
be a fully faithful exact functor. Then the essential image of
![]() $\Phi$
is a full subcategory closed under kernels and cokernels in
$\Phi$
is a full subcategory closed under kernels and cokernels in
![]() $\mathsf{A}$
. The full subcategory
$\mathsf{A}$
. The full subcategory
![]() $\Phi (\mathsf{B})$
is closed under extensions in
$\Phi (\mathsf{B})$
is closed under extensions in
![]() $\mathsf{A}$
if and only if the functor
$\mathsf{A}$
if and only if the functor
![]() $\Phi$
induces an isomorphism
$\Phi$
induces an isomorphism
for all objects
![]() $X$
,
$X$
,
![]() $Y\in \mathsf{B}$
. Generally speaking, for a fully faithful exact functor
$Y\in \mathsf{B}$
. Generally speaking, for a fully faithful exact functor
![]() $\Phi$
, the map (1) is a monomorphism, but not necessarily an isomorphism.
$\Phi$
, the map (1) is a monomorphism, but not necessarily an isomorphism.
Thus, the following question is a natural extension of the question about extension closedness of
![]() $\Upsilon (C{{-\mathsf{Comod}}})$
in
$\Upsilon (C{{-\mathsf{Comod}}})$
in
![]() $C^*{{-\mathsf{Mod}}}$
. Put
$C^*{{-\mathsf{Mod}}}$
. Put
![]() $\mathsf{B}=C{{-\mathsf{Comod}}}$
,
$\mathsf{B}=C{{-\mathsf{Comod}}}$
,
![]() $\mathsf{A}=C^*{{-\mathsf{Mod}}}$
, and
$\mathsf{A}=C^*{{-\mathsf{Mod}}}$
, and
![]() $\Phi =\Upsilon$
. Consider the induced maps on the Ext spaces
$\Phi =\Upsilon$
. Consider the induced maps on the Ext spaces
When is the map (2) in isomorphism for all
![]() $X$
,
$X$
,
![]() $Y\in \mathsf{B}$
? Generally speaking, for an exact functor of abelian categories
$Y\in \mathsf{B}$
? Generally speaking, for an exact functor of abelian categories
![]() $\Phi :\ \mathsf{B}\longrightarrow \mathsf{A}$
, all one can say is that the map (2) is a monomorphism for
$\Phi :\ \mathsf{B}\longrightarrow \mathsf{A}$
, all one can say is that the map (2) is a monomorphism for
![]() $i=n+1$
and all
$i=n+1$
and all
![]() $X$
,
$X$
,
![]() $Y\in \mathsf{B}$
whenever it is an isomorphism for
$Y\in \mathsf{B}$
whenever it is an isomorphism for
![]() $i=n$
and all
$i=n$
and all
![]() $X$
,
$X$
,
![]() $Y\in \mathsf{B}$
.
$Y\in \mathsf{B}$
.
Let
![]() $C$
be a conilpotent coalgebra over a field
$C$
be a conilpotent coalgebra over a field
![]() $k$
. Then the one-dimensional
$k$
. Then the one-dimensional
![]() $k$
-vector space
$k$
-vector space
![]() $k$
has a unique left
$k$
has a unique left
![]() $C$
-comodule structure (and a unique right
$C$
-comodule structure (and a unique right
![]() $C$
-comodule structure) provided by the unique coaugmentation of
$C$
-comodule structure) provided by the unique coaugmentation of
![]() $C$
. In this context, we show that the maps (2) are isomorphisms for
$C$
. In this context, we show that the maps (2) are isomorphisms for
![]() $\Phi =\Upsilon$
and all
$\Phi =\Upsilon$
and all
![]() $1\le i\le n$
if and only if the
$1\le i\le n$
if and only if the
![]() $k$
-vector spaces
$k$
-vector spaces
![]() $\textrm {Ext}^i_C(k,k)$
(computed in the abelian category of left or right
$\textrm {Ext}^i_C(k,k)$
(computed in the abelian category of left or right
![]() $C$
-comodules) are finite-dimensional for all
$C$
-comodules) are finite-dimensional for all
![]() $1\le i\le n$
. In particular,
$1\le i\le n$
. In particular,
![]() $\textrm {Ext}^1_C(k,k)$
is the vector space of cogenerators of a conilpotent coalgebra
$\textrm {Ext}^1_C(k,k)$
is the vector space of cogenerators of a conilpotent coalgebra
![]() $C$
; so
$C$
; so
![]() $C$
is finitely cogenerated if and only if
$C$
is finitely cogenerated if and only if
![]() $\textrm {Ext}^1_C(k,k)$
is finite-dimensional.
$\textrm {Ext}^1_C(k,k)$
is finite-dimensional.
Alongside with the abelian categories of left and right comodules over a coalgebra
![]() $C$
, there are much less familiar, but no less natural abelian categories of left and right
$C$
, there are much less familiar, but no less natural abelian categories of left and right
![]() $C$
-contramodules [Reference Positselski24]. Endowing the dual vector space
$C$
-contramodules [Reference Positselski24]. Endowing the dual vector space
![]() $C^*$
to a coalgebra
$C^*$
to a coalgebra
![]() $C$
with the natural algebra structure in which any left
$C$
with the natural algebra structure in which any left
![]() $C$
-comodule is a left
$C$
-comodule is a left
![]() $C^*$
-module and any right
$C^*$
-module and any right
![]() $C$
-comodule is a right
$C$
-comodule is a right
![]() $C^*$
-module, one also obtains a natural left
$C^*$
-module, one also obtains a natural left
![]() $C^*$
-module structure on any left
$C^*$
-module structure on any left
![]() $C$
-contramodule. So there is an exact forgetful functor
$C$
-contramodule. So there is an exact forgetful functor
![]() $\Theta :\ C{{-\mathsf{Contra}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
.
$\Theta :\ C{{-\mathsf{Contra}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
.
The functor
![]() $\Theta$
is not in general fully faithful. It was shown in the paper [Reference Positselski30, Theorem 2.1] that that the functor
$\Theta$
is not in general fully faithful. It was shown in the paper [Reference Positselski30, Theorem 2.1] that that the functor
![]() $\Theta$
is fully faithful for any finitely cogenerated conilpotent coalgebra
$\Theta$
is fully faithful for any finitely cogenerated conilpotent coalgebra
![]() $C$
. In this paper, we demonstrate a counterexample proving the (much easier) converse implication: if a conilpotent coalgebra
$C$
. In this paper, we demonstrate a counterexample proving the (much easier) converse implication: if a conilpotent coalgebra
![]() $C$
is not finitely cogenerated, then the functor
$C$
is not finitely cogenerated, then the functor
![]() $\Theta$
is not fully faithful.
$\Theta$
is not fully faithful.
More generally, the maps (2) are isomorphisms for
![]() $\Phi =\Theta$
and all
$\Phi =\Theta$
and all
![]() $0\le i\le n-1$
(for separated contramodules
$0\le i\le n-1$
(for separated contramodules
![]() $Y$
; and also for
$Y$
; and also for
![]() $0\le i\le n-2$
and arbitrary
$0\le i\le n-2$
and arbitrary
![]() $Y$
) if and only if the
$Y$
) if and only if the
![]() $k$
-vector spaces
$k$
-vector spaces
![]() $\textrm {Ext}^i_C(k,k)$
are finite-dimensional for all
$\textrm {Ext}^i_C(k,k)$
are finite-dimensional for all
![]() $1\le i\le n$
. Summarizing the assertions for comodules and contramodules, let us state the following theorem.
$1\le i\le n$
. Summarizing the assertions for comodules and contramodules, let us state the following theorem.
Theorem 1.1.
Let
![]() $C$
be a conilpotent coalgebra over a field
$C$
be a conilpotent coalgebra over a field
![]() $k$
and
$k$
and
![]() $n\ge 1$
be an integer. Then the following five conditions are equivalent:
$n\ge 1$
be an integer. Then the following five conditions are equivalent:
-
(i) the map
induced by the inclusion functor \begin{equation*} \textrm {Ext}^i_C(L,M) \longrightarrow \textrm {Ext}^i_{C^*}(L,M) \end{equation*}
\begin{equation*} \textrm {Ext}^i_C(L,M) \longrightarrow \textrm {Ext}^i_{C^*}(L,M) \end{equation*}
 $\Upsilon :\ C{{-\mathsf{Comod}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
is an isomorphism for all left
$\Upsilon :\ C{{-\mathsf{Comod}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
is an isomorphism for all left
 $C$
-comodules
$C$
-comodules
 $L$
and
$L$
and
 $M$
, and all
$M$
, and all
 $1\le i\le n$
;
$1\le i\le n$
;
-
(ii) the map
induced by the inclusion functor \begin{equation*} \textrm {Ext}^i_{C^{\mathrm{op}}}(L,M) \longrightarrow \textrm {Ext}^i_{C^*{}^{\mathrm{op}}}(L,M) \end{equation*}
\begin{equation*} \textrm {Ext}^i_{C^{\mathrm{op}}}(L,M) \longrightarrow \textrm {Ext}^i_{C^*{}^{\mathrm{op}}}(L,M) \end{equation*}
 ${{\mathsf{Comod}-}} C\longrightarrow {{\mathsf{Mod}-}} C^*$
is an isomorphism for all right
${{\mathsf{Comod}-}} C\longrightarrow {{\mathsf{Mod}-}} C^*$
is an isomorphism for all right
 $C$
-comodules
$C$
-comodules
 $L$
and
$L$
and
 $M$
, and all
$M$
, and all
 $1\le i\le n$
;
$1\le i\le n$
;
-
(iii) the map
(3)induced by the forgetful functor \begin{equation} \textrm {Ext}^{C,i}(P,Q) \longrightarrow \textrm {Ext}^i_{C^*}(P,Q) \end{equation}
\begin{equation} \textrm {Ext}^{C,i}(P,Q) \longrightarrow \textrm {Ext}^i_{C^*}(P,Q) \end{equation}
 $\Theta :\ C{{-\mathsf{Contra}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
is an isomorphism for all left
$\Theta :\ C{{-\mathsf{Contra}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
is an isomorphism for all left
 $C$
-contramodules
$C$
-contramodules
 $P$
, all separated left
$P$
, all separated left
 $C$
-contramodules
$C$
-contramodules
 $Q$
, and all
$Q$
, and all
 $0\le i\le n-1$
;
$0\le i\le n-1$
;
-
(iv) the
 $k$
-vector space
$k$
-vector space
 $\textrm {Ext}^i_C(k,k)$
is finite-dimensional for all
$\textrm {Ext}^i_C(k,k)$
is finite-dimensional for all
 $1\le i\le n$
;
$1\le i\le n$
; -
(v) the
 $k$
-vector space
$k$
-vector space
 $\textrm {Ext}^{C,i}(k,k)$
is finite-dimensional for all
$\textrm {Ext}^{C,i}(k,k)$
is finite-dimensional for all
 $1\le i\le n$
.
$1\le i\le n$
.
If any one of the equivalent conditions (i–v) holds, then the map (3) is an isomorphism for all left
![]() $C$
-contramodules
$C$
-contramodules
![]() $P$
and
$P$
and
![]() $Q$
and all
$Q$
and all
![]() $0\le i\le n-2$
.
$0\le i\le n-2$
.
Notice a curious cohomological dimension shift in comparison between the assertions about the comodule and contramodule inclusion/forgetful functors. Let
![]() $n\ge 1$
be the minimal integer for which the vector space
$n\ge 1$
be the minimal integer for which the vector space
![]() $\textrm {Ext}^n_C(k,k)$
is infinite-dimensional. Then the map
$\textrm {Ext}^n_C(k,k)$
is infinite-dimensional. Then the map
![]() $\textrm {Ext}^n_C(k,k)\longrightarrow \textrm {Ext}^n_{C^*}(k,k)$
induced by the functor
$\textrm {Ext}^n_C(k,k)\longrightarrow \textrm {Ext}^n_{C^*}(k,k)$
induced by the functor
![]() $\Upsilon$
is injective, but not surjective. In fact, the dimension cardinality of the vector space
$\Upsilon$
is injective, but not surjective. In fact, the dimension cardinality of the vector space
![]() $\textrm {Ext}^n_{C^*}(k,k)$
is larger than that of
$\textrm {Ext}^n_{C^*}(k,k)$
is larger than that of
![]() $\textrm {Ext}^n_C(k,k)$
in this case:
$\textrm {Ext}^n_C(k,k)$
in this case:
![]() $\textrm {Ext}^n_{C^*}(k,k)$
is as large as the double dual vector space
$\textrm {Ext}^n_{C^*}(k,k)$
is as large as the double dual vector space
![]() $\textrm {Ext}^n_C(k,k)^{**}$
to
$\textrm {Ext}^n_C(k,k)^{**}$
to
![]() $\textrm {Ext}^n_C(k,k)$
.
$\textrm {Ext}^n_C(k,k)$
.
At the same time, denoting by
![]() $T$
an infinite-dimensional
$T$
an infinite-dimensional
![]() $k$
-vector space endowed with the trivial
$k$
-vector space endowed with the trivial
![]() $C$
-contramodule structure, the map
$C$
-contramodule structure, the map
![]() $\textrm {Ext}^{C,n}(T,k)\longrightarrow \textrm {Ext}_{C^*}^n(T,k)$
induced by the functor
$\textrm {Ext}^{C,n}(T,k)\longrightarrow \textrm {Ext}_{C^*}^n(T,k)$
induced by the functor
![]() $\Theta$
is not injective (for the integer
$\Theta$
is not injective (for the integer
![]() $n$
as in the previous paragraph). Consequently, there exists a projective
$n$
as in the previous paragraph). Consequently, there exists a projective
![]() $C$
-contramodule
$C$
-contramodule
![]() $P$
such that the map
$P$
such that the map
![]() $\textrm {Ext}^{C,n-1}(P,k)\longrightarrow \textrm {Ext}_{C^*}^{n-1}(P,k)$
is injective, but not surjective. For
$\textrm {Ext}^{C,n-1}(P,k)\longrightarrow \textrm {Ext}_{C^*}^{n-1}(P,k)$
is injective, but not surjective. For
![]() $n\gt 1$
this, of course, means that
$n\gt 1$
this, of course, means that
![]() $\textrm {Ext}_{C^*}^{n-1}(P,k)\ne 0$
, while
$\textrm {Ext}_{C^*}^{n-1}(P,k)\ne 0$
, while
![]() $\textrm {Ext}^{C,n-1}(P,k)=0$
as it should be. Notice that both the contramodules
$\textrm {Ext}^{C,n-1}(P,k)=0$
as it should be. Notice that both the contramodules
![]() $P$
and
$P$
and
![]() $k$
are separated.
$k$
are separated.
Let us emphasize that we do not know whether the equivalent conditions (i–v) of Theorem1.1 imply bijectivity of the maps (3) for arbitrary (nonseparated) contramodules
![]() $Q$
and
$Q$
and
![]() $i=n-1$
. This remains an open question.
$i=n-1$
. This remains an open question.
Returning to the discussion of a fully faithful exact functor
![]() $\Phi :\ \mathsf{B}\longrightarrow \mathsf{A}$
, it is clear that the maps of Ext groups (2) induced by
$\Phi :\ \mathsf{B}\longrightarrow \mathsf{A}$
, it is clear that the maps of Ext groups (2) induced by
![]() $\Phi$
are isomorphisms if and only if the induced triangulated functor between the bounded derived categories
$\Phi$
are isomorphisms if and only if the induced triangulated functor between the bounded derived categories
![]() $\Phi ^{\mathsf{b}}:\ \mathsf{D}^{\mathsf{b}}(\mathsf{B})\longrightarrow \mathsf{D}^{\mathsf{b}}(\mathsf{A})$
is fully faithful. Now assume that there are enough injective objects in the abelian category
$\Phi ^{\mathsf{b}}:\ \mathsf{D}^{\mathsf{b}}(\mathsf{B})\longrightarrow \mathsf{D}^{\mathsf{b}}(\mathsf{A})$
is fully faithful. Now assume that there are enough injective objects in the abelian category
![]() $\mathsf{A}$
and the functor
$\mathsf{A}$
and the functor
![]() $\Phi :\ \mathsf{B}\longrightarrow \mathsf{A}$
has a right adjoint. Then the functor
$\Phi :\ \mathsf{B}\longrightarrow \mathsf{A}$
has a right adjoint. Then the functor
![]() $\Phi ^{\mathsf{b}}$
is fully faithful if and only if the similar functor between the bounded below derived categories
$\Phi ^{\mathsf{b}}$
is fully faithful if and only if the similar functor between the bounded below derived categories
![]() $\Phi ^+:\ \mathsf{D}^+(\mathsf{B})\longrightarrow \mathsf{D}^+(\mathsf{A})$
is fully faithful.
$\Phi ^+:\ \mathsf{D}^+(\mathsf{B})\longrightarrow \mathsf{D}^+(\mathsf{A})$
is fully faithful.
Dually, assume that there are enough projective objects in
![]() $\mathsf{A}$
and the functor
$\mathsf{A}$
and the functor
![]() $\Phi :\ \mathsf{B}\longrightarrow \mathsf{A}$
has a left adjoint. Then the functor
$\Phi :\ \mathsf{B}\longrightarrow \mathsf{A}$
has a left adjoint. Then the functor
![]() $\Phi ^{\mathsf{b}}$
is fully faithful if and only if the similar functor between the bounded above derived categories
$\Phi ^{\mathsf{b}}$
is fully faithful if and only if the similar functor between the bounded above derived categories
![]() $\Phi ^-:\ \mathsf{D}^-(\mathsf{B})\longrightarrow \mathsf{D}^-(\mathsf{A})$
is fully faithful [Reference Positselski31, Proposition 6.5].
$\Phi ^-:\ \mathsf{D}^-(\mathsf{B})\longrightarrow \mathsf{D}^-(\mathsf{A})$
is fully faithful [Reference Positselski31, Proposition 6.5].
In the situation at hand, there are enough projective and injective objects in the categories of modules over associative rings. The comodule inclusion functor
![]() $\Upsilon :\ C{{-\mathsf{Comod}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
has a right adjoint functor
$\Upsilon :\ C{{-\mathsf{Comod}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
has a right adjoint functor
![]() $\Gamma :\ C^*{{-\mathsf{Mod}}}\longrightarrow C{{-\mathsf{Comod}}}$
, while the contramodule forgetful functor
$\Gamma :\ C^*{{-\mathsf{Mod}}}\longrightarrow C{{-\mathsf{Comod}}}$
, while the contramodule forgetful functor
![]() $\Theta :\ C{{-\mathsf{Contra}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
has a left adjoint functor
$\Theta :\ C{{-\mathsf{Contra}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
has a left adjoint functor
![]() $\Delta :\ C^*{{-\mathsf{Mod}}}\longrightarrow C{{-\mathsf{Contra}}}$
. Consequently, Theorem1.1 implies the following result about full-and-faithfulness of induced triangulated functors.
$\Delta :\ C^*{{-\mathsf{Mod}}}\longrightarrow C{{-\mathsf{Contra}}}$
. Consequently, Theorem1.1 implies the following result about full-and-faithfulness of induced triangulated functors.
Theorem 1.2.
For any conilpotent coalgebra
![]() $C$
over a field
$C$
over a field
![]() $k$
, the following eight conditions are equivalent:
$k$
, the following eight conditions are equivalent:
-
(i) the triangulated functor
 $\Upsilon ^{\mathsf{b}}:\ \mathsf{D}^{\mathsf{b}}(C{{-\mathsf{Comod}}})\longrightarrow \mathsf{D}^{\mathsf{b}}(C^*{{-\mathsf{Mod}}})$
induced by the comodule inclusion functor
$\Upsilon ^{\mathsf{b}}:\ \mathsf{D}^{\mathsf{b}}(C{{-\mathsf{Comod}}})\longrightarrow \mathsf{D}^{\mathsf{b}}(C^*{{-\mathsf{Mod}}})$
induced by the comodule inclusion functor
 $\Upsilon :\ C{{-\mathsf{Comod}}} \longrightarrow C^*{{-\mathsf{Mod}}}$
is fully faithful;
$\Upsilon :\ C{{-\mathsf{Comod}}} \longrightarrow C^*{{-\mathsf{Mod}}}$
is fully faithful;
-
(ii) the triangulated functor
 $\Upsilon ^+:\ \mathsf{D}^+(C{{-\mathsf{Comod}}})\longrightarrow \mathsf{D}^+(C^*{{-\mathsf{Mod}}})$
induced by the comodule inclusion functor
$\Upsilon ^+:\ \mathsf{D}^+(C{{-\mathsf{Comod}}})\longrightarrow \mathsf{D}^+(C^*{{-\mathsf{Mod}}})$
induced by the comodule inclusion functor
 $\Upsilon$
is fully faithful;
$\Upsilon$
is fully faithful;
-
(iii) the triangulated functor
 $\mathsf{D}^{\mathsf{b}}({{\mathsf{Comod}-}} C)\longrightarrow \mathsf{D}^{\mathsf{b}}({{\mathsf{Mod}-}} C^*)$
induced by the comodule inclusion functor
$\mathsf{D}^{\mathsf{b}}({{\mathsf{Comod}-}} C)\longrightarrow \mathsf{D}^{\mathsf{b}}({{\mathsf{Mod}-}} C^*)$
induced by the comodule inclusion functor
 ${{\mathsf{Comod}-}} C\longrightarrow {{\mathsf{Mod}-}} C^*$
is fully faithful;
${{\mathsf{Comod}-}} C\longrightarrow {{\mathsf{Mod}-}} C^*$
is fully faithful;
-
(iv) the triangulated functor
 $\mathsf{D}^+({{\mathsf{Comod}-}} C)\longrightarrow \mathsf{D}^+({{\mathsf{Mod}-}} C^*)$
induced by the comodule inclusion functor is fully faithful;
$\mathsf{D}^+({{\mathsf{Comod}-}} C)\longrightarrow \mathsf{D}^+({{\mathsf{Mod}-}} C^*)$
induced by the comodule inclusion functor is fully faithful;
-
(v) the triangulated functor
 $\Theta ^{\mathsf{b}}:\ \mathsf{D}^{\mathsf{b}}(C{{-\mathsf{Contra}}})\longrightarrow \mathsf{D}^{\mathsf{b}}(C^*{{-\mathsf{Mod}}})$
induced by the contramodule forgetful functor
$\Theta ^{\mathsf{b}}:\ \mathsf{D}^{\mathsf{b}}(C{{-\mathsf{Contra}}})\longrightarrow \mathsf{D}^{\mathsf{b}}(C^*{{-\mathsf{Mod}}})$
induced by the contramodule forgetful functor
 $\Theta :\ C{{-\mathsf{Contra}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
is fully faithful;
$\Theta :\ C{{-\mathsf{Contra}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
is fully faithful;
-
(vi) the triangulated functor
 $\Theta ^-:\ \mathsf{D}^-(C{{-\mathsf{Contra}}})\longrightarrow \mathsf{D}^-(C^*{{-\mathsf{Mod}}})$
induced by the contramodule forgetful functor
$\Theta ^-:\ \mathsf{D}^-(C{{-\mathsf{Contra}}})\longrightarrow \mathsf{D}^-(C^*{{-\mathsf{Mod}}})$
induced by the contramodule forgetful functor
 $\Theta$
is fully faithful;
$\Theta$
is fully faithful;
-
(vii) the
 $k$
-vector space
$k$
-vector space
 $\textrm {Ext}^n_C(k,k)$
is finite-dimensional for all
$\textrm {Ext}^n_C(k,k)$
is finite-dimensional for all
 $n\ge 0$
;
$n\ge 0$
; -
(viii) the
 $k$
-vector space
$k$
-vector space
 $\textrm {Ext}^{C,n}(k,k)$
is finite-dimensional for all
$\textrm {Ext}^{C,n}(k,k)$
is finite-dimensional for all
 $n\ge 0$
.
$n\ge 0$
.
Let us discuss the condition of finite-dimensionality of the Ext spaces
![]() $\textrm {Ext}_C^i(k,k)$
for all
$\textrm {Ext}_C^i(k,k)$
for all
![]() $i\ge 0$
in some detail. One can consider the special case when the coalgebra
$i\ge 0$
in some detail. One can consider the special case when the coalgebra
![]() $C$
is positively graded with finite-dimensional components; so
$C$
is positively graded with finite-dimensional components; so
![]() $C$
is the graded dual coalgebra to a positively graded algebra
$C$
is the graded dual coalgebra to a positively graded algebra
![]() $A=\bigoplus _{m=0}^\infty A_m$
with
$A=\bigoplus _{m=0}^\infty A_m$
with
![]() $\dim A_m\lt \infty$
for all
$\dim A_m\lt \infty$
for all
![]() $m\ge 0$
and
$m\ge 0$
and
![]() $A_0=k$
. Then one has
$A_0=k$
. Then one has
![]() $\textrm {Ext}_C^i(k,k)\simeq \bigoplus _{j=i}^\infty \textrm {Ext}_A^{i,j}(k,k)$
and
$\textrm {Ext}_C^i(k,k)\simeq \bigoplus _{j=i}^\infty \textrm {Ext}_A^{i,j}(k,k)$
and
![]() $\textrm {Ext}_A^i(k,k)\simeq \prod _{j=i}^\infty \textrm {Ext}_A^{i,j}(k,k)$
, where
$\textrm {Ext}_A^i(k,k)\simeq \prod _{j=i}^\infty \textrm {Ext}_A^{i,j}(k,k)$
, where
![]() $i$
is the usual cohomological grading on the Ext spaces, while the internal grading
$i$
is the usual cohomological grading on the Ext spaces, while the internal grading
![]() $j$
is induced by the grading on
$j$
is induced by the grading on
![]() $A$
(cf. [Reference Polishchuk and Positselski17, Section 1 of Chapter 1], [Reference Positselski35, Section 2.1], and [Reference Positselski19, Section 2]).
$A$
(cf. [Reference Polishchuk and Positselski17, Section 1 of Chapter 1], [Reference Positselski35, Section 2.1], and [Reference Positselski19, Section 2]).
Assume further that
![]() $A$
is multiplicatively generated by
$A$
is multiplicatively generated by
![]() $A_1$
with relations of degree
$A_1$
with relations of degree
![]() $2$
; so
$2$
; so
![]() $A$
is a quadratic algebra with finite-dimensional components over
$A$
is a quadratic algebra with finite-dimensional components over
![]() $k$
. Then the vector spaces
$k$
. Then the vector spaces
![]() $\textrm {Ext}_C^i(k,k)$
or
$\textrm {Ext}_C^i(k,k)$
or
![]() $\textrm {Ext}_A^i(k,k)$
still need not be finite-dimensional; in fact,
$\textrm {Ext}_A^i(k,k)$
still need not be finite-dimensional; in fact,
![]() $\textrm {Ext}_C^3(k,k)$
or (equivalently)
$\textrm {Ext}_C^3(k,k)$
or (equivalently)
![]() $\textrm {Ext}_A^3(k,k)$
can be infinite-dimensional already [Reference Anick1, Theorem 7.6], [Reference Fröberg, Gulliksen and Löfwall7], [Reference Polishchuk and Positselski17, Section 6 of Chapter 6].
$\textrm {Ext}_A^3(k,k)$
can be infinite-dimensional already [Reference Anick1, Theorem 7.6], [Reference Fröberg, Gulliksen and Löfwall7], [Reference Polishchuk and Positselski17, Section 6 of Chapter 6].
Nevertheless, for a (homogeneous) Koszul
![]() $k$
-algebra
$k$
-algebra
![]() $A$
with finite-dimensional grading components [Reference Polishchuk and Positselski17, Reference Priddy40] and the graded dual coalgebra
$A$
with finite-dimensional grading components [Reference Polishchuk and Positselski17, Reference Priddy40] and the graded dual coalgebra
![]() $C$
, the vector spaces
$C$
, the vector spaces
![]() $\textrm {Ext}_C^i(k,k)$
and
$\textrm {Ext}_C^i(k,k)$
and
![]() $\textrm {Ext}_A^i(k,k)$
are, of course, finite-dimensional for all
$\textrm {Ext}_A^i(k,k)$
are, of course, finite-dimensional for all
![]() $i\ge 0$
. More generally, for a finitely cogenerated conilpotent coalgebra
$i\ge 0$
. More generally, for a finitely cogenerated conilpotent coalgebra
![]() $C$
, all the vector spaces
$C$
, all the vector spaces
![]() $\textrm {Ext}_C^i(k,k)$
are finite-dimensional whenever the Ext-algebra
$\textrm {Ext}_C^i(k,k)$
are finite-dimensional whenever the Ext-algebra
![]() $\textrm {Ext}_C^*(k,k)$
is generated by
$\textrm {Ext}_C^*(k,k)$
is generated by
![]() $\textrm {Ext}_C^1(k,k)$
. This includes the important particular case when the Ext-algebra
$\textrm {Ext}_C^1(k,k)$
. This includes the important particular case when the Ext-algebra
![]() $\textrm {Ext}_C^*(k,k)$
is Koszul (but the coalgebra
$\textrm {Ext}_C^*(k,k)$
is Koszul (but the coalgebra
![]() $C$
need not be graded) described in [Reference Positselski and Vishik39, Main Theorem] and [Reference Positselski26, Sections 5–6]. Here we keep assuming that the coalgebra
$C$
need not be graded) described in [Reference Positselski and Vishik39, Main Theorem] and [Reference Positselski26, Sections 5–6]. Here we keep assuming that the coalgebra
![]() $C$
is finitely cogenerated.
$C$
is finitely cogenerated.
With these important special cases in mind, we call a conilpotent coalgebra
![]() $C$
weakly finitely Koszul if the vector space
$C$
weakly finitely Koszul if the vector space
![]() $\textrm {Ext}_C^n(k,k)$
is finite-dimensional for every
$\textrm {Ext}_C^n(k,k)$
is finite-dimensional for every
![]() $n\ge 0$
. This terminology goes back to [Reference Positselski35, Sections 5.4 and 5.7].
$n\ge 0$
. This terminology goes back to [Reference Positselski35, Sections 5.4 and 5.7].
Let us emphasize that we do not know whether the induced triangulated functors between the unbounded derived categories
are fully faithful under the equivalent conditions of Theorem1.2 (or even for a graded coalgebra
![]() $C$
graded dual to a Koszul algebra
$C$
graded dual to a Koszul algebra
![]() $A$
with finite-dimensional components) in general. However, the triangulated functors
$A$
with finite-dimensional components) in general. However, the triangulated functors
![]() $\Upsilon ^\varnothing$
and
$\Upsilon ^\varnothing$
and
![]() $\Theta ^\varnothing$
are known to be fully faithful for any finitely cogenerated conilpotent cocommutative coalgebra
$\Theta ^\varnothing$
are known to be fully faithful for any finitely cogenerated conilpotent cocommutative coalgebra
![]() $C$
. This is a particular case of [Reference Positselski25, Theorems 1.3 and 2.9] (applied to the complete Noetherian commutative local
$C$
. This is a particular case of [Reference Positselski25, Theorems 1.3 and 2.9] (applied to the complete Noetherian commutative local
![]() $k$
-algebra
$k$
-algebra
![]() $R=C^*$
with its maximal ideal
$R=C^*$
with its maximal ideal
![]() $I=\mathfrak m$
).
$I=\mathfrak m$
).
In this connection, it should first of all be mentioned that all finitely cogenerated conilpotent cocommutative coalgebras
![]() $C$
are weakly finitely Koszul since they are Artinian, and consequently, co-Noetherian [Reference Positselski29, Section 2]. Quite generally, any left or right co-Noetherian conilpotent coalgebra is weakly finitely Koszul (and so is any finitely cogenerated left or right cocoherent coalgebra). But this does not seem to be enough. The proofs of [Reference Positselski25, Theorems 1.3 and 2.9] are essentially based on the observation that the right adjoint functor
$C$
are weakly finitely Koszul since they are Artinian, and consequently, co-Noetherian [Reference Positselski29, Section 2]. Quite generally, any left or right co-Noetherian conilpotent coalgebra is weakly finitely Koszul (and so is any finitely cogenerated left or right cocoherent coalgebra). But this does not seem to be enough. The proofs of [Reference Positselski25, Theorems 1.3 and 2.9] are essentially based on the observation that the right adjoint functor
![]() $\Gamma$
to
$\Gamma$
to
![]() $\Upsilon$
and the left adjoint functor
$\Upsilon$
and the left adjoint functor
![]() $\Delta$
to
$\Delta$
to
![]() $\Theta$
have finite homological dimensions (cf. [Reference Positselski28, Theorem 6.4] and [Reference Positselski31, Proposition 6.5]). We cannot think of any general noncommutative versions of these properties, proved in [Reference Porta, Shaul and Yekutieli18] and [Reference Positselski25] using commutative Koszul complexes.
$\Theta$
have finite homological dimensions (cf. [Reference Positselski28, Theorem 6.4] and [Reference Positselski31, Proposition 6.5]). We cannot think of any general noncommutative versions of these properties, proved in [Reference Porta, Shaul and Yekutieli18] and [Reference Positselski25] using commutative Koszul complexes.
2. Preliminaries on coalgebras, comodules, and contramodules
Unless otherwise mentioned, all coalgebras, comodules, and contramodules in this paper are presumed to be coassociative and counital; all coalgebra homomorphisms are presumed to preserve the counit. Dually, all rings, algebras, and modules are presumed to be associative and unital.
A (coassociative, counital) coalgebra
![]() $C$
over a field
$C$
over a field
![]() $k$
is a
$k$
is a
![]() $k$
-vector space endowed with
$k$
-vector space endowed with
![]() $k$
-linear maps of comultiplication
$k$
-linear maps of comultiplication
![]() $\mu :\ C\longrightarrow C\otimes _k C$
and counit
$\mu :\ C\longrightarrow C\otimes _k C$
and counit
![]() $\epsilon :\ C\longrightarrow k$
satisfying the usual coassociativity and counitality axioms (which can be obtained by writing down the definition of an associative, unital
$\epsilon :\ C\longrightarrow k$
satisfying the usual coassociativity and counitality axioms (which can be obtained by writing down the definition of an associative, unital
![]() $k$
-algebra in the tensor notation and inverting the arrows). We suggest the books [Reference Montgomery16, Reference Sweedler44] as the standard reference sources on coalgebras over a field. The present author’s surveys [Reference Positselski24, Section 1], [Reference Positselski36, Section 3] can be used as additional reference sources.
$k$
-algebra in the tensor notation and inverting the arrows). We suggest the books [Reference Montgomery16, Reference Sweedler44] as the standard reference sources on coalgebras over a field. The present author’s surveys [Reference Positselski24, Section 1], [Reference Positselski36, Section 3] can be used as additional reference sources.
Let
![]() $C$
be a coalgebra over
$C$
be a coalgebra over
![]() $k$
. A right
$k$
. A right
![]() $C$
-comodule
$C$
-comodule
![]() $N$
is a
$N$
is a
![]() $k$
-vector space endowed with a
$k$
-vector space endowed with a
![]() $k$
-linear map of right coaction
$k$
-linear map of right coaction
![]() $\nu :\ N\longrightarrow N\otimes _k C$
satisfying the usual coassociativity and counitality axioms (which can be obtained by inverting the arrows in the definition of a module over an associative, unital algebra). Similarly, a left
$\nu :\ N\longrightarrow N\otimes _k C$
satisfying the usual coassociativity and counitality axioms (which can be obtained by inverting the arrows in the definition of a module over an associative, unital algebra). Similarly, a left
![]() $C$
-comodule
$C$
-comodule
![]() $M$
is a
$M$
is a
![]() $k$
-vector space endowed with a
$k$
-vector space endowed with a
![]() $k$
-linear map of left coaction
$k$
-linear map of left coaction
![]() $\nu :\ M\longrightarrow C\otimes _k M$
satisfying the coassociativity and counitality axioms.
$\nu :\ M\longrightarrow C\otimes _k M$
satisfying the coassociativity and counitality axioms.
A left
![]() $C$
-contramodule (see [Reference Eilenberg and Moore5, Section III.5], [Reference Positselski20, Sections 0.2.4 and 3.1.1, and Appendix A], [Reference Positselski24, Sections 1.1–1.6], and [Reference Positselski36, Section 8]) is a
$C$
-contramodule (see [Reference Eilenberg and Moore5, Section III.5], [Reference Positselski20, Sections 0.2.4 and 3.1.1, and Appendix A], [Reference Positselski24, Sections 1.1–1.6], and [Reference Positselski36, Section 8]) is a
![]() $k$
-vector space
$k$
-vector space
![]() $P$
endowed with a
$P$
endowed with a
![]() $k$
-linear map of left contraaction
$k$
-linear map of left contraaction
![]() $\pi :\ \textrm {Hom}_k(C,P)\longrightarrow P$
satisfying the following contraassociativity and contraunitality axioms. First, the two maps
$\pi :\ \textrm {Hom}_k(C,P)\longrightarrow P$
satisfying the following contraassociativity and contraunitality axioms. First, the two maps
![]() $\textrm {Hom}(C,\pi )$
and
$\textrm {Hom}(C,\pi )$
and
![]() $\textrm {Hom}(\mu, P)\;:\; \textrm {Hom}_k(C\otimes _kC,\ P)\;\simeq\;\textrm {Hom}_k(C,\textrm {Hom}_k(C,P))\longrightarrow \textrm {Hom}_k(C,P)$
must have equal compositions with the contraaction map
$\textrm {Hom}(\mu, P)\;:\; \textrm {Hom}_k(C\otimes _kC,\ P)\;\simeq\;\textrm {Hom}_k(C,\textrm {Hom}_k(C,P))\longrightarrow \textrm {Hom}_k(C,P)$
must have equal compositions with the contraaction map
![]() $\pi :\ \textrm {Hom}_k(C,P)\longrightarrow P$
,
$\pi :\ \textrm {Hom}_k(C,P)\longrightarrow P$
,
Second, the composition of the map
![]() $\textrm {Hom}(\epsilon, P)\;:\; P\longrightarrow \textrm {Hom}_k(C,P)$
with the map
$\textrm {Hom}(\epsilon, P)\;:\; P\longrightarrow \textrm {Hom}_k(C,P)$
with the map
![]() $\pi :\ \textrm {Hom}_k(C,P)\longrightarrow P$
must be equal to the identity endomorphism of
$\pi :\ \textrm {Hom}_k(C,P)\longrightarrow P$
must be equal to the identity endomorphism of
![]() $P$
,
$P$
,
Here the
![]() $k$
-vector space isomorphism
$k$
-vector space isomorphism
![]() $\textrm {Hom}_k(C\otimes _kC,\ P) \simeq \textrm {Hom}_k(C,\textrm {Hom}_k(C,P))$
is obtained as a particular case of the adjunction isomorphism
$\textrm {Hom}_k(C\otimes _kC,\ P) \simeq \textrm {Hom}_k(C,\textrm {Hom}_k(C,P))$
is obtained as a particular case of the adjunction isomorphism
![]() $\textrm {Hom}_k(U\otimes _kV,\ W)\simeq \textrm {Hom}_k(V,\textrm {Hom}_k(U,W))$
, which holds for any vector spaces
$\textrm {Hom}_k(U\otimes _kV,\ W)\simeq \textrm {Hom}_k(V,\textrm {Hom}_k(U,W))$
, which holds for any vector spaces
![]() $U$
,
$U$
,
![]() $V$
, and
$V$
, and
![]() $W$
.
$W$
.
The definition of a right
![]() $C$
-contramodule is similar, with the only difference that the isomorphism
$C$
-contramodule is similar, with the only difference that the isomorphism
![]() $\textrm {Hom}_k(C\otimes _kC,\ P) \simeq \textrm {Hom}_k(C,\textrm {Hom}_k(C,P))$
arising as a particular case of the identification
$\textrm {Hom}_k(C\otimes _kC,\ P) \simeq \textrm {Hom}_k(C,\textrm {Hom}_k(C,P))$
arising as a particular case of the identification
![]() $\textrm {Hom}_k(V\otimes _kU,\ W)\simeq \textrm {Hom}_k(V,\textrm {Hom}_k(U,W))$
is used.
$\textrm {Hom}_k(V\otimes _kU,\ W)\simeq \textrm {Hom}_k(V,\textrm {Hom}_k(U,W))$
is used.
For any right
![]() $C$
-comodule
$C$
-comodule
![]() $N$
and any
$N$
and any
![]() $k$
-vector space
$k$
-vector space
![]() $V$
, the vector space
$V$
, the vector space
![]() $\textrm {Hom}_k(N,V)$
has a natural left
$\textrm {Hom}_k(N,V)$
has a natural left
![]() $C$
-contramodule structure. The left contraaction map
$C$
-contramodule structure. The left contraaction map
is constructed by applying the functor
![]() $\textrm {Hom}_k({-},V)$
to the right coaction map
$\textrm {Hom}_k({-},V)$
to the right coaction map
![]() $\nu :\ N\longrightarrow N\otimes _kC$
, i. e.,
$\nu :\ N\longrightarrow N\otimes _kC$
, i. e.,
![]() $\pi =\textrm {Hom}_k(\nu, V)$
.
$\pi =\textrm {Hom}_k(\nu, V)$
.
Let
![]() $C^{\mathrm{op}}$
denote the opposite coalgebra to
$C^{\mathrm{op}}$
denote the opposite coalgebra to
![]() $C$
(i. e., the same vector space endowed with the same counit and the left-right opposite comultiplication to that in
$C$
(i. e., the same vector space endowed with the same counit and the left-right opposite comultiplication to that in
![]() $C$
). Similarly, given a ring
$C$
). Similarly, given a ring
![]() $A$
, we denote by
$A$
, we denote by
![]() $A^{\mathrm{op}}$
the opposite ring. Then right
$A^{\mathrm{op}}$
the opposite ring. Then right
![]() $C$
-comodules are the same things as left
$C$
-comodules are the same things as left
![]() $C^{\mathrm{op}}$
-comodules, and vice versa.
$C^{\mathrm{op}}$
-comodules, and vice versa.
We will use the notation
![]() $\textrm {Hom}_C({-},{-})$
for the vector spaces of morphisms in the category of left
$\textrm {Hom}_C({-},{-})$
for the vector spaces of morphisms in the category of left
![]() $C$
-comodules
$C$
-comodules
![]() $C{{-\mathsf{Comod}}}$
and the notation
$C{{-\mathsf{Comod}}}$
and the notation
![]() $\textrm {Hom}_{C^{\mathrm{op}}}({-},{-})$
for the vector spaces of morphisms in the category of right
$\textrm {Hom}_{C^{\mathrm{op}}}({-},{-})$
for the vector spaces of morphisms in the category of right
![]() $C$
-comodules
$C$
-comodules
![]() ${{\mathsf{Comod}-}} C$
. The vector spaces of morphisms in the left and right contramodule categories
${{\mathsf{Comod}-}} C$
. The vector spaces of morphisms in the left and right contramodule categories
![]() $C{{-\mathsf{Contra}}}$
and
$C{{-\mathsf{Contra}}}$
and
![]() ${{\mathsf{Contra-}}} C$
will be denoted by
${{\mathsf{Contra-}}} C$
will be denoted by
![]() $\textrm {Hom}^C({-},{-})$
and
$\textrm {Hom}^C({-},{-})$
and
![]() $\textrm {Hom}^{C^{\mathrm{op}}}({-},{-})$
. Similarly, the Yoneda Ext spaces are denoted by
$\textrm {Hom}^{C^{\mathrm{op}}}({-},{-})$
. Similarly, the Yoneda Ext spaces are denoted by
![]() $\textrm {Ext}_C^*({-},{-})$
in
$\textrm {Ext}_C^*({-},{-})$
in
![]() $C{{-\mathsf{Comod}}}$
, by
$C{{-\mathsf{Comod}}}$
, by
![]() $\textrm {Ext}_{C^{\mathrm{op}}}^*({-},{-})$
in
$\textrm {Ext}_{C^{\mathrm{op}}}^*({-},{-})$
in
![]() ${{\mathsf{Comod}-}} C$
, and by
${{\mathsf{Comod}-}} C$
, and by
![]() $\textrm {Ext}^{C,*}({-},{-})$
in
$\textrm {Ext}^{C,*}({-},{-})$
in
![]() $C{{-\mathsf{Contra}}}$
.
$C{{-\mathsf{Contra}}}$
.
The category of left
![]() $C$
-comodules
$C$
-comodules
![]() $C{{-\mathsf{Comod}}}$
is a locally finite Grothendieck abelian category. Any
$C{{-\mathsf{Comod}}}$
is a locally finite Grothendieck abelian category. Any
![]() $C$
-comodule is the union of its finite-dimensional subcomodules [Reference Sweedler44, Propositions 2.1.1–2.1.2 and Corollary 2.1.4], [Reference Positselski36, Lemma 3.1(b)]. The forgetful functor
$C$
-comodule is the union of its finite-dimensional subcomodules [Reference Sweedler44, Propositions 2.1.1–2.1.2 and Corollary 2.1.4], [Reference Positselski36, Lemma 3.1(b)]. The forgetful functor
![]() $C{{-\mathsf{Comod}}}\longrightarrow k{{-\mathsf{Vect}}}$
from the category of
$C{{-\mathsf{Comod}}}\longrightarrow k{{-\mathsf{Vect}}}$
from the category of
![]() $C$
-comodules to the category of
$C$
-comodules to the category of
![]() $k$
-vector spaces is exact and preserves the infinite coproducts (but not the infinite products). So the coproduct (and more generally, filtered direct limit) functors are exact in
$k$
-vector spaces is exact and preserves the infinite coproducts (but not the infinite products). So the coproduct (and more generally, filtered direct limit) functors are exact in
![]() $C{{-\mathsf{Comod}}}$
, while the functors of infinite product are usually not exact.
$C{{-\mathsf{Comod}}}$
, while the functors of infinite product are usually not exact.
Left
![]() $C$
-comodules of the form
$C$
-comodules of the form
![]() $C\otimes _k V$
and right
$C\otimes _k V$
and right
![]() $C$
-comodules of the form
$C$
-comodules of the form
![]() $V\otimes _k C$
, where
$V\otimes _k C$
, where
![]() $V$
ranges over the
$V$
ranges over the
![]() $k$
-vector spaces, are called the cofree
$k$
-vector spaces, are called the cofree
![]() $C$
-comodules. For any left
$C$
-comodules. For any left
![]() $C$
-comodule
$C$
-comodule
![]() $L$
, the vector space of
$L$
, the vector space of
![]() $C$
-comodule morphisms
$C$
-comodule morphisms
![]() $L\longrightarrow C\otimes _k V$
is naturally isomorphic to the vector space of
$L\longrightarrow C\otimes _k V$
is naturally isomorphic to the vector space of
![]() $k$
-linear maps
$k$
-linear maps
![]() $L\longrightarrow V$
,
$L\longrightarrow V$
,
Hence, the cofree comodules are injective (as objects of
![]() $C{{-\mathsf{Comod}}}$
or
$C{{-\mathsf{Comod}}}$
or
![]() ${{\mathsf{Comod}-}} C$
). A
${{\mathsf{Comod}-}} C$
). A
![]() $C$
-comodule is injective if and only if it is a direct summand of a cofree one.
$C$
-comodule is injective if and only if it is a direct summand of a cofree one.
The category of left
![]() $C$
-contramodules
$C$
-contramodules
![]() $C{{-\mathsf{Contra}}}$
is a locally presentable abelian category with enough projective objects. The forgetful functor
$C{{-\mathsf{Contra}}}$
is a locally presentable abelian category with enough projective objects. The forgetful functor
![]() $C{{-\mathsf{Contra}}}\longrightarrow k{{-\mathsf{Vect}}}$
is exact and preserves the infinite products (but not the infinite coproducts). Hence, the functors of infinite product are exact in
$C{{-\mathsf{Contra}}}\longrightarrow k{{-\mathsf{Vect}}}$
is exact and preserves the infinite products (but not the infinite coproducts). Hence, the functors of infinite product are exact in
![]() $C{{-\mathsf{Contra}}}$
, while the coproduct functors are usually not exact.
$C{{-\mathsf{Contra}}}$
, while the coproduct functors are usually not exact.
Left
![]() $C$
-contramodules of the form
$C$
-contramodules of the form
![]() $\textrm {Hom}_k(C,V)$
, where
$\textrm {Hom}_k(C,V)$
, where
![]() $V\in k{{-\mathsf{Vect}}}$
, are called the free
$V\in k{{-\mathsf{Vect}}}$
, are called the free
![]() $C$
-contramodules. For any left
$C$
-contramodules. For any left
![]() $C$
-contramodule
$C$
-contramodule
![]() $Q$
, the vector space of
$Q$
, the vector space of
![]() $C$
-contramodule morphisms
$C$
-contramodule morphisms
![]() $\textrm {Hom}_k(C,V)\longrightarrow Q$
is naturally isomorphic to the vector space of
$\textrm {Hom}_k(C,V)\longrightarrow Q$
is naturally isomorphic to the vector space of
![]() $k$
-linear maps
$k$
-linear maps
![]() $V\longrightarrow Q$
,
$V\longrightarrow Q$
,
Hence, the free contramodules are projective (as objects of
![]() $C{{-\mathsf{Contra}}}$
). A
$C{{-\mathsf{Contra}}}$
). A
![]() $C$
-contramodule is projective if and only if it is a direct summand of a free one.
$C$
-contramodule is projective if and only if it is a direct summand of a free one.
Let us introduce a simplified version of the Sweedler notation [Reference Sweedler44, Section 1.2], [Reference Montgomery16, Notation 1.4.2] for the comultiplication in
![]() $C$
. Given an element
$C$
. Given an element
![]() $c\in C$
, we write
$c\in C$
, we write
Following the convention in [Reference Positselski20, Reference Positselski24, Reference Positselski36] (which is opposite to the convention in [Reference Montgomery16, Reference Sweedler44]), we define the associative algebra structure on the dual vector space
![]() $C^*=\textrm {Hom}_k(C,k)$
to a coalgebra
$C^*=\textrm {Hom}_k(C,k)$
to a coalgebra
![]() $C$
by the formula
$C$
by the formula
The counit on
![]() $C$
induces a unit in
$C$
induces a unit in
![]() $C^*$
in the obvious way.
$C^*$
in the obvious way.
Then, for any left
![]() $C$
-comodule
$C$
-comodule
![]() $M$
, the composition
$M$
, the composition
of the map induced by the coaction map
![]() $\nu :\ M\longrightarrow C\otimes _k M$
and the map induced by the pairing map
$\nu :\ M\longrightarrow C\otimes _k M$
and the map induced by the pairing map
![]() $C^*\otimes _k C\longrightarrow k$
endows
$C^*\otimes _k C\longrightarrow k$
endows
![]() $M$
with a left
$M$
with a left
![]() $C^*$
-module structure. Similarly, for any right
$C^*$
-module structure. Similarly, for any right
![]() $C$
-comodule
$C$
-comodule
![]() $N$
, the composition
$N$
, the composition
endows
![]() $N$
with a right
$N$
with a right
![]() $C^*$
-module structure. Finally, for any left
$C^*$
-module structure. Finally, for any left
![]() $C$
-contramodule
$C$
-contramodule
![]() $P$
, the composition
$P$
, the composition
of the natural embedding of vector spaces
![]() $C^*\otimes _k P\rightarrowtail \textrm {Hom}_k(C,P)$
and the contraaction map
$C^*\otimes _k P\rightarrowtail \textrm {Hom}_k(C,P)$
and the contraaction map
![]() $\pi :\ \textrm {Hom}_k(C,P)\longrightarrow P$
endows
$\pi :\ \textrm {Hom}_k(C,P)\longrightarrow P$
endows
![]() $P$
with a left
$P$
with a left
![]() $C^*$
-module structure.
$C^*$
-module structure.
We have constructed the comodule inclusion functors
and the contramodule forgetful functor
The comodule inclusion functors (for a coalgebra
![]() $C$
over a field
$C$
over a field
![]() $k$
) are always fully faithful (see [Reference Sweedler44, Propositions 2.1.1–2.1.2 and Theorem 2.1.3(e)] for a discussion). The contramodule forgetful functor is not fully faithful in general, as we will see in Example 8.2 below.
$k$
) are always fully faithful (see [Reference Sweedler44, Propositions 2.1.1–2.1.2 and Theorem 2.1.3(e)] for a discussion). The contramodule forgetful functor is not fully faithful in general, as we will see in Example 8.2 below.
3. Conilpotent coalgebras and minimal resolutions
What we call conilpotent coalgebras (in the terminology going back to [Reference Positselski and Vishik39, Section 3.1], [Reference Positselski19, Section 4.1]) were called “pointed irreducible” coalgebras in [Reference Sweedler44, Section 8.0]. We refer to [Reference Positselski36, Sections 3.3–3.4] for an introductory discussion.
Let
![]() $D$
be a coalgebra without counit over a field
$D$
be a coalgebra without counit over a field
![]() $k$
. For every
$k$
. For every
![]() $n\ge 1$
, there is the uniquely defined iterated comultiplication map
$n\ge 1$
, there is the uniquely defined iterated comultiplication map
![]() $\mu ^{(n)}:\ D\longrightarrow D^{\otimes n+1}$
. The coalgebra
$\mu ^{(n)}:\ D\longrightarrow D^{\otimes n+1}$
. The coalgebra
![]() $D$
is said to be conilpotent if for every
$D$
is said to be conilpotent if for every
![]() $d\in D$
there exists
$d\in D$
there exists
![]() $n\ge 1$
such that
$n\ge 1$
such that
![]() $\mu ^{(n)}(d)=0$
in
$\mu ^{(n)}(d)=0$
in
![]() $D^{\otimes n+1}$
. Clearly, one then also has
$D^{\otimes n+1}$
. Clearly, one then also has
![]() $\mu ^{(m)}(d)=0$
for all
$\mu ^{(m)}(d)=0$
for all
![]() $m\ge n$
.
$m\ge n$
.
A coaugmentation
![]() $\gamma$
of a coalgebra
$\gamma$
of a coalgebra
![]() $C$
is a homomorphism of (counital) coalgebras
$C$
is a homomorphism of (counital) coalgebras
![]() $\gamma :\ k\longrightarrow C$
. So the composition
$\gamma :\ k\longrightarrow C$
. So the composition
![]() $\epsilon \gamma :\ k\longrightarrow C\longrightarrow k$
must be the identity map.
$\epsilon \gamma :\ k\longrightarrow C\longrightarrow k$
must be the identity map.
Given a coaugmented coalgebra
![]() $(C,\gamma )$
, the cokernel
$(C,\gamma )$
, the cokernel
![]() $D=C/\gamma (k)$
of the map
$D=C/\gamma (k)$
of the map
![]() $\gamma$
has a unique coalgebra structure for which the natural surjection
$\gamma$
has a unique coalgebra structure for which the natural surjection
![]() $C\longrightarrow D$
is a homomorphism of noncounital coalgebras. A coaugmented coalgebra
$C\longrightarrow D$
is a homomorphism of noncounital coalgebras. A coaugmented coalgebra
![]() $C$
us called conilpotent if the noncounital coalgebra
$C$
us called conilpotent if the noncounital coalgebra
![]() $D$
is conilpotent (in the sense of the definition above).
$D$
is conilpotent (in the sense of the definition above).
Obviously, no nonzero noncounital coalgebra homomorphisms
![]() $k\longrightarrow D$
exist for a conilpotent noncounital coalgebra
$k\longrightarrow D$
exist for a conilpotent noncounital coalgebra
![]() $D$
. Consequently, a conilpotent coaugmented coalgebra
$D$
. Consequently, a conilpotent coaugmented coalgebra
![]() $(C,\gamma )$
admits no other coaugmentation but
$(C,\gamma )$
admits no other coaugmentation but
![]() $\gamma$
.
$\gamma$
.
The following result is a version of Nakayama lemma for conilpotent noncounital coalgebras.
Lemma 3.1. (a) Let
![]() $D$
be a conilpotent noncounital coalgebra and
$D$
be a conilpotent noncounital coalgebra and
![]() $M\ne 0$
be a noncounital left
$M\ne 0$
be a noncounital left
![]() $D$
-comodule. Then the coaction map
$D$
-comodule. Then the coaction map
![]() $M\longrightarrow D\otimes _kM$
is not injective.
$M\longrightarrow D\otimes _kM$
is not injective.
(b) Let
![]() $D$
be a conilpotent noncounital coalgebra and
$D$
be a conilpotent noncounital coalgebra and
![]() $P\ne 0$
be a noncounital left
$P\ne 0$
be a noncounital left
![]() $D$
-contramodule. Then the contraaction map
$D$
-contramodule. Then the contraaction map
![]() $\textrm {Hom}_k(D,P)\longrightarrow P$
is not surjective.
$\textrm {Hom}_k(D,P)\longrightarrow P$
is not surjective.
Proof.
Part (a): for the sake of contradiction, assume that the coaction map
![]() $\nu :\ M\longrightarrow D\otimes _kM$
is injective. Then the iterated coaction map
$\nu :\ M\longrightarrow D\otimes _kM$
is injective. Then the iterated coaction map
![]() $\nu ^{(n)}:\ M\longrightarrow D^{\otimes n}\otimes _kM$
is also injective for every
$\nu ^{(n)}:\ M\longrightarrow D^{\otimes n}\otimes _kM$
is also injective for every
![]() $n\ge 1$
.
$n\ge 1$
.
Pick a nonzero element
![]() $x\in M$
, and write
$x\in M$
, and write
![]() $\nu (x)= \sum _{i=1}^r d_r\otimes y_r$
for some
$\nu (x)= \sum _{i=1}^r d_r\otimes y_r$
for some
![]() $d_i\in D$
and
$d_i\in D$
and
![]() $y_i\in M$
. Choose
$y_i\in M$
. Choose
![]() $n\ge 1$
such that
$n\ge 1$
such that
![]() $\mu ^{(n)}(d_i)=0$
in
$\mu ^{(n)}(d_i)=0$
in
![]() $D^{\otimes n+1}$
for every
$D^{\otimes n+1}$
for every
![]() $1\le i\le r$
. Then
$1\le i\le r$
. Then
![]() $\nu ^{(n+1)}(x)=\sum _{i=1}^r\mu ^{(n)}(d_i)\otimes y_i=0$
in
$\nu ^{(n+1)}(x)=\sum _{i=1}^r\mu ^{(n)}(d_i)\otimes y_i=0$
in
![]() $D^{\otimes n+1}\otimes _k M$
, a contradiction.
$D^{\otimes n+1}\otimes _k M$
, a contradiction.
The proof of part (b) is a bit more involved; it can be found in [Reference Positselski20, Lemma A.2.1]. For a discussion of generalizations and other versions of the comodule and contramodule Nakayama lemmas, see [Reference Positselski24, Lemma 2.1].
Let
![]() $E$
be a subcoalgebra in a coalgebra
$E$
be a subcoalgebra in a coalgebra
![]() $C$
. Then in any left
$C$
. Then in any left
![]() $C$
-comodule
$C$
-comodule
![]() $M$
there exists a unique maximal subcomodule whose
$M$
there exists a unique maximal subcomodule whose
![]() $C$
-comodule structure arises from an
$C$
-comodule structure arises from an
![]() $E$
-comodule structure. We denote this subcomodule, which can be computed as the kernel of the composition of maps
$E$
-comodule structure. We denote this subcomodule, which can be computed as the kernel of the composition of maps
![]() $M\longrightarrow C\otimes _k M\longrightarrow C/E\otimes _kM$
, by
$M\longrightarrow C\otimes _k M\longrightarrow C/E\otimes _kM$
, by
![]() ${}_EM\subset M$
. The similar subcomodule of a right
${}_EM\subset M$
. The similar subcomodule of a right
![]() $C$
-comodule
$C$
-comodule
![]() $N$
will be denoted by
$N$
will be denoted by
![]() $N_E\subset N$
.
$N_E\subset N$
.
Dually, any left
![]() $C$
-contramodule
$C$
-contramodule
![]() $P$
admits a unique maximal quotient contramodule whose
$P$
admits a unique maximal quotient contramodule whose
![]() $C$
-contramodule structure arises from an
$C$
-contramodule structure arises from an
![]() $E$
-contramodule structure. We denote this quotient contramodule, which can be computed as the cokernel of the composition of maps
$E$
-contramodule structure. We denote this quotient contramodule, which can be computed as the cokernel of the composition of maps
![]() $\textrm {Hom}_k(C/E,P)\longrightarrow \textrm {Hom}_k(C,P)\longrightarrow P$
, by
$\textrm {Hom}_k(C/E,P)\longrightarrow \textrm {Hom}_k(C,P)\longrightarrow P$
, by
![]() ${}^E\!P\twoheadleftarrow P$
. A further discussion of the functors
${}^E\!P\twoheadleftarrow P$
. A further discussion of the functors
![]() $M\longmapsto {}_EM$
and
$M\longmapsto {}_EM$
and
![]() $P\longmapsto {}^E\!P$
can be found in [Reference Positselski29, Section 2] or [Reference Positselski36, Section 8.4].
$P\longmapsto {}^E\!P$
can be found in [Reference Positselski29, Section 2] or [Reference Positselski36, Section 8.4].
For any right
![]() $C$
-comodule
$C$
-comodule
![]() $N$
, any subcoalgebra
$N$
, any subcoalgebra
![]() $E\subset C$
, and any
$E\subset C$
, and any
![]() $k$
-vector space
$k$
-vector space
![]() $V$
, there is a natural isomorphism of left
$V$
, there is a natural isomorphism of left
![]() $E$
-contramodules
$E$
-contramodules
where the left contramodule structure on the space of linear maps from a right comodule to a vector space is constructed as explained in Section 2. The natural isomorphism (4) follows immediately from the constructions of the functors
![]() $M\longmapsto {}_EM$
and
$M\longmapsto {}_EM$
and
![]() $P\longmapsto {}^E\!P$
above.
$P\longmapsto {}^E\!P$
above.
In this section, we will be interested in the particular case when
![]() $(C,\gamma )$
is a coaugmented (eventually, conilpotent) coalgebra and
$(C,\gamma )$
is a coaugmented (eventually, conilpotent) coalgebra and
![]() $E=\gamma (k)\subset C$
. In this case, we put
$E=\gamma (k)\subset C$
. In this case, we put
![]() ${}_\gamma M={}_EM$
and
${}_\gamma M={}_EM$
and
![]() ${}^\gamma \!P={}^E\!P$
. The similar notation for a right
${}^\gamma \!P={}^E\!P$
. The similar notation for a right
![]() $C$
-comodule
$C$
-comodule
![]() $N$
is
$N$
is
![]() $N_\gamma =N_E$
, and for a right
$N_\gamma =N_E$
, and for a right
![]() $C$
-contramodule
$C$
-contramodule
![]() $Q$
it is
$Q$
it is
![]() $Q^\gamma =Q^E$
. Endowing the one-dimensional
$Q^\gamma =Q^E$
. Endowing the one-dimensional
![]() $k$
-vector space
$k$
-vector space
![]() $k$
with the (left and right)
$k$
with the (left and right)
![]() $C$
-comodule and
$C$
-comodule and
![]() $C$
-contramodule structures defined in terms of
$C$
-contramodule structures defined in terms of
![]() $\gamma$
, one has natural isomorphisms of
$\gamma$
, one has natural isomorphisms of
![]() $k$
-vector spaces
$k$
-vector spaces
One can further compute the vector space
![]() ${}^\gamma \!P$
as the contratensor product
${}^\gamma \!P$
as the contratensor product
![]() $k\odot _CP$
(see [Reference Positselski24, Section 3.1] for the definition), but we will not need to use this fact.
$k\odot _CP$
(see [Reference Positselski24, Section 3.1] for the definition), but we will not need to use this fact.
Lemma 3.2. (a) Let
![]() $(C,\gamma )$
be a conilpotent coaugmented coalgebra and
$(C,\gamma )$
be a conilpotent coaugmented coalgebra and
![]() $M\ne 0$
be a left
$M\ne 0$
be a left
![]() $C$
-comodule. Then
$C$
-comodule. Then
![]() ${}_\gamma M\ne 0$
.
${}_\gamma M\ne 0$
.
(b) Let
![]() $(C,\gamma )$
be a conilpotent coaugmented coalgebra and
$(C,\gamma )$
be a conilpotent coaugmented coalgebra and
![]() $P\ne 0$
be a left
$P\ne 0$
be a left
![]() $C$
-contramodule. Then
$C$
-contramodule. Then
![]() ${}^\gamma \!P\ne 0$
.
${}^\gamma \!P\ne 0$
.
Proof.
This is an equivalent restatement of Lemma 3.1 for
![]() $D=C/\gamma (k)$
.
$D=C/\gamma (k)$
.
For a conilpotent coalgebra
![]() $C$
, the subcomodule
$C$
, the subcomodule
![]() ${}_\gamma M$
of a
${}_\gamma M$
of a
![]() $C$
-comodule
$C$
-comodule
![]() $M$
can be also described as the socle (i.e., the maximal semisimple subcomodule) of
$M$
can be also described as the socle (i.e., the maximal semisimple subcomodule) of
![]() $M$
, and the quotient contramodule
$M$
, and the quotient contramodule
![]() ${}^\gamma \!P$
of a
${}^\gamma \!P$
of a
![]() $C$
-contramodule
$C$
-contramodule
![]() $P$
can be described as the cosocle (i.e., the maximal semisimple quotient contramodule) of
$P$
can be described as the cosocle (i.e., the maximal semisimple quotient contramodule) of
![]() $P$
.
$P$
.
Lemma 3.3.
Let
![]() $(C,\gamma )$
be a conilpotent coaugmented coalgebra. Then
$(C,\gamma )$
be a conilpotent coaugmented coalgebra. Then
(a) a morphism of left
![]() $C$
-comodules
$C$
-comodules
![]() $f:\ L\longrightarrow M$
is injective if and only if the induced map of vector spaces
$f:\ L\longrightarrow M$
is injective if and only if the induced map of vector spaces
![]() ${}_\gamma f:\ {}_\gamma L\longrightarrow {}_\gamma M$
is injective;
${}_\gamma f:\ {}_\gamma L\longrightarrow {}_\gamma M$
is injective;
(b) a morphism of left
![]() $C$
-contramodules
$C$
-contramodules
![]() $f:\ P\longrightarrow Q$
is surjective if and only if the induced map of vector spaces
$f:\ P\longrightarrow Q$
is surjective if and only if the induced map of vector spaces
![]() ${}^\gamma \!f:\ {}^\gamma \!P\longrightarrow {}^\gamma Q$
is surjective.
${}^\gamma \!f:\ {}^\gamma \!P\longrightarrow {}^\gamma Q$
is surjective.
Proof.
Part (a): if the map
![]() $f$
is injective, then so is the map
$f$
is injective, then so is the map
![]() ${}_\gamma f$
since
${}_\gamma f$
since
![]() ${}_\gamma N$
is a vector subspace in
${}_\gamma N$
is a vector subspace in
![]() $N$
for every left
$N$
for every left
![]() $C$
-comodule
$C$
-comodule
![]() $N$
. Conversely, the functor
$N$
. Conversely, the functor
![]() $N\longmapsto {}_\gamma N$
is left exact; so if
$N\longmapsto {}_\gamma N$
is left exact; so if
![]() $K=\ker (f)\in C{{-\mathsf{Comod}}}$
, then
$K=\ker (f)\in C{{-\mathsf{Comod}}}$
, then
![]() ${}_\gamma K=\ker ({}_\gamma f)$
. Now if
${}_\gamma K=\ker ({}_\gamma f)$
. Now if
![]() ${}_\gamma K=0$
, then
${}_\gamma K=0$
, then
![]() $K=0$
by Lemma 3.2(a). The proof of part (b) is similar (or rather, dual-analogous in the sense of [Reference Positselski36, Section 8.2]). The functor
$K=0$
by Lemma 3.2(a). The proof of part (b) is similar (or rather, dual-analogous in the sense of [Reference Positselski36, Section 8.2]). The functor
![]() $P\longmapsto {}^\gamma \!P$
is right exact, etc.
$P\longmapsto {}^\gamma \!P$
is right exact, etc.
Lemma 3.4.
Let
![]() $(C,\gamma )$
be a conilpotent coaugmented coalgebra. Then
$(C,\gamma )$
be a conilpotent coaugmented coalgebra. Then
(a) a morphism of injective left
![]() $C$
-comodules
$C$
-comodules
![]() $f:\ I\longrightarrow J$
is an isomorphism if and only if the induced map of vector spaces
$f:\ I\longrightarrow J$
is an isomorphism if and only if the induced map of vector spaces
![]() ${}_\gamma f:\ {}_\gamma I\longrightarrow {}_\gamma J$
is an isomorphism;
${}_\gamma f:\ {}_\gamma I\longrightarrow {}_\gamma J$
is an isomorphism;
(b) a morphism of projective left
![]() $C$
-contramodules
$C$
-contramodules
![]() $f:\ P\longrightarrow Q$
is an isomorphism if and only if the induced map of vector spaces
$f:\ P\longrightarrow Q$
is an isomorphism if and only if the induced map of vector spaces
![]() ${}^\gamma \!f:\ {}^\gamma \!P\longrightarrow {}^\gamma Q$
is an isomorphism.
${}^\gamma \!f:\ {}^\gamma \!P\longrightarrow {}^\gamma Q$
is an isomorphism.
Proof.
Part (a): if the map
![]() ${}_\gamma f$
is injective, then the morphism
${}_\gamma f$
is injective, then the morphism
![]() $f$
is injective by Lemma 3.3(a). Now if the
$f$
is injective by Lemma 3.3(a). Now if the
![]() $C$
-comodule
$C$
-comodule
![]() $I$
is injective, then
$I$
is injective, then
![]() $f$
is a split monomorphism in
$f$
is a split monomorphism in
![]() $C{{-\mathsf{Comod}}}$
. Therefore,
$C{{-\mathsf{Comod}}}$
. Therefore,
![]() ${}_\gamma \textrm {coker}(f)=\textrm {coker}({}_\gamma f)$
and Lemma 3.2(a) tell us that
${}_\gamma \textrm {coker}(f)=\textrm {coker}({}_\gamma f)$
and Lemma 3.2(a) tell us that
![]() $f$
is an isomorphism whenever
$f$
is an isomorphism whenever
![]() ${}_\gamma f$
is. The proof of part (b) is dual-analogous.
${}_\gamma f$
is. The proof of part (b) is dual-analogous.
Lemma 3.5.
Let
![]() $(C,\gamma )$
be a conilpotent coaugmented coalgebra. Then
$(C,\gamma )$
be a conilpotent coaugmented coalgebra. Then
(a) for any left
![]() $C$
-comodule
$C$
-comodule
![]() $M$
there exists a cofree left
$M$
there exists a cofree left
![]() $C$
-comodule
$C$
-comodule
![]() $J$
together with an injective
$J$
together with an injective
![]() $C$
-comodule morphism
$C$
-comodule morphism
![]() $f:\ M\longrightarrow J$
such that the induced map
$f:\ M\longrightarrow J$
such that the induced map
![]() ${}_\gamma f:\ {}_\gamma M \longrightarrow {}_\gamma J$
is an isomorphism of
${}_\gamma f:\ {}_\gamma M \longrightarrow {}_\gamma J$
is an isomorphism of
![]() $k$
-vector spaces;
$k$
-vector spaces;
(b) for any left
![]() $C$
-contramodule
$C$
-contramodule
![]() $Q$
there exists a free left
$Q$
there exists a free left
![]() $C$
-contramodule
$C$
-contramodule
![]() $P$
together with a surjective
$P$
together with a surjective
![]() $C$
-contramodule morphism
$C$
-contramodule morphism
![]() $f:\ P\longrightarrow Q$
such that the induced map
$f:\ P\longrightarrow Q$
such that the induced map
![]() ${}^\gamma \!f:\ {}^\gamma \!P\longrightarrow {}^\gamma Q$
is an isomorphism of
${}^\gamma \!f:\ {}^\gamma \!P\longrightarrow {}^\gamma Q$
is an isomorphism of
![]() $k$
-vector spaces.
$k$
-vector spaces.
Proof.
Part (a): put
![]() $V={}_\gamma M$
and
$V={}_\gamma M$
and
![]() $J=C\otimes _k V$
. Then the injective map
$J=C\otimes _k V$
. Then the injective map
![]() $V\longrightarrow J$
induced by the map
$V\longrightarrow J$
induced by the map
![]() $\gamma :\ k \longrightarrow C$
is a
$\gamma :\ k \longrightarrow C$
is a
![]() $C$
-comodule morphism
$C$
-comodule morphism
![]() $M\supset {}_\gamma M\longrightarrow J$
. Since the cofree comodules are injective, this morphism can be extended to a
$M\supset {}_\gamma M\longrightarrow J$
. Since the cofree comodules are injective, this morphism can be extended to a
![]() $C$
-comodule morphism
$C$
-comodule morphism
![]() $f:\ M\longrightarrow J$
. The morphism
$f:\ M\longrightarrow J$
. The morphism
![]() $f$
is injective by Lemma 3.3(a). The comodule
$f$
is injective by Lemma 3.3(a). The comodule
![]() $J$
can be also described as an injective envelope of the comodule
$J$
can be also described as an injective envelope of the comodule
![]() $M$
in the comodule category
$M$
in the comodule category
![]() $C{{-\mathsf{Comod}}}$
. The proof of part (b) is dual analogous; the contramodule
$C{{-\mathsf{Comod}}}$
. The proof of part (b) is dual analogous; the contramodule
![]() $P$
can be also described as a projective cover of the contramodule
$P$
can be also described as a projective cover of the contramodule
![]() $Q$
in contramodule category
$Q$
in contramodule category
![]() $C{{-\mathsf{Contra}}}$
(cf. [Reference Positselski32, Example 12.3]).
$C{{-\mathsf{Contra}}}$
(cf. [Reference Positselski32, Example 12.3]).
Corollary 3.6.
Let
![]() $C$
be a conilpotent (coaugmented) coalgebra. Then
$C$
be a conilpotent (coaugmented) coalgebra. Then
(a) a
![]() $C$
-comodule is injective if and only if is cofree;
$C$
-comodule is injective if and only if is cofree;
(b) a
![]() $C$
-contramodule is projective if and only if it is free.
$C$
-contramodule is projective if and only if it is free.
Proof.
Generally speaking, over a coalgebra
![]() $C$
over a field
$C$
over a field
![]() $k$
, the injective comodules are the direct summands of the cofree ones, and the projective contramodules are the direct summands of the free ones (see Section 2). In the situation at hand with a conilpotent coalgebra
$k$
, the injective comodules are the direct summands of the cofree ones, and the projective contramodules are the direct summands of the free ones (see Section 2). In the situation at hand with a conilpotent coalgebra
![]() $C$
, the assersion of part (a) follows straighforwardly from Lemmas 3.4(a) and 3.5(a). Part (b) follows from Lemmas 3.4(b) and 3.5(b).
$C$
, the assersion of part (a) follows straighforwardly from Lemmas 3.4(a) and 3.5(a). Part (b) follows from Lemmas 3.4(b) and 3.5(b).
Let
![]() $K^\bullet$
be a complex of left
$K^\bullet$
be a complex of left
![]() $C$
-comodules. We will say that the complex
$C$
-comodules. We will say that the complex
![]() $K^\bullet$
is minimal if the differential in the complex of vector spaces
$K^\bullet$
is minimal if the differential in the complex of vector spaces
![]() ${}_\gamma K^\bullet$
vanishes. Similarly, a complex of left
${}_\gamma K^\bullet$
vanishes. Similarly, a complex of left
![]() $C$
-contramodules
$C$
-contramodules
![]() $Q_\bullet$
is said to be minimal if the differential in the complex of vector spaces
$Q_\bullet$
is said to be minimal if the differential in the complex of vector spaces
![]() ${}^\gamma Q_\bullet$
vanishes.
${}^\gamma Q_\bullet$
vanishes.
Let
![]() $M$
be a
$M$
be a
![]() $C$
-comodule. An injective coresolution
$C$
-comodule. An injective coresolution
![]() $M\longrightarrow J^\bullet$
of the comodule
$M\longrightarrow J^\bullet$
of the comodule
![]() $M$
is said to be minimal if the complex of comodules
$M$
is said to be minimal if the complex of comodules
![]() $J^\bullet$
is minimal. Dually, a projective resolution
$J^\bullet$
is minimal. Dually, a projective resolution
![]() $Q_\bullet \longrightarrow P$
of a
$Q_\bullet \longrightarrow P$
of a
![]() $C$
-contramodule
$C$
-contramodule
![]() $P$
is said to be minimal if the complex of contramodules
$P$
is said to be minimal if the complex of contramodules
![]() $Q_\bullet$
is minimal.
$Q_\bullet$
is minimal.
Proposition 3.7.
The following assertions hold for any conilpotent coalgebra
![]() $C$
.
$C$
.
(a) Any
![]() $C$
-comodule
$C$
-comodule
![]() $M$
admits a minimal injective coresolution. A minimal injective coresolution of
$M$
admits a minimal injective coresolution. A minimal injective coresolution of
![]() $M$
is unique up to a (nonunique) isomorphism.
$M$
is unique up to a (nonunique) isomorphism.
(b) Any
![]() $C$
-contramodule
$C$
-contramodule
![]() $P$
admits a minimal projective resolution. A minimal projective resolution of
$P$
admits a minimal projective resolution. A minimal projective resolution of
![]() $P$
is unique up to a (nonunique) isomorphism.
$P$
is unique up to a (nonunique) isomorphism.
Proof.
Part (a): to construct a minimal injective coresolution of
![]() $M$
, all one needs to do is to iterate the construction of Lemma 3.5(a). Pick an injective
$M$
, all one needs to do is to iterate the construction of Lemma 3.5(a). Pick an injective
![]() $C$
-comodule
$C$
-comodule
![]() $J^0$
together with an injective morphism of
$J^0$
together with an injective morphism of
![]() $C$
-comodules
$C$
-comodules
![]() $M\longrightarrow J^0$
such that the induced map
$M\longrightarrow J^0$
such that the induced map
![]() ${}_\gamma M\longrightarrow {}_\gamma J^0$
is an isomorphism. Then the induced map
${}_\gamma M\longrightarrow {}_\gamma J^0$
is an isomorphism. Then the induced map
![]() ${}_\gamma J^0\longrightarrow {}_\gamma (J^0/M)$
is zero. Pick an injective
${}_\gamma J^0\longrightarrow {}_\gamma (J^0/M)$
is zero. Pick an injective
![]() $C$
-comodule
$C$
-comodule
![]() $J^1$
together with an injective morphism of
$J^1$
together with an injective morphism of
![]() $C$
-comodules
$C$
-comodules
![]() $J^0/M\longrightarrow J^1$
such that the induced map
$J^0/M\longrightarrow J^1$
such that the induced map
![]() ${}_\gamma (J^0/M)\longrightarrow {}_\gamma J^1$
is an isomorphism, etc.
${}_\gamma (J^0/M)\longrightarrow {}_\gamma J^1$
is an isomorphism, etc.
To prove uniqueness, let
![]() $M\longrightarrow I^\bullet$
and
$M\longrightarrow I^\bullet$
and
![]() $M\longrightarrow J^\bullet$
be two minimal injective coresolutions of
$M\longrightarrow J^\bullet$
be two minimal injective coresolutions of
![]() $M$
. Then there exists a morphism of complexes of
$M$
. Then there exists a morphism of complexes of
![]() $C$
-comodules
$C$
-comodules
![]() $f:\ I^\bullet \longrightarrow J^\bullet$
making the triangular diagram
$f:\ I^\bullet \longrightarrow J^\bullet$
making the triangular diagram
![]() $M\longrightarrow I^\bullet \longrightarrow J^\bullet$
commutative. Now we have
$M\longrightarrow I^\bullet \longrightarrow J^\bullet$
commutative. Now we have
![]() ${}_\gamma I^\bullet =\textrm {Hom}_C(k,I^\bullet )$
and
${}_\gamma I^\bullet =\textrm {Hom}_C(k,I^\bullet )$
and
![]() ${}_\gamma J^\bullet =\textrm {Hom}_C(k,I^\bullet )$
. The map of complexes
${}_\gamma J^\bullet =\textrm {Hom}_C(k,I^\bullet )$
. The map of complexes
![]() $\textrm {Hom}_C(k,f):\ \textrm {Hom}_C(k,I^\bullet )\longrightarrow \textrm {Hom}_C(k,J^\bullet )$
induces an isomorphism of the cohomology spaces, as both the complexes compute
$\textrm {Hom}_C(k,f):\ \textrm {Hom}_C(k,I^\bullet )\longrightarrow \textrm {Hom}_C(k,J^\bullet )$
induces an isomorphism of the cohomology spaces, as both the complexes compute
![]() $\textrm {Ext}_C^*(k,M)$
. Since both the complexes
$\textrm {Ext}_C^*(k,M)$
. Since both the complexes
![]() ${}_\gamma I^\bullet$
and
${}_\gamma I^\bullet$
and
![]() ${}_\gamma J^\bullet$
have vanishing differentials by assumption, it follows that
${}_\gamma J^\bullet$
have vanishing differentials by assumption, it follows that
![]() $\textrm {Hom}_C(k,f)= {}_\gamma f$
is a termwise isomorphism of complexes of vector spaces. Applying Lemma 3.4(a), we conclude that
$\textrm {Hom}_C(k,f)= {}_\gamma f$
is a termwise isomorphism of complexes of vector spaces. Applying Lemma 3.4(a), we conclude that
![]() $f$
is a termwise isomorphism of complexes of
$f$
is a termwise isomorphism of complexes of
![]() $C$
-comodules.
$C$
-comodules.
The proof of part (b) is dual-analogous.
4. The left and right comodule and contramodule Ext comparison
Let
![]() $(C,\gamma )$
be a coaugmented coalgebra over a field
$(C,\gamma )$
be a coaugmented coalgebra over a field
![]() $k$
(as defined in Section 3). Then the one-dimensional
$k$
(as defined in Section 3). Then the one-dimensional
![]() $k$
-vector space
$k$
-vector space
![]() $k$
can be endowed with left and right
$k$
can be endowed with left and right
![]() $C$
-comodule and
$C$
-comodule and
![]() $C$
-contramodule structures defined in terms of
$C$
-contramodule structures defined in terms of
![]() $\gamma$
. We recall the notation
$\gamma$
. We recall the notation
![]() $\textrm {Ext}_C^*({-},{-})$
for the Ext spaces in the category of left
$\textrm {Ext}_C^*({-},{-})$
for the Ext spaces in the category of left
![]() $C$
-comodules
$C$
-comodules
![]() $C{{-\mathsf{Comod}}}$
and
$C{{-\mathsf{Comod}}}$
and
![]() $\textrm {Ext}_{C^{\mathrm{op}}}^*({-},{-})$
for the Ext spaces in the category of right
$\textrm {Ext}_{C^{\mathrm{op}}}^*({-},{-})$
for the Ext spaces in the category of right
![]() $C$
-comodules
$C$
-comodules
![]() ${{\mathsf{Comod}-}} C$
, as well as the notation
${{\mathsf{Comod}-}} C$
, as well as the notation
![]() $\textrm {Ext}^{C,*}({-},{-})$
for the Ext spaces in the category of left
$\textrm {Ext}^{C,*}({-},{-})$
for the Ext spaces in the category of left
![]() $C$
-contramodules
$C$
-contramodules
![]() $C{{-\mathsf{Contra}}}$
.
$C{{-\mathsf{Contra}}}$
.
The condition that the vector spaces
![]() $\textrm {Ext}_C^n(k,k)$
be finite-dimensional plays a key role in this paper. In this section, we explain that this condition is left-right symmetric: it holds for a coalgebra
$\textrm {Ext}_C^n(k,k)$
be finite-dimensional plays a key role in this paper. In this section, we explain that this condition is left-right symmetric: it holds for a coalgebra
![]() $C$
if and only if it holds for
$C$
if and only if it holds for
![]() $C^{\mathrm{op}}$
. Furthermore, the vector space
$C^{\mathrm{op}}$
. Furthermore, the vector space
![]() $\textrm {Ext}_C^n(k,k)$
is finite-dimensional if and only if the vector space
$\textrm {Ext}_C^n(k,k)$
is finite-dimensional if and only if the vector space
![]() $\textrm {Ext}^{C,n}(k,k)$
is. The following proposition is certainly essentially well known; we spell out the details here for the sake of completeness of the exposition.
$\textrm {Ext}^{C,n}(k,k)$
is. The following proposition is certainly essentially well known; we spell out the details here for the sake of completeness of the exposition.
Proposition 4.1.
Let
![]() $(C,\gamma )$
be a coaugmented coalgebra over
$(C,\gamma )$
be a coaugmented coalgebra over
![]() $k$
. Then there are natural isomorphisms of Ext spaces
$k$
. Then there are natural isomorphisms of Ext spaces
Moreover, in fact, the Ext-algebras
![]() $\textrm {Ext}_C^*(k,k)$
and
$\textrm {Ext}_C^*(k,k)$
and
![]() $\textrm {Ext}_{C^{\mathrm{op}}}^*(k,k)$
are naturally opposite to each other (as graded algebras),
$\textrm {Ext}_{C^{\mathrm{op}}}^*(k,k)$
are naturally opposite to each other (as graded algebras),
The module analogue of Proposition 4.1 is well known: for any augmented associative algebra
![]() $A$
over a field
$A$
over a field
![]() $k$
, there are natural isomorphisms of
$k$
, there are natural isomorphisms of
![]() $k$
-vector spaces
$k$
-vector spaces
![]() $\textrm {Ext}^n_A(k,k)\simeq \textrm {Tor}^A_n(k,k)^*\simeq \textrm {Ext}^n_{A^{\mathrm{op}}}(k,k)$
, making
$\textrm {Ext}^n_A(k,k)\simeq \textrm {Tor}^A_n(k,k)^*\simeq \textrm {Ext}^n_{A^{\mathrm{op}}}(k,k)$
, making
![]() $\textrm {Ext}_{A^{\mathrm{op}}}^*(k,k)$
the graded algebra with the opposite multiplication to
$\textrm {Ext}_{A^{\mathrm{op}}}^*(k,k)$
the graded algebra with the opposite multiplication to
![]() $\textrm {Ext}_A^*(k,k)$
.
$\textrm {Ext}_A^*(k,k)$
.
First proof.
Put
![]() $C_+=C/\gamma (k)$
. For any left
$C_+=C/\gamma (k)$
. For any left
![]() $C$
-comodule
$C$
-comodule
![]() $M$
, the reduced cobar coresolution
$M$
, the reduced cobar coresolution
is an injective coresolution of
![]() $M$
in the abelian category
$M$
in the abelian category
![]() $C{{-\mathsf{Comod}}}$
. Applying the functor
$C{{-\mathsf{Comod}}}$
. Applying the functor
![]() $\textrm {Hom}_C(k,{-})$
, we obtain a cobar complex
$\textrm {Hom}_C(k,{-})$
, we obtain a cobar complex
computing the vector spaces
![]() $\textrm {Ext}_C^*(k,M)$
. In particular, the vector spaces
$\textrm {Ext}_C^*(k,M)$
. In particular, the vector spaces
![]() $\textrm {Ext}_C^*(k,k)$
are computed by the cobar complex
$\textrm {Ext}_C^*(k,k)$
are computed by the cobar complex
[Reference Positselski and Vishik39, Section 1.1], [Reference Positselski19, Section 2.1].
Reordering the tensor factors inside every term of the complex in the opposite way identifies the complex (6) for a coalgebra
![]() $C$
with the similar complex for the opposite coalgebra
$C$
with the similar complex for the opposite coalgebra
![]() $C^{\mathrm{op}}$
. This suffices to prove the first assertion of the proposition.
$C^{\mathrm{op}}$
. This suffices to prove the first assertion of the proposition.
To prove the second assertion, one needs to observe that the obvious (free associative) multiplication on the cobar complex (6) induces a multiplication on its cohomology spaces that is precisely opposite to the composition multiplication on
![]() $\textrm {Ext}_C^*(k,k)$
. Moreover, the obvious left action of the DG-algebra (6) on the complex (5) induces a left action of the cohomology algebra of (6) on the cohomology of (5) corresponding to the natural graded right module structure over
$\textrm {Ext}_C^*(k,k)$
. Moreover, the obvious left action of the DG-algebra (6) on the complex (5) induces a left action of the cohomology algebra of (6) on the cohomology of (5) corresponding to the natural graded right module structure over
![]() $\textrm {Ext}_C^*(k,k)$
on
$\textrm {Ext}_C^*(k,k)$
on
![]() $\textrm {Ext}^*_C(k,M)$
. Thus, the isomorphism
$\textrm {Ext}^*_C(k,M)$
. Thus, the isomorphism
![]() $\textrm {Ext}_C^*(k,k)\simeq \textrm {Ext}_{C^{\mathrm{op}}}^*(k,k)$
obtained by comparing the cobar complexes (6) for
$\textrm {Ext}_C^*(k,k)\simeq \textrm {Ext}_{C^{\mathrm{op}}}^*(k,k)$
obtained by comparing the cobar complexes (6) for
![]() $C$
and
$C$
and
![]() $C^{\mathrm{op}}$
makes the multiplication on the latter Ext-algebra opposite to the one on the former one.
$C^{\mathrm{op}}$
makes the multiplication on the latter Ext-algebra opposite to the one on the former one.
This argument was sketched in [Reference Positselski19, Section 2.4]. An alternative proof of the first assertion of the proposition was suggested in [Reference Positselski19, Section 2.5].
Second proof.
Let
![]() $C{{-\mathsf{comod}}}$
and
$C{{-\mathsf{comod}}}$
and
![]() ${{\mathsf{comod}-}} C$
denote the abelian categories of finite-dimensional left and right
${{\mathsf{comod}-}} C$
denote the abelian categories of finite-dimensional left and right
![]() $C$
-comodules, respectively. One makes two observations, which, taken together, imply both the assertions of the proposition.
$C$
-comodules, respectively. One makes two observations, which, taken together, imply both the assertions of the proposition.
First, the fully faithful, exact inclusions of abelian categories
![]() $C{{-\mathsf{comod}}}\longrightarrow C{{-\mathsf{Comod}}}$
and
$C{{-\mathsf{comod}}}\longrightarrow C{{-\mathsf{Comod}}}$
and
![]() ${{\mathsf{comod}-}} C\longrightarrow {{\mathsf{Comod}-}} C$
induce isomorphisms on the Ext spaces. Moreover, the triangulated functors between bounded above derived categories
${{\mathsf{comod}-}} C\longrightarrow {{\mathsf{Comod}-}} C$
induce isomorphisms on the Ext spaces. Moreover, the triangulated functors between bounded above derived categories
![]() $\mathsf{D}^-(C{{-\mathsf{comod}}})\longrightarrow \mathsf{D}^-(C{{-\mathsf{Comod}}})$
and
$\mathsf{D}^-(C{{-\mathsf{comod}}})\longrightarrow \mathsf{D}^-(C{{-\mathsf{Comod}}})$
and
![]() $\mathsf{D}^-({{\mathsf{comod}-}} C)\longrightarrow \mathsf{D}^-({{\mathsf{Comod}-}} C)$
induced by these inclusions of abelian categories are fully faithful. This is a particular case of a well-known general result for abelian or even exact categories (see [Reference Kashiwara and Schapira12, opposite version of Proposition 1.7.11], [Reference Kashiwara and Schapira13, opposite version of Theorem 13.2.8], [Reference Keller and Hazewinkel14, opposite version of Theorem 12.1(b)], or [Reference Positselski and Schnürer37, Proposition 2.1]). The point is that for any finite-dimensional
$\mathsf{D}^-({{\mathsf{comod}-}} C)\longrightarrow \mathsf{D}^-({{\mathsf{Comod}-}} C)$
induced by these inclusions of abelian categories are fully faithful. This is a particular case of a well-known general result for abelian or even exact categories (see [Reference Kashiwara and Schapira12, opposite version of Proposition 1.7.11], [Reference Kashiwara and Schapira13, opposite version of Theorem 13.2.8], [Reference Keller and Hazewinkel14, opposite version of Theorem 12.1(b)], or [Reference Positselski and Schnürer37, Proposition 2.1]). The point is that for any finite-dimensional
![]() $C$
-comodule
$C$
-comodule
![]() $L$
, any
$L$
, any
![]() $C$
-comodule
$C$
-comodule
![]() $M$
, and any surjective
$M$
, and any surjective
![]() $C$
-comodule morphism
$C$
-comodule morphism
![]() $M\longrightarrow L$
, there exists a finite-dimensional
$M\longrightarrow L$
, there exists a finite-dimensional
![]() $C$
-subcomodule
$C$
-subcomodule
![]() $M'\subset M$
such that the composition
$M'\subset M$
such that the composition
![]() $M'\longrightarrow M\longrightarrow L$
is surjective.
$M'\longrightarrow M\longrightarrow L$
is surjective.
Second, for any finite-dimensional right
![]() $C$
-comodule
$C$
-comodule
![]() $N$
, the dual vector space
$N$
, the dual vector space
![]() $N^*$
is naturally a finite-dimensional left
$N^*$
is naturally a finite-dimensional left
![]() $C$
-comodule. Here, it helps to notice that for any such
$C$
-comodule. Here, it helps to notice that for any such
![]() $N$
there exists a finite-dimensional subcoalgebra
$N$
there exists a finite-dimensional subcoalgebra
![]() $E\subset C$
such that the
$E\subset C$
such that the
![]() $C$
-comodule structure on
$C$
-comodule structure on
![]() $N$
arises from an
$N$
arises from an
![]() $E$
-comodule structure [Reference Positselski36, Lemma 3.1(c)]. Consequently, there is a natural anti-equivalence of abelian categories
$E$
-comodule structure [Reference Positselski36, Lemma 3.1(c)]. Consequently, there is a natural anti-equivalence of abelian categories
taking the right
![]() $C$
-comodule
$C$
-comodule
![]() $k$
to the left
$k$
to the left
![]() $C$
-comodule
$C$
-comodule
![]() $k$
. This anti-equivalence induces the desired anti-isomorphism of the Ext algebras.
$k$
. This anti-equivalence induces the desired anti-isomorphism of the Ext algebras.
Lemma 4.2.
Let
![]() $C$
be a coalgebra over a field
$C$
be a coalgebra over a field
![]() $k$
. Let
$k$
. Let
![]() $M\in {{\mathsf{Comod}-}} C$
be a right
$M\in {{\mathsf{Comod}-}} C$
be a right
![]() $C$
-comodule and
$C$
-comodule and
![]() $L\in {{\mathsf{comod}-}} C$
be a finite-dimensional right
$L\in {{\mathsf{comod}-}} C$
be a finite-dimensional right
![]() $C$
-comodule. Then the vector space of left
$C$
-comodule. Then the vector space of left
![]() $C$
-contramodule homomorpisms
$C$
-contramodule homomorpisms
![]() $M^*\longrightarrow L^*$
is naturally isomorphic to the double dual vector space to the vector space of right
$M^*\longrightarrow L^*$
is naturally isomorphic to the double dual vector space to the vector space of right
![]() $C$
-comodule homomorphisms
$C$
-comodule homomorphisms
![]() $L\longrightarrow M$
,
$L\longrightarrow M$
,
This isomorphism identifies the map
![]() $\textrm {Hom}_{C^{\mathrm{op}}}(L,M)\longrightarrow \textrm {Hom}^C(M^*,L^*)$
induced by the contravariant functor of vector space dualization
$\textrm {Hom}_{C^{\mathrm{op}}}(L,M)\longrightarrow \textrm {Hom}^C(M^*,L^*)$
induced by the contravariant functor of vector space dualization
![]() $N\longmapsto N^*:\ {{\mathsf{Comod}-}} C\longrightarrow C{{-\mathsf{Contra}}}$
with the natural inclusion
$N\longmapsto N^*:\ {{\mathsf{Comod}-}} C\longrightarrow C{{-\mathsf{Contra}}}$
with the natural inclusion
![]() $\textrm {Hom}_{C^{\mathrm{op}}}(L,M)\longrightarrow \textrm {Hom}_{C^{\mathrm{op}}}(L,M)^{**}$
of a vector space
$\textrm {Hom}_{C^{\mathrm{op}}}(L,M)\longrightarrow \textrm {Hom}_{C^{\mathrm{op}}}(L,M)^{**}$
of a vector space
![]() $\textrm {Hom}_{C^{\mathrm{op}}}(L,M)$
into its double dual vector space.
$\textrm {Hom}_{C^{\mathrm{op}}}(L,M)$
into its double dual vector space.
Proof.
Notice that for any
![]() $k$
-vector space
$k$
-vector space
![]() $V$
and any finite-dimensional
$V$
and any finite-dimensional
![]() $k$
-vector space
$k$
-vector space
![]() $W$
there is a natural isomorphism of
$W$
there is a natural isomorphism of
![]() $k$
-vector spaces
$k$
-vector spaces
where
![]() $V^*=\textrm {Hom}_k(V,k)$
and
$V^*=\textrm {Hom}_k(V,k)$
and
![]() $W^*=\textrm {Hom}_k(W,k)$
. The isomorphism (8) identifies the map
$W^*=\textrm {Hom}_k(W,k)$
. The isomorphism (8) identifies the map
![]() $\textrm {Hom}_k(W,V)\longrightarrow \textrm {Hom}_k(V^*,W^*)$
induced by the contravariant functor
$\textrm {Hom}_k(W,V)\longrightarrow \textrm {Hom}_k(V^*,W^*)$
induced by the contravariant functor
![]() $U\longmapsto U^*:\ k{{-\mathsf{Vect}}}\longrightarrow k{{-\mathsf{Vect}}}$
with the natural inclusion
$U\longmapsto U^*:\ k{{-\mathsf{Vect}}}\longrightarrow k{{-\mathsf{Vect}}}$
with the natural inclusion
![]() $\textrm {Hom}_k(W,V)\longrightarrow \textrm {Hom}_k(W,V)^{**}$
of a vector space
$\textrm {Hom}_k(W,V)\longrightarrow \textrm {Hom}_k(W,V)^{**}$
of a vector space
![]() $\textrm {Hom}_k(W,V)$
into its double dual vector space.
$\textrm {Hom}_k(W,V)$
into its double dual vector space.
Now, for any two right
![]() $C$
-comodules
$C$
-comodules
![]() $L$
and
$L$
and
![]() $M$
, the vector space
$M$
, the vector space
![]() $\textrm {Hom}_{C^{\mathrm{op}}}(L,M)$
is the kernel of (the difference of) a natural pair of maps
$\textrm {Hom}_{C^{\mathrm{op}}}(L,M)$
is the kernel of (the difference of) a natural pair of maps
![]() $\textrm {Hom}_k(L,M)\rightrightarrows \textrm {Hom}_k(L,\ M\otimes _k C)$
,
$\textrm {Hom}_k(L,M)\rightrightarrows \textrm {Hom}_k(L,\ M\otimes _k C)$
,
For any two left
![]() $C$
-contramodules
$C$
-contramodules
![]() $P$
and
$P$
and
![]() $Q$
, the vector space
$Q$
, the vector space
![]() $\textrm {Hom}^C(P,Q)$
is the kernel of (the difference of) a natural pair of maps
$\textrm {Hom}^C(P,Q)$
is the kernel of (the difference of) a natural pair of maps
![]() $\textrm {Hom}_k(P,Q)\rightrightarrows \textrm {Hom}_k(\textrm {Hom}_k(C,P),Q)$
,
$\textrm {Hom}_k(P,Q)\rightrightarrows \textrm {Hom}_k(\textrm {Hom}_k(C,P),Q)$
,
In particular, for
![]() $P=M^*$
and
$P=M^*$
and
![]() $Q=L^*$
, we have
$Q=L^*$
, we have
It remains to use the natural isomorphism (8) in order to show that the double dual vector space functor
![]() $U\longmapsto U^{**}$
takes the rightmost pair of parallel morphisms in the sequence (9) to the rightmost pair of parallel morphisms in the sequence (11) for a finite-dimensional
$U\longmapsto U^{**}$
takes the rightmost pair of parallel morphisms in the sequence (9) to the rightmost pair of parallel morphisms in the sequence (11) for a finite-dimensional
![]() $C$
-comodule
$C$
-comodule
![]() $L$
.
$L$
.
Proposition 4.3.
Let
![]() $(C,\gamma )$
be a coaugmented coalgebra over
$(C,\gamma )$
be a coaugmented coalgebra over
![]() $k$
. Then the vector space
$k$
. Then the vector space
![]() $\textrm {Ext}^{C,n}(k,k)$
is naturally isomorphic to the double dual vector space to the vector space
$\textrm {Ext}^{C,n}(k,k)$
is naturally isomorphic to the double dual vector space to the vector space
![]() $\textrm {Ext}_{C^{\mathrm{op}}}^n(k,k)$
,
$\textrm {Ext}_{C^{\mathrm{op}}}^n(k,k)$
,
This isomorphism identifies the map
![]() $\textrm {Ext}_{C^{\mathrm{op}}}^n(k,k)\longrightarrow \textrm {Ext}^{C,n}(k,k)$
induced by the exact contravariant functor of vector space dualization
$\textrm {Ext}_{C^{\mathrm{op}}}^n(k,k)\longrightarrow \textrm {Ext}^{C,n}(k,k)$
induced by the exact contravariant functor of vector space dualization
![]() $N\longmapsto N^*:\ {{\mathsf{Comod}-}} C\longrightarrow C{{-\mathsf{Contra}}}$
with the natural inclusion
$N\longmapsto N^*:\ {{\mathsf{Comod}-}} C\longrightarrow C{{-\mathsf{Contra}}}$
with the natural inclusion
![]() $\textrm {Ext}^n_{C^{\mathrm{op}}}(k,k)\longrightarrow \textrm {Ext}^n_{C^{\mathrm{op}}}(k,k)^{**}$
of a vector space
$\textrm {Ext}^n_{C^{\mathrm{op}}}(k,k)\longrightarrow \textrm {Ext}^n_{C^{\mathrm{op}}}(k,k)^{**}$
of a vector space
![]() $\textrm {Ext}^n_{C^{\mathrm{op}}}(k,k)$
into its double dual vector space.
$\textrm {Ext}^n_{C^{\mathrm{op}}}(k,k)$
into its double dual vector space.
Proof.
This observation goes back to the discussion in [Reference Positselski20, Section A.1.2]. The point is that the functor
![]() $N\longmapsto N^*:\ {{\mathsf{Comod}-}} C \longrightarrow C{{-\mathsf{Contra}}}$
takes injective right
$N\longmapsto N^*:\ {{\mathsf{Comod}-}} C \longrightarrow C{{-\mathsf{Contra}}}$
takes injective right
![]() $C$
-comodules to projective left
$C$
-comodules to projective left
![]() $C$
-contramodules, which makes it easy to compute the induced map of the Ext spaces.
$C$
-contramodules, which makes it easy to compute the induced map of the Ext spaces.
For any coalgebra
![]() $C$
and any right
$C$
and any right
![]() $C$
-comodule
$C$
-comodule
![]() $M$
, pick an injective coresolution
$M$
, pick an injective coresolution
of
![]() $M$
in the abelian category
$M$
in the abelian category
![]() ${{\mathsf{Comod}-}} C$
. Applying the dual vector space functor
${{\mathsf{Comod}-}} C$
. Applying the dual vector space functor
![]() $\textrm {Hom}_k({-},k)$
to the complex (12), we obtain the complex
$\textrm {Hom}_k({-},k)$
to the complex (12), we obtain the complex
which is a projective resolution of the left
![]() $C$
-contramodule
$C$
-contramodule
![]() $M^*=\textrm {Hom}_k(M,k)$
.
$M^*=\textrm {Hom}_k(M,k)$
.
Now let
![]() $L$
be a another right
$L$
be a another right
![]() $C$
-comodule. Then one can compute the vector spaces
$C$
-comodule. Then one can compute the vector spaces
![]() $\textrm {Ext}^n_{C^{\mathrm{op}}}(L,M)$
as the cohomology spaces of the complex obtained by applying the functor
$\textrm {Ext}^n_{C^{\mathrm{op}}}(L,M)$
as the cohomology spaces of the complex obtained by applying the functor
![]() $\textrm {Hom}_{C^{\mathrm{op}}}(L,{-})$
to the coresolution (12). Similarly, one can compute the vector spaces
$\textrm {Hom}_{C^{\mathrm{op}}}(L,{-})$
to the coresolution (12). Similarly, one can compute the vector spaces
![]() $\textrm {Ext}^{C,n}(M^*,L^*)$
as the cohomology spaces of the complex obtained by applying the functor
$\textrm {Ext}^{C,n}(M^*,L^*)$
as the cohomology spaces of the complex obtained by applying the functor
![]() $\textrm {Hom}^C({-},L^*)$
to the resolution (13). Taking into account Lemma 4.2, we obtain a natural isomorphism of complexes
$\textrm {Hom}^C({-},L^*)$
to the resolution (13). Taking into account Lemma 4.2, we obtain a natural isomorphism of complexes
inducing a natural isomorphism of the cohomology spaces
for all right
![]() $C$
-comodules
$C$
-comodules
![]() $M$
, all finite-dimensional right
$M$
, all finite-dimensional right
![]() $C$
-comodules
$C$
-comodules
![]() $L$
, and all integers
$L$
, and all integers
![]() $n\ge 0$
. Moreover, it follows from the second assertion of the lemma that the map
$n\ge 0$
. Moreover, it follows from the second assertion of the lemma that the map
![]() $\textrm {Ext}^n_{C^{\mathrm{op}}}(L,M)\longrightarrow \textrm {Ext}^{C,n}(M^*,L^*)$
induced by the functor
$\textrm {Ext}^n_{C^{\mathrm{op}}}(L,M)\longrightarrow \textrm {Ext}^{C,n}(M^*,L^*)$
induced by the functor
![]() $N\longmapsto N^*:\ {{\mathsf{Comod}-}} C\longrightarrow C{{-\mathsf{Contra}}}$
agrees with the obvious map
$N\longmapsto N^*:\ {{\mathsf{Comod}-}} C\longrightarrow C{{-\mathsf{Contra}}}$
agrees with the obvious map
![]() $\textrm {Ext}^n_{C^{\mathrm{op}}}(L,M)\longrightarrow \textrm {Ext}^n_{C^{\mathrm{op}}}(L,M)^{**}$
.
$\textrm {Ext}^n_{C^{\mathrm{op}}}(L,M)\longrightarrow \textrm {Ext}^n_{C^{\mathrm{op}}}(L,M)^{**}$
.
5. Weakly finite Koszulity implies comodule Ext isomorphism
The aim of this section is to prove the following theorem.
Theorem 5.1.
Let
![]() $C$
be a conilpotent coalgebra over a field
$C$
be a conilpotent coalgebra over a field
![]() $k$
and
$k$
and
![]() $n\ge 0$
be an integer such that the vector space
$n\ge 0$
be an integer such that the vector space
![]() $\textrm {Ext}^i_C(k,k)$
is finite-dimensional for all
$\textrm {Ext}^i_C(k,k)$
is finite-dimensional for all
![]() $1\le i\le n$
. Then the map of Ext spaces
$1\le i\le n$
. Then the map of Ext spaces
induced by the inclusion functor
![]() $\Upsilon :\ C{{-\mathsf{Comod}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
is an isomorphism for all left
$\Upsilon :\ C{{-\mathsf{Comod}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
is an isomorphism for all left
![]() $C$
-comodules
$C$
-comodules
![]() $L$
and
$L$
and
![]() $M$
and all
$M$
and all
![]() $0\le i\le n$
.
$0\le i\le n$
.
We start with a lemma describing some vector spaces of morphisms in the category of left
![]() $C^*$
-modules for a coalgebra
$C^*$
-modules for a coalgebra
![]() $C$
. A right
$C$
. A right
![]() $C$
-comodule
$C$
-comodule
![]() $N$
is said to be finitely cogenerated if it is a subcomodule of a cofree
$N$
is said to be finitely cogenerated if it is a subcomodule of a cofree
![]() $C$
-comodule
$C$
-comodule
![]() $V\otimes _k C$
with a finite-dimensional vector space of cogenerators
$V\otimes _k C$
with a finite-dimensional vector space of cogenerators
![]() $V$
.
$V$
.
Lemma 5.2.
Let
![]() $C$
be a coalgebra over
$C$
be a coalgebra over
![]() $k$
, let
$k$
, let
![]() $N$
be a right
$N$
be a right
![]() $C$
-comodule, and let
$C$
-comodule, and let
![]() $U$
be a
$U$
be a
![]() $k$
-vector space. Then there is a natural monomorphism of
$k$
-vector space. Then there is a natural monomorphism of
![]() $k$
-vector spaces
$k$
-vector spaces
which is an isomorphism whenever
![]() $N$
is a finitely cogenerated injective
$N$
is a finitely cogenerated injective
![]() $C$
-comodule. Here the left
$C$
-comodule. Here the left
![]() $C^*$
-module structure on
$C^*$
-module structure on
![]() $N^*=\textrm {Hom}_k(N,k)$
is obtained by dualizing the right
$N^*=\textrm {Hom}_k(N,k)$
is obtained by dualizing the right
![]() $C^*$
-module structure on
$C^*$
-module structure on
![]() $N$
(or equivalently, by applying the forgetful functor to the natural left
$N$
(or equivalently, by applying the forgetful functor to the natural left
![]() $C$
-contramodule structure on
$C$
-contramodule structure on
![]() $N^*$
), while the left
$N^*$
), while the left
![]() $C^*$
-module structure on
$C^*$
-module structure on
![]() $C\otimes _kU$
comes from the cofree left
$C\otimes _kU$
comes from the cofree left
![]() $C$
-comodule structure.
$C$
-comodule structure.
Proof.
The map
![]() $\eta _{N,U}$
is defined by the formula
$\eta _{N,U}$
is defined by the formula
for all
![]() $x\in N$
,
$x\in N$
,
![]() $u\in U$
, and
$u\in U$
, and
![]() $f\in N^*$
. Here,
$f\in N^*$
. Here,
![]() $\nu (x)=x_{(0)}\otimes x_{(1)}\in N\otimes _k C$
is a notation for the right
$\nu (x)=x_{(0)}\otimes x_{(1)}\in N\otimes _k C$
is a notation for the right
![]() $C$
-coaction map
$C$
-coaction map
![]() $\nu :\ N\longrightarrow N\otimes _kC$
.
$\nu :\ N\longrightarrow N\otimes _kC$
.
To prove the isomorphism assertion for a finitely cogenerated injective
![]() $C$
-comodule
$C$
-comodule
![]() $N$
, it suffices to consider the case
$N$
, it suffices to consider the case
![]() $N=V\otimes _kC$
, where
$N=V\otimes _kC$
, where
![]() $\dim _kV\lt \infty$
. In this case,
$\dim _kV\lt \infty$
. In this case,
![]() $N^*=C^*\otimes _k V^*$
is a free left
$N^*=C^*\otimes _k V^*$
is a free left
![]() $C^*$
-module, so
$C^*$
-module, so
![]() $\textrm {Hom}_{C^*}(N^*,\ C\otimes _kU)=\textrm {Hom}_k(V^*,\ C\otimes _kU)= V\otimes _kC\otimes _kU=N\otimes _kU$
.
$\textrm {Hom}_{C^*}(N^*,\ C\otimes _kU)=\textrm {Hom}_k(V^*,\ C\otimes _kU)= V\otimes _kC\otimes _kU=N\otimes _kU$
.
To prove that
![]() $\eta _{N,U}$
is an injective map for any
$\eta _{N,U}$
is an injective map for any
![]() $C$
-comodule
$C$
-comodule
![]() $N$
, consider the
$N$
, consider the
![]() $k$
-linear map
$k$
-linear map
induced by the counit map
![]() $\epsilon :\ C\longrightarrow k$
. Notice that the counit is not a
$\epsilon :\ C\longrightarrow k$
. Notice that the counit is not a
![]() $C$
-comodule morphism, and consequently not a
$C$
-comodule morphism, and consequently not a
![]() $C^*$
-module morphism, but only a linear map of
$C^*$
-module morphism, but only a linear map of
![]() $k$
-vector spaces. The composition
$k$
-vector spaces. The composition
is the natural injective map of
![]() $k$
-vector spaces
$k$
-vector spaces
![]() $N\otimes _kU\longrightarrow \textrm {Hom}_k(N^*,U)$
(defined for any two vector spaces
$N\otimes _kU\longrightarrow \textrm {Hom}_k(N^*,U)$
(defined for any two vector spaces
![]() $U$
and
$U$
and
![]() $W=N$
). Since the composition is a monomorphism, so is the map
$W=N$
). Since the composition is a monomorphism, so is the map
![]() $\eta =\eta _{N,U}$
.
$\eta =\eta _{N,U}$
.
Let
![]() $C=(C,\gamma )$
be a coaugmented coalgebra. For every
$C=(C,\gamma )$
be a coaugmented coalgebra. For every
![]() $m\ge 0$
, denote by
$m\ge 0$
, denote by
![]() $F_mC\subset C$
the kernel of the composition
$F_mC\subset C$
the kernel of the composition
![]() $C\longrightarrow C^{\otimes m+1}\longrightarrow (C/\gamma (k))^{\otimes m+1}$
, where
$C\longrightarrow C^{\otimes m+1}\longrightarrow (C/\gamma (k))^{\otimes m+1}$
, where
![]() $\mu ^{(m)}:\ C\longrightarrow C^{\otimes m+1}$
is the iterated comultiplication map and
$\mu ^{(m)}:\ C\longrightarrow C^{\otimes m+1}$
is the iterated comultiplication map and
![]() $C^{\otimes m+1}\longrightarrow (C/\gamma (k))^{\otimes m+1}$
is the natural surjection. So one has
$C^{\otimes m+1}\longrightarrow (C/\gamma (k))^{\otimes m+1}$
is the natural surjection. So one has
![]() $F_{-1}C=0$
and
$F_{-1}C=0$
and
![]() $F_0C=\gamma (k)\subset C$
. One can check that
$F_0C=\gamma (k)\subset C$
. One can check that
![]() $F$
is a comultiplicative filtration on
$F$
is a comultiplicative filtration on
![]() $C$
, that is,
$C$
, that is,
for all
![]() $m\ge 0$
[Reference Positselski and Vishik39, Section 3.1].
$m\ge 0$
[Reference Positselski and Vishik39, Section 3.1].
Let
![]() $L$
be a left
$L$
be a left
![]() $C$
-comodule. Denote by
$C$
-comodule. Denote by
![]() $F_mL\subset L$
the full preimage of the subspace
$F_mL\subset L$
the full preimage of the subspace
![]() $F_mC\otimes _k L\subset C\otimes _k L$
under the coaction map
$F_mC\otimes _k L\subset C\otimes _k L$
under the coaction map
![]() $\nu :\ L\longrightarrow C\otimes _k L$
. So one has
$\nu :\ L\longrightarrow C\otimes _k L$
. So one has
![]() $F_{-1}L=0$
and
$F_{-1}L=0$
and
![]() $F_0L={}_\gamma L$
(in the notation of Section 3). One can check that
$F_0L={}_\gamma L$
(in the notation of Section 3). One can check that
![]() $F$
is a comultiplicative filtration on
$F$
is a comultiplicative filtration on
![]() $L$
compatible with the filtration
$L$
compatible with the filtration
![]() $F$
on
$F$
on
![]() $C$
, that is,
$C$
, that is,
for all
![]() $m\ge 0$
[Reference Positselski19, Section 4.1].
$m\ge 0$
[Reference Positselski19, Section 4.1].
In other words, this means that
![]() $F_mL$
is a
$F_mL$
is a
![]() $C$
-subcomodule of
$C$
-subcomodule of
![]() $L$
for every
$L$
for every
![]() $m\ge 0$
and the successive quotient
$m\ge 0$
and the successive quotient
![]() $C$
-comodules
$C$
-comodules
![]() $F_mL/F_{m-1}L$
are trivial (i.e., the coaction of
$F_mL/F_{m-1}L$
are trivial (i.e., the coaction of
![]() $C$
in them is induced by the coaugmentation
$C$
in them is induced by the coaugmentation
![]() $\gamma$
). In fact, one has
$\gamma$
). In fact, one has
![]() $F_mL/F_{m-1}L={}_\gamma (L/F_{m-1}L)\subset L/F_{m-1}L$
for every
$F_mL/F_{m-1}L={}_\gamma (L/F_{m-1}L)\subset L/F_{m-1}L$
for every
![]() $m\ge 1$
.
$m\ge 1$
.
By the definition, a coaugmented coalgebra
![]() $C$
is conilpotent if and only if
$C$
is conilpotent if and only if
![]() $C=\bigcup _{m=0}^\infty F_mC$
(i.e., the increasing filtration
$C=\bigcup _{m=0}^\infty F_mC$
(i.e., the increasing filtration
![]() $F$
on
$F$
on
![]() $C$
is exhaustive). In this case, it follows that
$C$
is exhaustive). In this case, it follows that
![]() $L=\bigcup _{m=0}^\infty F_mL$
, that is the increasing filtration
$L=\bigcup _{m=0}^\infty F_mL$
, that is the increasing filtration
![]() $F$
on any
$F$
on any
![]() $C$
-comodule is exhaustive as well.
$C$
-comodule is exhaustive as well.
Proof of Theorem
5.1. The argument resembles the proofs of the comodule Ext comparison theorems in [Reference Positselski35, Sections 5.4 and 5.7] (see specifically [Reference Positselski35, Theorem 5.21]). Notice first of all that the functor
![]() $\Upsilon$
is always fully faithful by [Reference Sweedler44, Propositions 2.1.1–2.1.2 and Theorem 2.1.3(e)].
$\Upsilon$
is always fully faithful by [Reference Sweedler44, Propositions 2.1.1–2.1.2 and Theorem 2.1.3(e)].
According to Lemma A.5 from the appendix, in order to prove the theorem it suffices to show that
![]() $\textrm {Ext}^i_{C^*}(L,J)=0$
for all left
$\textrm {Ext}^i_{C^*}(L,J)=0$
for all left
![]() $C$
-comodules
$C$
-comodules
![]() $L$
, all injective left
$L$
, all injective left
![]() $C$
-comodules
$C$
-comodules
![]() $J$
, and all integers
$J$
, and all integers
![]() $1\le i\le n$
. Equivalently, this means that the space
$1\le i\le n$
. Equivalently, this means that the space
![]() $\textrm {Ext}^i_{C^*}(L,\ C\otimes _kU)$
should vanish for all
$\textrm {Ext}^i_{C^*}(L,\ C\otimes _kU)$
should vanish for all
![]() $k$
-vector spaces
$k$
-vector spaces
![]() $U$
and
$U$
and
![]() $1\le i\le n$
.
$1\le i\le n$
.
According to the discussion preceding this proof, the
![]() $C$
-comodule
$C$
-comodule
![]() $L$
has a natural increasing filtration with (direct sums of) the trivial
$L$
has a natural increasing filtration with (direct sums of) the trivial
![]() $C$
-comodule
$C$
-comodule
![]() $k$
as the successive quotients. Using the Eklof lemma [Reference Eklof and Trlifaj6, Lemma 1], the problem reduces to showing that
$k$
as the successive quotients. Using the Eklof lemma [Reference Eklof and Trlifaj6, Lemma 1], the problem reduces to showing that
![]() $\textrm {Ext}^i_{C^*}(k,\ C\otimes _kU)=0$
for all
$\textrm {Ext}^i_{C^*}(k,\ C\otimes _kU)=0$
for all
![]() $k$
-vector spaces
$k$
-vector spaces
![]() $U$
.
$U$
.
Let
be a minimal injective/cofree coresolution of the right
![]() $C$
-comodule
$C$
-comodule
![]() $k$
, as per Corollary 3.6(a) and Proposition 3.7(a). Here
$k$
, as per Corollary 3.6(a) and Proposition 3.7(a). Here
![]() $V_i$
,
$V_i$
,
![]() $i\ge 0$
, are some
$i\ge 0$
, are some
![]() $k$
-vector spaces. Computing the Ext spaces
$k$
-vector spaces. Computing the Ext spaces
![]() $\textrm {Ext}_{C^{\mathrm{op}}}^*(k,k)$
using the injective coresolution (14), we obtain isomorphisms
$\textrm {Ext}_{C^{\mathrm{op}}}^*(k,k)$
using the injective coresolution (14), we obtain isomorphisms
![]() $V_i\simeq \textrm {Ext}_{C^{\mathrm{op}}}^i(k,k)$
(in particular,
$V_i\simeq \textrm {Ext}_{C^{\mathrm{op}}}^i(k,k)$
(in particular,
![]() $V_0\simeq k$
). Furthermore, Proposition 4.1 provides isomorphisms
$V_0\simeq k$
). Furthermore, Proposition 4.1 provides isomorphisms
![]() $\textrm {Ext}_{C^{\mathrm{op}}}^i(k,k)\simeq \textrm {Ext}_C^i(k,k)$
. So the vector space
$\textrm {Ext}_{C^{\mathrm{op}}}^i(k,k)\simeq \textrm {Ext}_C^i(k,k)$
. So the vector space
![]() $V_i$
is finite-dimensional for
$V_i$
is finite-dimensional for
![]() $0\le i\le n$
by assumption.
$0\le i\le n$
by assumption.
Applying the dual vector space functor
![]() $\textrm {Hom}_k({-},k)$
to the complex of right
$\textrm {Hom}_k({-},k)$
to the complex of right
![]() $C$
-comodules (14), we obtain a resolution of the left
$C$
-comodules (14), we obtain a resolution of the left
![]() $C^*$
-module
$C^*$
-module
![]() $k$
,
$k$
,
The exact complex of left
![]() $C^*$
-modules (15) starts and proceeds up to the homological degree
$C^*$
-modules (15) starts and proceeds up to the homological degree
![]() $n$
as a resolution by finitely generated projective
$n$
as a resolution by finitely generated projective
![]() $C^*$
-modules before turning into a resolution by some arbitrary
$C^*$
-modules before turning into a resolution by some arbitrary
![]() $C^*$
-modules (in fact, projective left
$C^*$
-modules (in fact, projective left
![]() $C$
-contramodules) from the homological degree
$C$
-contramodules) from the homological degree
![]() $n+1$
on.
$n+1$
on.
For every
![]() $0\le i\le n+1$
and any left
$0\le i\le n+1$
and any left
![]() $C^*$
-module
$C^*$
-module
![]() $J$
, the space
$J$
, the space
![]() $\textrm {Ext}^i_{C^*}(k,J)$
can be computed as the degree
$\textrm {Ext}^i_{C^*}(k,J)$
can be computed as the degree
![]() $i$
cohomology space of the complex obtained by applying the functor
$i$
cohomology space of the complex obtained by applying the functor
![]() $\textrm {Hom}_{C^*}({-},J)$
to the resolution (15) of the left
$\textrm {Hom}_{C^*}({-},J)$
to the resolution (15) of the left
![]() $C^*$
-module
$C^*$
-module
![]() $k$
(see Lemma A.1). We are only interested in
$k$
(see Lemma A.1). We are only interested in
![]() $0\le i\le n$
now, so let us write down the resulting complex in the cohomological degrees from
$0\le i\le n$
now, so let us write down the resulting complex in the cohomological degrees from
![]() $0$
to
$0$
to
![]() $n+1$
. It has the form
$n+1$
. It has the form
which for
![]() $J=C\otimes _kU$
turns into
$J=C\otimes _kU$
turns into
In the cohomological degrees
![]() $\le n$
, the complex (16) can be simply obtained by applying the vector space tensor product functor
$\le n$
, the complex (16) can be simply obtained by applying the vector space tensor product functor
![]() ${-}\otimes _kU$
to the coresolution (14). This follows from Lemma 5.2. Consequently, the complex (16) is exact in the cohomological degrees
${-}\otimes _kU$
to the coresolution (14). This follows from Lemma 5.2. Consequently, the complex (16) is exact in the cohomological degrees
![]() $0\lt i\lt n$
. It is only the complicated rightmost term of (16) that remains to be dealt with.
$0\lt i\lt n$
. It is only the complicated rightmost term of (16) that remains to be dealt with.
Finally, the same Lemma 5.2 provides a commutative square diagram of
![]() $k$
-linear maps
$k$
-linear maps

where the leftmost vertical isomorphism is
![]() $\eta =\eta _{V_n\otimes _kC,\ U}$
, the rightmost vertical monomorphism is
$\eta =\eta _{V_n\otimes _kC,\ U}$
, the rightmost vertical monomorphism is
![]() $\eta =\eta _{V_{n+1}\otimes _kC,\ U}$
, the horizontal arrows are induced by the differential
$\eta =\eta _{V_{n+1}\otimes _kC,\ U}$
, the horizontal arrows are induced by the differential
![]() $\tau _n$
in the coresolution (14), and the diagonal composition
$\tau _n$
in the coresolution (14), and the diagonal composition
![]() $\theta$
is the rightmost differential in the complex (16). Now it is clear from the diagram (17) that the kernel of the map
$\theta$
is the rightmost differential in the complex (16). Now it is clear from the diagram (17) that the kernel of the map
![]() $\theta :\ V_n\otimes _k C\otimes _k U\longrightarrow \textrm {Hom}_{C^*}((V_{n+1}\otimes _k C)^*,\ C\otimes _kU)$
coincides with the kernel of the map
$\theta :\ V_n\otimes _k C\otimes _k U\longrightarrow \textrm {Hom}_{C^*}((V_{n+1}\otimes _k C)^*,\ C\otimes _kU)$
coincides with the kernel of the map
![]() $\tau _n\otimes _kU\;:\; V_n\otimes _k C\otimes _k U\longrightarrow V_{n+1}\otimes _k C\otimes _k U$
(because the rightmost vertical map
$\tau _n\otimes _kU\;:\; V_n\otimes _k C\otimes _k U\longrightarrow V_{n+1}\otimes _k C\otimes _k U$
(because the rightmost vertical map
![]() $\eta$
is injective). Thus, exactness of the coresolution (14) implies exactness of the complex (16) in the cohomological degree
$\eta$
is injective). Thus, exactness of the coresolution (14) implies exactness of the complex (16) in the cohomological degree
![]() $n$
as well.
$n$
as well.
Corollary 5.3.
Let
![]() $C$
be a conilpotent coalgebra over a field
$C$
be a conilpotent coalgebra over a field
![]() $k$
and
$k$
and
![]() $n\ge 0$
be an integer such that the vector space
$n\ge 0$
be an integer such that the vector space
![]() $\textrm {Ext}_C^i(k,k)$
is finite-dimensional for all
$\textrm {Ext}_C^i(k,k)$
is finite-dimensional for all
![]() $1\le i\le n$
. Then the map of Ext spaces
$1\le i\le n$
. Then the map of Ext spaces
induced by the comodule inclusion functor
![]() $\Upsilon :\ C{{-\mathsf{Comod}}} \longrightarrow C^*{{-\mathsf{Mod}}}$
is injective for all left
$\Upsilon :\ C{{-\mathsf{Comod}}} \longrightarrow C^*{{-\mathsf{Mod}}}$
is injective for all left
![]() $C$
-comodules
$C$
-comodules
![]() $L$
and
$L$
and
![]() $M$
and all
$M$
and all
![]() $0\le i\le n+1$
.
$0\le i\le n+1$
.
6. Comodule Ext isomorphism implies weakly finite Koszulity
The aim of this section is to prove the following theorem.
Theorem 6.1.
Let
![]() $C$
be a conilpotent coalgebra over a field
$C$
be a conilpotent coalgebra over a field
![]() $k$
and
$k$
and
![]() $n\ge 1$
be the minimal integer for which the vector space
$n\ge 1$
be the minimal integer for which the vector space
![]() $\textrm {Ext}_C^n(k,k)$
is infinite-dimensional. Then the map
$\textrm {Ext}_C^n(k,k)$
is infinite-dimensional. Then the map
![]() $\textrm {Ext}^n_C(k,k)\longrightarrow \textrm {Ext}^n_{C^*}(k,k)$
induced by the comodule inclusion functor
$\textrm {Ext}^n_C(k,k)\longrightarrow \textrm {Ext}^n_{C^*}(k,k)$
induced by the comodule inclusion functor
![]() $\Upsilon :\ C{{-\mathsf{Comod}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
is injective, but not surjective. In fact, if
$\Upsilon :\ C{{-\mathsf{Comod}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
is injective, but not surjective. In fact, if
![]() $\lambda$
is the dimension cardinality of the
$\lambda$
is the dimension cardinality of the
![]() $k$
-vector space
$k$
-vector space
![]() $\textrm {Ext}^n_C(k,k)$
and
$\textrm {Ext}^n_C(k,k)$
and
![]() $\kappa$
is the cardinality of the field
$\kappa$
is the cardinality of the field
![]() $k$
, then the dimension cardinality of
$k$
, then the dimension cardinality of
![]() $\textrm {Ext}^n_{C^*}(k,k)$
is equal to
$\textrm {Ext}^n_{C^*}(k,k)$
is equal to
![]() $\kappa ^{\kappa ^\lambda }$
.
$\kappa ^{\kappa ^\lambda }$
.
The following lemma computing the dimension cardinality of the dual vector space is a classical result.
Lemma 6.2.
Let
![]() $V$
be an infinite-dimensional vector space of dimension cardinality
$V$
be an infinite-dimensional vector space of dimension cardinality
![]() $\lambda$
over a field
$\lambda$
over a field
![]() $k$
of cardinality
$k$
of cardinality
![]() $\kappa$
. Then the dimension cardinality of the dual
$\kappa$
. Then the dimension cardinality of the dual
![]() $k$
-vector space
$k$
-vector space
![]() $V^*=\textrm {Hom}_k(V,k)$
is equal to
$V^*=\textrm {Hom}_k(V,k)$
is equal to
![]() $\kappa ^\lambda$
.
$\kappa ^\lambda$
.
Proof. This is [Reference Jacobson11, Section IX.5].
Let
![]() $C$
be a conilpotent coalgebra. Then the vector space
$C$
be a conilpotent coalgebra. Then the vector space
![]() $\textrm {Ext}^1_C(k,k)$
can be interpreted as the space of cogenerators of the coalgebra
$\textrm {Ext}^1_C(k,k)$
can be interpreted as the space of cogenerators of the coalgebra
![]() $C$
(we refer to [Reference Positselski26, Lemma 5.2] for a discussion). So we will say that a conilpotent coalgebra
$C$
(we refer to [Reference Positselski26, Lemma 5.2] for a discussion). So we will say that a conilpotent coalgebra
![]() $C$
is finitely cogenerated if the vector space
$C$
is finitely cogenerated if the vector space
![]() $\textrm {Ext}^1_C(k,k)$
is finite-dimensional.
$\textrm {Ext}^1_C(k,k)$
is finite-dimensional.
For any coaugmented coalgebra
![]() $(C,\gamma )$
, the dual linear map
$(C,\gamma )$
, the dual linear map
![]() $\gamma ^*:\ C^*\longrightarrow k$
to the coaugmentation
$\gamma ^*:\ C^*\longrightarrow k$
to the coaugmentation
![]() $\gamma :\ k\longrightarrow C$
defines an augmentation on the algebra
$\gamma :\ k\longrightarrow C$
defines an augmentation on the algebra
![]() $C^*$
. Accordingly, the one-dimensional vector space
$C^*$
. Accordingly, the one-dimensional vector space
![]() $k$
can be endowed with left and right
$k$
can be endowed with left and right
![]() $C^*$
-module structures provided by the augmentation
$C^*$
-module structures provided by the augmentation
![]() $\gamma ^*$
. These
$\gamma ^*$
. These
![]() $C^*$
-module structures on
$C^*$
-module structures on
![]() $k$
can be also viewed as coming from the left and right
$k$
can be also viewed as coming from the left and right
![]() $C$
-comodule structures on
$C$
-comodule structures on
![]() $k$
induced by the coaugmentation
$k$
induced by the coaugmentation
![]() $\gamma$
. The same module structures also come from the left and right
$\gamma$
. The same module structures also come from the left and right
![]() $C$
-contramodule structures on
$C$
-contramodule structures on
![]() $k$
induced by
$k$
induced by
![]() $\gamma$
.
$\gamma$
.
We start with a discussion of the case
![]() $n=1$
in Theorem6.1.
$n=1$
in Theorem6.1.
Proposition 6.3.
Let
![]() $C$
be a conilpotent coalgebra over a field
$C$
be a conilpotent coalgebra over a field
![]() $k$
. Then there is a natural
$k$
. Then there is a natural
![]() $k$
-vector space monomorphism
$k$
-vector space monomorphism
The dimension cardinality of the vector space
![]() $\textrm {Ext}_{C^*}^1(k,k)$
is equal to that of the vector space
$\textrm {Ext}_{C^*}^1(k,k)$
is equal to that of the vector space
![]() $\textrm {Ext}_C^1(k,k)^{**}$
.
$\textrm {Ext}_C^1(k,k)^{**}$
.
Proof.
Notice first of all the isomorphism
![]() $\textrm {Ext}_{C^{\mathrm{op}}}^*(k,k)\simeq \textrm {Ext}_C^*(k,k)$
provided by Proposition 4.1. Furthermore, let
$\textrm {Ext}_{C^{\mathrm{op}}}^*(k,k)\simeq \textrm {Ext}_C^*(k,k)$
provided by Proposition 4.1. Furthermore, let
![]() $A$
be an augmented
$A$
be an augmented
![]() $k$
-algebra with an augmentation
$k$
-algebra with an augmentation
![]() $\alpha :\ A\longrightarrow k$
and the augmentation ideal
$\alpha :\ A\longrightarrow k$
and the augmentation ideal
![]() $A_+=\ker (\alpha )\subset A$
. Then the vector space
$A_+=\ker (\alpha )\subset A$
. Then the vector space
![]() $\textrm {Ext}^1_A(k,k)\simeq \textrm {Tor}_1^A(k,k)^*\simeq \textrm {Ext}^1_{A^{\mathrm{op}}}(k,k)$
is computed as the kernel of the
$\textrm {Ext}^1_A(k,k)\simeq \textrm {Tor}_1^A(k,k)^*\simeq \textrm {Ext}^1_{A^{\mathrm{op}}}(k,k)$
is computed as the kernel of the
![]() $k$
-linear map
$k$
-linear map
dual to the multiplication map
![]() $A_+\otimes _k A_+\longrightarrow A_+$
. In particular, the vector space
$A_+\otimes _k A_+\longrightarrow A_+$
. In particular, the vector space
![]() $\textrm {Ext}^1_{C^*}(k,k)$
is naturally isomorphic to the kernel of the map
$\textrm {Ext}^1_{C^*}(k,k)$
is naturally isomorphic to the kernel of the map
dual to the multiplication map
![]() $C_+^*\otimes _k C_+^*\longrightarrow C_+^*$
(where
$C_+^*\otimes _k C_+^*\longrightarrow C_+^*$
(where
![]() $C_+=C/\gamma (k)$
).
$C_+=C/\gamma (k)$
).
On the other hand, from the cobar complex (6) one can immediately see that the vector space
![]() $\textrm {Ext}_C^1(k,k)$
is naturally isomorphic to the kernel of the comultiplication map
$\textrm {Ext}_C^1(k,k)$
is naturally isomorphic to the kernel of the comultiplication map
Hence, the double dual vector space
![]() $\textrm {Ext}_C^1(k,k)^{**}$
is naturally isomorphic to the kernel of the map
$\textrm {Ext}_C^1(k,k)^{**}$
is naturally isomorphic to the kernel of the map
Notice that
![]() $(C_+^*\otimes _kC_+^*)$
is naturally a subspace in
$(C_+^*\otimes _kC_+^*)$
is naturally a subspace in
![]() $(C_+\otimes _kC_+)^*$
; hence
$(C_+\otimes _kC_+)^*$
; hence
![]() $(C_+^*\otimes _kC_+^*)^*$
is a quotient space of
$(C_+^*\otimes _kC_+^*)^*$
is a quotient space of
![]() $(C_+\otimes _kC_+)^{**}$
. One can also observe that the cokernel of the map
$(C_+\otimes _kC_+)^{**}$
. One can also observe that the cokernel of the map
![]() $(C_+\otimes _kC_+)^* \longrightarrow C_+^*$
is naturally a quotient space of the cokernel of the map
$(C_+\otimes _kC_+)^* \longrightarrow C_+^*$
is naturally a quotient space of the cokernel of the map
![]() $C_+^*\otimes _kC_+^*\longrightarrow C_+^*$
. Comparing the maps (19) and (20), one immediately obtains the desired monomorphism (18).
$C_+^*\otimes _kC_+^*\longrightarrow C_+^*$
. Comparing the maps (19) and (20), one immediately obtains the desired monomorphism (18).
To compute the dimension cardinality, put
![]() $V=\textrm {Ext}^1_C(k,k)$
, and notice that
$V=\textrm {Ext}^1_C(k,k)$
, and notice that
![]() $C$
is a subcoalgebra of the cofree conilpotent (tensor) coalgebra
$C$
is a subcoalgebra of the cofree conilpotent (tensor) coalgebra
![]() $\textrm {Ten}(V)=\bigoplus _{n=0}^\infty V^{\otimes n}$
cospanned by
$\textrm {Ten}(V)=\bigoplus _{n=0}^\infty V^{\otimes n}$
cospanned by
![]() $V$
[Reference Positselski26, Lemma 5.2] (see [Reference Positselski36, Sections 2.3 and 3.3] for an introductory discussion). Hence, if
$V$
[Reference Positselski26, Lemma 5.2] (see [Reference Positselski36, Sections 2.3 and 3.3] for an introductory discussion). Hence, if
![]() $V$
is infinite-dimensional, then the dimension cardinalities of
$V$
is infinite-dimensional, then the dimension cardinalities of
![]() $V$
and
$V$
and
![]() $C_+$
are equal to each other. Now
$C_+$
are equal to each other. Now
![]() $V^{**}$
is a subspace in
$V^{**}$
is a subspace in
![]() $\textrm {Ext}^1_{C^*}(k,k)$
, which is in turn a subspace in
$\textrm {Ext}^1_{C^*}(k,k)$
, which is in turn a subspace in
![]() $C_+^{**}$
. Thus, the dimension cardinalities of all the three vector spaces
$C_+^{**}$
. Thus, the dimension cardinalities of all the three vector spaces
![]() $V^{**}$
,
$V^{**}$
,
![]() $\textrm {Ext}^1_{C^*}(k,k)$
, and
$\textrm {Ext}^1_{C^*}(k,k)$
, and
![]() $C_+^{**}$
are equal to each other. If
$C_+^{**}$
are equal to each other. If
![]() $V$
is finite-dimensional, then the map (18) is an isomorphism by Theorem5.1 (for
$V$
is finite-dimensional, then the map (18) is an isomorphism by Theorem5.1 (for
![]() $n=1$
).
$n=1$
).
Example 6.4.
Let
![]() $C$
be an infinitely cogenerated conilpotent coalgebra. Interpreted in the light of Lemma A.3 from the appendix, Proposition 6.3 tells us that there exists a short exact sequence of left
$C$
be an infinitely cogenerated conilpotent coalgebra. Interpreted in the light of Lemma A.3 from the appendix, Proposition 6.3 tells us that there exists a short exact sequence of left
![]() $C^*$
-modules
$C^*$
-modules
with the two-dimensional
![]() $C^*$
-module
$C^*$
-module
![]() $M$
not coming from any
$M$
not coming from any
![]() $C$
-comodule (while the one-dimensional
$C$
-comodule (while the one-dimensional
![]() $C^*$
-module
$C^*$
-module
![]() $k$
, of course, comes from the one-dimensional
$k$
, of course, comes from the one-dimensional
![]() $C$
-comodule
$C$
-comodule
![]() $k$
) via the comodule inclusion functor
$k$
) via the comodule inclusion functor
![]() $\Upsilon$
. Let us explain how to construct a short exact sequence (21) explicitly.
$\Upsilon$
. Let us explain how to construct a short exact sequence (21) explicitly.
Let
![]() $C$
be a conilpotent coalgebra. Recall the notation
$C$
be a conilpotent coalgebra. Recall the notation
![]() $F_0C=\gamma (k)$
and
$F_0C=\gamma (k)$
and
![]() $F_1C=\ker (C\to C_+\otimes _kC_+)$
from Section
5
. Then we have a natural direct sum decomposition
$F_1C=\ker (C\to C_+\otimes _kC_+)$
from Section
5
. Then we have a natural direct sum decomposition
![]() $F_1C=F_0C\oplus V$
, where
$F_1C=F_0C\oplus V$
, where
![]() $V=\ker (C_+\to C_+\otimes _kC_+)=\textrm {Ext}^1_C(k,k)$
. Choose a linear function
$V=\ker (C_+\to C_+\otimes _kC_+)=\textrm {Ext}^1_C(k,k)$
. Choose a linear function
![]() $f:\ V^*\longrightarrow k$
. The composition of linear maps
$f:\ V^*\longrightarrow k$
. The composition of linear maps
![]() $C^*\twoheadrightarrow (F_1C)^* \twoheadrightarrow V^*\overset f\longrightarrow k$
defines a linear function
$C^*\twoheadrightarrow (F_1C)^* \twoheadrightarrow V^*\overset f\longrightarrow k$
defines a linear function
![]() $\tilde f:\ C^*\longrightarrow k$
.
$\tilde f:\ C^*\longrightarrow k$
.
Let
![]() $M$
be the two-dimensional
$M$
be the two-dimensional
![]() $k$
-vector space with the basis vectors
$k$
-vector space with the basis vectors
![]() $e_1$
and
$e_1$
and
![]() $e_2$
. Define the left action of
$e_2$
. Define the left action of
![]() $C^*$
in
$C^*$
in
![]() $M$
by the formulas
$M$
by the formulas
![]() $ae_1=\gamma ^*(a)e_1$
and
$ae_1=\gamma ^*(a)e_1$
and
![]() $ae_2=\gamma ^*(a)e_2+\tilde f(a)e_1$
for all
$ae_2=\gamma ^*(a)e_2+\tilde f(a)e_1$
for all
![]() $a\in C^*$
(where
$a\in C^*$
(where
![]() $\gamma ^*:C^*\longrightarrow k$
is the dual map to the coaugmentation
$\gamma ^*:C^*\longrightarrow k$
is the dual map to the coaugmentation
![]() $\gamma$
). Then
$\gamma$
). Then
![]() $ke_1\subset M$
is a
$ke_1\subset M$
is a
![]() $C^*$
-submodule of
$C^*$
-submodule of
![]() $M$
isomorphic to
$M$
isomorphic to
![]() $\Upsilon (k)$
and
$\Upsilon (k)$
and
![]() $M/ke_1$
is a quotient module of
$M/ke_1$
is a quotient module of
![]() $M$
also isomorphic to
$M$
also isomorphic to
![]() $\Upsilon (k)$
. The
$\Upsilon (k)$
. The
![]() $C^*$
-module
$C^*$
-module
![]() $M$
itself belongs to the essential image of the functor
$M$
itself belongs to the essential image of the functor
![]() $\Upsilon$
if and only if the linear function
$\Upsilon$
if and only if the linear function
![]() $f:\ V^*\longrightarrow k$
comes from a vector in
$f:\ V^*\longrightarrow k$
comes from a vector in
![]() $V$
.
$V$
.
Before passing to the case
![]() $n\gt 1$
in Theorem6.1, we need a preparatory lemma.
$n\gt 1$
in Theorem6.1, we need a preparatory lemma.
Lemma 6.5.
Let
![]() $(C,\gamma )$
be a coaugmented coalgebra over
$(C,\gamma )$
be a coaugmented coalgebra over
![]() $k$
and
$k$
and
![]() $N$
be a right
$N$
be a right
![]() $C$
-comodule. Then there is a natural monomorphism of
$C$
-comodule. Then there is a natural monomorphism of
![]() $k$
-vector spaces
$k$
-vector spaces
from the double dual vector space to the vector subspace
![]() $N_\gamma \subset N$
to the vector space of left
$N_\gamma \subset N$
to the vector space of left
![]() $C^*$
-module morphisms
$C^*$
-module morphisms
![]() $N^*\longrightarrow k$
. The map
$N^*\longrightarrow k$
. The map
![]() $\xi _N$
is an isomorphism whenever the coalgebra
$\xi _N$
is an isomorphism whenever the coalgebra
![]() $C$
is conilpotent and finitely cogenerated.
$C$
is conilpotent and finitely cogenerated.
Proof.
The inclusion
![]() $N_\gamma \longrightarrow N$
is a morphism of right
$N_\gamma \longrightarrow N$
is a morphism of right
![]() $C$
-comodules. Consequently, the
$C$
-comodules. Consequently, the
![]() $k$
-vector space dual map
$k$
-vector space dual map
![]() $N^*\longrightarrow (N_\gamma )^*$
is an epimorphism of left
$N^*\longrightarrow (N_\gamma )^*$
is an epimorphism of left
![]() $C^*$
-modules (and in fact, of left
$C^*$
-modules (and in fact, of left
![]() $C$
-contramodules), where the
$C$
-contramodules), where the
![]() $C^*$
-module (or
$C^*$
-module (or
![]() $C$
-contramodule) structure on
$C$
-contramodule) structure on
![]() $(N_\gamma )^*$
is induced by the (co)augmentation. Applying the functor
$(N_\gamma )^*$
is induced by the (co)augmentation. Applying the functor
![]() $\textrm {Hom}_{C^*}({-},k)$
, we obtain the desired injective map of
$\textrm {Hom}_{C^*}({-},k)$
, we obtain the desired injective map of
![]() $k$
-vector spaces
$k$
-vector spaces
If the coalgebra
![]() $C$
is conilpotent and finitely cogenerated, then the contramodule forgetful functor
$C$
is conilpotent and finitely cogenerated, then the contramodule forgetful functor
![]() $C{{-\mathsf{Contra}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
from the category of left
$C{{-\mathsf{Contra}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
from the category of left
![]() $C$
-contramodules to the category of left
$C$
-contramodules to the category of left
![]() $C^*$
-modules is fully faithful [Reference Positselski30, Theorem 2.1] (see Theorem7.4 below). Consequently, we have
$C^*$
-modules is fully faithful [Reference Positselski30, Theorem 2.1] (see Theorem7.4 below). Consequently, we have
![]() $\textrm {Hom}_{C^*}(N^*,k)=\textrm {Hom}^C(N^*,k)$
.
$\textrm {Hom}_{C^*}(N^*,k)=\textrm {Hom}^C(N^*,k)$
.
It remains to observe that the natural map
is an isomorphism for any coaugmented coalgebra
![]() $(C,\gamma )$
. Indeed, we have
$(C,\gamma )$
. Indeed, we have
because
![]() ${}^\gamma (N^*)\simeq (N_\gamma )^*$
. The latter isomorphism is a particular case of the formula (4) in Section 3. Alternatively, one can obtain the isomorphism (22) as a particular case of the isomorphism (7) from Lemma 4.2 for
${}^\gamma (N^*)\simeq (N_\gamma )^*$
. The latter isomorphism is a particular case of the formula (4) in Section 3. Alternatively, one can obtain the isomorphism (22) as a particular case of the isomorphism (7) from Lemma 4.2 for
![]() $L=k$
and
$L=k$
and
![]() $M=N$
.
$M=N$
.
Proposition 6.6.
Let
![]() $C$
be a finitely cogenerated conilpotent coalgebra over a field
$C$
be a finitely cogenerated conilpotent coalgebra over a field
![]() $k$
and
$k$
and
![]() $n\ge 2$
an integer such that the vector space
$n\ge 2$
an integer such that the vector space
![]() $\textrm {Ext}^i_C(k,k)$
is finite-dimensional for all
$\textrm {Ext}^i_C(k,k)$
is finite-dimensional for all
![]() $1\le i\le n-1$
. Then there is a natural
$1\le i\le n-1$
. Then there is a natural
![]() $k$
-vector space isomorphism
$k$
-vector space isomorphism
Proof.
Similarly to the proof of Theorem5.1, we consider a minimal injective/cofree coresolution (14) of the right
![]() $C$
-comodule
$C$
-comodule
![]() $k$
. The assumption of the proposition implies that the vector spaces
$k$
. The assumption of the proposition implies that the vector spaces
![]() $V_i\simeq \textrm {Ext}^i_C(k,k)$
are finite-dimensional for all
$V_i\simeq \textrm {Ext}^i_C(k,k)$
are finite-dimensional for all
![]() $0\le i\le n-1$
. Applying the dual vector space functor
$0\le i\le n-1$
. Applying the dual vector space functor
![]() $\textrm {Hom}_k({-},k)$
to the complex (14), we obtain a resolution of the left
$\textrm {Hom}_k({-},k)$
to the complex (14), we obtain a resolution of the left
![]() $C^*$
-module
$C^*$
-module
![]() $k$
,
$k$
,
(cf. formula (15), which holds under the stricter assumptions of Theorem5.1).
Lemma A.1 from the appendix tells us that, for every
![]() $0\le i\le n$
and any left
$0\le i\le n$
and any left
![]() $C^*$
-module
$C^*$
-module
![]() $M$
, the space
$M$
, the space
![]() $\textrm {Ext}^i_{C^*}(k,M)$
can be computed as the degree
$\textrm {Ext}^i_{C^*}(k,M)$
can be computed as the degree
![]() $i$
cohomology space of the complex obtained by applying the functor
$i$
cohomology space of the complex obtained by applying the functor
![]() $\textrm {Hom}_{C^*}({-},M)$
to the resolution (24) of the left
$\textrm {Hom}_{C^*}({-},M)$
to the resolution (24) of the left
![]() $C^*$
-module
$C^*$
-module
![]() $k$
. For
$k$
. For
![]() $M=k$
, the resulting complex turns into
$M=k$
, the resulting complex turns into
By Lemma 6.5, the complex (25) is naturally isomorphic to the complex
obtained by applying the functor
![]() $(({-})_\gamma )^{**}$
to the coresolution (14). As the latter coresolution was chosen to be minimal, the differential in the complex (26) (or, which is the same, in the complex (25)) vanishes. Thus,
$(({-})_\gamma )^{**}$
to the coresolution (14). As the latter coresolution was chosen to be minimal, the differential in the complex (26) (or, which is the same, in the complex (25)) vanishes. Thus,
![]() $\textrm {Ext}^n_{C^*}(k,k)\simeq V_n^{**}\simeq \textrm {Ext}^n_C(k,k)^{**}$
.
$\textrm {Ext}^n_{C^*}(k,k)\simeq V_n^{**}\simeq \textrm {Ext}^n_C(k,k)^{**}$
.
This proves existence of an isomorphism (23). To show that this isomorphism is natural, consider an arbitrary injective coresolution
of the right
![]() $C$
-comodule
$C$
-comodule
![]() $k$
. Then
$k$
. Then
is a (nonprojective) resolution of the left
![]() $C^*$
-module
$C^*$
-module
![]() $k$
. However, the coresolution (27) is homotopy equivalent (as a complex of injective right
$k$
. However, the coresolution (27) is homotopy equivalent (as a complex of injective right
![]() $C$
-comodules) to the minimal coresolution (14). Hence, the resolution (28) is homotopy equivalent (as a complex of left
$C$
-comodules) to the minimal coresolution (14). Hence, the resolution (28) is homotopy equivalent (as a complex of left
![]() $C^*$
-modules) to the initially projective resolution (24). Consequently, the natural map (47) from Lemma A.1 for the nonprojective resolution (28) is naturally isomorphic to the similar map for the initially projective resolution (24).
$C^*$
-modules) to the initially projective resolution (24). Consequently, the natural map (47) from Lemma A.1 for the nonprojective resolution (28) is naturally isomorphic to the similar map for the initially projective resolution (24).
Thus, one can compute
![]() $\textrm {Ext}^i_{C^*}(k,k)$
for
$\textrm {Ext}^i_{C^*}(k,k)$
for
![]() $0\le i\le n$
using the nonprojective resolution (28), obtaining natural isomorphisms
$0\le i\le n$
using the nonprojective resolution (28), obtaining natural isomorphisms
(with the second isomorphism provided by Lemma 6.5) for all
![]() $0\le i\le n$
.
$0\le i\le n$
.
Proof of Theorem
6.1. The map
![]() $\textrm {Ext}^n_C(L,M)\longrightarrow \textrm {Ext}^n_{C^*}(L,M)$
is injective for all left
$\textrm {Ext}^n_C(L,M)\longrightarrow \textrm {Ext}^n_{C^*}(L,M)$
is injective for all left
![]() $C$
-comodules
$C$
-comodules
![]() $L$
and
$L$
and
![]() $M$
in our assumptions by Corollary 5.3. The dimension cardinality assertion of the theorem is provided by Proposition 6.3 (for
$M$
in our assumptions by Corollary 5.3. The dimension cardinality assertion of the theorem is provided by Proposition 6.3 (for
![]() $n=1$
) or Proposition 6.6 (for
$n=1$
) or Proposition 6.6 (for
![]() $n\ge 2$
) together with Lemma 6.2. The nonsurjectivity assertion follows from the dimension inequality.
$n\ge 2$
) together with Lemma 6.2. The nonsurjectivity assertion follows from the dimension inequality.
Remark 6.7. Arguing more carefully, one can show that, in the assumptions of Proposition 6.6, the isomorphism (23) identifies the map
![]() $\textrm {Ext}^n_C(k,k)\longrightarrow \textrm {Ext}^n_{C^*}(k,k)$
induced by the comodule inclusion functor
$\textrm {Ext}^n_C(k,k)\longrightarrow \textrm {Ext}^n_{C^*}(k,k)$
induced by the comodule inclusion functor
![]() $\Upsilon :\ C{{-\mathsf{Comod}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
with the natural inclusion
$\Upsilon :\ C{{-\mathsf{Comod}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
with the natural inclusion
![]() $\textrm {Ext}^n_C(k,k)\longrightarrow \textrm {Ext}^n_{C^*}(k,k)^{**}$
of a vector space
$\textrm {Ext}^n_C(k,k)\longrightarrow \textrm {Ext}^n_{C^*}(k,k)^{**}$
of a vector space
![]() $\textrm {Ext}^n_C(k,k)$
into its double dual vector space. For this purpose, one can start with comparing the proofs of Propositions 4.3 and 6.6 in order to observe that the forgetful functor
$\textrm {Ext}^n_C(k,k)$
into its double dual vector space. For this purpose, one can start with comparing the proofs of Propositions 4.3 and 6.6 in order to observe that the forgetful functor
![]() $\Theta :\ C{{-\mathsf{Contra}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
induces an isomorphism
$\Theta :\ C{{-\mathsf{Contra}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
induces an isomorphism
![]() $\textrm {Ext}^{C,n}(k,k)\simeq \textrm {Ext}_{C^*}^n(k,k)$
in the assumptions of Proposition 6.6. Then the result of Proposition 4.3 identifies the map
$\textrm {Ext}^{C,n}(k,k)\simeq \textrm {Ext}_{C^*}^n(k,k)$
in the assumptions of Proposition 6.6. Then the result of Proposition 4.3 identifies the map
![]() $\textrm {Ext}^n_{C^{\mathrm{op}}}(k,k)\longrightarrow \textrm {Ext}^n_{C^*}(k,k)$
induced by the dual vector space functor
$\textrm {Ext}^n_{C^{\mathrm{op}}}(k,k)\longrightarrow \textrm {Ext}^n_{C^*}(k,k)$
induced by the dual vector space functor
![]() $N\longmapsto N^*:\ {{\mathsf{Comod}-}} C\longrightarrow C^*{{-\mathsf{Mod}}}$
with the natural inclusion
$N\longmapsto N^*:\ {{\mathsf{Comod}-}} C\longrightarrow C^*{{-\mathsf{Mod}}}$
with the natural inclusion
![]() $\textrm {Ext}^n_{C^{\mathrm{op}}}(k,k)\longrightarrow \textrm {Ext}^n_{C^{\mathrm{op}}}(k,k)^{**}$
. It remains to restrict the consideration to finite-dimensional comodules and use the observations from the second proof of Proposition 4.1.
$\textrm {Ext}^n_{C^{\mathrm{op}}}(k,k)\longrightarrow \textrm {Ext}^n_{C^{\mathrm{op}}}(k,k)^{**}$
. It remains to restrict the consideration to finite-dimensional comodules and use the observations from the second proof of Proposition 4.1.
7. Weakly finite Koszulity implies contramodule Ext isomorphism
Before stating the main theorem of this section, let us have a discussion of separated and nonseparated contramodules.
Let
![]() $C=(C,\gamma )$
be a coaugmented coalgebra and
$C=(C,\gamma )$
be a coaugmented coalgebra and
![]() $P$
be a left
$P$
be a left
![]() $C$
-contramodule. For every
$C$
-contramodule. For every
![]() $m\ge 0$
, denote by
$m\ge 0$
, denote by
![]() $F^mP\subset P$
the image of the subspace
$F^mP\subset P$
the image of the subspace
![]() $\textrm {Hom}_k(C/F_{m-1}C,P)\subset \textrm {Hom}_k(C,P)$
under the contraaction map
$\textrm {Hom}_k(C/F_{m-1}C,P)\subset \textrm {Hom}_k(C,P)$
under the contraaction map
![]() $\pi :\ \textrm {Hom}_k(C,P)\longrightarrow P$
. So one has
$\pi :\ \textrm {Hom}_k(C,P)\longrightarrow P$
. So one has
![]() $F^0P=P$
and
$F^0P=P$
and
![]() $F^1P=\ker (P\twoheadrightarrow {}^\gamma \!P)$
(in the notation of Sections 3 and 5). One can check that
$F^1P=\ker (P\twoheadrightarrow {}^\gamma \!P)$
(in the notation of Sections 3 and 5). One can check that
![]() $F$
is a contramultiplicative decreasing filtration on
$F$
is a contramultiplicative decreasing filtration on
![]() $P$
compatible with the increasing filtration
$P$
compatible with the increasing filtration
![]() $F$
on
$F$
on
![]() $C$
, that is
$C$
, that is
for all
![]() $p$
,
$p$
,
![]() $q\ge 0$
.
$q\ge 0$
.
In other words, this means that
![]() $F^mP$
is a
$F^mP$
is a
![]() $C$
-subcontramodule of
$C$
-subcontramodule of
![]() $P$
for every
$P$
for every
![]() $m\ge 0$
and the successive quotient
$m\ge 0$
and the successive quotient
![]() $C$
-contramodules
$C$
-contramodules
![]() $F^mP/F^{m+1}P$
are trivial (i.e., the contraaction of
$F^mP/F^{m+1}P$
are trivial (i.e., the contraaction of
![]() $C$
in them is induced by the coaugmentation
$C$
in them is induced by the coaugmentation
![]() $\gamma$
). In fact, one has
$\gamma$
). In fact, one has
![]() $F^mP/F^{m+1}P={}^\gamma (F^mP)$
for every
$F^mP/F^{m+1}P={}^\gamma (F^mP)$
for every
![]() $m\ge 0$
.
$m\ge 0$
.
The problem with the decreasing filtration
![]() $F$
on
$F$
on
![]() $P$
is that it is not in general separated (not even when
$P$
is that it is not in general separated (not even when
![]() $C$
is a conilpotent coalgebra); see the counterexample in [Reference Positselski24, Section 1.5] (going back to [Reference Simon42, Example 2.5], [Reference Yekutieli48, Example 3.20], and [Reference Positselski20, Section A.1.1]). The next lemma explains how this problem can be partially rectified (for a conilpotent coalgebra
$C$
is a conilpotent coalgebra); see the counterexample in [Reference Positselski24, Section 1.5] (going back to [Reference Simon42, Example 2.5], [Reference Yekutieli48, Example 3.20], and [Reference Positselski20, Section A.1.1]). The next lemma explains how this problem can be partially rectified (for a conilpotent coalgebra
![]() $C$
).
$C$
).
We say that a vector space
![]() $P$
endowed with a decreasing filtration
$P$
endowed with a decreasing filtration
![]() $F$
is separated if the natural map to the projective limit
$F$
is separated if the natural map to the projective limit
is injective, and that
![]() $P$
is complete if the map
$P$
is complete if the map
![]() $\lambda _{P,F}$
is surjective. A contramodule
$\lambda _{P,F}$
is surjective. A contramodule
![]() $P$
over a conilpotent coalgebra
$P$
over a conilpotent coalgebra
![]() $C$
is said to be separated (respectively, complete) if it is separated (resp., complete) with respect to its natural decreasing filtration
$C$
is said to be separated (respectively, complete) if it is separated (resp., complete) with respect to its natural decreasing filtration
![]() $F$
constructed above.
$F$
constructed above.
Notice that, for any subcontramodule
![]() $Q$
in a contramodule
$Q$
in a contramodule
![]() $P$
, one has
$P$
, one has
![]() $F^mQ\subset F^mP$
for all
$F^mQ\subset F^mP$
for all
![]() $m\ge 0$
. Thus, any subcontramodule of a separated contramodule is separated. For a free contramodule
$m\ge 0$
. Thus, any subcontramodule of a separated contramodule is separated. For a free contramodule
![]() $P=\textrm {Hom}_k(C,V)$
, one has
$P=\textrm {Hom}_k(C,V)$
, one has
![]() $F^mP=\textrm {Hom}_k(C/F_{m-1}C,V)$
. Hence, all free (and therefore, all projective) contramodules over a conilpotent coalgebra are separated and complete.
$F^mP=\textrm {Hom}_k(C/F_{m-1}C,V)$
. Hence, all free (and therefore, all projective) contramodules over a conilpotent coalgebra are separated and complete.
Lemma 7.1.
Let
![]() $C$
be a conilpotent coalgebra. Then
$C$
be a conilpotent coalgebra. Then
(a) any
![]() $C$
-contramodule is complete;
$C$
-contramodule is complete;
(b) any
![]() $C$
-contramodule can be presented as the quotient contramodule of a separated contramodule by a separated subcontramodule.
$C$
-contramodule can be presented as the quotient contramodule of a separated contramodule by a separated subcontramodule.
Proof. Part (b) holds because any contramodule is a quotient of a free contramodule, which is separated, and any subcontramodule of a separated contramodule is separated. For part (a), see [Reference Positselski20, Lemma A.2.3].
The aim of this section is to prove the following theorem.
Theorem 7.2.
Let
![]() $C$
be a conilpotent coalgebra over a field
$C$
be a conilpotent coalgebra over a field
![]() $k$
and
$k$
and
![]() $n\ge 1$
be an integer such that the vector space
$n\ge 1$
be an integer such that the vector space
![]() $\textrm {Ext}^i_C(k,k)$
is finite-dimensional for all
$\textrm {Ext}^i_C(k,k)$
is finite-dimensional for all
![]() $1\le i\le n$
. Then the map of the Ext spaces
$1\le i\le n$
. Then the map of the Ext spaces
induced by the forgetful functor
![]() $\Theta :\ C{{-\mathsf{Contra}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
is an isomorphism for all left
$\Theta :\ C{{-\mathsf{Contra}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
is an isomorphism for all left
![]() $C$
-contramodules
$C$
-contramodules
![]() $P$
, all separated left
$P$
, all separated left
![]() $C$
-contramodules
$C$
-contramodules
![]() $Q$
, and all
$Q$
, and all
![]() $0\le i\le n-1$
. The map (29) is also an isomorphism for all left
$0\le i\le n-1$
. The map (29) is also an isomorphism for all left
![]() $C$
-contramodules
$C$
-contramodules
![]() $P$
and
$P$
and
![]() $Q$
and all
$Q$
and all
![]() $0\le i\le n-2$
.
$0\le i\le n-2$
.
The following lemma, describing some tensor products of
![]() $C^*$
-modules for a coalgebra
$C^*$
-modules for a coalgebra
![]() $C$
, is a partial dual version of Lemma 5.2.
$C$
, is a partial dual version of Lemma 5.2.
Lemma 7.3.
Let
![]() $C$
be a coalgebra over
$C$
be a coalgebra over
![]() $k$
, let
$k$
, let
![]() $N$
be a left
$N$
be a left
![]() $C$
-comodule, and let
$C$
-comodule, and let
![]() $U$
be a
$U$
be a
![]() $k$
-vector space. Then there is a natural map of
$k$
-vector space. Then there is a natural map of
![]() $k$
-vector spaces
$k$
-vector spaces
which is an isomorphism whenever
![]() $N$
is a finitely cogenerated injective
$N$
is a finitely cogenerated injective
![]() $C$
-comodule. Here, the left
$C$
-comodule. Here, the left
![]() $C^*$
-module structure on
$C^*$
-module structure on
![]() $\textrm {Hom}_k(C,U)$
comes from the free left
$\textrm {Hom}_k(C,U)$
comes from the free left
![]() $C$
-contramodule structure, or equivalently, is induced by the right
$C$
-contramodule structure, or equivalently, is induced by the right
![]() $C^*$
-module structure on
$C^*$
-module structure on
![]() $C$
(coming from the right
$C$
(coming from the right
![]() $C$
-comodule structure on
$C$
-comodule structure on
![]() $C$
).
$C$
).
Proof.
The map
![]() $\zeta _{N,U}$
is defined by the formula
$\zeta _{N,U}$
is defined by the formula
for all
![]() $f\in N^*$
,
$f\in N^*$
,
![]() $g\in \textrm {Hom}_k(C,U)$
, and
$g\in \textrm {Hom}_k(C,U)$
, and
![]() $x\in N$
. Here,
$x\in N$
. Here,
![]() $\nu (x)=x_{(-1)}\otimes x_{(0)}\in C\otimes _k N$
is a notation for the left
$\nu (x)=x_{(-1)}\otimes x_{(0)}\in C\otimes _k N$
is a notation for the left
![]() $C$
-coaction map
$C$
-coaction map
![]() $\nu :\ N\longrightarrow C\otimes _k N$
. So
$\nu :\ N\longrightarrow C\otimes _k N$
. So
![]() $f(x_{(0)})\in k$
and
$f(x_{(0)})\in k$
and
![]() $g(x_{(-1)})\in U$
.
$g(x_{(-1)})\in U$
.
To prove the isomorphism assertion for a finitely cogenerated injective
![]() $C$
-comodule
$C$
-comodule
![]() $N$
, it suffices to consider the case
$N$
, it suffices to consider the case
![]() $N=C\otimes _kV$
, where
$N=C\otimes _kV$
, where
![]() $\dim _kV\lt \infty$
. In this case,
$\dim _kV\lt \infty$
. In this case,
![]() $N^*=V^*\otimes _k C^*$
is a free right
$N^*=V^*\otimes _k C^*$
is a free right
![]() $C^*$
-module, so
$C^*$
-module, so
![]() $N^*\otimes _{C^*}\textrm {Hom}_k(C,U)=V^*\otimes _k\textrm {Hom}_k(C,U)=\textrm {Hom}_k(V,\textrm {Hom}_k(C,U)) =\textrm {Hom}_k(C\otimes _kV,\ U)$
.
$N^*\otimes _{C^*}\textrm {Hom}_k(C,U)=V^*\otimes _k\textrm {Hom}_k(C,U)=\textrm {Hom}_k(V,\textrm {Hom}_k(C,U)) =\textrm {Hom}_k(C\otimes _kV,\ U)$
.
The most difficult part of the proof of Theorem7.2 is the case of
![]() $n=1$
. This is a previously known result [Reference Positselski30]. Notice that, according to the following theorem, no separatedness assumptions are needed in Theorem7.2 for
$n=1$
. This is a previously known result [Reference Positselski30]. Notice that, according to the following theorem, no separatedness assumptions are needed in Theorem7.2 for
![]() $n=1$
.
$n=1$
.
Theorem 7.4.
Let
![]() $C$
be a finitely cogenerated conilpotent coalgebra over a field
$C$
be a finitely cogenerated conilpotent coalgebra over a field
![]() $k$
. Then the contramodule forgetful functor
$k$
. Then the contramodule forgetful functor
![]() $\Theta :\ C{{-\mathsf{Contra}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
is fully faithful.
$\Theta :\ C{{-\mathsf{Contra}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
is fully faithful.
Proof.
Moreover, the forgetful functor
![]() $C{{-\mathsf{Contra}}}\longrightarrow R{{-\mathsf{Mod}}}$
(defined as the composition
$C{{-\mathsf{Contra}}}\longrightarrow R{{-\mathsf{Mod}}}$
(defined as the composition
![]() $C{{-\mathsf{Contra}}}\longrightarrow C^*{{-\mathsf{Mod}}}\longrightarrow R{{-\mathsf{Mod}}}$
) is fully faithful for any dense subring
$C{{-\mathsf{Contra}}}\longrightarrow C^*{{-\mathsf{Mod}}}\longrightarrow R{{-\mathsf{Mod}}}$
) is fully faithful for any dense subring
![]() $R\subset C^*$
in the natural pro-finite-dimensional (otherwise known as linearly compact or pseudocompact) topology of the
$R\subset C^*$
in the natural pro-finite-dimensional (otherwise known as linearly compact or pseudocompact) topology of the
![]() $k$
-algebra
$k$
-algebra
![]() $C^*$
. See [Reference Positselski30, Theorem 2.1]. For a discussion of related results with further references, see [Reference Positselski24, Section 3.8].
$C^*$
. See [Reference Positselski30, Theorem 2.1]. For a discussion of related results with further references, see [Reference Positselski24, Section 3.8].
Proof of Theorem
7.2. The argument resembles the proofs of the contramodule Ext comparison theorems in [Reference Positselski35, Sections 5.4 and 5.7] (see specifically [Reference Positselski35, Theorem 5.20]). Notice first of all that the coalgebra
![]() $C$
is finitely cogenerated in the assumptions of Theorem7.2, so the functor
$C$
is finitely cogenerated in the assumptions of Theorem7.2, so the functor
![]() $\Theta$
is fully faithful by Theorem7.4.
$\Theta$
is fully faithful by Theorem7.4.
To prove the first assertion of the theorem, let
![]() $Q$
be a separated left
$Q$
be a separated left
![]() $C$
-contramodule. According to Lemma A.6, it suffices to show that
$C$
-contramodule. According to Lemma A.6, it suffices to show that
![]() $\textrm {Ext}^i_{C^*}(P,Q)=0$
for all projective left
$\textrm {Ext}^i_{C^*}(P,Q)=0$
for all projective left
![]() $C$
-contramodules
$C$
-contramodules
![]() $P$
and all integers
$P$
and all integers
![]() $1\le i\le n-1$
.
$1\le i\le n-1$
.
Lemma 7.1(a) says that the
![]() $C$
-contramodule
$C$
-contramodule
![]() $Q$
is complete with respect to its natural decreasing filtration
$Q$
is complete with respect to its natural decreasing filtration
![]() $F$
; so it is separated and complete under our assumptions. According to the discussion preceding the lemma, the successive quotient contramodules
$F$
; so it is separated and complete under our assumptions. According to the discussion preceding the lemma, the successive quotient contramodules
![]() $F^mQ/F^{m-1}Q$
have trivial
$F^mQ/F^{m-1}Q$
have trivial
![]() $C$
-contramodule structures (i.e., their
$C$
-contramodule structures (i.e., their
![]() $C$
-contramodule structures are induced by the coaugmentation
$C$
-contramodule structures are induced by the coaugmentation
![]() $\gamma$
). Using the dual Eklof lemma [Reference Eklof and Trlifaj6, Proposition 18], the question reduces to showing that
$\gamma$
). Using the dual Eklof lemma [Reference Eklof and Trlifaj6, Proposition 18], the question reduces to showing that
![]() $\textrm {Ext}_{C^*}^i(P,T)=0$
for all
$\textrm {Ext}_{C^*}^i(P,T)=0$
for all
![]() $k$
-vector spaces
$k$
-vector spaces
![]() $T$
with trivial
$T$
with trivial
![]() $C$
-contramodule structures.
$C$
-contramodule structures.
Any vector space
![]() $T$
is a direct summand of the dual vector space
$T$
is a direct summand of the dual vector space
![]() $W^*$
to some vector space
$W^*$
to some vector space
![]() $W$
. Thus it suffices to show that the vector space
$W$
. Thus it suffices to show that the vector space
![]() $\textrm {Ext}_{C^*}^i(P,W^*)\simeq \textrm {Tor}^{C^*}_i(W,P)^*$
vanishes. Finally,
$\textrm {Ext}_{C^*}^i(P,W^*)\simeq \textrm {Tor}^{C^*}_i(W,P)^*$
vanishes. Finally,
![]() $W$
is a direct sum of copies of the one-dimensional vector space
$W$
is a direct sum of copies of the one-dimensional vector space
![]() $k$
, and Tor commutes with the direct sums. So we need to show that
$k$
, and Tor commutes with the direct sums. So we need to show that
![]() $\textrm {Tor}^{C^*}_i(k,P)=0$
for any projective left
$\textrm {Tor}^{C^*}_i(k,P)=0$
for any projective left
![]() $C$
-contramodule
$C$
-contramodule
![]() $P$
and
$P$
and
![]() $1\le i\le n-1$
(and the trivial right
$1\le i\le n-1$
(and the trivial right
![]() $C^*$
-module structure on
$C^*$
-module structure on
![]() $k$
). Equivalently, this means that the space
$k$
). Equivalently, this means that the space
![]() $\textrm {Tor}^{C^*}_i(k,\textrm {Hom}_k(C,U))$
should vanish for all
$\textrm {Tor}^{C^*}_i(k,\textrm {Hom}_k(C,U))$
should vanish for all
![]() $k$
-vector spaces
$k$
-vector spaces
![]() $U$
and
$U$
and
![]() $1\le i\le n-1$
.
$1\le i\le n-1$
.
This time, we consider a minimal injective/cofree coresolution of the left
![]() $C$
-comodule
$C$
-comodule
![]() $k$
,
$k$
,
and apply the dual vector space functor
![]() $\textrm {Hom}_k({-},k)$
to it in order to obtain an initially projective resolution of the right
$\textrm {Hom}_k({-},k)$
to it in order to obtain an initially projective resolution of the right
![]() $C^*$
-module
$C^*$
-module
![]() $k$
,
$k$
,
Here the vector space
![]() $V_i\simeq \textrm {Ext}_C^i(k,k)$
is finite-dimensional for
$V_i\simeq \textrm {Ext}_C^i(k,k)$
is finite-dimensional for
![]() $0\le i\le n$
by assumption. For every
$0\le i\le n$
by assumption. For every
![]() $0\le i\le n+1$
and any left
$0\le i\le n+1$
and any left
![]() $C^*$
-module
$C^*$
-module
![]() $P$
, the space
$P$
, the space
![]() $\textrm {Tor}^{C^*}_i(k,P)$
can be computed as the degree
$\textrm {Tor}^{C^*}_i(k,P)$
can be computed as the degree
![]() $i$
homology space of the complex obtained by applying the functor
$i$
homology space of the complex obtained by applying the functor
![]() ${-}\otimes _{C^*}P$
to the resolution (31) of the right
${-}\otimes _{C^*}P$
to the resolution (31) of the right
![]() $C^*$
-module
$C^*$
-module
![]() $k$
(see Lemma A.2). We are only interested in
$k$
(see Lemma A.2). We are only interested in
![]() $0\le i\le n-1$
now, so we only write down the resulting complex in the cohomological degrees from
$0\le i\le n-1$
now, so we only write down the resulting complex in the cohomological degrees from
![]() $0$
to
$0$
to
![]() $n$
. It has the form
$n$
. It has the form
which for
![]() $P=\textrm {Hom}_k(C,U)$
turns into
$P=\textrm {Hom}_k(C,U)$
turns into
By Lemma 7.3, the complex (32) (in the cohomological degrees
![]() $\le n$
) can be simply obtained by applying the contravariant vector space Hom functor
$\le n$
) can be simply obtained by applying the contravariant vector space Hom functor
![]() $\textrm {Hom}_k({-},U)$
to the coresolution (30). Consequently, the complex (32) is exact in the cohomological degrees
$\textrm {Hom}_k({-},U)$
to the coresolution (30). Consequently, the complex (32) is exact in the cohomological degrees
![]() $0\lt i\le n-1$
. Therefore,
$0\lt i\le n-1$
. Therefore,
![]() $\textrm {Tor}^{C^*}_i(k,\textrm {Hom}_k(C,U))=0$
for
$\textrm {Tor}^{C^*}_i(k,\textrm {Hom}_k(C,U))=0$
for
![]() $0\lt i\le n-1$
, as desired.
$0\lt i\le n-1$
, as desired.
Having proved the first assertion of the theorem, we can now easily deduce the second one. For a nonseparated left
![]() $C$
-contramodule
$C$
-contramodule
![]() $Y$
, by Lemma A.6 we only need to show that
$Y$
, by Lemma A.6 we only need to show that
![]() $\textrm {Ext}^i_{C^*}(P,Y)=0$
for all projective left
$\textrm {Ext}^i_{C^*}(P,Y)=0$
for all projective left
![]() $C$
-contramodules
$C$
-contramodules
![]() $P$
and
$P$
and
![]() $1\le i\le n-2$
. Lemma 7.1(b) provides a short exact sequence
$1\le i\le n-2$
. Lemma 7.1(b) provides a short exact sequence
![]() $0\longrightarrow Q'\longrightarrow Q''\longrightarrow Y\longrightarrow 0$
with separated
$0\longrightarrow Q'\longrightarrow Q''\longrightarrow Y\longrightarrow 0$
with separated
![]() $C$
-contramodules
$C$
-contramodules
![]() $Q'$
and
$Q'$
and
![]() $Q''$
. In the long exact sequence
$Q''$
. In the long exact sequence
![]() $\dotsb \longrightarrow \textrm {Ext}^i_{C^*}(P,Q'')\longrightarrow \textrm {Ext}^i_{C^*}(P,Y)\longrightarrow \textrm {Ext}^{i+1}_{C^*}(P,Q')\longrightarrow \dotsb$
, we have
$\dotsb \longrightarrow \textrm {Ext}^i_{C^*}(P,Q'')\longrightarrow \textrm {Ext}^i_{C^*}(P,Y)\longrightarrow \textrm {Ext}^{i+1}_{C^*}(P,Q')\longrightarrow \dotsb$
, we have
![]() $\textrm {Ext}^i_{C^*}(P,Q'')=0=\textrm {Ext}^{i+1}_{C^*}(P,Q')$
, hence
$\textrm {Ext}^i_{C^*}(P,Q'')=0=\textrm {Ext}^{i+1}_{C^*}(P,Q')$
, hence
![]() $\textrm {Ext}^i_{C^*}(P,Y)=0$
.
$\textrm {Ext}^i_{C^*}(P,Y)=0$
.
Corollary 7.5.
Let
![]() $C$
be a conilpotent coalgebra over a field
$C$
be a conilpotent coalgebra over a field
![]() $k$
and
$k$
and
![]() $n\ge 0$
be an integer such that the vector space
$n\ge 0$
be an integer such that the vector space
![]() $\textrm {Ext}_C^i(k,k)$
is finite-dimensional for all
$\textrm {Ext}_C^i(k,k)$
is finite-dimensional for all
![]() $1\le i\le n$
. Then the map of the Ext spaces
$1\le i\le n$
. Then the map of the Ext spaces
induced by the forgetful functor
![]() $\Theta :\ C{{-\mathsf{Contra}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
is injective for all left
$\Theta :\ C{{-\mathsf{Contra}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
is injective for all left
![]() $C$
-contramodules
$C$
-contramodules
![]() $P$
, all separated left
$P$
, all separated left
![]() $C$
-contramodules
$C$
-contramodules
![]() $Q$
, and all
$Q$
, and all
![]() $0\le i\le n$
. The map (33) is also injective for all left
$0\le i\le n$
. The map (33) is also injective for all left
![]() $C$
-contramodules
$C$
-contramodules
![]() $P$
and
$P$
and
![]() $Q$
and all
$Q$
and all
![]() $0\le i\le n-1$
.
$0\le i\le n-1$
.
8. Contramodule Ext isomorphism implies weakly finite Koszulity
The aim of this section is to prove the following theorem. Together with the results of the previous Sections 5–7, this will allow us to finish the proof of Theorem1.1 from the introduction.
Theorem 8.1.
Let
![]() $C$
be a conilpotent coalgebra over a field
$C$
be a conilpotent coalgebra over a field
![]() $k$
and
$k$
and
![]() $n\ge 1$
be the minimal integer for which the vector space
$n\ge 1$
be the minimal integer for which the vector space
![]() $\textrm {Ext}^n_C(k,k)$
is infinite-dimensional. Let
$\textrm {Ext}^n_C(k,k)$
is infinite-dimensional. Let
![]() $T$
be an infinite-dimensional
$T$
be an infinite-dimensional
![]() $k$
-vector space endowed with the trivial left
$k$
-vector space endowed with the trivial left
![]() $C$
-contramodule structure (provided by the coaugmentation
$C$
-contramodule structure (provided by the coaugmentation
![]() $\gamma :\ C\longrightarrow k$
). Then the map
$\gamma :\ C\longrightarrow k$
). Then the map
![]() $\textrm {Ext}^{C,n}(T,k)\longrightarrow \textrm {Ext}_{C^*}^n(T,k)$
induced by the contramodule forgetful functor
$\textrm {Ext}^{C,n}(T,k)\longrightarrow \textrm {Ext}_{C^*}^n(T,k)$
induced by the contramodule forgetful functor
![]() $\Theta :\ C{{-\mathsf{Contra}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
is not injective. Consequently, there exists a projective left
$\Theta :\ C{{-\mathsf{Contra}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
is not injective. Consequently, there exists a projective left
![]() $C$
-contramodule
$C$
-contramodule
![]() $P$
such that the map
$P$
such that the map
![]() $\textrm {Ext}^{C,n-1}(P,k)\longrightarrow \textrm {Ext}_{C^*}^{n-1}(P,k)$
induced by the functor
$\textrm {Ext}^{C,n-1}(P,k)\longrightarrow \textrm {Ext}_{C^*}^{n-1}(P,k)$
induced by the functor
![]() $\Theta$
is (injective, but) not surjective.
$\Theta$
is (injective, but) not surjective.
We start with a discussion of the case
![]() $n=1$
in Theorem8.1. This is the only case when
$n=1$
in Theorem8.1. This is the only case when
![]() $\textrm {Ext}^{C,n-1}(P,k)\ne 0$
.
$\textrm {Ext}^{C,n-1}(P,k)\ne 0$
.
Example 8.2.
Let
![]() $C$
be an infinitely cogenerated conilpotent coalgebra over
$C$
be an infinitely cogenerated conilpotent coalgebra over
![]() $k$
, and let
$k$
, and let
![]() $T$
be an infinite-dimensional vector space endowed with the trivial left
$T$
be an infinite-dimensional vector space endowed with the trivial left
![]() $C$
-contramodule structure. Then we claim that there exists a nonsplit short exact sequence of left
$C$
-contramodule structure. Then we claim that there exists a nonsplit short exact sequence of left
![]() $C$
-contramodules
$C$
-contramodules
that splits as a short exact sequence of left
![]() $C^*$
-modules. Consequently, the splitting map
$C^*$
-modules. Consequently, the splitting map
![]() $q:Q\longrightarrow k$
is a morphism of
$q:Q\longrightarrow k$
is a morphism of
![]() $C^*$
-modules but not a morphism of
$C^*$
-modules but not a morphism of
![]() $C$
-contramodules. So the forgetful functor
$C$
-contramodules. So the forgetful functor
![]() $\Theta$
is not full.
$\Theta$
is not full.
To construct the desired short exact sequence, put
![]() $C_+=C/\gamma (k)$
and
$C_+=C/\gamma (k)$
and
![]() $V=\ker (C_+\to C_+\otimes _k C_+)=\textrm {Ext}^1_C(k,k)$
, as in Example 6.4
. So we have
$V=\ker (C_+\to C_+\otimes _k C_+)=\textrm {Ext}^1_C(k,k)$
, as in Example 6.4
. So we have
![]() $F_0C=\gamma (k)$
and
$F_0C=\gamma (k)$
and
![]() $F_1C=F_0C\oplus V$
. Notice that
$F_1C=F_0C\oplus V$
. Notice that
![]() $V^*\otimes _kT$
is naturally a proper vector subspace in
$V^*\otimes _kT$
is naturally a proper vector subspace in
![]() $\textrm {Hom}_k(V,T)$
, as both the vector spaces
$\textrm {Hom}_k(V,T)$
, as both the vector spaces
![]() $V$
and
$V$
and
![]() $T$
are infinite-dimensional. Essentially,
$T$
are infinite-dimensional. Essentially,
![]() $V^*\otimes _kT\subset \textrm {Hom}_k(V,T)$
is the subspace of all linear maps
$V^*\otimes _kT\subset \textrm {Hom}_k(V,T)$
is the subspace of all linear maps
![]() $V\longrightarrow T$
of finite rank. Choose a linear function
$V\longrightarrow T$
of finite rank. Choose a linear function
![]() $\phi :\ \textrm {Hom}_k(V,T)\longrightarrow k$
vanishing on
$\phi :\ \textrm {Hom}_k(V,T)\longrightarrow k$
vanishing on
![]() $V^*\otimes _kT$
.
$V^*\otimes _kT$
.
Let the underlying vector space of
![]() $Q$
be simply the direct sum
$Q$
be simply the direct sum
![]() $k\oplus T$
. Define the contraaction map
$k\oplus T$
. Define the contraaction map
![]() $\pi :\ \textrm {Hom}_k(C,Q)\longrightarrow Q$
as follows. The component
$\pi :\ \textrm {Hom}_k(C,Q)\longrightarrow Q$
as follows. The component
![]() $\pi _{k,T}:\ \textrm {Hom}_k(C,k)\longrightarrow T$
of the map
$\pi _{k,T}:\ \textrm {Hom}_k(C,k)\longrightarrow T$
of the map
![]() $\pi$
is zero. The component
$\pi$
is zero. The component
![]() $\pi _{k,k}:\ \textrm {Hom}_k(C,k)\longrightarrow k$
is induced by the coaugmentation
$\pi _{k,k}:\ \textrm {Hom}_k(C,k)\longrightarrow k$
is induced by the coaugmentation
![]() $\gamma$
. The component
$\gamma$
. The component
![]() $\pi _{T,T}:\ \textrm {Hom}_k(C,T)\longrightarrow T$
is also induced by
$\pi _{T,T}:\ \textrm {Hom}_k(C,T)\longrightarrow T$
is also induced by
![]() $\gamma$
; specifically, it is defined as the composition
$\gamma$
; specifically, it is defined as the composition
![]() $\textrm {Hom}_k(C,T)\longrightarrow \textrm {Hom}_k(k,T)\longrightarrow T$
of the surjective map
$\textrm {Hom}_k(C,T)\longrightarrow \textrm {Hom}_k(k,T)\longrightarrow T$
of the surjective map
![]() $\textrm {Hom}_k(\gamma, T):\ \textrm {Hom}_k(C,T)\longrightarrow \textrm {Hom}_k(k,T)$
and the identity isomorphism
$\textrm {Hom}_k(\gamma, T):\ \textrm {Hom}_k(C,T)\longrightarrow \textrm {Hom}_k(k,T)$
and the identity isomorphism
![]() $\textrm {Hom}_k(k,T)\simeq T$
.
$\textrm {Hom}_k(k,T)\simeq T$
.
Finally, the component
![]() $\pi _{T,k}:\ \textrm {Hom}_k(C,T)\longrightarrow k$
of the map
$\pi _{T,k}:\ \textrm {Hom}_k(C,T)\longrightarrow k$
of the map
![]() $\pi$
is defined as the composition
$\pi$
is defined as the composition
![]() $\textrm {Hom}_k(C,T)\longrightarrow \textrm {Hom}_k(F_1C,T)\longrightarrow \textrm {Hom}_k(V,T)\longrightarrow k$
of the surjective map
$\textrm {Hom}_k(C,T)\longrightarrow \textrm {Hom}_k(F_1C,T)\longrightarrow \textrm {Hom}_k(V,T)\longrightarrow k$
of the surjective map
![]() $\textrm {Hom}_k(C,T)\longrightarrow \textrm {Hom}_k(F_1C,T)$
induced by the inclusion
$\textrm {Hom}_k(C,T)\longrightarrow \textrm {Hom}_k(F_1C,T)$
induced by the inclusion
![]() $F_1C\longrightarrow C$
, the direct summand projection
$F_1C\longrightarrow C$
, the direct summand projection
![]() $\textrm {Hom}_k(F_1C,T)=\textrm {Hom}_k(F_0C\oplus V,\ T)\longrightarrow \textrm {Hom}_k(V,T)$
, and the chosen linear function
$\textrm {Hom}_k(F_1C,T)=\textrm {Hom}_k(F_0C\oplus V,\ T)\longrightarrow \textrm {Hom}_k(V,T)$
, and the chosen linear function
![]() $\phi :\ \textrm {Hom}_k(V,T)\longrightarrow k$
.
$\phi :\ \textrm {Hom}_k(V,T)\longrightarrow k$
.
Then the direct sum decomposition of vector spaces
![]() $Q=k\oplus T$
still holds as a direct sum decomposition in the module category
$Q=k\oplus T$
still holds as a direct sum decomposition in the module category
![]() $C^*{{-\mathsf{Mod}}}$
, since the composition of the embedding
$C^*{{-\mathsf{Mod}}}$
, since the composition of the embedding
![]() $C^*\otimes _k T \longrightarrow \textrm {Hom}_k(C,T)$
with the map
$C^*\otimes _k T \longrightarrow \textrm {Hom}_k(C,T)$
with the map
![]() $\pi _{T,k}:\ \textrm {Hom}_k(C,T)\longrightarrow k$
is the zero map. But the
$\pi _{T,k}:\ \textrm {Hom}_k(C,T)\longrightarrow k$
is the zero map. But the
![]() $C$
-contramodule structure on
$C$
-contramodule structure on
![]() $Q$
is nontrivial (not induced by the coaugmentation
$Q$
is nontrivial (not induced by the coaugmentation
![]() $\gamma$
), so
$\gamma$
), so
![]() $Q$
is not isomorphic to
$Q$
is not isomorphic to
![]() $k\oplus T$
in
$k\oplus T$
in
![]() $C{{-\mathsf{Contra}}}$
.
$C{{-\mathsf{Contra}}}$
.
In order to pass from some object
![]() $Q$
in Example 8.2 to a projective object
$Q$
in Example 8.2 to a projective object
![]() $P$
in the context Theorem8.1 for
$P$
in the context Theorem8.1 for
![]() $n=1$
, we will use Lemma A.7 from the appendix.
$n=1$
, we will use Lemma A.7 from the appendix.
In the case
![]() $n\gt 1$
, we need the following simple coalgebra-theoretic lemma.
$n\gt 1$
, we need the following simple coalgebra-theoretic lemma.
Lemma 8.3.
Let
![]() $(C,\gamma )$
be a coaugmented coalgebra,
$(C,\gamma )$
be a coaugmented coalgebra,
![]() $N$
be a right
$N$
be a right
![]() $C$
-comodule, and
$C$
-comodule, and
![]() $T$
be a
$T$
be a
![]() $k$
-vector space. Then there is a natural isomorphism of
$k$
-vector space. Then there is a natural isomorphism of
![]() $k$
-vector spaces
$k$
-vector spaces
Proof.
One has
![]() ${}^\gamma \!\textrm {Hom}_k(N,T)\simeq \textrm {Hom}_k(N_\gamma, T)$
by formula (4) from Section 3. Hence
${}^\gamma \!\textrm {Hom}_k(N,T)\simeq \textrm {Hom}_k(N_\gamma, T)$
by formula (4) from Section 3. Hence
as desired (cf. Lemma 6.5).
Proposition 8.4.
Let
![]() $C$
be a finitely cogenerated conilpotent coalgebra over a field
$C$
be a finitely cogenerated conilpotent coalgebra over a field
![]() $k$
and
$k$
and
![]() $n\ge 2$
be the minimal integer for which the vector space
$n\ge 2$
be the minimal integer for which the vector space
![]() $\textrm {Ext}^n_C(k,k)$
is infinite-dimensional. Let
$\textrm {Ext}^n_C(k,k)$
is infinite-dimensional. Let
![]() $T$
be an infinite-dimensional
$T$
be an infinite-dimensional
![]() $k$
-vector space endowed with the trivial left
$k$
-vector space endowed with the trivial left
![]() $C$
-contramodule structure (provided by the coaugmentation
$C$
-contramodule structure (provided by the coaugmentation
![]() $\gamma$
). Then the map
$\gamma$
). Then the map
![]() $\textrm {Ext}^{C,n}(T,k)\longrightarrow \textrm {Ext}_{C^*}^n(T,k)$
induced by the contramodule forgetful functor
$\textrm {Ext}^{C,n}(T,k)\longrightarrow \textrm {Ext}_{C^*}^n(T,k)$
induced by the contramodule forgetful functor
![]() $\Theta :\ C{{-\mathsf{Contra}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
is surjective, but not injective. Consequently, one has
$\Theta :\ C{{-\mathsf{Contra}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
is surjective, but not injective. Consequently, one has
![]() $\textrm {Ext}_{C^*}^{n-1}(P,k)\ne 0$
for the projective/free left
$\textrm {Ext}_{C^*}^{n-1}(P,k)\ne 0$
for the projective/free left
![]() $C$
-contramodule
$C$
-contramodule
![]() $P=\textrm {Hom}_k(C,T)$
.
$P=\textrm {Hom}_k(C,T)$
.
Proof.
Our strategy of proving the first assertion of the proposition is to explicitly compute the map of Ext spaces in question, and see that it is surjective but not injective. As in the proof of Theorem5.1, we choose a minimal injective/cofree coresolution (14) of the right
![]() $C$
-comodule
$C$
-comodule
![]() $k$
,
$k$
,
The vector space
![]() $V_i\simeq \textrm {Ext}^i_{C^{\mathrm{op}}}(k,k)\simeq \textrm {Ext}^i_C(k,k)$
is finite-dimensional for
$V_i\simeq \textrm {Ext}^i_{C^{\mathrm{op}}}(k,k)\simeq \textrm {Ext}^i_C(k,k)$
is finite-dimensional for
![]() $0\le i\le n-1$
and infinite-dimensional for
$0\le i\le n-1$
and infinite-dimensional for
![]() $i=n$
by assumption.
$i=n$
by assumption.
Applying the contravariant vector space Hom functor
![]() $\textrm {Hom}_k({-},T)$
to the complex (34), we obtain a minimal projective resolution of the left
$\textrm {Hom}_k({-},T)$
to the complex (34), we obtain a minimal projective resolution of the left
![]() $C$
-contramodule
$C$
-contramodule
![]() $T$
,
$T$
,
 \begin{align} 0\longleftarrow T\longleftarrow \textrm {Hom}_k(C,\textrm {Hom}_k(V_0,T))\longleftarrow \textrm {Hom}_k(C,\textrm {Hom}_k(V_1,T))\longleftarrow \dotsb \\ \nonumber \longleftarrow \textrm {Hom}_k(C,\textrm {Hom}_k(V_{n-1},T)) \longleftarrow \textrm {Hom}_k(C,\textrm {Hom}_k(V_n,T)) \\ \nonumber \longleftarrow \textrm {Hom}_k(C,\textrm {Hom}_k(V_{n+1},T))\longleftarrow \dotsb \end{align}
\begin{align} 0\longleftarrow T\longleftarrow \textrm {Hom}_k(C,\textrm {Hom}_k(V_0,T))\longleftarrow \textrm {Hom}_k(C,\textrm {Hom}_k(V_1,T))\longleftarrow \dotsb \\ \nonumber \longleftarrow \textrm {Hom}_k(C,\textrm {Hom}_k(V_{n-1},T)) \longleftarrow \textrm {Hom}_k(C,\textrm {Hom}_k(V_n,T)) \\ \nonumber \longleftarrow \textrm {Hom}_k(C,\textrm {Hom}_k(V_{n+1},T))\longleftarrow \dotsb \end{align}
On the other hand, applying the dual vector space functor
![]() $\textrm {Hom}_k({-},k)$
to the complex (34), we obtain a resolution of the left
$\textrm {Hom}_k({-},k)$
to the complex (34), we obtain a resolution of the left
![]() $C^*$
-module
$C^*$
-module
![]() $k$
$k$
as in formula (24) from the proof of Proposition 6.6. Applying the vector space tensor product functor
![]() ${-}\otimes _k T$
to the complex (36), we get an initially projective resolution of the left
${-}\otimes _k T$
to the complex (36), we get an initially projective resolution of the left
![]() $C^*$
-module
$C^*$
-module
![]() $T$
,
$T$
,
For any left
![]() $C$
-contramodule
$C$
-contramodule
![]() $Y$
, the projective resolution (35) of the trivial left
$Y$
, the projective resolution (35) of the trivial left
![]() $C$
-contramodule
$C$
-contramodule
![]() $T$
can be used in order to compute the vector spaces
$T$
can be used in order to compute the vector spaces
![]() $\textrm {Ext}^{C,i}(T,Y)$
in all cohomological degrees
$\textrm {Ext}^{C,i}(T,Y)$
in all cohomological degrees
![]() $i\ge 0$
. On the other hand, the resolution (37) of the trivial left
$i\ge 0$
. On the other hand, the resolution (37) of the trivial left
![]() $C^*$
-module
$C^*$
-module
![]() $T$
is only initially projective. By Lemma A.1, for any left
$T$
is only initially projective. By Lemma A.1, for any left
![]() $C^*$
-module
$C^*$
-module
![]() $Y$
, the resolution (37) can be used in order to compute the vector spaces
$Y$
, the resolution (37) can be used in order to compute the vector spaces
![]() $\textrm {Ext}_{C^*}^i(T,Y)$
in the cohomological degrees
$\textrm {Ext}_{C^*}^i(T,Y)$
in the cohomological degrees
![]() $0\le i\le n$
.
$0\le i\le n$
.
Now we have a natural injective morphism of complexes of left
![]() $C^*$
-modules from the complex (37) to the complex (35), acting by the identity map on the leftmost terms
$C^*$
-modules from the complex (37) to the complex (35), acting by the identity map on the leftmost terms
![]() $T$
. This morphism of resolutions can be used in order to compute the maps
$T$
. This morphism of resolutions can be used in order to compute the maps
![]() $\textrm {Ext}^{C,i}(T,Y) \longrightarrow \textrm {Ext}_{C^*}^i(T,Y)$
in the cohomological degrees
$\textrm {Ext}^{C,i}(T,Y) \longrightarrow \textrm {Ext}_{C^*}^i(T,Y)$
in the cohomological degrees
![]() $0\le i\le n$
for any left
$0\le i\le n$
for any left
![]() $C$
-contramodule
$C$
-contramodule
![]() $Y$
.
$Y$
.
Put
![]() $Y=k$
. Applying the contramodule Hom functor
$Y=k$
. Applying the contramodule Hom functor
![]() $\textrm {Hom}^C({-},k)$
to the projective resolution (35) of the trivial left
$\textrm {Hom}^C({-},k)$
to the projective resolution (35) of the trivial left
![]() $C$
-contramodule
$C$
-contramodule
![]() $T$
, we obtain a complex
$T$
, we obtain a complex
By Lemma 8.3, the complex (38) is naturally isomorphic to the complex obtained by applying the functor
![]() $\textrm {Hom}_k(({-})_\gamma, T)^*$
to the coresolution (34). As the latter coresolution was chosen to be minimal, the differential in the complex (38) vanishes.
$\textrm {Hom}_k(({-})_\gamma, T)^*$
to the coresolution (34). As the latter coresolution was chosen to be minimal, the differential in the complex (38) vanishes.
Applying the module Hom functor
![]() $\textrm {Hom}_{C^*}({-},k)$
to the initially projective resolution (37) of the trivial left
$\textrm {Hom}_{C^*}({-},k)$
to the initially projective resolution (37) of the trivial left
![]() $C^*$
-module
$C^*$
-module
![]() $T$
, we obtain a complex
$T$
, we obtain a complex
The complex (39) can be also obtained by applying the covariant vector space Hom functor
![]() $\textrm {Hom}_k(T,{-})$
to the complex
$\textrm {Hom}_k(T,{-})$
to the complex
produced by applying the module Hom functor
![]() $\textrm {Hom}_{C^*}({-},k)$
to the resolution (36) of the trivial
$\textrm {Hom}_{C^*}({-},k)$
to the resolution (36) of the trivial
![]() $C^*$
-module
$C^*$
-module
![]() $k$
(see formula (25) in the proof of Proposition 6.6).
$k$
(see formula (25) in the proof of Proposition 6.6).
By Lemma 6.5, the complex (40) is naturally isomorphic to the complex
obtained by applying the functor
![]() $(({-})_\gamma )^{**}$
to the coresolution (34). Once again, as the latter coresolution was chosen to be minimal, the differential in the complex (41) (or, which is the same, in the complex (40)) vanishes. We have computed the complex (39) as having the form
$(({-})_\gamma )^{**}$
to the coresolution (34). Once again, as the latter coresolution was chosen to be minimal, the differential in the complex (41) (or, which is the same, in the complex (40)) vanishes. We have computed the complex (39) as having the form
or, which is the same,
and zero differential.
Now it is finally clear from the formulas (38) and (43) that the map
is isomorphic to the natural map
which can be obtained by applying the dual vector space functor
![]() $\textrm {Hom}_k({-},k)$
to the natural embedding
$\textrm {Hom}_k({-},k)$
to the natural embedding
The map (46) is always injective, but for infinite-dimensional vector spaces
![]() $V_n$
and
$V_n$
and
![]() $T$
it is not surjective. Thus, the map (45), and consequently the desired map (44), is surjective but not injective.
$T$
it is not surjective. Thus, the map (45), and consequently the desired map (44), is surjective but not injective.
To deduce the second assertion of the proposition, we apply Lemma A.4(b) to the contramodule forgetful functor
![]() $\Phi =\Theta$
, the left
$\Phi =\Theta$
, the left
![]() $C$
-contramodule
$C$
-contramodule
![]() $Y=k$
, and the natural epimorphism of left
$Y=k$
, and the natural epimorphism of left
![]() $C$
-contramodules
$C$
-contramodules
![]() $P=\textrm {Hom}_k(C,T) \longrightarrow T$
with a kernel
$P=\textrm {Hom}_k(C,T) \longrightarrow T$
with a kernel
![]() $X$
. By the first assertion of the proposition, there exists a nonzero extension class
$X$
. By the first assertion of the proposition, there exists a nonzero extension class
![]() $\beta \in \textrm {Ext}^{C,n}(T,Y)$
annihilated by the map (44). The class
$\beta \in \textrm {Ext}^{C,n}(T,Y)$
annihilated by the map (44). The class
![]() $\beta$
is also annihilated by the map
$\beta$
is also annihilated by the map
![]() $\textrm {Ext}^{C,n}(T,Y)\longrightarrow \textrm {Ext}^{C,n}(P,Y)=0$
(as
$\textrm {Ext}^{C,n}(T,Y)\longrightarrow \textrm {Ext}^{C,n}(P,Y)=0$
(as
![]() $n\ge 2$
and the
$n\ge 2$
and the
![]() $C$
-contramodule
$C$
-contramodule
![]() $P$
is projective). Finally, the map
$P$
is projective). Finally, the map
![]() $\textrm {Ext}^{C,n-1}(X,Y)\longrightarrow \textrm {Ext}_{C^*}^{n-1}(X,Y)$
is injective by Corollary 7.5 (since the left
$\textrm {Ext}^{C,n-1}(X,Y)\longrightarrow \textrm {Ext}_{C^*}^{n-1}(X,Y)$
is injective by Corollary 7.5 (since the left
![]() $C$
-contramodule
$C$
-contramodule
![]() $Y=k$
is separated). So Lemma A.4(b) tells us that the map
$Y=k$
is separated). So Lemma A.4(b) tells us that the map
![]() $0=\textrm {Ext}^{C,n-1}(P,Y)\longrightarrow \textrm {Ext}_{C^*}^{n-1}(P,Y)$
cannot be surjective.
$0=\textrm {Ext}^{C,n-1}(P,Y)\longrightarrow \textrm {Ext}_{C^*}^{n-1}(P,Y)$
cannot be surjective.
Proof of Theorem
8.1. The case
![]() $n=1$
is covered by Example 8.2 with Lemma A.7. The case
$n=1$
is covered by Example 8.2 with Lemma A.7. The case
![]() $n\ge 2$
is treated in Proposition 8.4.
$n\ge 2$
is treated in Proposition 8.4.
Proof of Theorem
1.1. Follows from Theorems5.1, 6.1, 7.2, 8.1 (applied to the coalgebras
![]() $C$
and
$C$
and
![]() $C^{\mathrm{op}}$
) and Propositions 4.1, 4.3. Specifically:
$C^{\mathrm{op}}$
) and Propositions 4.1, 4.3. Specifically:
(iv)
![]() $\Longrightarrow$
(i) is Theorem5.1;
$\Longrightarrow$
(i) is Theorem5.1;
(i)
![]() $\Longrightarrow$
(iv) is the first assertion of Theorem6.1;
$\Longrightarrow$
(iv) is the first assertion of Theorem6.1;
(iv)
![]() $\Longrightarrow$
(ii) is Theorem5.1 for the coalgebra
$\Longrightarrow$
(ii) is Theorem5.1 for the coalgebra
![]() $C^{\mathrm{op}}$
together with Proposition 4.1;
$C^{\mathrm{op}}$
together with Proposition 4.1;
(ii)
![]() $\Longrightarrow$
(iv) is the first assertion of Theorem6.1 for the coalgebra
$\Longrightarrow$
(iv) is the first assertion of Theorem6.1 for the coalgebra
![]() $C^{\mathrm{op}}$
together with Proposition 4.1;
$C^{\mathrm{op}}$
together with Proposition 4.1;
(iv)
![]() $\Longrightarrow$
(iii) is the first assertion of Theorem7.2;
$\Longrightarrow$
(iii) is the first assertion of Theorem7.2;
(iii)
![]() $\Longrightarrow$
(iv) is the second assertion of Theorem8.1;
$\Longrightarrow$
(iv) is the second assertion of Theorem8.1;
(iv)
![]() $\Longleftrightarrow$
(v) is Proposition 4.3.
$\Longleftrightarrow$
(v) is Proposition 4.3.
The last assertion of Theorem1.1 is provided by the second assertion of Theorem7.2.
9. Half-bounded derived full-and-faithfulness
The aim of this short section is to finish the proof of Theorem1.2 from the introduction. The argument is based on the following result from the preprint [Reference Positselski31].
Proposition 9.1. (a) Let
![]() $\mathsf{A}$
and
$\mathsf{A}$
and
![]() $\mathsf{B}$
be abelian categories, and
$\mathsf{B}$
be abelian categories, and
![]() $\Upsilon :\ \mathsf{B}\longrightarrow \mathsf{A}$
be a fully faithful exact functor. Assume that there are enough injective objects in the abelian category
$\Upsilon :\ \mathsf{B}\longrightarrow \mathsf{A}$
be a fully faithful exact functor. Assume that there are enough injective objects in the abelian category
![]() $\mathsf{A}$
, and the functor
$\mathsf{A}$
, and the functor
![]() $\Upsilon$
has a right adjoint functor
$\Upsilon$
has a right adjoint functor
![]() $\Gamma :\ \mathsf{A}\longrightarrow \mathsf{B}$
. Then the induced triangulated functor between the bounded derived categories
$\Gamma :\ \mathsf{A}\longrightarrow \mathsf{B}$
. Then the induced triangulated functor between the bounded derived categories
![]() $\Upsilon ^{\mathsf{b}}:\ \mathsf{D}^{\mathsf{b}}(\mathsf{B})\longrightarrow \mathsf{D}^{\mathsf{b}}(\mathsf{A})$
is fully faithful if and only if the induced triangulated functor between the bounded below derived categories
$\Upsilon ^{\mathsf{b}}:\ \mathsf{D}^{\mathsf{b}}(\mathsf{B})\longrightarrow \mathsf{D}^{\mathsf{b}}(\mathsf{A})$
is fully faithful if and only if the induced triangulated functor between the bounded below derived categories
![]() $\Upsilon ^+:\ \mathsf{D}^+(\mathsf{B})\longrightarrow \mathsf{D}^+(\mathsf{A})$
is fully faithful.
$\Upsilon ^+:\ \mathsf{D}^+(\mathsf{B})\longrightarrow \mathsf{D}^+(\mathsf{A})$
is fully faithful.
(b) Let
![]() $\mathsf{A}$
and
$\mathsf{A}$
and
![]() $\mathsf{B}$
be abelian categories, and
$\mathsf{B}$
be abelian categories, and
![]() $\Theta :\ \mathsf{B}\longrightarrow \mathsf{A}$
be a fully faithful exact functor. Assume that there are enough projective objects in the abelian category
$\Theta :\ \mathsf{B}\longrightarrow \mathsf{A}$
be a fully faithful exact functor. Assume that there are enough projective objects in the abelian category
![]() $\mathsf{A}$
, and the functor
$\mathsf{A}$
, and the functor
![]() $\Theta$
has a left adjoint functor
$\Theta$
has a left adjoint functor
![]() $\Delta :\ \mathsf{A}\longrightarrow \mathsf{B}$
. Then the induced triangulated functor between the bounded derived categories
$\Delta :\ \mathsf{A}\longrightarrow \mathsf{B}$
. Then the induced triangulated functor between the bounded derived categories
![]() $\Theta ^{\mathsf{b}}:\ \mathsf{D}^{\mathsf{b}}(\mathsf{B})\longrightarrow \mathsf{D}^{\mathsf{b}}(\mathsf{A})$
is fully faithful if and only if the induced triangulated functor between the bounded above derived categories
$\Theta ^{\mathsf{b}}:\ \mathsf{D}^{\mathsf{b}}(\mathsf{B})\longrightarrow \mathsf{D}^{\mathsf{b}}(\mathsf{A})$
is fully faithful if and only if the induced triangulated functor between the bounded above derived categories
![]() $\Theta ^-:\ \mathsf{D}^-(\mathsf{B})\longrightarrow \mathsf{D}^-(\mathsf{A})$
is fully faithful.
$\Theta ^-:\ \mathsf{D}^-(\mathsf{B})\longrightarrow \mathsf{D}^-(\mathsf{A})$
is fully faithful.
Proof.
Part (b) is [Reference Positselski31, Proposition 6.5 (c)
![]() $\Leftrightarrow$
(d)]. The point is that any one of the functors
$\Leftrightarrow$
(d)]. The point is that any one of the functors
![]() $\Theta ^{\mathsf{b}}$
and
$\Theta ^{\mathsf{b}}$
and
![]() $\Theta ^-$
is fully faithful if and only if the higher left derived functors
$\Theta ^-$
is fully faithful if and only if the higher left derived functors
![]() $\mathbb L_n\Delta :\ \mathsf{A}\longrightarrow \mathsf{B}$
,
$\mathbb L_n\Delta :\ \mathsf{A}\longrightarrow \mathsf{B}$
,
![]() $n\ge 1$
of the functor
$n\ge 1$
of the functor
![]() $\Delta$
vanish on the essential image of the functor
$\Delta$
vanish on the essential image of the functor
![]() $\Theta$
. Part (a) is the dual assertion.
$\Theta$
. Part (a) is the dual assertion.
Proof of Theorem 1.2. Follows from Theorem1.1 and Proposition 9.1. Specifically:
(i)
![]() $\Longleftrightarrow$
(vii) is Theorem1.1(i)
$\Longleftrightarrow$
(vii) is Theorem1.1(i)
![]() $\Leftrightarrow$
(iv);
$\Leftrightarrow$
(iv);
(iii)
![]() $\Longleftrightarrow$
(vii) is Theorem1.1(ii)
$\Longleftrightarrow$
(vii) is Theorem1.1(ii)
![]() $\Leftrightarrow$
(iv);
$\Leftrightarrow$
(iv);
(v)
![]() $\Longleftrightarrow$
(vii) is Theorem1.1(iii)
$\Longleftrightarrow$
(vii) is Theorem1.1(iii)
![]() $\Leftrightarrow$
(iv) and the last assertion of Theorem1.1;
$\Leftrightarrow$
(iv) and the last assertion of Theorem1.1;
(vii)
![]() $\Longleftrightarrow$
(viii) is Theorem1.1(iv)
$\Longleftrightarrow$
(viii) is Theorem1.1(iv)
![]() $\Leftrightarrow$
(v);
$\Leftrightarrow$
(v);
(i)
![]() $\Longleftrightarrow$
(ii) is Proposition 9.1(a);
$\Longleftrightarrow$
(ii) is Proposition 9.1(a);
(iii)
![]() $\Longleftrightarrow$
(iv) is Proposition 9.1(a);
$\Longleftrightarrow$
(iv) is Proposition 9.1(a);
(v)
![]() $\Longleftrightarrow$
(vi) is Proposition 9.1(b).
$\Longleftrightarrow$
(vi) is Proposition 9.1(b).
In order to apply Proposition 9.1, it only needs to be explained why the functor
![]() $\Upsilon :\ C{{-\mathsf{Comod}}} \longrightarrow C^*{{-\mathsf{Mod}}}$
has a right adjoint and why the functor
$\Upsilon :\ C{{-\mathsf{Comod}}} \longrightarrow C^*{{-\mathsf{Mod}}}$
has a right adjoint and why the functor
![]() $\Theta :\ C{{-\mathsf{Contra}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
has a left adjoint. In fact, these are quite general properties of coalgebras, as the assumption that
$\Theta :\ C{{-\mathsf{Contra}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
has a left adjoint. In fact, these are quite general properties of coalgebras, as the assumption that
![]() $C$
is conilpotent is not needed here.
$C$
is conilpotent is not needed here.
For any coalgebra
![]() $C$
over a field
$C$
over a field
![]() $k$
, the comodule inclusion functor
$k$
, the comodule inclusion functor
![]() $\Upsilon :\ C{{-\mathsf{Comod}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
has a right adjoint functor
$\Upsilon :\ C{{-\mathsf{Comod}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
has a right adjoint functor
![]() $\Gamma :\ C^*{{-\mathsf{Mod}}}\longrightarrow C{{-\mathsf{Comod}}}$
. The functor
$\Gamma :\ C^*{{-\mathsf{Mod}}}\longrightarrow C{{-\mathsf{Comod}}}$
. The functor
![]() $\Gamma$
assigns to every left
$\Gamma$
assigns to every left
![]() $C^*$
-module
$C^*$
-module
![]() $N$
its maximal submodule belonging to the essential image of the functor
$N$
its maximal submodule belonging to the essential image of the functor
![]() $\Upsilon$
. In other words,
$\Upsilon$
. In other words,
![]() $\Gamma (N)$
is the sum of all submodules of
$\Gamma (N)$
is the sum of all submodules of
![]() $N$
whose
$N$
whose
![]() $C^*$
-module structure comes from a
$C^*$
-module structure comes from a
![]() $C$
-comodule structure. Equivalently,
$C$
-comodule structure. Equivalently,
![]() $\Gamma (N)\subset N$
is the submodule consisting of all the elements
$\Gamma (N)\subset N$
is the submodule consisting of all the elements
![]() $x\in N$
whose annihilator ideals in
$x\in N$
whose annihilator ideals in
![]() $C^*$
(with respect to the action map
$C^*$
(with respect to the action map
![]() $C^*\times N\longrightarrow N$
) contain the annihilator of some finite-dimensional vector subspace of
$C^*\times N\longrightarrow N$
) contain the annihilator of some finite-dimensional vector subspace of
![]() $C$
(with respect to the pairing map
$C$
(with respect to the pairing map
![]() $C^*\times C\longrightarrow k$
) [Reference Sweedler44, Theorem 2.1.3(d)].
$C^*\times C\longrightarrow k$
) [Reference Sweedler44, Theorem 2.1.3(d)].
For any coalgebra
![]() $C$
over a field
$C$
over a field
![]() $k$
, the contramodule forgetful functor
$k$
, the contramodule forgetful functor
![]() $\Theta :\ C{{-\mathsf{Contra}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
has a left adjoint functor
$\Theta :\ C{{-\mathsf{Contra}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
has a left adjoint functor
![]() $\Delta :\ C^*{{-\mathsf{Mod}}}\longrightarrow C{{-\mathsf{Contra}}}$
. Given a left
$\Delta :\ C^*{{-\mathsf{Mod}}}\longrightarrow C{{-\mathsf{Contra}}}$
. Given a left
![]() $C^*$
-module
$C^*$
-module
![]() $M$
, the adjunction morphism
$M$
, the adjunction morphism
![]() $M\longrightarrow \Delta (M)$
is not surjective in general; so
$M\longrightarrow \Delta (M)$
is not surjective in general; so
![]() $\Delta (M)$
cannot be constructed as a quotient (contra)module of
$\Delta (M)$
cannot be constructed as a quotient (contra)module of
![]() $M$
.
$M$
.
To construct the functor
![]() $\Delta$
, one defines it on free
$\Delta$
, one defines it on free
![]() $C^*$
-modules by the rule
$C^*$
-modules by the rule
![]() $\Delta (C^*\otimes _k V)=\textrm {Hom}_k(C,V)$
for every
$\Delta (C^*\otimes _k V)=\textrm {Hom}_k(C,V)$
for every
![]() $k$
-vector space
$k$
-vector space
![]() $V$
. Functoriality of the category object corepresenting a (given corepresentable) functor provides a natural way to define the action of
$V$
. Functoriality of the category object corepresenting a (given corepresentable) functor provides a natural way to define the action of
![]() $\Delta$
on morphisms of free
$\Delta$
on morphisms of free
![]() $C^*$
-modules. Then there is always a unique way to extend an abelian category-valued covariant additive functor defined on the full subcategory of free modules over some ring
$C^*$
-modules. Then there is always a unique way to extend an abelian category-valued covariant additive functor defined on the full subcategory of free modules over some ring
![]() $R$
to a right exact functor on the category of all
$R$
to a right exact functor on the category of all
![]() $R$
-modules. Simply put, to compute the contramodule
$R$
-modules. Simply put, to compute the contramodule
![]() $\Delta (M)$
, one needs to represent
$\Delta (M)$
, one needs to represent
![]() $M$
as the cokernel of a morphism of free
$M$
as the cokernel of a morphism of free
![]() $C^*$
-modules
$C^*$
-modules
![]() $f:\ F'\longrightarrow F''$
; then,
$f:\ F'\longrightarrow F''$
; then,
![]() $\Delta (M)$
is the cokernel of the contramodule map
$\Delta (M)$
is the cokernel of the contramodule map
![]() $\Delta (f):\Delta (F')\longrightarrow \Delta (F'')$
.
$\Delta (f):\Delta (F')\longrightarrow \Delta (F'')$
.
Remark 9.2. Following the philosophy of the book [Reference Positselski20 ] and the memoir [Reference Positselski21 ] (see also the discussion in the survey [Reference Positselski36, Section 7]), one is generally supposed to consider the coderived category of
![]() $C$
-comodules
$C$
-comodules
![]() $\mathsf{D}^{\mathsf{co}}(C{{-\mathsf{Comod}}})$
and the contraderived category of
$\mathsf{D}^{\mathsf{co}}(C{{-\mathsf{Comod}}})$
and the contraderived category of
![]() $C$
-contramodules
$C$
-contramodules
![]() $\mathsf{D}^{\mathsf{ctr}}(C{{-\mathsf{Contra}}})$
, rather than the conventional derived categories
$\mathsf{D}^{\mathsf{ctr}}(C{{-\mathsf{Contra}}})$
, rather than the conventional derived categories
![]() $\mathsf{D}(C{{-\mathsf{Comod}}})$
and
$\mathsf{D}(C{{-\mathsf{Comod}}})$
and
![]() $\mathsf{D}(C{{-\mathsf{Contra}}})$
. Let us point out, in this connection, that the difference between the derived and the co/contraderived categories mostly does not manifest itself in the context of the present paper; certainly not in the context of Theorem 1.2. The point is that the distinction between the conventional derived and the co/contraderived categories of abelian categories is only relevant for unbounded complexes, while the results of the present paper mostly concern the
$\mathsf{D}(C{{-\mathsf{Contra}}})$
. Let us point out, in this connection, that the difference between the derived and the co/contraderived categories mostly does not manifest itself in the context of the present paper; certainly not in the context of Theorem 1.2. The point is that the distinction between the conventional derived and the co/contraderived categories of abelian categories is only relevant for unbounded complexes, while the results of the present paper mostly concern the
![]() $\textrm {Ext}$
spaces, which can be computed in the bounded derived categories.
$\textrm {Ext}$
spaces, which can be computed in the bounded derived categories.
Specifically, let
![]() $\mathsf{A}$
be an abelian category with exact functors of infinite coproduct. Then the natural triangulated functor from the coderived to the derived category
$\mathsf{A}$
be an abelian category with exact functors of infinite coproduct. Then the natural triangulated functor from the coderived to the derived category
![]() $\mathsf{D}^{\mathsf{co}}(\mathsf{A})\longrightarrow \mathsf{D}(\mathsf{A})$
induces an equivalence of the full subcategories of bounded below complexes,
$\mathsf{D}^{\mathsf{co}}(\mathsf{A})\longrightarrow \mathsf{D}(\mathsf{A})$
induces an equivalence of the full subcategories of bounded below complexes,
![]() $\mathsf{D}^{{\mathsf{co}},+}(\mathsf{A}) \simeq \mathsf{D}^+(\mathsf{A})$
. Dually, if
$\mathsf{D}^{{\mathsf{co}},+}(\mathsf{A}) \simeq \mathsf{D}^+(\mathsf{A})$
. Dually, if
![]() $\mathsf{B}$
is an abelian category with exact functors of infinite product, then the natural triangulated functor from the contraderived to the derived category
$\mathsf{B}$
is an abelian category with exact functors of infinite product, then the natural triangulated functor from the contraderived to the derived category
![]() $\mathsf{D}^{\mathsf{ctr}}(\mathsf{B})\longrightarrow \mathsf{D}(\mathsf{B})$
induces an equivalence of the full subcategories of bounded above complexes,
$\mathsf{D}^{\mathsf{ctr}}(\mathsf{B})\longrightarrow \mathsf{D}(\mathsf{B})$
induces an equivalence of the full subcategories of bounded above complexes,
![]() $\mathsf{D}^{{\mathsf{ctr}},-}(\mathsf{B})\simeq \mathsf{D}^-(\mathsf{B})$
[Reference Positselski21, Theorems 3.4.1 and 4.3.1], [Reference Positselski23, Lemma A.1.3]. These references cover the case of co/contraderived categories in the sense of Positselski (see [Reference Positselski36, Section 7] for the terminology); for a similar result for coderived categories in the sense of Becker, assume that there are enough injective objects in
$\mathsf{D}^{{\mathsf{ctr}},-}(\mathsf{B})\simeq \mathsf{D}^-(\mathsf{B})$
[Reference Positselski21, Theorems 3.4.1 and 4.3.1], [Reference Positselski23, Lemma A.1.3]. These references cover the case of co/contraderived categories in the sense of Positselski (see [Reference Positselski36, Section 7] for the terminology); for a similar result for coderived categories in the sense of Becker, assume that there are enough injective objects in
![]() $\mathsf{A}$
, denote the full subcategory of injective objects by
$\mathsf{A}$
, denote the full subcategory of injective objects by
![]() $\mathsf{E}=\mathsf{A}_{\mathsf{inj}}\subset \mathsf{A}$
, and refer to [Reference Positselski and Št’ovíček38, Lemma 5.4]. See also [Reference Positselski20, Remark 4.1].
$\mathsf{E}=\mathsf{A}_{\mathsf{inj}}\subset \mathsf{A}$
, and refer to [Reference Positselski and Št’ovíček38, Lemma 5.4]. See also [Reference Positselski20, Remark 4.1].
10. Co-Noetherian and cocoherent conilpotent coalgebras
The aim of this section is to explain that certain Noetherianity or coherence-type conditions on a conilpotent coalgebra
![]() $C$
imply weakly finite Koszulity. In particular, all cocommutative conilpotent coalgebras are weakly finitely Koszul; this fact will be relevant for the discussion in the next Section 11.
$C$
imply weakly finite Koszulity. In particular, all cocommutative conilpotent coalgebras are weakly finitely Koszul; this fact will be relevant for the discussion in the next Section 11.
Let
![]() $C$
be a coalgebra over a field
$C$
be a coalgebra over a field
![]() $k$
. A left
$k$
. A left
![]() $C$
-comodule is said to be finitely cogenerated if it can be embedded as a subcomodule into a cofree
$C$
-comodule is said to be finitely cogenerated if it can be embedded as a subcomodule into a cofree
![]() $C$
-comodule
$C$
-comodule
![]() $C\otimes _k V$
with a finite-dimensional space of cogenerators
$C\otimes _k V$
with a finite-dimensional space of cogenerators
![]() $V$
. A coalgebra
$V$
. A coalgebra
![]() $C$
is said to be left co-Noetherian if every quotient comodule of a finitely cogenerated left
$C$
is said to be left co-Noetherian if every quotient comodule of a finitely cogenerated left
![]() $C$
-comodule is finitely cogenerated [Reference Gómez-Torrecillas, Năstăsescu and Torrecillas9, Reference Positselski29, Reference Wang and Wu47]. A coalgebra
$C$
-comodule is finitely cogenerated [Reference Gómez-Torrecillas, Năstăsescu and Torrecillas9, Reference Positselski29, Reference Wang and Wu47]. A coalgebra
![]() $C$
is said to be left Artinian if it is Artinian as an object of the category of left
$C$
is said to be left Artinian if it is Artinian as an object of the category of left
![]() $C$
-comodules
$C$
-comodules
![]() $C{{-\mathsf{Comod}}}$
, that is, any descending chain of left coideals in
$C{{-\mathsf{Comod}}}$
, that is, any descending chain of left coideals in
![]() $C$
terminates [Reference Gómez-Torrecillas, Năstăsescu and Torrecillas9], [Reference Positselski29, Section 2]. (Here by a left coideal in
$C$
terminates [Reference Gómez-Torrecillas, Năstăsescu and Torrecillas9], [Reference Positselski29, Section 2]. (Here by a left coideal in
![]() $C$
one means a left subcomodule in the left
$C$
one means a left subcomodule in the left
![]() $C$
-comodule
$C$
-comodule
![]() $C$
.)
$C$
.)
Lemma 10.1. (a) A coalgebra
![]() $C$
is left Artinian if and only if it is left co-Noetherian and the maximal cosemisimple subcoalgebra of
$C$
is left Artinian if and only if it is left co-Noetherian and the maximal cosemisimple subcoalgebra of
![]() $C$
is finite-dimensional. In particular, a conilpotent coalgebra is left Artinian if and only if it is left co-Noetherian.
$C$
is finite-dimensional. In particular, a conilpotent coalgebra is left Artinian if and only if it is left co-Noetherian.
(b) A coalgebra
![]() $C$
is left Artinian if and only if its dual algebra
$C$
is left Artinian if and only if its dual algebra
![]() $C^*$
is right Noetherian.
$C^*$
is right Noetherian.
Proof. See [Reference Gómez-Torrecillas, Năstăsescu and Torrecillas9, Proposition 1.6 of the published version, or Proposition 2.5 of the arXiv version] or [Reference Positselski29, Lemmas 2.6 and 2.10(b), Example 2.7, and the general discussion in Section 3].
Proposition 10.2. Any left or right co-Noetherian conilpotent coalgebra is weakly finitely Koszul.
Proof.
The weak finite Koszulity property of a conilpotent coalgebra is left-right symmetric by Proposition 4.1; so it suffices to consider the case of a left co-Noetherian conilpotent coalgebra
![]() $C$
. Then it follows easily from the co-Noetherianity that every finitely cogenerated left
$C$
. Then it follows easily from the co-Noetherianity that every finitely cogenerated left
![]() $C$
-comodule
$C$
-comodule
![]() $L$
has a coresolution
$L$
has a coresolution
![]() $J^\bullet$
by finitely cogenerated cofree
$J^\bullet$
by finitely cogenerated cofree
![]() $C$
-comodules
$C$
-comodules
![]() $J^n$
,
$J^n$
,
![]() $n\ge 0$
. In particular, this applies to all finite-dimensional left
$n\ge 0$
. In particular, this applies to all finite-dimensional left
![]() $C$
-comodules
$C$
-comodules
![]() $L$
; so the left
$L$
; so the left
![]() $C$
-comodule
$C$
-comodule
![]() $k$
has such a coresolution
$k$
has such a coresolution
![]() $J^\bullet$
. It remains to compute the spaces
$J^\bullet$
. It remains to compute the spaces
![]() $\textrm {Ext}^n_C(k,k)$
as
$\textrm {Ext}^n_C(k,k)$
as
![]() $H^n(\textrm {Hom}_C(k,J^\bullet ))$
and notice that the vector space
$H^n(\textrm {Hom}_C(k,J^\bullet ))$
and notice that the vector space
![]() $\textrm {Hom}_C(k,J^n)={}_\gamma J^n$
is finite-dimensional for every
$\textrm {Hom}_C(k,J^n)={}_\gamma J^n$
is finite-dimensional for every
![]() $n\ge 0$
.
$n\ge 0$
.
A left
![]() $C$
-comodule is said to be finitely copresented if it can be obtained as the kernel of a morphism of cofree
$C$
-comodule is said to be finitely copresented if it can be obtained as the kernel of a morphism of cofree
![]() $C$
-comodules
$C$
-comodules
![]() $C\otimes _k V\longrightarrow C\otimes _k U$
with finite-dimensional vector spaces of cogenerators
$C\otimes _k V\longrightarrow C\otimes _k U$
with finite-dimensional vector spaces of cogenerators
![]() $V$
and
$V$
and
![]() $U$
. A coalgebra
$U$
. A coalgebra
![]() $C$
is said to be left cocoherent if every finitely cogenerated quotient comodule of a finitely copresented left
$C$
is said to be left cocoherent if every finitely cogenerated quotient comodule of a finitely copresented left
![]() $C$
-comodule is finitely copresented [Reference Positselski29, Section 2].
$C$
-comodule is finitely copresented [Reference Positselski29, Section 2].
Lemma 10.3.
Let
![]() $C$
be a conilpotent coalgebra over
$C$
be a conilpotent coalgebra over
![]() $k$
. Then
$k$
. Then
(a) a left
![]() $C$
-comodule
$C$
-comodule
![]() $L$
is finitely cogenerated if and only if the vector space
$L$
is finitely cogenerated if and only if the vector space
![]() $\textrm {Hom}_k(k,L)={}_\gamma L$
is finite-dimensional;
$\textrm {Hom}_k(k,L)={}_\gamma L$
is finite-dimensional;
(b) a finitely cogenerated left
![]() $C$
-comodule
$C$
-comodule
![]() $L$
is finitely copresented if and only if the vector space
$L$
is finitely copresented if and only if the vector space
![]() $\textrm {Ext}_C^1(k,L)$
is finite-dimensional;
$\textrm {Ext}_C^1(k,L)$
is finite-dimensional;
(c) in particular, the left
![]() $C$
-comodule
$C$
-comodule
![]() $k$
is finitely copresented if and only if the coalgebra
$k$
is finitely copresented if and only if the coalgebra
![]() $C$
is finitely cogenerated.
$C$
is finitely cogenerated.
Proof.
Part (a) follows from Lemma 3.5(a). To prove the “if” assertion in part (b), one can use Proposition 3.7(a) together with Corollary 3.6(a) to the effect that for any left
![]() $C$
-comodule
$C$
-comodule
![]() $L$
there exists a left exact sequence of left
$L$
there exists a left exact sequence of left
![]() $C$
-comodules
$C$
-comodules
![]() $0\longrightarrow L\longrightarrow C\otimes V_0\longrightarrow C\otimes _k V_1$
with
$0\longrightarrow L\longrightarrow C\otimes V_0\longrightarrow C\otimes _k V_1$
with
![]() $V_0\simeq \textrm {Hom}_C(k,L)$
and
$V_0\simeq \textrm {Hom}_C(k,L)$
and
![]() $V_1\simeq \textrm {Ext}_C^1(k,L)$
. The “only if” assertion in part (b) is deduced from the fact that the quotient comodule of a finitely cogenerated comodule by a finitely copresented subcomodule is finitely cogenerated; see [Reference Wang and Wu47, Theorem 6] or [Reference Positselski29, Lemma 2.8(a)]. In particular, the left
$V_1\simeq \textrm {Ext}_C^1(k,L)$
. The “only if” assertion in part (b) is deduced from the fact that the quotient comodule of a finitely cogenerated comodule by a finitely copresented subcomodule is finitely cogenerated; see [Reference Wang and Wu47, Theorem 6] or [Reference Positselski29, Lemma 2.8(a)]. In particular, the left
![]() $C$
-comodule
$C$
-comodule
![]() $k$
is finitely copresented if and only if the vector space
$k$
is finitely copresented if and only if the vector space
![]() $\textrm {Hom}_k(k,C/\gamma (k))= {}_\gamma (C/{}_\gamma C)=\textrm {Ext}^1_C(k,k)$
is finite-dimensional. This is part (c).
$\textrm {Hom}_k(k,C/\gamma (k))= {}_\gamma (C/{}_\gamma C)=\textrm {Ext}^1_C(k,k)$
is finite-dimensional. This is part (c).
Proposition 10.4. Any finitely cogenerated left or right cocoherent conilpotent coalgebra is weakly finitely Koszul.
Proof.
It suffices to consider the case when
![]() $C$
is left cocoherent. Then it follows from the cocoherence and the same fact that the quotient comodule of a finitely cogenerated comodule by a finitely copresented subcomodule is finitely cogenerated (mentioned in the proof of Lemma 10.3) that any finitely copresented left
$C$
is left cocoherent. Then it follows from the cocoherence and the same fact that the quotient comodule of a finitely cogenerated comodule by a finitely copresented subcomodule is finitely cogenerated (mentioned in the proof of Lemma 10.3) that any finitely copresented left
![]() $C$
-comodule
$C$
-comodule
![]() $L$
has a coresolution
$L$
has a coresolution
![]() $J^\bullet$
by finitely cogenerated cofree
$J^\bullet$
by finitely cogenerated cofree
![]() $C$
-comodules
$C$
-comodules
![]() $J^n$
,
$J^n$
,
![]() $n\ge 0$
. If
$n\ge 0$
. If
![]() $C$
is finitely cogenerated, then this applies to
$C$
is finitely cogenerated, then this applies to
![]() $L=k$
(by Lemma 10.3(c)); so the left
$L=k$
(by Lemma 10.3(c)); so the left
![]() $C$
-comodule
$C$
-comodule
![]() $k$
has such a coresolution
$k$
has such a coresolution
![]() $J^\bullet$
. The argument finishes exactly in the same way as the proof of Proposition 10.2.
$J^\bullet$
. The argument finishes exactly in the same way as the proof of Proposition 10.2.
Remark 10.5. A coalgebra version of the Morita equivalence theory was developed by Takeuchi [45]. The notions of co-Noetherianity and co-coherence for coalgebras are not Morita–Takeuchi invariant (neither is conilpotence, of course; while Artinianity of coalgebras is invariant under the Morita–Takeuchi equivalence).
The co-Noetherianity and cocoherence properties have Morita–Takeuchi invariant versions, which are called quasi-co-Noetherianity and quasi-cocoherence in [Reference Positselski33, Section 3], [Reference Positselski30, Sections 5.1–5.4]. (The former property was called “strict quasi-finiteness” in [Reference Gómez-Torrecillas, Năstăsescu and Torrecillas9 ].) The key definition, going back to Takeuchi [Reference Takeuchi45 ], is that of a ‘quasi-finite comodule’, called quasi-finitely cogenerated in the terminology of [Reference Positselski33, Reference Positselski30 ]. A left
![]() $C$
-comodule
$C$
-comodule
![]() $L$
is called quasi-finitely cogenerated if the vector space
$L$
is called quasi-finitely cogenerated if the vector space
![]() $\textrm {Hom}_C(K,L)$
is finite-dimensional for any finite-dimensional left
$\textrm {Hom}_C(K,L)$
is finite-dimensional for any finite-dimensional left
![]() $C$
-comodule
$C$
-comodule
![]() $K$
.
$K$
.
One can see from [Reference Positselski29, Lemma 2.2(e)] that over a coalgebra
![]() $C$
with finite-dimensional maximal cosemisimple subcoalgebra (in particular, over a conilpotent coalgebra
$C$
with finite-dimensional maximal cosemisimple subcoalgebra (in particular, over a conilpotent coalgebra
![]() $C$
) the classes of finitely cogenerated and quasi-finitely cogenerated comodules coincide. Consequently, a conilpotent coalgebra is quasi-co-Noetherian in the sense of [33, 30] if and only if it is co-Noetherian, and a conilpotent coalgebra is quasi-cocoherent in the the sense of [33, 30] if and only if it is cocoherent. That is why we were not concerned with the quasi-co-Noetherianity and quasi-cocoherence properties in this section, but only with the co-Noetherianity and cocoherence properties.
$C$
) the classes of finitely cogenerated and quasi-finitely cogenerated comodules coincide. Consequently, a conilpotent coalgebra is quasi-co-Noetherian in the sense of [33, 30] if and only if it is co-Noetherian, and a conilpotent coalgebra is quasi-cocoherent in the the sense of [33, 30] if and only if it is cocoherent. That is why we were not concerned with the quasi-co-Noetherianity and quasi-cocoherence properties in this section, but only with the co-Noetherianity and cocoherence properties.
11. Cocommutative conilpotent coalgebras
Let
![]() $V$
be a
$V$
be a
![]() $k$
-vector space. We refer to [Reference Positselski36, Sections 2.3 and 3.3] for an introductory discussion of the cofree conilpotent (tensor) coalgebra
$k$
-vector space. We refer to [Reference Positselski36, Sections 2.3 and 3.3] for an introductory discussion of the cofree conilpotent (tensor) coalgebra
cospanned by a vector space
![]() $V$
. The cofree conilpotent cocommutative (symmetric) coalgebra
$V$
. The cofree conilpotent cocommutative (symmetric) coalgebra
![]() $\textrm {Sym}(V)$
is defined as the subcoalgebra
$\textrm {Sym}(V)$
is defined as the subcoalgebra
where
![]() $\textrm {Sym}^n(V)\subset V^{\otimes n}$
is the vector subspace of all symmetric tensors in
$\textrm {Sym}^n(V)\subset V^{\otimes n}$
is the vector subspace of all symmetric tensors in
![]() $V^{\otimes n}$
. One can easily see that
$V^{\otimes n}$
. One can easily see that
![]() $\textrm {Sym}(V)$
is the maximal cocommutative subcoalgebra in
$\textrm {Sym}(V)$
is the maximal cocommutative subcoalgebra in
![]() $\textrm {Ten}(V)$
; in fact, for any cocommutative coalgebra
$\textrm {Ten}(V)$
; in fact, for any cocommutative coalgebra
![]() $C$
over
$C$
over
![]() $k$
and coalgebra homomorphism
$k$
and coalgebra homomorphism
![]() $f:\ C\longrightarrow \textrm {Ten}(V)$
, the image of
$f:\ C\longrightarrow \textrm {Ten}(V)$
, the image of
![]() $f$
is contained in
$f$
is contained in
![]() $\textrm {Sym}(V)$
.
$\textrm {Sym}(V)$
.
Let
![]() $C$
be a conilpotent coalgebra over
$C$
be a conilpotent coalgebra over
![]() $k$
. Assume that
$k$
. Assume that
![]() $C$
is finitely cogenerated; so the vector space
$C$
is finitely cogenerated; so the vector space
![]() $V=\textrm {Ext}^1_C(k,k)=\ker (C_+\to C_+\otimes _k C_+)$
is finite-dimensional. Choose a
$V=\textrm {Ext}^1_C(k,k)=\ker (C_+\to C_+\otimes _k C_+)$
is finite-dimensional. Choose a
![]() $k$
-linear projection
$k$
-linear projection
![]() $g:C_+\longrightarrow V$
onto the vector subspace
$g:C_+\longrightarrow V$
onto the vector subspace
![]() $V\subset C_+$
. Then, according to [Reference Positselski26, Lemma 5.2(a)], the map
$V\subset C_+$
. Then, according to [Reference Positselski26, Lemma 5.2(a)], the map
![]() $g$
extends uniquely to coalgebra homomorphism
$g$
extends uniquely to coalgebra homomorphism
![]() $f:\ C\longrightarrow \textrm {Ten}(V)$
. Moreover, by [Reference Positselski26, Lemma 5.2(b)], the map
$f:\ C\longrightarrow \textrm {Ten}(V)$
. Moreover, by [Reference Positselski26, Lemma 5.2(b)], the map
![]() $f$
is injective.
$f$
is injective.
Assume additionally that
![]() $C$
is cocommutative. Then, following the discussion above, the image of the map
$C$
is cocommutative. Then, following the discussion above, the image of the map
![]() $f$
is contained in the subcoalgebra
$f$
is contained in the subcoalgebra
![]() $\textrm {Sym}(V)\subset \textrm {Ten}(V)$
. Hence,
$\textrm {Sym}(V)\subset \textrm {Ten}(V)$
. Hence,
![]() $C$
is a subcoalgebra in
$C$
is a subcoalgebra in
![]() $\textrm {Sym}(V)$
.
$\textrm {Sym}(V)$
.
Choose a
![]() $k$
-vector space basis
$k$
-vector space basis
![]() $x_1^*$
, …,
$x_1^*$
, …,
![]() $x_m^*$
in the vector space
$x_m^*$
in the vector space
![]() $V$
. Then
$V$
. Then
![]() $x_1$
, …,
$x_1$
, …,
![]() $x_m$
is a basis in the dual vector space
$x_m$
is a basis in the dual vector space
![]() $V^*$
. The choice of such bases identifies the
$V^*$
. The choice of such bases identifies the
![]() $k$
-vector space dual
$k$
-vector space dual
![]() $k$
-algebra
$k$
-algebra
![]() $\textrm {Sym}(V)^*$
to the symmetric coalgebra
$\textrm {Sym}(V)^*$
to the symmetric coalgebra
![]() $\textrm {Sym}(V)$
with the algebra of formal power series in the variables
$\textrm {Sym}(V)$
with the algebra of formal power series in the variables
![]() $x_1$
, …,
$x_1$
, …,
![]() $x_m$
,
$x_m$
,
Accordingly, the
![]() $k$
-algebra
$k$
-algebra
![]() $C^*$
dual to
$C^*$
dual to
![]() $C$
is a quotient algebra of the algebra of formal power series by an ideal
$C$
is a quotient algebra of the algebra of formal power series by an ideal
![]() $J\subset k[[x_1,\dotsc, x_m]]$
,
$J\subset k[[x_1,\dotsc, x_m]]$
,
Denote by
![]() $s_1$
, …,
$s_1$
, …,
![]() $s_m\in C^*$
the images of the elements
$s_m\in C^*$
the images of the elements
![]() $x_1$
, …,
$x_1$
, …,
![]() $x_m$
under the surjective
$x_m$
under the surjective
![]() $k$
-algebra homomorphism
$k$
-algebra homomorphism
![]() $k[[x_1,\dotsc, x_m]]\longrightarrow C^*$
dual to the injective coalgebra map
$k[[x_1,\dotsc, x_m]]\longrightarrow C^*$
dual to the injective coalgebra map
![]() $C\longrightarrow \textrm {Sym}(V)$
. We have shown that
$C\longrightarrow \textrm {Sym}(V)$
. We have shown that
![]() $C^*$
is a complete Noetherian commutative local ring with the maximal ideal
$C^*$
is a complete Noetherian commutative local ring with the maximal ideal
![]() $I=(s_1,\dotsc, s_m)\subset C^*$
generated by the elements
$I=(s_1,\dotsc, s_m)\subset C^*$
generated by the elements
![]() $s_1$
, …,
$s_1$
, …,
![]() $s_m\in C^*$
. Indeed, the ring of formal power series
$s_m\in C^*$
. Indeed, the ring of formal power series
![]() $k[[x_1,\dotsc, x_m]]$
is a complete Noetherian commutative local ring; hence so is any (nonzero) quotient ring of
$k[[x_1,\dotsc, x_m]]$
is a complete Noetherian commutative local ring; hence so is any (nonzero) quotient ring of
![]() $k[[x_1,\dotsc, x_m]]$
.
$k[[x_1,\dotsc, x_m]]$
.
Corollary 11.1. All finitely cogenerated cocommutative conilpotent coalgebras are co-Noetherian. Consequently, all such coalgebras are weakly finitely Koszul.
Proof.
Let
![]() $C$
be a finitely cogenerated cocommutative conilpotent coalgebra over
$C$
be a finitely cogenerated cocommutative conilpotent coalgebra over
![]() $k$
. Then the algebra
$k$
. Then the algebra
![]() $C^*$
is Noetherian, as explained above. By Lemma 10.1(a–b), it follows that the coalgebra
$C^*$
is Noetherian, as explained above. By Lemma 10.1(a–b), it follows that the coalgebra
![]() $C$
is co-Noetherian. Now Proposition 10.2 tells us that
$C$
is co-Noetherian. Now Proposition 10.2 tells us that
![]() $C$
is weakly finitely Koszul.
$C$
is weakly finitely Koszul.
Corollary 11.1 says that the condition of Theorem1.2(vii) is satisfied for any finitely cogenerated cocommutative conilpotent coalgebra
![]() $C$
. Consequently, the triangulated functors
$C$
. Consequently, the triangulated functors
![]() $\Upsilon ^+:\ \mathsf{D}^+(C{{-\mathsf{Comod}}}) \longrightarrow \mathsf{D}^+(C^*{{-\mathsf{Mod}}})$
and
$\Upsilon ^+:\ \mathsf{D}^+(C{{-\mathsf{Comod}}}) \longrightarrow \mathsf{D}^+(C^*{{-\mathsf{Mod}}})$
and
![]() $\Theta ^-:\ \mathsf{D}^-(C{{-\mathsf{Contra}}})\longrightarrow \mathsf{D}^-(C^*{{-\mathsf{Mod}}})$
are fully faithful. In the rest of this section, our aim is to show, using the results of the paper [Reference Positselski25], that the triangulated functors
$\Theta ^-:\ \mathsf{D}^-(C{{-\mathsf{Contra}}})\longrightarrow \mathsf{D}^-(C^*{{-\mathsf{Mod}}})$
are fully faithful. In the rest of this section, our aim is to show, using the results of the paper [Reference Positselski25], that the triangulated functors
![]() $\Upsilon ^\varnothing :\ \mathsf{D}(C{{-\mathsf{Comod}}})\longrightarrow \mathsf{D}(C^*{{-\mathsf{Mod}}})$
and
$\Upsilon ^\varnothing :\ \mathsf{D}(C{{-\mathsf{Comod}}})\longrightarrow \mathsf{D}(C^*{{-\mathsf{Mod}}})$
and
![]() $\Theta ^\varnothing :\ \mathsf{D}(C{{-\mathsf{Contra}}})\longrightarrow \mathsf{D}(C^*{{-\mathsf{Mod}}})$
between the unbounded derived categories are actually fully faithful in this case, too.
$\Theta ^\varnothing :\ \mathsf{D}(C{{-\mathsf{Contra}}})\longrightarrow \mathsf{D}(C^*{{-\mathsf{Mod}}})$
between the unbounded derived categories are actually fully faithful in this case, too.
Let
![]() $R$
be a commutative ring and
$R$
be a commutative ring and
![]() $I\subset R$
be an ideal. An
$I\subset R$
be an ideal. An
![]() $R$
-module
$R$
-module
![]() $M$
is said to be
$M$
is said to be
![]() $I$
-torsion if for every pair of elements
$I$
-torsion if for every pair of elements
![]() $s\in I$
and
$s\in I$
and
![]() $x\in M$
there exists an integer
$x\in M$
there exists an integer
![]() $n\ge 1$
such that
$n\ge 1$
such that
![]() $s^nx=0$
in
$s^nx=0$
in
![]() $M$
. Equivalently,
$M$
. Equivalently,
![]() $M$
is
$M$
is
![]() $I$
-torsion if and only if for every
$I$
-torsion if and only if for every
![]() $s\in I$
one has
$s\in I$
one has
![]() $R[s^{-1}]\otimes _RM=0$
. Here,
$R[s^{-1}]\otimes _RM=0$
. Here,
![]() $R[s^{-1}]$
is the ring obtained by inverting formally the element
$R[s^{-1}]$
is the ring obtained by inverting formally the element
![]() $s\in R$
(or equivalently, by localizing
$s\in R$
(or equivalently, by localizing
![]() $R$
at the multiplicative subset
$R$
at the multiplicative subset
![]() $S=\{1,s,s^2,s^3,\dotsc \}\subset R$
spanned by
$S=\{1,s,s^2,s^3,\dotsc \}\subset R$
spanned by
![]() $s$
).
$s$
).
An
![]() $R$
-module
$R$
-module
![]() $P$
is said to be an
$P$
is said to be an
![]() $I$
-contramodule [Reference Positselski25, Reference Positselski27] if for every element
$I$
-contramodule [Reference Positselski25, Reference Positselski27] if for every element
![]() $s\in I$
one has
$s\in I$
one has
It is important to notice here that the projective dimension of the
![]() $R$
-module
$R$
-module
![]() $R[s^{-1}]$
can never exceed
$R[s^{-1}]$
can never exceed
![]() $1$
[Reference Positselski27, proof of Lemma3.1].
$1$
[Reference Positselski27, proof of Lemma3.1].
The full subcategory
![]() $R{{-\mathsf{Mod}}}_{I{{-\mathsf{tors}}}}$
of all
$R{{-\mathsf{Mod}}}_{I{{-\mathsf{tors}}}}$
of all
![]() $I$
-torsion
$I$
-torsion
![]() $R$
-modules is closed under submodules, quotients, extensions, and infinite direct sums in
$R$
-modules is closed under submodules, quotients, extensions, and infinite direct sums in
![]() $R{{-\mathsf{Mod}}}$
, as one can easily see [Reference Positselski27, Theorem 1.1(b)]. The full subcategory
$R{{-\mathsf{Mod}}}$
, as one can easily see [Reference Positselski27, Theorem 1.1(b)]. The full subcategory
![]() $R{{-\mathsf{Mod}}}_{I{{-\mathsf{ctra}}}}$
of all
$R{{-\mathsf{Mod}}}_{I{{-\mathsf{ctra}}}}$
of all
![]() $I$
-contramodule
$I$
-contramodule
![]() $R$
-modules is closed under kernels, cokernels, extensions, and infinite products in
$R$
-modules is closed under kernels, cokernels, extensions, and infinite products in
![]() $R{{-\mathsf{Mod}}}$
[Reference Geigle and Lenzing8, Proposition 1.1], [Reference Positselski27, Theorem 1.2(a)]. Consequently, both the categories
$R{{-\mathsf{Mod}}}$
[Reference Geigle and Lenzing8, Proposition 1.1], [Reference Positselski27, Theorem 1.2(a)]. Consequently, both the categories
![]() $R{{-\mathsf{Mod}}}_{I{{-\mathsf{tors}}}}$
and
$R{{-\mathsf{Mod}}}_{I{{-\mathsf{tors}}}}$
and
![]() $R{{-\mathsf{Mod}}}_{I{{-\mathsf{ctra}}}}$
are abelian, and the inclusion functors
$R{{-\mathsf{Mod}}}_{I{{-\mathsf{ctra}}}}$
are abelian, and the inclusion functors
![]() $R{{-\mathsf{Mod}}}_{I{{-\mathsf{tors}}}}\longrightarrow R{{-\mathsf{Mod}}}$
and
$R{{-\mathsf{Mod}}}_{I{{-\mathsf{tors}}}}\longrightarrow R{{-\mathsf{Mod}}}$
and
![]() $R{{-\mathsf{Mod}}}_{I{{-\mathsf{ctra}}}}\longrightarrow R{{-\mathsf{Mod}}}$
are exact.
$R{{-\mathsf{Mod}}}_{I{{-\mathsf{ctra}}}}\longrightarrow R{{-\mathsf{Mod}}}$
are exact.
Theorem 11.2.
Let
![]() $C$
be a finitely cogenerated cocommutative conilpotent coalgebra over a field
$C$
be a finitely cogenerated cocommutative conilpotent coalgebra over a field
![]() $k$
, and let
$k$
, and let
![]() $I\subset C^*$
be the maximal ideal of the complete Noetherian commutative local ring
$I\subset C^*$
be the maximal ideal of the complete Noetherian commutative local ring
![]() $C^*$
. Then
$C^*$
. Then
(a) the essential image of the comodule inclusion functor
![]() $\Upsilon :\ C{{-\mathsf{Comod}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
coincides with the full subcategory of
$\Upsilon :\ C{{-\mathsf{Comod}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
coincides with the full subcategory of
![]() $I$
-torsion
$I$
-torsion
![]() $C^*$
-modules
$C^*$
-modules
![]() $C^*{{-\mathsf{Mod}}}_{I{{-\mathsf{tors}}}}\subset C^*{{-\mathsf{Mod}}}$
, so the functor
$C^*{{-\mathsf{Mod}}}_{I{{-\mathsf{tors}}}}\subset C^*{{-\mathsf{Mod}}}$
, so the functor
![]() $\Upsilon$
induces a category equivalence
$\Upsilon$
induces a category equivalence
![]() $C{{-\mathsf{Comod}}}\simeq C^*{{-\mathsf{Mod}}}_{I{{-\mathsf{tors}}}}$
;
$C{{-\mathsf{Comod}}}\simeq C^*{{-\mathsf{Mod}}}_{I{{-\mathsf{tors}}}}$
;
(b) the contramodule forgetful functor
![]() $\Theta :\ C{{-\mathsf{Contra}}} \longrightarrow C^*{{-\mathsf{Mod}}}$
is fully faithful, and its essential image coincides with the full subcategory of
$\Theta :\ C{{-\mathsf{Contra}}} \longrightarrow C^*{{-\mathsf{Mod}}}$
is fully faithful, and its essential image coincides with the full subcategory of
![]() $I$
-contramodule
$I$
-contramodule
![]() $C^*$
-modules
$C^*$
-modules
![]() $C^*{{-\mathsf{Mod}}}_{I{{-\mathsf{ctra}}}}\subset C^*{{-\mathsf{Mod}}}$
, so the functor
$C^*{{-\mathsf{Mod}}}_{I{{-\mathsf{ctra}}}}\subset C^*{{-\mathsf{Mod}}}$
, so the functor
![]() $\Theta$
induces a category equivalence
$\Theta$
induces a category equivalence
![]() $C{{-\mathsf{Contra}}}\simeq C^*{{-\mathsf{Mod}}}_{I{{-\mathsf{ctra}}}}$
.
$C{{-\mathsf{Contra}}}\simeq C^*{{-\mathsf{Mod}}}_{I{{-\mathsf{ctra}}}}$
.
Proof.
The dual vector space
![]() $W^*$
to any (discrete infinite-dimensional) vector space
$W^*$
to any (discrete infinite-dimensional) vector space
![]() $W$
is naturally endowed with a pro-finite-dimensional (otherwise known as linearly compact or pseudocompact) topology. The annihilators of finite-dimensional vector subspaces in
$W$
is naturally endowed with a pro-finite-dimensional (otherwise known as linearly compact or pseudocompact) topology. The annihilators of finite-dimensional vector subspaces in
![]() $W$
are precisely all the open vector subspaces in
$W$
are precisely all the open vector subspaces in
![]() $W^*$
, and they form a base of neighborhoods of zero in
$W^*$
, and they form a base of neighborhoods of zero in
![]() $W^*$
. In the case of a coalgebra
$W^*$
. In the case of a coalgebra
![]() $C$
, the vector space
$C$
, the vector space
![]() $C^*$
with its pro-finite-dimensional topology is a topological algebra.
$C^*$
with its pro-finite-dimensional topology is a topological algebra.
A left
![]() $C^*$
-module
$C^*$
-module
![]() $N$
is said to be discrete (or “rational” in the terminology of [Reference Sweedler44]) if, for every element
$N$
is said to be discrete (or “rational” in the terminology of [Reference Sweedler44]) if, for every element
![]() $x\in N$
, the annihilator of
$x\in N$
, the annihilator of
![]() $x$
is an open left ideal in
$x$
is an open left ideal in
![]() $C^*$
. Equivalently, this means that the action map
$C^*$
. Equivalently, this means that the action map
![]() $C^*\times N\longrightarrow N$
is continuous in the pro-finite-dimensional topology on
$C^*\times N\longrightarrow N$
is continuous in the pro-finite-dimensional topology on
![]() $C^*$
and the discrete topology on
$C^*$
and the discrete topology on
![]() $N$
. The essential image of the comodule inclusion functor
$N$
. The essential image of the comodule inclusion functor
![]() $\Upsilon :\ C{{-\mathsf{Comod}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
consists precisely of all the discrete
$\Upsilon :\ C{{-\mathsf{Comod}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
consists precisely of all the discrete
![]() $C^*$
-modules [Reference Sweedler44, Propositions 2.1.1–2.1.2]. (Cf. the proof of Theorem1.2 in Section 9.) These assertions hold for any coalgebra
$C^*$
-modules [Reference Sweedler44, Propositions 2.1.1–2.1.2]. (Cf. the proof of Theorem1.2 in Section 9.) These assertions hold for any coalgebra
![]() $C$
over
$C$
over
![]() $k$
.
$k$
.
In the case of a finitely cogenerated cocommutative conilpotent coalgebra
![]() $C$
, the surjective map
$C$
, the surjective map
![]() $k[[x_1,\dotsc, x_m]]\longrightarrow C^*$
is open and continuous, because it is obtained by applying the dual vector space functor
$k[[x_1,\dotsc, x_m]]\longrightarrow C^*$
is open and continuous, because it is obtained by applying the dual vector space functor
![]() $W\longmapsto W^*=\textrm {Hom}_k(W,k)$
to the inclusion of discrete vector spaces (coalgebras)
$W\longmapsto W^*=\textrm {Hom}_k(W,k)$
to the inclusion of discrete vector spaces (coalgebras)
![]() $C\longrightarrow \textrm {Sym}(V)$
. The resulting pro-finite-dimensional topology on the algebra of formal power series
$C\longrightarrow \textrm {Sym}(V)$
. The resulting pro-finite-dimensional topology on the algebra of formal power series
![]() $k[[x_1,\dotsc, x_m]]$
is the usual (adic) topology of the formal power series. One easily concludes that a
$k[[x_1,\dotsc, x_m]]$
is the usual (adic) topology of the formal power series. One easily concludes that a
![]() $C^*$
-module is discrete if and only if it is discrete over
$C^*$
-module is discrete if and only if it is discrete over
![]() $k[[x_1,\dotsc, x_m]]$
. By the definition of the adic topology on a formal power series ring
$k[[x_1,\dotsc, x_m]]$
. By the definition of the adic topology on a formal power series ring
![]() $k[[x_1,\dotsc, x_m]]$
, a module over this ring is discrete if and only if it is a torsion module for the maximal ideal
$k[[x_1,\dotsc, x_m]]$
, a module over this ring is discrete if and only if it is a torsion module for the maximal ideal
![]() $(x_1,\dotsc, x_m)\subset k[[x_1,\dotsc, x_m]]$
. Hence, a
$(x_1,\dotsc, x_m)\subset k[[x_1,\dotsc, x_m]]$
. Hence, a
![]() $C^*$
-module
$C^*$
-module
![]() $N$
is discrete if and only if it is a torsion module for the ideal
$N$
is discrete if and only if it is a torsion module for the ideal
![]() $I=(s_1,\dotsc, s_m)\subset C^*$
. One can also observe that the pro-finite-dimensional topology on
$I=(s_1,\dotsc, s_m)\subset C^*$
. One can also observe that the pro-finite-dimensional topology on
![]() $C^*$
coincides with the
$C^*$
coincides with the
![]() $I$
-adic topology, since this holds for the coalgebra
$I$
-adic topology, since this holds for the coalgebra
![]() $\textrm {Sym}(V)$
. This proves part (a).
$\textrm {Sym}(V)$
. This proves part (a).
To prove part (b), one needs to use the concept of a contramodule over a topological ring as an intermediate step. Without going into the (somewhat involved) details of this definition, which can be found in [Reference Positselski22, Section 2.1], [Reference Positselski24, Section 2.1], or [Reference Positselski32, Sections 2.5–2.7], let us say that the category of left
![]() $C$
-contramodules is naturally equivalent (in fact, isomorphic) to the category of left contramodules over the topological ring
$C$
-contramodules is naturally equivalent (in fact, isomorphic) to the category of left contramodules over the topological ring
![]() $C^*$
. This equivalence agrees with the natural forgetful functors acting from the categories of left
$C^*$
. This equivalence agrees with the natural forgetful functors acting from the categories of left
![]() $C$
-contramodules and left
$C$
-contramodules and left
![]() $C^*$
-contramodules to the category of left
$C^*$
-contramodules to the category of left
![]() $C^*$
-modules. We refer to [Reference Positselski22, Section 1.10] or [Reference Positselski24, Section 2.3] for the details of the proof of this assertion.
$C^*$
-modules. We refer to [Reference Positselski22, Section 1.10] or [Reference Positselski24, Section 2.3] for the details of the proof of this assertion.
The contramodule forgetful functor
![]() $C{{-\mathsf{Contra}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
is fully faithful by Theorem7.4. In the special case of cocommutative coalgebras
$C{{-\mathsf{Contra}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
is fully faithful by Theorem7.4. In the special case of cocommutative coalgebras
![]() $C$
, one can also obtain this result as a particular case of the following theorems, which provide more information. By [Reference Positselski22, Theorem B.1.1] or [Reference Positselski24, Theorem 2.2], the forgetful functor from the category of
$C$
, one can also obtain this result as a particular case of the following theorems, which provide more information. By [Reference Positselski22, Theorem B.1.1] or [Reference Positselski24, Theorem 2.2], the forgetful functor from the category of
![]() $C^*$
-contramodules to the category of
$C^*$
-contramodules to the category of
![]() $C^*$
-modules is fully faithful, and its essential image is precisely the full subcategory of all
$C^*$
-modules is fully faithful, and its essential image is precisely the full subcategory of all
![]() $I$
-contramodule
$I$
-contramodule
![]() $C^*$
-modules. These results are actually applicable to any commutative Noetherian ring
$C^*$
-modules. These results are actually applicable to any commutative Noetherian ring
![]() $R$
with a fixed ideal
$R$
with a fixed ideal
![]() $I$
and the
$I$
and the
![]() $I$
-adic completion of
$I$
-adic completion of
![]() $R$
viewed as a topological ring with the
$R$
viewed as a topological ring with the
![]() $I$
-adic topology. (Morever, the Noetherianity condition can be weakened and replaced with a certain piece of the weak proregularity condition; see [Reference Positselski34, Proposition 1.5, Corollary 3.7, and Remark 3.8].) The combination of the references in this paragraph and in the previous one establishes part (b).
$I$
-adic topology. (Morever, the Noetherianity condition can be weakened and replaced with a certain piece of the weak proregularity condition; see [Reference Positselski34, Proposition 1.5, Corollary 3.7, and Remark 3.8].) The combination of the references in this paragraph and in the previous one establishes part (b).
Theorem 11.3.
Let
![]() $R$
be a commutative Noetherian ring and
$R$
be a commutative Noetherian ring and
![]() $I\subset R$
be an ideal. Then
$I\subset R$
be an ideal. Then
(a) the triangulated functor between the unbounded derived categories
induced by the inclusion of abelian categories
![]() $R{{-\mathsf{Mod}}}_{I{{-\mathsf{tors}}}}\longrightarrow R{{-\mathsf{Mod}}}$
is fully faithful;
$R{{-\mathsf{Mod}}}_{I{{-\mathsf{tors}}}}\longrightarrow R{{-\mathsf{Mod}}}$
is fully faithful;
(b) the triangulated functor between the unbounded derived categories
induced by the inclusion of abelian categories
![]() $R{{-\mathsf{Mod}}}_{I{{-\mathsf{ctra}}}}\longrightarrow R{{-\mathsf{Mod}}}$
is fully faithful.
$R{{-\mathsf{Mod}}}_{I{{-\mathsf{ctra}}}}\longrightarrow R{{-\mathsf{Mod}}}$
is fully faithful.
Proof.
These assertions actually hold for any weakly proregular finitely generated ideal
![]() $I$
in a (not necessarily Noetherian) commutative ring
$I$
in a (not necessarily Noetherian) commutative ring
![]() $R$
; while in a Noetherian commutative ring, any ideal is weakly proregular. See [Reference Positselski25, Theorems 1.3 and 2.9] for the details. The proofs are based on the observations that (the derived functors of) the right adjoint functor
$R$
; while in a Noetherian commutative ring, any ideal is weakly proregular. See [Reference Positselski25, Theorems 1.3 and 2.9] for the details. The proofs are based on the observations that (the derived functors of) the right adjoint functor
![]() $\Gamma :\ R{{-\mathsf{Mod}}}\longrightarrow R{{-\mathsf{Mod}}}_{I{{-\mathsf{tors}}}}$
and the left adjoint functor
$\Gamma :\ R{{-\mathsf{Mod}}}\longrightarrow R{{-\mathsf{Mod}}}_{I{{-\mathsf{tors}}}}$
and the left adjoint functor
![]() $\Delta :\ R{{-\mathsf{Mod}}}\longrightarrow R{{-\mathsf{Mod}}}_{I{{-\mathsf{ctra}}}}$
to the inclusions of abelian categories in question have finite homological dimensions, which go back to [Reference Porta, Shaul and Yekutieli18, Corollaries 4.28 and 5.27] and were also mentioned in [Reference Positselski25, Lemmas 1.2(b) and 2.7(b)]. See [Reference Positselski28, Theorem 6.4] (cf. [Reference Positselski31, Proposition 6.5]) for an abstract formulation.
$\Delta :\ R{{-\mathsf{Mod}}}\longrightarrow R{{-\mathsf{Mod}}}_{I{{-\mathsf{ctra}}}}$
to the inclusions of abelian categories in question have finite homological dimensions, which go back to [Reference Porta, Shaul and Yekutieli18, Corollaries 4.28 and 5.27] and were also mentioned in [Reference Positselski25, Lemmas 1.2(b) and 2.7(b)]. See [Reference Positselski28, Theorem 6.4] (cf. [Reference Positselski31, Proposition 6.5]) for an abstract formulation.
Corollary 11.4.
Let
![]() $C$
be a finitely cogenerated cocommutative conilpotent coalgebra over a field
$C$
be a finitely cogenerated cocommutative conilpotent coalgebra over a field
![]() $k$
. Then
$k$
. Then
(a) the triangulated functor between the unbounded derived categories
induced by the comodule inclusion functor
![]() $\Upsilon :\ C{{-\mathsf{Comod}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
is fully faithful;
$\Upsilon :\ C{{-\mathsf{Comod}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
is fully faithful;
(b) the triangulated functor between the unbounded derived categories
induced by the contramodule forgetful functor
![]() $C{{-\mathsf{Contra}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
is fully faithful.
$C{{-\mathsf{Contra}}}\longrightarrow C^*{{-\mathsf{Mod}}}$
is fully faithful.
Acknowledgement
I am grateful to Victor Roca i Lucio and Teresa Conde for stimulating correspondence. I also wish to thank Jan Št’ovíček for helpful conversations. An acknowledgement is due to an anonymous referee for the suggestion to include Remark 8.2. The author is supported by the GAČR project 23-05148S and the Czech Academy of Sciences (RVO 67985840).
Competing interests
The author declares none.
Appendix. Standard Category-Theoretic Observations
In this appendix we collect several elementary category-theoretic homological algebra lemmas, which are used in Sections 5–8. The following lemma tells how far one can go computing the Ext groups with a resolution which is only initially projective.
Lemma A.1.
Let
![]() $\mathsf{A}$
be an abelian category and
$\mathsf{A}$
be an abelian category and
![]() $0\longleftarrow X\longleftarrow P_0\longleftarrow P_1\longleftarrow P_2\longleftarrow \dotsb$
be an exact sequence in
$0\longleftarrow X\longleftarrow P_0\longleftarrow P_1\longleftarrow P_2\longleftarrow \dotsb$
be an exact sequence in
![]() $\mathsf{A}$
. Then for every object
$\mathsf{A}$
. Then for every object
![]() $Y\in \mathsf{A}$
there are natural maps of abelian groups
$Y\in \mathsf{A}$
there are natural maps of abelian groups
defined for all
![]() $n\ge 0$
. The map (47) is an isomorphism whenever the objects
$n\ge 0$
. The map (47) is an isomorphism whenever the objects
![]() $P_i$
are projective in
$P_i$
are projective in
![]() $\mathsf{A}$
for all
$\mathsf{A}$
for all
![]() $0\le i\le n-1$
.
$0\le i\le n-1$
.
Proof.
The point of the lemma is that one does not need the objects
![]() $P_n$
or
$P_n$
or
![]() $P_{n+1}$
(but only the objects
$P_{n+1}$
(but only the objects
![]() $P_0$
, …,
$P_0$
, …,
![]() $P_{n-1}$
) to be projective in order to compute
$P_{n-1}$
) to be projective in order to compute
![]() $\textrm {Ext}^n_{\mathsf{A}}(X,Y)$
using a resolution
$\textrm {Ext}^n_{\mathsf{A}}(X,Y)$
using a resolution
![]() $P_\bullet$
of an object
$P_\bullet$
of an object
![]() $X\in \mathsf{A}$
. The proof is standard. Denote by
$X\in \mathsf{A}$
. The proof is standard. Denote by
![]() $X_i$
the image of the differential
$X_i$
the image of the differential
![]() $P_i\longrightarrow P_{i-1}$
(so
$P_i\longrightarrow P_{i-1}$
(so
![]() $X=X_0$
). Then the connecting homomorphisms in the long exact sequences of groups
$X=X_0$
). Then the connecting homomorphisms in the long exact sequences of groups
![]() $\textrm {Ext}^*_{\mathsf{A}}({-},Y)$
related to the short exact sequences
$\textrm {Ext}^*_{\mathsf{A}}({-},Y)$
related to the short exact sequences
![]() $0\longrightarrow X_{i+1}\longrightarrow P_i\longrightarrow X_i\longrightarrow 0$
in
$0\longrightarrow X_{i+1}\longrightarrow P_i\longrightarrow X_i\longrightarrow 0$
in
![]() $\mathsf{A}$
provide natural maps of abelian groups
$\mathsf{A}$
provide natural maps of abelian groups
whose composition is the desired map (47). Furthermore, the map
![]() $H^n(\textrm {Hom}_{\mathsf{A}}(P_\bullet, Y))\longrightarrow \textrm {Ext}^1_{\mathsf{A}}(X_{n-1},Y)$
is an isomorphism whenever
$H^n(\textrm {Hom}_{\mathsf{A}}(P_\bullet, Y))\longrightarrow \textrm {Ext}^1_{\mathsf{A}}(X_{n-1},Y)$
is an isomorphism whenever
![]() $\textrm {Ext}^1_{\mathsf{A}}(P_{n-1},Y)=0$
; the map
$\textrm {Ext}^1_{\mathsf{A}}(P_{n-1},Y)=0$
; the map
![]() $\textrm {Ext}^1_{\mathsf{A}}(X_{n-1},Y)\longrightarrow \textrm {Ext}^2_{\mathsf{A}}(X_{n-2},Y)$
is an isomorphism whenever
$\textrm {Ext}^1_{\mathsf{A}}(X_{n-1},Y)\longrightarrow \textrm {Ext}^2_{\mathsf{A}}(X_{n-2},Y)$
is an isomorphism whenever
![]() $\textrm {Ext}^1_{\mathsf{A}}(P_{n-2},Y)=0=\textrm {Ext}^2_{\mathsf{A}}(P_{n-2},Y)$
, etc.; and the map
$\textrm {Ext}^1_{\mathsf{A}}(P_{n-2},Y)=0=\textrm {Ext}^2_{\mathsf{A}}(P_{n-2},Y)$
, etc.; and the map
![]() $\textrm {Ext}^{n-1}_{\mathsf{A}}(X_1,Y)\longrightarrow \textrm {Ext}^n_{\mathsf{A}}(X_0,Y)$
is an isomorphism whenever
$\textrm {Ext}^{n-1}_{\mathsf{A}}(X_1,Y)\longrightarrow \textrm {Ext}^n_{\mathsf{A}}(X_0,Y)$
is an isomorphism whenever
![]() $\textrm {Ext}^{n-1}_{\mathsf{A}}(P_0,Y)=0=\textrm {Ext}^n_{\mathsf{A}}(P_0,Y)$
.
$\textrm {Ext}^{n-1}_{\mathsf{A}}(P_0,Y)=0=\textrm {Ext}^n_{\mathsf{A}}(P_0,Y)$
.
The next lemma is a Tor version of Lemma A.1.
Lemma A.2.
Let
![]() $R$
be an associative ring and
$R$
be an associative ring and
![]() $0\longleftarrow X\longleftarrow F_0 \longleftarrow F_1\longleftarrow F_2\longleftarrow \dotsb$
be an exact sequence of right
$0\longleftarrow X\longleftarrow F_0 \longleftarrow F_1\longleftarrow F_2\longleftarrow \dotsb$
be an exact sequence of right
![]() $R$
-modules. Then for every left
$R$
-modules. Then for every left
![]() $R$
-module
$R$
-module
![]() $Y$
there are natural maps of abelian groups
$Y$
there are natural maps of abelian groups
defined for all
![]() $n\ge 0$
. The map (48) is an isomorphism whenever the
$n\ge 0$
. The map (48) is an isomorphism whenever the
![]() $R$
-modules
$R$
-modules
![]() $F_i$
are flat for all
$F_i$
are flat for all
![]() $0\le i\le n-1$
.
$0\le i\le n-1$
.
The following lemma is very easy.
Lemma A.3.
Let
![]() $\Phi :\ \mathsf{B}\longrightarrow \mathsf{A}$
be a fully faithful exact functor of abelian categories, and let
$\Phi :\ \mathsf{B}\longrightarrow \mathsf{A}$
be a fully faithful exact functor of abelian categories, and let
![]() $X$
,
$X$
,
![]() $Y\in \mathsf{B}$
be two objects. Then the map
$Y\in \mathsf{B}$
be two objects. Then the map
induced by the functor
![]() $\Phi$
is injective. This map is surjective if and only if, for any short exact sequence
$\Phi$
is injective. This map is surjective if and only if, for any short exact sequence
![]() $0\longrightarrow \Phi (Y)\longrightarrow A\longrightarrow \Phi (X)\longrightarrow 0$
in
$0\longrightarrow \Phi (Y)\longrightarrow A\longrightarrow \Phi (X)\longrightarrow 0$
in
![]() $\mathsf{A}$
, the object
$\mathsf{A}$
, the object
![]() $A$
belongs to the essential image of
$A$
belongs to the essential image of
![]() $\Phi$
.
$\Phi$
.
Proof. The proof is left to the reader.
The next lemma is essentially well-known, but we give it a more precise formulation than it usually receives.
Lemma A.4.
Let
![]() $\mathsf{A}$
and
$\mathsf{A}$
and
![]() $\mathsf{B}$
be abelian categories, and let
$\mathsf{B}$
be abelian categories, and let
![]() $\Phi :\ \mathsf{B}\longrightarrow \mathsf{A}$
be an exact functor. Let
$\Phi :\ \mathsf{B}\longrightarrow \mathsf{A}$
be an exact functor. Let
![]() $n\ge 1$
be an integer and
$n\ge 1$
be an integer and
![]() $Y\in \mathsf{B}$
be a fixed object.
$Y\in \mathsf{B}$
be a fixed object.
(a) Assume that the map of groups
![]() $\textrm {Ext}^{n-1}$
$\textrm {Ext}^{n-1}$
induced by the functor
![]() $\Phi$
is an isomorphism for all objects
$\Phi$
is an isomorphism for all objects
![]() $X\in \mathsf{B}$
. Then the map of groups
$X\in \mathsf{B}$
. Then the map of groups
![]() $\textrm {Ext}^n$
$\textrm {Ext}^n$
induced by the functor
![]() $\Phi$
is injective for all objects
$\Phi$
is injective for all objects
![]() $X\in \mathsf{B}$
.
$X\in \mathsf{B}$
.
(b) More generally, let
![]() $0\longrightarrow X\longrightarrow P\longrightarrow T \longrightarrow 0$
be a short exact sequence in
$0\longrightarrow X\longrightarrow P\longrightarrow T \longrightarrow 0$
be a short exact sequence in
![]() $\mathsf{B}$
. Assume that the map
$\mathsf{B}$
. Assume that the map
![]() $\textrm {Ext}^{n-1}_{\mathsf{B}}(P,Y)\longrightarrow \textrm {Ext}^{n-1}_{\mathsf{A}}(\Phi (P),\Phi (Y))$
is surjective, while the map
$\textrm {Ext}^{n-1}_{\mathsf{B}}(P,Y)\longrightarrow \textrm {Ext}^{n-1}_{\mathsf{A}}(\Phi (P),\Phi (Y))$
is surjective, while the map
![]() $\textrm {Ext}^{n-1}_{\mathsf{B}}(X,Y)\longrightarrow \textrm {Ext}^{n-1}_{\mathsf{A}}(\Phi (X),\Phi (Y))$
is injective. Then the intersection of the kernel of the map
$\textrm {Ext}^{n-1}_{\mathsf{B}}(X,Y)\longrightarrow \textrm {Ext}^{n-1}_{\mathsf{A}}(\Phi (X),\Phi (Y))$
is injective. Then the intersection of the kernel of the map
![]() $\textrm {Ext}^n_{\mathsf{B}}(T,Y)\longrightarrow \textrm {Ext}^n_{\mathsf{B}}(P,Y)$
induced by the epimorphism
$\textrm {Ext}^n_{\mathsf{B}}(T,Y)\longrightarrow \textrm {Ext}^n_{\mathsf{B}}(P,Y)$
induced by the epimorphism
![]() $P\longrightarrow T$
with the kernel of the map
$P\longrightarrow T$
with the kernel of the map
![]() $\textrm {Ext}^n_{\mathsf{B}}(T,Y)\longrightarrow \textrm {Ext}^n_{\mathsf{A}}(\Phi (T),\Phi (Y))$
induced by the functor
$\textrm {Ext}^n_{\mathsf{B}}(T,Y)\longrightarrow \textrm {Ext}^n_{\mathsf{A}}(\Phi (T),\Phi (Y))$
induced by the functor
![]() $\Phi$
is the zero subgroup in
$\Phi$
is the zero subgroup in
![]() $\textrm {Ext}^n_{\mathsf{B}}(T,Y)$
.
$\textrm {Ext}^n_{\mathsf{B}}(T,Y)$
.
Proof. This observation goes back, at least, to [Reference Beilinson, Bernstein, Deligne and Gabber2, Remarque 3.1.17(i)]. Part (b) is provable by a straightforward diagram chase of the commutative diagram of a morphism of long exact sequences
![]()
induced by the functor
![]() $\Phi$
.
$\Phi$
.
To deduce (a) from (b), let
![]() $T\in \mathsf{B}$
be an object and
$T\in \mathsf{B}$
be an object and
![]() $\beta \in \textrm {Ext}^n_{\mathsf{B}}(T,Y)$
be an extension class annihilated by the map
$\beta \in \textrm {Ext}^n_{\mathsf{B}}(T,Y)$
be an extension class annihilated by the map
![]() $\textrm {Ext}^n_{\mathsf{B}}(T,Y)\longrightarrow \textrm {Ext}^n_{\mathsf{A}}(\Phi (T),\Phi (Y))$
. Choose an epimorphism
$\textrm {Ext}^n_{\mathsf{B}}(T,Y)\longrightarrow \textrm {Ext}^n_{\mathsf{A}}(\Phi (T),\Phi (Y))$
. Choose an epimorphism
![]() $P\longrightarrow T$
in
$P\longrightarrow T$
in
![]() $\mathsf{B}$
such that
$\mathsf{B}$
such that
![]() $\beta$
is annihilated by the induced map
$\beta$
is annihilated by the induced map
![]() $\textrm {Ext}^n_{\mathsf{B}}(T,Y)\longrightarrow \textrm {Ext}^n_{\mathsf{B}}(P,Y)$
. Then part (b) implies that
$\textrm {Ext}^n_{\mathsf{B}}(T,Y)\longrightarrow \textrm {Ext}^n_{\mathsf{B}}(P,Y)$
. Then part (b) implies that
![]() $\beta =0$
.
$\beta =0$
.
The final series of lemmas concerns abelian categories with enough injective or projective objects.
Lemma A.5.
Let
![]() $\mathsf{A}$
and
$\mathsf{A}$
and
![]() $\mathsf{B}$
be abelian categories, and let
$\mathsf{B}$
be abelian categories, and let
![]() $\Phi :\ \mathsf{B}\longrightarrow \mathsf{A}$
be a fully faithful exact functor. Assume that there are enough injective objects in the abelian category
$\Phi :\ \mathsf{B}\longrightarrow \mathsf{A}$
be a fully faithful exact functor. Assume that there are enough injective objects in the abelian category
![]() $\mathsf{B}$
, and denote by
$\mathsf{B}$
, and denote by
![]() $\mathsf{B}_{\mathsf{inj}}\subset \mathsf{B}$
the class of all such injective objects. Let
$\mathsf{B}_{\mathsf{inj}}\subset \mathsf{B}$
the class of all such injective objects. Let
![]() $n\ge 1$
be an integer. Then the following two conditions are equivalent:
$n\ge 1$
be an integer. Then the following two conditions are equivalent:
-
(1) the map of Ext groups
induced by the functor \begin{equation*} \textrm {Ext}^i_{\mathsf{B}}(X,Y) \longrightarrow \textrm {Ext}^i_{\mathsf{A}}(\Phi (X),\Phi (Y)) \end{equation*}
\begin{equation*} \textrm {Ext}^i_{\mathsf{B}}(X,Y) \longrightarrow \textrm {Ext}^i_{\mathsf{A}}(\Phi (X),\Phi (Y)) \end{equation*}
 $\Phi$
is an isomorphism for all objects
$\Phi$
is an isomorphism for all objects
 $X$
,
$X$
,
 $Y\in \mathsf{B}$
and integers
$Y\in \mathsf{B}$
and integers
 $0\le i\le n$
;
$0\le i\le n$
;
-
(2)
 $\textrm {Ext}^i_{\mathsf{A}}(\Phi (X),\Phi (J))=0$
for all objects
$\textrm {Ext}^i_{\mathsf{A}}(\Phi (X),\Phi (J))=0$
for all objects
 $X\in \mathsf{B}$
and
$X\in \mathsf{B}$
and
 $J\in \mathsf{B}_{\mathsf{inj}}$
, and all
$J\in \mathsf{B}_{\mathsf{inj}}$
, and all
 $1\le i\le n$
.
$1\le i\le n$
.
Proof.
(1)
![]() $\Longrightarrow$
(2) Condition (2) is clearly the particular case of (1) for
$\Longrightarrow$
(2) Condition (2) is clearly the particular case of (1) for
![]() $Y=J\in \mathsf{B}_{\mathsf{inj}}$
.
$Y=J\in \mathsf{B}_{\mathsf{inj}}$
.
(2)
![]() $\Longrightarrow$
(1) For
$\Longrightarrow$
(1) For
![]() $i=0$
, the map of Ext groups in question is an isomorphism by the assumption that the functor
$i=0$
, the map of Ext groups in question is an isomorphism by the assumption that the functor
![]() $\Phi$
is fully faithful. For
$\Phi$
is fully faithful. For
![]() $1\le i\le n$
, we proceed by increasing induction on
$1\le i\le n$
, we proceed by increasing induction on
![]() $i$
.
$i$
.
Given an object
![]() $Y\in \mathsf{B}$
, choose a short exact sequence
$Y\in \mathsf{B}$
, choose a short exact sequence
![]() $0\longrightarrow Y\longrightarrow J\longrightarrow Y'\longrightarrow 0$
in
$0\longrightarrow Y\longrightarrow J\longrightarrow Y'\longrightarrow 0$
in
![]() $\mathsf{B}$
with
$\mathsf{B}$
with
![]() $J\in \mathsf{B}_{\mathsf{inj}}$
. Then the exact functor
$J\in \mathsf{B}_{\mathsf{inj}}$
. Then the exact functor
![]() $\Phi$
induces a commutative diagram of a morphism of long exact sequences
$\Phi$
induces a commutative diagram of a morphism of long exact sequences
![]()
Here
![]() $\textrm {Ext}^i_{\mathsf{B}}(X,J)=0$
since
$\textrm {Ext}^i_{\mathsf{B}}(X,J)=0$
since
![]() $i\ge 1$
and
$i\ge 1$
and
![]() $J\in \mathsf{B}_{\mathsf{inj}}$
, while
$J\in \mathsf{B}_{\mathsf{inj}}$
, while
![]() $\textrm {Ext}^i_{\mathsf{A}}(\Phi (X),\Phi (J))=0$
by (2). The leftmost and the middle vertical morphisms are isomorphisms by the induction assumption. It follows that the rightmost vertical morphism is an isomorphism, too (as desired).
$\textrm {Ext}^i_{\mathsf{A}}(\Phi (X),\Phi (J))=0$
by (2). The leftmost and the middle vertical morphisms are isomorphisms by the induction assumption. It follows that the rightmost vertical morphism is an isomorphism, too (as desired).
The following lemma is the dual version of Lemma A.5, but with a more precise claim.
Lemma A.6.
Let
![]() $\mathsf{A}$
and
$\mathsf{A}$
and
![]() $\mathsf{B}$
be abelian categories, and let
$\mathsf{B}$
be abelian categories, and let
![]() $\Phi :\ \mathsf{B}\longrightarrow \mathsf{A}$
be a fully faithful exact functor. Assume that there are enough projective objects in the abelian category
$\Phi :\ \mathsf{B}\longrightarrow \mathsf{A}$
be a fully faithful exact functor. Assume that there are enough projective objects in the abelian category
![]() $\mathsf{B}$
, and denote by
$\mathsf{B}$
, and denote by
![]() $\mathsf{B}_{\mathsf{proj}}\subset \mathsf{B}$
the class of all such projective objects. Let
$\mathsf{B}_{\mathsf{proj}}\subset \mathsf{B}$
the class of all such projective objects. Let
![]() $n\ge 1$
be an integer. Then, for any fixed object
$n\ge 1$
be an integer. Then, for any fixed object
![]() $Y\in \mathsf{B}$
, the following two conditions are equivalent:
$Y\in \mathsf{B}$
, the following two conditions are equivalent:
-
(1) the map of Ext groups
induced by the functor \begin{equation*} \textrm {Ext}^i_{\mathsf{B}}(X,Y) \longrightarrow \textrm {Ext}^i_{\mathsf{A}}(\Phi (X),\Phi (Y)) \end{equation*}
\begin{equation*} \textrm {Ext}^i_{\mathsf{B}}(X,Y) \longrightarrow \textrm {Ext}^i_{\mathsf{A}}(\Phi (X),\Phi (Y)) \end{equation*}
 $\Phi$
is an isomorphism for all objects
$\Phi$
is an isomorphism for all objects
 $X\in \mathsf{B}$
and integers
$X\in \mathsf{B}$
and integers
 $0\le i\le n$
;
$0\le i\le n$
;
-
(2)
 $\textrm {Ext}^i_{\mathsf{A}}(\Phi (P),\Phi (Y))=0$
for all objects
$\textrm {Ext}^i_{\mathsf{A}}(\Phi (P),\Phi (Y))=0$
for all objects
 $P\in \mathsf{B}_{\mathsf{proj}}$
and all
$P\in \mathsf{B}_{\mathsf{proj}}$
and all
 $1\le i\le n$
.
$1\le i\le n$
.
Proof.
Observe that the proof of Lemma A.5 works for a fixed object
![]() $X$
, and then dualize.
$X$
, and then dualize.
Our last lemma is the
![]() $n=0$
counterpart of Lemma A.6.
$n=0$
counterpart of Lemma A.6.
Lemma A.7.
Let
![]() $\mathsf{A}$
and
$\mathsf{A}$
and
![]() $\mathsf{B}$
be abelian categories, and let
$\mathsf{B}$
be abelian categories, and let
![]() $\Phi :\ \mathsf{B}\longrightarrow \mathsf{A}$
be an exact functor. Assume that there are enough projective objects in the abelian category
$\Phi :\ \mathsf{B}\longrightarrow \mathsf{A}$
be an exact functor. Assume that there are enough projective objects in the abelian category
![]() $\mathsf{B}$
, and denote by
$\mathsf{B}$
, and denote by
![]() $\mathsf{B}_{\mathsf{proj}}\subset \mathsf{B}$
the class of all such projective objects. Then, for any fixed object
$\mathsf{B}_{\mathsf{proj}}\subset \mathsf{B}$
the class of all such projective objects. Then, for any fixed object
![]() $Y\in \mathsf{B}$
, the following two conditions are equivalent:
$Y\in \mathsf{B}$
, the following two conditions are equivalent:
-
(1) the map of Hom groups
induced by the functor \begin{equation*} \textrm {Hom}_{\mathsf{B}}(X,Y) \longrightarrow \textrm {Hom}_{\mathsf{A}}(\Phi (X),\Phi (Y)) \end{equation*}
\begin{equation*} \textrm {Hom}_{\mathsf{B}}(X,Y) \longrightarrow \textrm {Hom}_{\mathsf{A}}(\Phi (X),\Phi (Y)) \end{equation*}
 $\Phi$
is an isomorphism for all objects
$\Phi$
is an isomorphism for all objects
 $X\in \mathsf{B}$
;
$X\in \mathsf{B}$
;
-
(2) the map of Hom groups
induced by the functor \begin{equation*} \textrm {Hom}_{\mathsf{B}}(P,Y) \longrightarrow \textrm {Hom}_{\mathsf{A}}(\Phi (P),\Phi (Y)) \end{equation*}
\begin{equation*} \textrm {Hom}_{\mathsf{B}}(P,Y) \longrightarrow \textrm {Hom}_{\mathsf{A}}(\Phi (P),\Phi (Y)) \end{equation*}
 $\Phi$
is an isomorphism for all objects
$\Phi$
is an isomorphism for all objects
 $P\in \mathsf{B}_{\mathsf{proj}}$
.
$P\in \mathsf{B}_{\mathsf{proj}}$
.
Proof.
Represent the object
![]() $X$
as the cokernel of a morphism of projective objects in the category
$X$
as the cokernel of a morphism of projective objects in the category
![]() $\mathsf{B}$
.
$\mathsf{B}$
.