No CrossRef data available.
Article contents
ON SOME QUESTIONS OF PARTITIO NUMERORUM: TRES CUBI
Published online by Cambridge University Press: 21 April 2020
Abstract
This paper is concerned with the function r3(n), the number of representations of n as the sum of at most three positive cubes, , Our understanding of this function is surprisingly poor, and we examine various averages of it. In particular 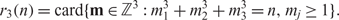 $$r_3(n) = {\mathrm{card}}\{\mathbf m\in\mathbb Z^3: m_1^3+m_2^3+m_3^3=n, m_j\ge1\}.$$ and
$$r_3(n) = {\mathrm{card}}\{\mathbf m\in\mathbb Z^3: m_1^3+m_2^3+m_3^3=n, m_j\ge1\}.$$ and 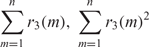 $${\sum_{m=1}^nr_3(m),\,\sum_{m=1}^nr_3(m)^2}$$
$${\sum_{m=1}^nr_3(m),\,\sum_{m=1}^nr_3(m)^2}$$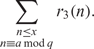 $${\sum_{\substack{ n\le x\\ n\equiv a\,\mathrm{mod}\,q }} r_3(n).\}$$
$${\sum_{\substack{ n\le x\\ n\equiv a\,\mathrm{mod}\,q }} r_3(n).\}$$
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2020. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust
Footnotes
In Memoriam Christopher Hooley FRS, 1928–2018
References
REFERENCES
Ayoub, R., A mean value theorem for quadratic fields, Pacific J. Math. 8 (1958), 23–27.Google Scholar
Boklan, K. D., A reduction technique in Waring’s problem, I, Acta Arithmetica 65 (1993), 147–161.Google Scholar
Boklan, K. D., The asymptotic formula in Waring’s problem, Mathematika 41 (1994), 329–347.CrossRefGoogle Scholar
Brüdern, J. and Wooley, T. D., The asymptotic formulae in Waring’s problem for cubes, J. für die reine und angewandte Mathematik 647 (2010), 1–23.Google Scholar
Cramér, H., Über das Teilerproblem von Piltz, Arkiv för Mat. Astr. och. Fysik 16 (1922), 155–157.Google Scholar
Erdös, P. and Fuchs, W. H. J., On a problem of additive number theory, J. London Math. Soc. 31 (1956), 67–73.CrossRefGoogle Scholar
Graham, S. W. and Kolesnik, G., Van Der Corput’s method of exponential sums, London Mathematical Society Lecture Note, vol. 126 (Cambridge University Press, 1991).Google Scholar
Hall, R. and Tenenbaum, G., Divisors (Cambridge University Press, London, 1988).CrossRefGoogle Scholar
Hardy, G. H.
, The average order of the functions P(x) and Δ(x), Proc. London Math. Soc. 15 (1923), 192–213.Google Scholar
Hardy, G. H. and Littlewood, J. E., Some problems of ‘partito numerorum’; III: On the expression of a number as a sum of primes, Acta Mathematica 44 (1923), 1–70.CrossRefGoogle Scholar
Hayashi, E. K., An elementary method for estimating error terms in additive number theory, Proc. Amer. Math Soc. 52 (1975), 55–59.CrossRefGoogle Scholar
Heath-Brown, D. R., Mean values of the zeta-function and divisor problems, in Recent Progress in Analytic Number Theory, Durham Symposium 1979, vol. 1 (Academic Press, London, 1981), 115–119.Google Scholar
Hooley, C., On the numbers that are representable as the sum of two cubes, J. Reine Angew. Math. 314 (1980), 146–173.Google Scholar
Hooley, C., On Waring’s problem for two squares and three cubes, J. für die reine und angewandte Mathemtik 328 (1981), 161–207.Google Scholar
Hooley, C., On some topics connected with Waring’s problem, J. für die reine und angewandte Mathematik 369 (1986), 110–153.Google Scholar
Hooley, C., On hypothesis K* in warings problem, in Sieve methods, exponential sums, and their applications in number theory (Greaves, G., Harman, G. and Huxley, M. N., Editors) (Cambridge University Press, 1996), 175–185.Google Scholar
Montgomery, H. L. and Vaughan, R. C., On the Erdös-Fuchs theorems, in A tribute to Paul Erdös (Baker, A., Bollobás, B. and Hajnal, A., Editors) (Cambridge University Press, 1990).Google Scholar
Quarel, D., On a numerical upper bound for the extended Goldbach conjecture, arXiv: 1801.01813 [math.HO]Google Scholar
Vaughan, R. C., On the addition of sequences of integers, J. Number Theory 4 (1972), 1–16.CrossRefGoogle Scholar
Vaughan, R. C., On Waring’s problem for cubes, J. für die reine und angewandte Mathemtik 365 (1986), 122–170.Google Scholar
Vaughan, R. C., On Waring’s problem for smaller exponents, Mathematika 33 (1986), 6–22.CrossRefGoogle Scholar
Vaughan, R. C., A mean value theorem for cubic fields, J. Number Theory 100 (2003), 169–183.CrossRefGoogle Scholar

