No CrossRef data available.
Article contents
An extension of a theorem of Gordon
Published online by Cambridge University Press: 18 May 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
In what follows all small Latin letters denote non-negative integers or functions whose values are non-negative integers. Let N = (n1, …, nj) be a j-dimensional vector and let q = q (k; N) = q(k; n1, …, nj) be the number of partitions of N into just k parts, each part being a vector whose components are non-negative integers. We write

for the generating function of q. We have
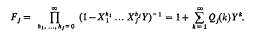 .
.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1965
References
REFERENCES
1.Carlitz, L., The expansion of certain products, Proc. American Math. Soc. 7 (1956), 558–564.CrossRefGoogle Scholar
2.Gordon, B., Two theorems on multipartite partitions, J. London Math. Soc. 38 (1963), 459–464.CrossRefGoogle Scholar
4.Wright, E. M., Partitions of multipartite numbers, Proc. American Math. Soc. 7 (1956), 880–890.CrossRefGoogle Scholar
5.Wright, E. M., Partitions of multipartite numbers into a fixed number of parts, Proc. London Math. Soc. (3) 11 (1961), 499–510.CrossRefGoogle Scholar
6.Wright, E. M., Direct proof of the basic theorem on multipartite partitions, Proc. American Math. Soc. 15 (1964), 469–472.CrossRefGoogle Scholar
7.Wright, E. M., Partition of multipartite numbers into k parts, J. für. Math. 216 (1964), 101–112.Google Scholar

