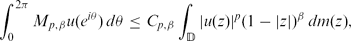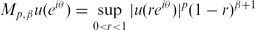Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Riihentaus, Juhani
2009.
Subharmonic functions, generalizations, weighted boundary behavior, and separately subharmonic functions: A survey.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 71,
Issue. 12,
p.
e2613.


 , there holds the inequality
, there holds the inequality