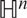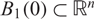Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Carriao, Paulo Cesar
Costa, Augusto Cesar dos Reis
Miyagaki, Olimpio Hiroshi
and
Vicente, Andre
2022.
Kirchhoff-type problems with critical Sobolev exponent in a hyperbolic space.
Electronic Journal of Differential Equations,
Vol. 2021,
Issue. 01-104,
p.
3.
Carrião, Paulo C.
Miyagaki, Olímpio H.
and
Vicente, André
2022.
Normalized solutions of Kirchhoff equations with critical and subcritical nonlinearities: the defocusing case.
Partial Differential Equations and Applications,
Vol. 3,
Issue. 5,
Carrião, Paulo Cesar
Miyagaki, Olímpio Hiroshi
and
Vicente, André
2023.
Exponential decay for semilinear wave equation with localized damping in the hyperbolic space.
Mathematische Nachrichten,
Vol. 296,
Issue. 1,
p.
130.
Carrião, Paulo Cesar
and
Vicente, André
2025.
Stability for the wave equation on hyperbolic space with acoustic boundary conditions.
Zeitschrift für angewandte Mathematik und Physik,
Vol. 76,
Issue. 2,
Alves, Claudianor O.
and
Shen, Liejun
2025.
On the existence of positive solutions to some classes of elliptic problems in Hyperbolic space.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
p.
1.