Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Patterson, S. J.
1986.
Tori in metaplectic covers of GL2 and applications to a formula of Loxton–Matthews.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 100,
Issue. 2,
p.
249.


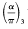 be that third root of unity so that
be that third root of unity so that